Д. ПОЙА

Математика

и правдоподобные рассуждения

Перевод с английского И. А. ВАЙНШТЕЙНА

Под редакцией С. А. ЯНОВСКОЙ

ИЗДАНИЕ ВТОРОЕ, ИСПРАВЛЕННОЕ

ИЗДАТЕЛЬСТВО «НАУКА»

ГЛАВНАЯ РЕДАКЦИЯ ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ

Москва 1975

Данная книга обращена прежде всего к тем, кто изучает математику, — начиная от учащихся старших классов и студентов и кончая специалистами в различных областях, которым приходится встречаться с применением математических методов исследования. Читатель узнает, какими путями добываются новые факты в математике, с какой степенью доверия следует относиться к той или иной математической гипотезе — одним словом, перед ним раскрывается подлинный процесс математического творчества. (Автор особенно подчеркивает общность путей открытия истин для всех естественных наук.) Благодаря этому книга является также незаменимым пособием для преподавателей математики всех ступеней. Увлекательность изложения, обилие исторических иллюстраций, а также предпринятая автором попытка построения теории правдоподобных (индуктивных) умозаключений делают книгу интересной и для профессионала-математика.

ОГЛАВЛЕНИЕ

Предисловие редактора перевода 9

Предисловие 14

Советы читателю 21

Том I

ИНДУКЦИЯ И АНАЛОГИЯ В МАТЕМАТИКЕ

Глава I. Индукция 25

1. Опыт и представление 25

2. Наводящие контакты 26

3. Подкрепляющие контакты 28

4. Индуктивный подход 30

Примеры и примечания к главе I 31

[12. Да и нет. 13. Опыт и поведение. 14. Логик, математик, физик и инженер.]

Глава II. Обобщение, специализация, аналогия 34

1. Обобщение, специализация, аналогия и индукция 34

2. Обобщение 34

3. Специализация 35

4. Аналогия 35

5. Обобщение, специализация и аналогия 37

6. Открытие по аналогии 39

7. Аналогия и индукция 43

Примеры и примечания к главе II 45

Первая часть 45

[1. Правильное обобщение. 5. Крайний частный случай. 7. Ведущий частный случай. 10. Частный случай-представитель. 11. Аналогичный случай. I8. Великие аналогии. 19 Выясненные аналогии. 20. Цитаты.]

Вторая часть 51

[21. Предположение Э. 44. Возражение и первый шаг к доказательству. 45. Второй шаг к доказательству. 46. Опасности аналогии.]

Глава III. Индукция в пространственной геометрии 56

1. Многогранники 56

2. Первые подкрепляющие контакты 58

3. Еще подкрепляющие контакты 59

4. Суровое испытание 60

5. Подтверждения и подтверждения 62

6. Совсем не похожий случай 63

7. Аналогия 63

8. Разбиение пространства 65

9. Видоизменение задачи 66

10. Обобщение, специализация, аналогия 66

11. Одна аналогичная задача 67

4[1]

12. Серия аналогичных задач 68

13. Много задач иногда легче решить, чем только одну 69

14. Предположение 69

15. Предсказание и подтверждение 70

16. Снова и лучше 71

17. Индукция подсказывает дедукцию; частный случай подсказывает общее доказательство 72

18. Еще предположения 73

Примеры и примечания к главе III 74

[21. Индукция: приспособление ума, приспособление языка. 31. Работа Декарта о многогранниках. 36. Дополнительные телесные углы, дополнительные сферические многоугольники.]

Глава IV. Индукция в теории чисел 80

1. Целочисленные прямоугольные треугольники 80

2. Суммы квадратов 83

3. О сумме четырех нечетных квадратов 84

4. Исследование примера 85

5. Составление таблицы наблюдений 86

6. Каково правило? 86

7. Природа индуктивного открытия 89

8. О природе индуктивных доводов 90

Примеры и примечания к главе IV 92

[1. Обозначения. 26. Опасности индукции.]

Глава V. Разные примеры индукции 97

1. Разложения 97

2. Приближения 99

3. Пределы 101

4. Попытка опровергнуть 101

5. Попытка доказать 103

6. Роль индуктивной фазы 105

Примеры и примечания к главе V 106

[15. Объясните наблюдаемые закономерности. 16. Классифицируйте наблюдаемые факты. 18. В чем различие?]

Глава VI. Одно более общее утверждение 111

1. Эйлер 111

2. Мемуар Эйлера 111

3. Переход к более общей точке зрения 120

4. Схематический очерк мемуара Эйлера 121

Примеры и примечания к главе VI 122

[1. Производящие функции. 7. Одна комбинаторная задача плоской геометрии. 10. Суммы квадратов. 19. Другая рекуррентная формула. 20. Другой Наиболее Необычайный Закон Чисел, Относящийся к Суммам их Делителей. 24. Как Эйлер упустил открытие. 25. Обобщение теоремы Эйлера о σ(n)]

Глава VII. Математическая индукция 128

1. Индуктивная фаза 128

2. Фаза доказательства 130

3. Исследование переходов 130

4. Техника математической индукции 132

Примеры и примечания к главе VII 137

[12. Доказать больше иногда легче. 14. Уравновесьте вашу теорему! 15. Перспектива. 17. Равны ли любые n чисел!]

5

Глава VIII. Максимумы и минимумы 141

1. Схемы 141

2. Пример 142

3. Схема касательной линии уровня 144

4. Примеры 146

5. Схема частного изменения 148

6. Теорема о среднем арифметическом и среднем геометрическом и ее первые следствия 150

Примеры и примечания к главе VIII 152

Первая часть 152

[1. Наименьшие и наибольшие расстояния в плоской геометрии. 2. Наименьшие и наибольшие расстояния в пространственной геометрии. 3. Линии уровня на плоскости. 4. Поверхности уровня в пространстве. 11. Принцип пересекающей линии уровня. 22. Принцип частного изменения. 23. Существование экстремума. 24. Видоизменение схемы частного изменения: бесконечный процесс. 25. Другое видоизменение схемы частного изменения: конечный процесс. 26. Графическое сравнение.]

Вторая часть 157

[33. Многоугольники и многогранники. Площадь и периметр. Объем и поверхность. 34. Прямая призма с квадратным основанием. 35. Прямой цилиндр. 36. Произвольная прямая призма. 37. Прямая. двойная пирамида с квадратным основанием. 38. Прямой двойной конус. 39. Произвольная прямая двойная пирамида. 43. Приложение геометрии к алгебре. 45. Приложение алгебры к геометрии. 51. Прямая пирамида с квадратным основанием. 52. Прямой конус. 53. Произвольная прямая пирамида. 55. Ящик без крышки. 56. Корыто. 57. Обломок. 62. Почтовая задача. 63. Задача Кеплера.]

Глава IX. Физическая математика 161

1. Оптическая интерпретация 161

2. Механическая интерпретация 165

3. Новая интерпретация 167

4. Открытие брахистохроны Иоганном Бернулли 171

5. Открытие Архимедом интегрального исчисления 173

Примеры и примечания к главе IX 177

[3. Треугольник с минимальным периметром, вписанный в данный треугольник. 9. Транспортный центр четырех точек в пространстве. 10. Транспортный центр четырех точек на плоскости. 11. Транспортная сеть для четырех точек. 12. Разверните и выпрямите. 13. Бильярд. 14. Геофизическое исследование. 23. Кратчайшие линии на многогранной поверхности. 24. Кратчайшие (геодезические) линии на кривой поверхности. 26. Построение посредством сгибания бумаги. 27. Бросается кость. 28. Всемирный потоп. 29. Не слишком глубоко. 30. Полезный крайний случай. 32. Вариационное исчисление. 33. От равновесия поперечных сечений к равновесию тел. 38. Ретроспективный взгляд на Метод Архимеда.]

Глава X. Изопериметрическая задача 185

1. Индуктивные доводы Декарта 185

2. Скрытые доводы 186

3. Физические доводы 187

4. Индуктивные доводы лорда Рэлея 187

5. Выведение следствий 188

6. Подтверждение следствий 191

7. Очень близко 195

8. Три формы изопериметрической теоремы 196

9. Приложения и вопросы 198

Примеры и примечания к главе Х 199

Первая часть 199

6

[1. Взгляд назад. 1. Могли бы вы вывести какую-либо часть этого результата иначе? 3. Заново с большими подробностями. 7. Можете ли вы воспользоваться этим методом для решения какой-нибудь другой задачи? 8. Более сильная форма изопериметрической теоремы.]

Вторая часть. 200

[16. Палка и веревка. 21. Две палки и две веревки. 25. Задача Дидоны в пространственной геометрии. 27. Биссекторы плоской области. 34. Биссекторы замкнутой поверхности. 40. Фигура многих совершенств. 41. Аналогичный случай 42. Правильные многогранники. 43. Индуктивные доводы.]

Глава XI. Другие виды правдоподобных доводов 206

1. Предположения и предположения 206

2. Суждение по родственному случаю 206

3. Суждение по общему случаю 208

4. Более простое предположение предпочтительнее 210

5. Фон 212

6. Неисчерпаем 215

7. Обычные эвристические допущения 216

Примеры и примечания к главе XI 217

[16. Общий случай. 19. Никакая идея не является действительно плохой. 20. Несколько обычных эвристических допущений. 21. Вознагражденный оптимизм. 23. Числовые выкладки и инженер.]

Заключительное замечание к первому тому 224

Том II

СХЕМЫ ПРАВДОПОДОБНЫХ УМОЗАКЛЮЧЕНИЙ

Предисловие ко II тому 227

Глава XII. Несколько бросающихся в глаза схем 229

1. Подтверждение следствия 229

2. Последовательное подтверждение нескольких следствий 231

3. Подтверждение невероятного следствия 233

4. Умозаключение по аналогии 236

5. Углубление аналогии 237

6. Затушеванное умозаключение по аналогии 239

Примеры и примечания к главе XII 240

[14. Индуктивное умозаключение по бесплодным усилиям.]

Глава XIII. Дальнейшие схемы и первые связи между схемами 244

1. Исследование следствия 244

2. Исследование возможного основания 245

3. Исследование противоречащего предположения 246

4. Логические термины 246

5. Логические связи между схемами правдоподобных умозаключений 250

6. Затушеванное умозаключение 251

7. Таблица 253

8. Комбинация простых схем 253

9. Об умозаключении по аналогии 254

10. Уточненное умозаключение 255

11. О последовательных подтверждениях 258

12. О соперничающих предположениях 258

13. О судебном доказательстве 260

Примеры и примечания к главе XIII 266

Первая часть 266

7

[9. Об индуктивном исследовании в математике и в физических науках. 10. Пробные общие формулировки.]

Вторая часть 271

[11. Более личное, более сложное. 12. Существует прямая, соединяющая две данные точки. 13. Существует прямая, проходящая через данную точку в данном направлении. Проведение параллели. 14. Наиболее очевидный случай может оказаться единственным возможным случаем. 15. Установление моды. Сила слов. 16. Это слишком невероятно, чтобы быть всего лишь совпадением. 17. Совершенствование аналогии. 18. Новое предположение. 19. Еще одпо новое предположение. 20. Что типично?]

Глава XIV. Случай. Неизменное соперничающее предположение 281

1. Случайные массовые явления 281

2. Понятие вероятности 283

3. Применение мешка и шаров 287

4. Исчисление вероятностей. Статистические гипотезы 290

5. Непосредственное предсказание частот 292

6. Объяснение явлений 298

7. Оценка статистических гипотез 301

8. Выбор между статистическими гипотезами 306

9. Оценка нестатистических предположений 313

10. Оценка математических предположений 326

Примеры и примечания к главе XIV 329

Первая часть 329

Вторая часть 330

[19. О понятии вероятности. 20. Как не следует истолковывать понятие вероятности, основанное на частоте. 24. Вероятность и решение задач. 25. Правильный и неправильный. 26. Фундаментальные правила исчисления вероятностей. 27. Независимость. 30. Перестановки и вероятность. 31. Сочетания и вероятность. 32. Выбор соперничающего статистического предположения. Пример. 33. Выбор соперничающего статистического предположения. Общие замечания.]

Глава XV. Исчисление вероятностей и логика правдоподобных рассуждений 338

1. Правила правдоподобных рассуждений 338

2. Один аспект доказательного рассуждения 341

3. Соответствующий аспект правдоподобного рассуждения 342

4. Один аспект исчисления вероятностей. Трудности 346

5. Один аспект исчисления вероятностей. Попытка 348

6. Исследование следствия 349

7. Исследование возможного основания 353

8. Исследование противоречащего предположения 354

9. Исследование одного за другим нескольких следствий 355

10. О косвенных уликах 358

Примеры и примечания к главе XV 359

[4. Вероятность и правдоподобность. 5. Правдоподобие и правдоподобность. 6. Попытка Лапласа связать индукцию с вероятностью. 7. Почему не количественно? 8. Бесконечно малые правдоподобности? 9. Правила допустимости.]

Глава XVI. Правдоподобные рассуждения в изобретении и обучении 371

1. Предмет настоящей главы 371

2. Рассказ о маленьком открытии 371

3. Процесс решения 374

4. Deus ex machina 375

5. Эвристическое оправдание 377

6. Рассказ о другом открытии 378

8

7. Несколько типичных указаний 382

8. Индукция в изобретении 383

9. Несколько слов преподавателю 388

Примеры и примечания к главе XVI 391

[1. Преподавателю: некоторые типы задач. 7. Qui himium probat, nihil probat. 8. Близость и правдоподобность. 9. Вычисления и правдоподобные рассуждения. 13. Формальное доказательство и правдоподобные рассуждения.]

Решения 398

Глава I (398). Глава II (399). Глава III (405). Глава IV (410). Глава V (414). Глава VI (417). Глава VII (420). Глава VIII (423). Глава IX (434). Глава X (440). Глава XI (446). Глава XII (450). Глава XIII (452). Глава XIV (455). Глава XV (460). Глава XVI (461)

Библиография 463

ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА

В применении к такой строгой науке, как математика, имеют ли смысл индукция (конечно, неполная), аналогия, наблюдение, гипотеза, эксперимент, короче говоря, методы, которыми пользуется каждый естествоиспытатель?

Ответу на этот вопрос посвящена книга известного математика и замечательного педагога Д. Пойа.

Советскому читателю, интересующемуся математикой, автор хорошо известен по книге Г. Полиа[2] и Г. Сеге. Задачи и теоремы из анализа, ч. I и II, второе издание которой вышло у нас в 1956 г. Уже в этой книге авторы ставили перед собой задачу указать начинающему математику пути к математическому творчеству, научить его способам, позволяющим лучше разбираться в трудных математических вопросах, открывать математические теоремы, решать задачи. Впоследствии Пойа написал на ту же тему популярную книжку «Как это решить?»[①], рассчитанную на учителей математики и учащихся. Настоящая книга, изданная в двух томах в Принстоне (США) в 1954 г., представляет собою итог многолетней работы автора, научной и педагогической, над вопросами о путях математического творчества.

Исследование такого рода естественно отличается от обычных математических работ. Оно основано на наблюдении и обобщении, на попытках проникнуть в творческую лабораторию великих математиков, придумать и поставить подходящий эксперимент. Иными словами, методы исследования здесь, собственно, те же, что и вообще в естествознании. И самое замечательное, что в своем математическом творчестве математик так же пользуется наблюдением и обобщением, гипотезой и экспериментом, как это делает естествоиспытатель. больше

10

того, автор считает даже, что индуктивные, т. е. основанные на вышеперечисленных методах[②], рассуждения легче изучать в области математики, чем в какой-либо другой области.

В соответствии с такой установкой автора первая часть книги содержит большое число примеров разных степеней трудности (начиная от самых элементарных), обучающих пользованию индукцией и аналогией в математике. Многие из них заимствованы непосредственно из творчества великих математиков, особенно из трудов Леонарда Эйлера, 250-летие со дня рождения которого отмечалось в текущем году[③]. Обращение к трудам Эйлера звучит при этом особенно убедительно, поскольку Эйлер не только с непревзойденным до сих пор успехом пользовался индуктивными методами в математике, но и откровенно сообщал читателю пути, которыми шел в своем математическом творчестве.

Вторая часть книги содержит попытку сформулировать правила индуктивного («правдоподобного») рассуждения наподобие логических правил вывода. К каждому из этих правил автор приходит, начиная с конкретных примеров, заимствованных из математики, физики, астрономии, из судебной практики и даже из медицины. Для теоретического обоснования этих правил Пойа привлекает теорию вероятностей, просто и популярно излагая в этой связи нужный ему материал из этой области. Если первая часть книги представляет особый интерес именно в связи с математикой, то вторая относится преимущественно к вопросам индуктивной логики и ее применений в любых областях науки и жизни. книга написана так, что даже в тех случаях, когда автор предполагает знакомство с математикой, читатель, не обладающий специальными математическими знаниями, тем не менее легко может уследить за основной мыслью автора. Ее могут поэтому с успехом читать люди самых разнообразных специальностей. К тому же вторую часть можно читать совершенно независимо от первой. Но читатель, который начнет со второй части и затем обратится к первой, увидит, сколь интересный материал содержится именно в первой части.

Я позволю себе сделать здесь несколько замечаний по поводу методологических установок автора. Попыткам использовать теорию веро-

11

ятностей для обоснования индуктивной логики, истолковав вероятность как степень правдоподобности (или вводя термин вероятность в различных смыслах: «вероятность-один» как степень правдоподобности и «вероятность-два», основанную на понятии частоты, см. R. Carnap, Logical Foundations of Chicago, 1950), посвящена в настоящее время большая литература. В книге Пойа мы не найдем строгого обоснования выдвигаемой им теории. Но ряд моментов в ней звучит весьма убедительно для читателя-материалиста. Автор озабочен прежде всего не субъективной, но объективной оценкой степени правдоподобности того или иного аргумента. Он подчеркивает, что хотя к правдоподобностям применимы некоторые правила, заимствованные из теории вероятностей, правдоподобности нельзя все же рассматривать как числа. Достоверно истинное высказывание имеет, правда, максимальную правдоподобность (которую можно назвать «единицей», а достоверно ложное — минимальную, «нуль»), но тем не менее могут существовать и несравнимые (по силе доводов) правдоподобности (в качестве таковых автор приводит, например, правдоподобности а) теоремы Гольдбаха о сумме двух нечетных простых чисел и б) утверждение, что викинги высадились на американском материке за несколько сот лет до Колумба). правдоподобности[④] образуют, таким образом, лишь частично упорядоченное множество, почему их и нельзя оценивать числами, множество которых линейно упорядочено[⑤]). (В соответствии с этим отличием правдоподобности от вероятности автор — к сожалению, весьма неопределенно — говорит о различии «качественной» и «количественной» теории вероятностей.) Отметим наконец, что статистические закономерности, основанные на обычном понятии вероятности (как «частоты дальнего действия»), Пойа отнюдь не противополагает — в качестве единственно

12

приемлемых — причинным закономерностям (как это часто делается в философской идеалистической литературе), а наоборот, учит употреблять статистические методы для обоснования причинных («физических») закономерностей — для исключения возможности случайного совпадения.

Но манера автора трактовать «качественную» теорию вероятностей — пусть хотя бы лишь из побуждений сделать изложение доступным для читателя, не знакомого с понятием частично упорядоченного множества, — звучит уже отнюдь не материалистически. Так, на стр. 348 автор начинает с того, что констатирует невозможность приписать P {A} — правдоподобности утверждения A в глазах м-ра Кто-нибудь — определенное числовое значение, после чего предлагает тем не менее рассматривать P {A} как определенную дробь

0 < P {A} < 1,

числового значения который мы, однако, не знаем (и знать не можем!). Именно это незнание конкретного числового значения и должно здесь отличать у автора «качественный» подход к теории вероятностей от «количественного», между тем как рассмотрение P {A} как «определенной положительной дроби» должно помочь распространить на правдоподобности нужные автору законы и правила теории вероятностей. В дальнейшем (см. особенно разделы: «7. Почему не количественно?» и «8. Бесконечно малые правдоподобности?» примечаний к главе XV) автор вносит, правда, необходимые уточнения. Однако зачем, хотя бы на время, создавать у читателя впечатление, будто допускается существование каких-то вещей в себе (определенных числовых оценок правдоподобности), принципиально непознаваемых? Ведь из дальнейшего ясно, что автор отнюдь не считает P {A} числом!

Аналогичные замечания можно было бы сделать и в применении к некоторым другим местам книги. Иногда оговаривая их в примечаниях редактора, мы, однако, не ставили перед собой задачи оговорить все места, по поводу которых редактору хотелось бы высказать какие-либо критические замечания.

В отличие от большинства математических книг, книгу Пойа можно читать как увлекательную беллетристику. Но над ней можно и серьезно работать. Указания о том, как работать над этой книгой, читатель найдет в предисловии автора и в его советах читателю.

13

На этот счет мне хотелось бы только заметить следующее. Во второй части каждой главы автор предлагает задачи и темы для самостоятельной работы читателя — от самых легких до очень трудных. При первом чтении, конечно, можно не решать полностью задач, предлагаемых автором, но чтобы правильно понять его мысль, изложенную в первой части главы, необходимо обычно уже при первом чтении возможно внимательнее просмотреть и материал, помещенный во второй ее части (а при более внимательном чтении необходимо ознакомиться и с предлагаемыми автором решениями). Вопреки некоторым рекомендациям автора, повторяю, что и читатель малознакомый с математикой может начинать чтение со второго тома книги (посвященного логике правдоподобных умозаключений и теории вероятностей), принимая на веру вещи, предполагающие более специальные математические знания.

Над вопросом, возможна ли теория, предметом которой являются не математические доказательства, а способы догадываться о таких доказательствах, открывать математические истины и решать математические задачи, люди бьются еще со времен античной древности. Вопросы этого рода не могут не интересовать каждого преподавателя математики или обучающегося ей. Будем же надеяться, что книга Пойа будет полезна и доставит удовольствие широкому кругу советских читателей.

С. А. Яновская

ПРЕДИСЛОВИЕ

Эта книга имеет различные тесно связанные между собой цели. В первую очередь она предназначена для того, чтобы помочь учащимся и преподавателям математики в одном важном вопросе, которому обычно не уделяют должного внимания. Однако в известном смысле она представляет и философский этюд. Она является также продолжением и требует продолжения. Я последовательно коснусь этих ее особенностей.

1. Строго говоря, все наши знания за пределами математики и доказательной логики (которая фактически является ветвью математики) состоят из предположений[⑥]. Конечно, существуют предположения и предположения. Есть в высшей степени достойные и надежные предположения, например, те, которые выражены в некоторых общих законах физики. Бывают другие предположения, не являющиеся ни надежными, ни достойными, и некоторые из них способны привести вас в ярость, когда вы прочитаете их в газете. И между теми и другими существуют всякого рода предположения, предчувствия и догадки.

Мы закрепляем свои математические знания доказательными рассуждениями, но подкрепляем свои предположения правдоподобными рассуждениями. Математическое доказательство является доказательным рассуждением, а индуктивные доводы физика, косвенные улики юриста, документальные доводы историка и статистические доводы экономиста относятся к правдоподобным рассуждениям.

Различие между этими двумя типами рассуждений велико и многообразно. Доказательное рассуждение надежно, неоспоримо и окончательно. Правдоподобное рассуждение рискованно, спорно и условно.

15

Доказательные рассуждения пронизывают науки как раз в той же мере, что и математика, но сами по себе (как и сама по себе математика) не способны давать существенно новые знания об окружающем нас мире. Все новое, что мы узнаем о мире, связано с правдоподобными рассуждениями, являющимися единственным типом рассуждений, которым мы интересуемся в повседневных делах. Доказательное рассуждение имеет жесткие стандарты, кодифицированные и выясненные логикой (формальной, или доказательной логикой), являющейся теорией доказательных рассуждений. Стандарты правдоподобных рассуждений текучи, и нет никакой теории таких рассуждений, которая могла бы по ясности сравниться с доказательной логикой или обладала бы сравнимой с ней согласованностью.

2. Заслуживает нашего внимания другой момент, касающийся этих двух типов рассуждений. Всякий знает, что математика предоставляет прекрасную возможность научиться доказательным рассуждениям, но я утверждаю также, что в обычных учебных планах учебных заведений нет предмета, который давал бы сравнимую возможность научиться правдоподобным рассуждениям. Я обращаюсь ко всем, кто обучается математике, элементарной или высшей, и заинтересован в овладении ею, и говорю: «Конечно, будем учиться доказывать, но будем также учиться догадываться».

Это звучит немного парадоксально, и я должен подчеркнуть несколько обстоятельств, чтобы избежать возможных недоразумений.

Математика рассматривается как доказательная наука. Однако это только одна из ее сторон. Законченная математика, изложенная в законченной форме, выглядит как чисто доказательная, состоящая только из доказательств. Но математика в процессе создания напоминает любые другие человеческие знания, находящиеся в процессе создания. Вы должны догадаться о математической теореме, прежде чем ее докажете; вы должны догадаться об идее доказательства, прежде чем проведете его в деталях. Вы должны сопоставлять наблюдения и следовать аналогиям; вы должны пробовать и снова пробовать. Результат творческой работы математика — доказательное рассуждение, доказательство; но доказательство открывается с помощью правдоподобного рассуждения, с помощью догадки. Если обучение математике в какой-то степени отражает то, как создается математика, то в нем должно найтись место для догадки, для правдоподобного умозаключения.

Как мы сказали, существует два типа рассуждений: доказательное рассуждение и правдоподобное рассуждение. Замечу, что они не противоречат друг другу; напротив, они друг друга дополняют. В строгом рассуждении главное — отличать доказательство от догадки, обоснованное доказательство от необоснованной попытки. В правдоподобном рассуждении главное — отличать одну догадку от другой, более разумную догадку от менее разумной. Если вы вдумаетесь в это отличие, то оба типа рассуждений могут стать более ясными.

16

Серьезный человек, изучающий математику, намеревающийся сделать математику делом своей жизни, должен учиться доказательным рассуждениям; это его профессия и отличительный признак его науки. Однако для настоящего успеха он должен учиться и правдоподобным рассуждениям; это тот тип рассуждений, от которого будет зависеть его творческая работа. Человек, занимающийся математикой как вспомогательным предметом или как любитель, также должен получить некоторое знакомство с доказательными рассуждениями; может быть, у него не будет особой надобности непосредственно их применять, но он должен овладеть стандартом, с которым он мог бы сравнивать всевозможные выдвигаемые в качестве доказательств доводы, встречающиеся ему в современной жизни. Но во всех его начинаниях ему будут нужны правдоподобные рассуждения. Во всяком случае, человеку, изучающему математику и желающему проявить себя в этой области, какими бы ни оказались его дальнейшие интересы, следует попытаться научиться обоим типам рассуждений, доказательному и правдоподобному.

3. Я не верю, что существует абсолютно гарантированный метод, позволяющий научить догадываться. Во всяком случае, если такой метод и существует, то мне он не известен, и уж, конечно, я не претендую на то, чтобы изложить его на последующих страницах. Действенное применение правдоподобных рассуждений есть практический навык, и ему, как и всякому другому практическому навыку, учатся путем подражания и практики. Я попытаюсь сделать все от меня зависящее, чтобы помочь читателю, очень желающему научиться правдоподобным рассуждениям, но все, что я могу предложить, это только примеры для подражания и возможность попрактиковаться.

В этой книге я часто буду обсуждать математические открытия, большие и малые. Я не могу рассказать подлинную историю того, как происходило открытие, потому что этого в действительности никто не знает. Однако я попытаюсь придумать правдоподобную историю того, как открытие могло произойти. Я попытаюсь выявить мотивы, лежащие в основе открытия, правдоподобные умозаключения, которые к нему привели, короче, все, что заслуживает подражания. Конечно, я попытаюсь убедить читателя; это моя обязанность как преподавателя и как автора. Однако я буду с читателем совершенно честен в том, что действительно существенно: я буду стараться убедить его только в том, что мне представляется истинным и полезным.

За каждой главой следуют примеры и примечания. Примечания относятся к вопросам, слишком техническим или слишком тонким для текста главы, или к вопросам, лежащим несколько в стороне от главной линии рассуждения. Некоторые из упражнений дают читателю возможность заново рассмотреть детали, только намеченные в тексте. Однако большая часть упражнений дает возможность читателю вывести свои собственные правдоподобные заключения.

17

Перед тем как взяться за какую-нибудь более трудную задачу, предложенную в конце главы, читателю следует внимательно прочитать соответствующие части главы и, кроме того, бегло просмотреть соседние задачи; то или другое может содержать ключ. Чтобы обеспечить читателя такими ключами (или скрыть их от него) с наибольшей пользой для обучения, большое внимание было уделено не только содержанию и форме предлагаемых задач, но и их расположению. Фактически на расстановку этих задач ушло значительно больше времени и заботы, чем можно было бы себе представить или посчитать нужным, глядя со стороны.

Чтобы охватить широкий круг читателей, я пытался проиллюстрировать каждый важный вопрос как можно более элементарным примером. Однако в нескольких случаях я был вынужден взять не слишком элементарный пример, чтобы подкрепить утверждение достаточно убедительно. В действительности я чувствовал, что должен привести и примеры, имеющие исторический интерес, и примеры, обладающие настоящей математической красотой, и примеры, иллюстрирующие параллелизм методов в других науках или в повседневной жизни.

Следует добавить, что многие из приведенных рассказов получили свою окончательную форму в результате своего рода неформального психологического эксперимента. Я обсуждал предмет с несколькими различными студенческими группами, часто прерывая свое изложение вопросами вроде следующего: «Хорошо, а что бы вы сделали в такой ситуации?» Некоторые места, включенные в текст книги, были подсказаны ответами моих слушателей или моя первоначальная версия изменялась каким-нибудь другим образом под влиянием реакции моей аудитории.

Короче говоря, я пытался употребить весь свой опыт исследователя и преподавателя, чтобы дать читателю подходящую возможность для разумного подражания и для самостоятельной работы.

4. Примерами правдоподобных рассуждений, собранными в этой книге, можно воспользоваться и для другой цели: они могут пролить некоторый свет на философскую проблему, являющуюся предметом оживленных споров: проблему индукции. Вот главный вопрос: существуют ли для индукции правила? Некоторые философы говорят: «Да», — большинство ученых думает: «Нет». Чтобы обсудить этот вопрос с пользой, следует иначе его поставить. Кроме того, его следует толковать иначе, с меньшей зависимостью от традиционного буквоедства или от новомодного формализма, но в более тесном контакте с практикой ученых. Заметим прежде всего, что индуктивное рассуждение есть частный случай правдоподобного рассуждения. Заметим также (современные авторы почти забыли это, но некоторые старые, такие как Эйлер и Лаплас, ясно осознавали), что роль индуктивных доводов в математическом исследовании сходна с их ролью в физическом исследовании. После этого вы сумеете обнаружить, что некоторые сведения об индуктивных рассуждениях

18

возможно получить путем наблюдения и сравнения примеров правдоподобных рассуждений в математических вопросах. И таким образом открывается дверь для индуктивного исследования индукции.

Когда биолог пытается исследовать какую-нибудь общую проблему, скажем, генетики, ему очень важно выбрать какой-нибудь специальный вид растения или животного, вполне пригодный для экспериментального изучения его проблемы. Когда химик намеревается исследовать какую-нибудь общую проблему, касающуюся, скажем, скорости химических реакций, ему очень важно выбрать какие-нибудь специальные вещества, на которых было бы удобно проделать эксперименты, уместные в его проблеме. Выбор подходящего экспериментального материала чрезвычайно важен для индуктивного исследования любой проблемы. Мне кажется, что математика в некоторых отношениях является наиболее подходящим экспериментальным материалом для изучения индуктивных рассуждений. Это изучение вызывает необходимость некоторого рода психологических экспериментов: вы должны испытать на опыте, какое влияние на вашу веру в рассматриваемое предположение оказывают различные виды доводов. Благодаря своей неотъемлемой простоте и ясности, математические объекты подходят для этого рода психологического эксперимента гораздо лучше, чем объекты из любой другой области. На следующих страницах читатель будет иметь полную возможность в этом убедиться.

С точки зрения философии, я думаю, лучше рассматривать более общую идею правдоподобного рассуждения вместо частного случая индуктивного рассуждения. Мне кажется, что собранные в этой книге примеры постепенно подготавливают определенный и вполне удовлетворительный аспект правдоподобного рассуждения. Однако я не хочу навязывать свои взгляды читателю. Фактически я даже не формулирую их в первом томе; я хочу, чтобы примеры говорили сами за себя. Первые четыре главы второго тома посвящены более явному общему рассмотрению правдоподобных рассуждений. Здесь я формально устанавливаю схемы правдоподобных умозаключений, возникающие из приведенных примеров, пытаюсь систематизировать эти схемы и обозреть некоторые из их взаимных связей и их связей с идеей вероятности.

Я не знаю, заслуживает ли содержание этих четырех глав право называться философией. Если это философия, то это, несомненно, немудреный вид философии, больше имеющий дело с пониманием конкретных примеров и конкретного поведения людей, чем с толкованием общностей. Я еще меньше, конечно, знаю, какой окажется окончательная оценка моих взглядов. Однако я чувствую довольно сильную уверенность в том, что мои примеры могут быть полезны для любого разумного, непредубежденного человека, изучающего индукцию или правдоподобные рассуждения, который желает сформировать свои взгляды в тесном контакте с наблюдаемыми фактами.

19

5. Эта работа о Математике и Правдоподобных рассуждениях, которую я всегда рассматривал как целое, естественно распадается на две части: Индукция и Аналогия в Математике (том I) и Схемы Правдоподобных Умозаключений (том II). Для удобства изучающих они выпускаются отдельными томами[⑦] Том I полностью независим от тома II, и я думаю, что многие учащиеся захотят его тщательно продумать перед тем, как читать том II. (В русском издании оба тома объединены в одной книге.) В нем — бо́льшая часть математического «мяса» этого сочинения, и он поставляет «данные» для индуктивного исследования индукции в томе II. Некоторые читатели, более умудренные и опытные в математике, захотят, быть может, непосредственно перейти к тому II, и для них будет удобно иметь его отдельно. Для облегчения ссылок нумерация глав в обоих томах сплошная. Я не снабдил книгу указателем, так как указатель заставил бы сделать терминологию более жесткой, чем это желательно в такого рода сочинении. Я уверен, что оглавление дает удовлетворительный путеводитель по книге.

Эта работа является продолжением моей более ранней книги How to Solve It[⑧][3]. Читателю, интересующемуся предметом, следует прочитать обе книги, но порядок не имеет большого значения. Настоящий текст составлен так, что его можно читать независимо от предыдущей работы. Фактически в этой книге имеется лишь несколько прямых ссылок на прежнюю и при первом чтении на них можно не обращать внимания. Однако косвенные ссылки на предыдущую книгу имеются почти на каждой странице и почти в каждом предложении некоторых страниц. В сущности эта работа дает многочисленные упражнения и некоторые более серьезные иллюстрации к предыдущей, в которой ввиду ее размера и элементарного характера не было для них места.

Настоящая книга связана также со сборником задач по анализу, принадлежащим Г. Сеге и автору (см. библиографию). Задачи в этом сборнике тщательно сгруппированы в таком порядке, что они взаимно подкрепляют друг друга, дают ключи друг другу, в совокупности охватывают определенную тему и предоставляют читателю возможность попрактиковаться в различных ходах, важных в решении задач. В подходе к задачам настоящая книга следует методу изложения, начало которому было положено в упомянутом сборнике, и эта связь имеет не столь уж малое значение.

Две главы во втором томе настоящей книги имеют дело с теорией вероятностей. Первая из этих глав отчасти связана с элементарным изложением исчисления вероятностей, написанным автором несколько лет тому назад (см. библиографию). Лежащие в основании взгляды на вероятность и отправные пункты — те же самые, в остальном соприкосновения мало.

20

Некоторые из взглядов, изложенных в этой книге, были выражены ранее в моих статьях, указанных в библиографии. В текст книги были включены обширные выдержки из статей №№ 4, 6, 8, 9 и 10. Я приношу признательность и мою глубокую благодарность издателям American Mathematical Monthly, Etudes de Philosophie des Sciences en Hommage à Ferdinand Gonseth и Proceedings of the International Congress of Mathematicians 1950, которые любезно дали разрешение воспроизвести эти выдержки.

Многие части этой книги были изложены в моих лекциях, некоторые — несколько раз. В некоторых местах и в некоторых отношениях я сохранил тон устного изложения. Я не думаю, что такой тон вообще желателен при печатном изложении математики, но в настоящем случае это может быть подходящим или по крайней мере простительным.

6. Последняя глава второго тома настоящей книги, имеющая дело с Изобретением и Обучением, в более явной форме связывает содержание с прежней работой автора и указывает на возможное продолжение.

Действенное применение правдоподобных рассуждений играет существенную роль в решении задач. Настоящая книга пытается проиллюстрировать эту роль на многих примерах, но остаются другие стороны решения задач, нуждающиеся в подобной иллюстрации.

Многие вопросы, затронутые здесь, нуждаются в дальнейшей разработке. Мои взгляды на правдоподобные рассуждения следовало бы сопоставить со взглядами других авторов, исторические примеры следовало бы рассмотреть более тщательно, взгляды на изобретение и обучение следовало бы изучить, насколько это возможно, методами экспериментальной психологии[⑨], и так далее. Остаются другие такого рода задачи, но некоторые из них могут оказаться неблагодарными.

Эта книга не учебник. Однако я надеюсь, что со временем она окажет влияние на обычное изложение в учебниках и выбор их круга вопросов. Задача заново написать обычные учебники, придерживаясь намеченного направления, не должна быть неблагодарной.

7. Я хочу выразить свою признательность издательству Принстонского университета за тщательное печатание и особенно г-ну Герберту С. Бэйли младшему, директору издательства, за сочувственную помощь в некоторых вопросах. Я весьма обязан также г-же Присилле Фейген за перепечатку рукописи на машинке и д-ру Юлиусу Г. Барону за его любезную помощь при чтении корректур.

Стэнфордский университет, май 1953 г.

Дьердь Пойа

СОВЕТЫ ЧИТАТЕЛЮ

Параграф 2 гл. VII в той же главе VII цитируется как § 2, но как § 7.2 в любой другой главе. Пункт (3) § 5 гл. XIV в той же главе XIV цитируется как § 5 (3), но как § 14.5 (3) в других главах. На пример 26 гл. XIV мы ссылаемся в той же главе, как на пример 26, но как на пример 14.26 в остальных главах.

Для чтения существенных частей текста может быть достаточно некоторого знания элементарной алгебры и геометрии. Почти для всего текста и большей части примеров и примечаний достаточно хорошего знания элементарной алгебры и геометрии и некоторого знания аналитической геометрии и математического анализа, включая пределы и бесконечные ряды. Однако в нескольких эпизодических замечаниях в тексте, в некоторых предлагаемых задачах и в отдельных примечаниях предполагаются более глубокие знания. Обычно в этих случаях делается какое-нибудь предупреждение.

Более подготовленный читатель, пропустивший те отделы, которые кажутся ему слишком элементарными, может потерять больше, чем менее подготовленный читатель, который пропустит отделы, показавшиеся ему слишком сложными.

Некоторые (не очень трудные) детали доказательств часто без предупреждения опускаются. Должным образом подготовленный к этой возможности читатель, обладающий хорошими критическими навыками, не должен от этого пострадать.

Некоторые из задач, предложенных для решения, очень легки, но некоторые довольно трудны. Наводящие соображения, которые могут облегчить решение, заключены в квадратные скобки [ ]. Правильный путь решения могут подсказывать соседние задачи. Особое внимание следует обратить на вводные замечания, предшествующие примерам в некоторых главах или же первой или второй части таких примеров.

Решения иногда очень кратки: они предполагают, что перед тем как просмотреть напечатанное решение, читатель предпринял серьезные попытки справиться с задачей собственными силами.

Читатель, затративший на задачу большие усилия, даже если ему и не удалось ее решить, может извлечь из этого пользу. Например, он может заглянуть в решение, попытаться выделить то, что ему кажется ключевой идеей, отложить книгу и затем попытаться разработать решение.

22

В некоторых местах эта книга изобилует чертежами или дает небольшие промежуточные шаги вывода. Цель этого — сделать наглядной эволюцию фигуры или формулы: см., например, рис. 16.1—16.5. Однако нет такой книги, которая содержала бы достаточно фигур или формул. Читатель может захотеть прочитать какое-нибудь место «в первом приближении» или более тщательно. Во втором случае, у него под рукой должны быть бумага и карандаш: он должен быть готов написать или начертить любую формулу или фигуру, приведенную или только упомянутую в тексте. Поступая таким образом, он получит лучшую возможность увидеть эволюцию фигуры или формулы, понять, как различные детали способствуют окончательному результату, и запомнить весь процесс в целом.

ИНДУКЦИЯ И АНАЛОГИЯ В МАТЕМАТИКЕ

Том I

I. ИНДУКЦИЯ

Покажется немало парадоксальным приписывать большое значение наблюдениям даже в той части математических наук, которая обычно называется чистой математикой, так как существует распространенное мнение, что наблюдения ограничиваются физическими объектами, которые воздействуют на наши чувства. Поскольку мы должны относить числа к одному лишь чистому разуму, мы едва ли можем понять, как наблюдения и квазиэксперименты могут быть полезны в исследовании природы чисел. Однако в действительности, как я здесь покажу, приведя очень веские доводы, свойства чисел, известные сегодня, по большей части были открыты путем наблюдения и открыты задолго до того, как их истинность была подтверждена строгими доказательствами. Имеется даже много свойств чисел, с которыми мы хорошо знакомы, но которые мы все еще не в состоянии доказать; только наблюдения привели нас к их познанию. Отсюда мы видим, что в теории чисел, которая все еще очень несовершенна, наши самые большие надежды мы можем возлагать на наблюдения; они непрерывно будут вести нас к новым свойствам, которые позже мы будем стараться доказать. Этот вид знания, которое подкрепляется только наблюдениями и все еще не доказано, следует тщательно отличать от истины; оно, как мы обычно говорим, приобретается индукцией. Однако мы видели случаи, когда простая индукция вела к ошибке. Поэтому мы должны проявлять большую осторожность, чтобы не принять за истинные такие свойства чисел, которые мы открыли путем наблюдения и которые подкрепляются одной лишь индукцией. В действительности мы должны пользоваться таким открытием, как возможностью более точно исследовать эти открытые свойства и доказать их или опровергнуть: в обоих случаях мы можем научиться кое-чему полезному. — Эйлер[⑩]

1. Опыт и представление. Опыт вносит изменения в человеческие представления. Мы учимся, исходя из опыта, или, вернее, должны учиться, исходя из опыта. Наилучшим возможным образом воспользоваться опытом — одна из великих задач человека, а трудиться для ее решения — подлинное призвание ученых.

Ученый, заслуживающий этого имени, старается извлечь из данного опыта наиболее правильное представление и накопить наиболее подходящий опыт для того, чтобы установить правильное представление о данном вопросе. Метод, с помощью которого ученый имеет дело с опытом, обычно называется индукцией. Особенно ясные примеры метода индукции можно найти в математическом исследовании. В следующем параграфе мы приступаем к рассмотрению одного простого примера.

26

2. Наводящие контакты. Индукция часто начинается с наблюдения. Натуралист может наблюдать жизнь птиц, кристаллограф — формы кристаллов. Математик, интересующийся теорией чисел, наблюдает свойства чисел 1, 2, 3, 4, 5, ...

Если вы хотите наблюдать жизнь птиц так, чтобы была некоторая возможность получить интересные результаты, то вы должны быть в какой-то степени знакомы с птицами, интересоваться птицами, вы должны даже, пожалуй, любить птиц. Точно так же, если вы хотите наблюдать числа, вы должны интересоваться ими и в какой-то степени быть знакомы с ними. Вы должны различать четные и нечетные числа, должны знать квадраты 1, 4, 9, 16, 25, ... и простые числа 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ... (лучше выделить 1 как «единицу» и не причислять ее к простым числам). Даже со столь скромными знаниями вы смогли бы подметить кое-что интересное.

Случайно вы наталкиваетесь на соотношения

3 + 7 = 10,

3 + 17 = 20,

13 + 17 = 30

и замечаете между ними некоторое сходство. Вам приходит в голову, что числа 3, 7, 13 и 17 являются нечетными простыми числами. Сумма двух нечетных простых чисел есть обязательно четное число; действительно, числа 10, 20 и 30 — четные. А что можно сказать о других четных числах? Ведут ли они себя подобным же образом? Первое четное число, являющееся суммой двух нечетных простых чисел, есть, конечно,

6 = 3 + 3.

Двигаясь дальше, находим, что

8 = 3 + 5,

10 = 3 + 7 = 5 + 5,

12 = 5 +7,

14 = 3 + 11 = 7 + 7,

16 = 3 + 13 = 5 + 11.

Всегда ли так будет продолжаться? Как бы то ни было, частные случаи, которые мы наблюдали, наводят на мысль об общем утверждении: любое четное число, большее чем 4, представимо в виде суммы двух нечетных простых чисел. Поразмыслив об исключительных случаях — числах 2 и 4, которые не могут быть расщеплены в сумму двух нечетных простых чисел, мы можем предпочесть следующее менее непосредственное утверждение: любое четное

27

число, не являющееся ни простым числом, ни квадратом простого числа, представимо в виде суммы двух нечетных простых чисел.

Итак, нам удалось сформулировать предположение. Мы нашли это предположение с помощью индукции. Иными словами, оно возникло у нас в результате наблюдения, было указано отдельными частными примерами.

Эти указания являются довольно легковесными; у нас есть лишь очень слабые основания верить в свое предположение. Мы можем, однако, найти некоторое утешение в том факте, что Гольдбах, математик, впервые высказавший это предположение немногим более двухсот лет тому назад, не обладал для этого сколько-нибудь более серьезными основаниями.

Справедливо ли предположение Гольдбаха? Никто сегодня не может ответить на этот вопрос. Несмотря на огромные усилия, затраченные на выяснение этого вопроса некоторыми великими математиками, предположение Гольдбаха сегодня, как это было и в дни Эйлера, является одним из тех «многих свойств чисел, с которыми мы хорошо знакомы, но которые мы все еще не в состоянии доказать» или опровергнуть.

Взглянем теперь назад и попытаемся уловить в предыдущем рассуждении такие шаги, которые могли бы быть типичными для процесса индукции.

Сначала мы подметили некоторое сходство. Мы осознали, что 3, 7, 13 и 17 — простые, а 10, 20 и 30 — четные числа и что три соотношения 3 + 7 = 10, 3 + 17 = 20, 13 + 17 = 30 аналогичны между собой.

Следующим шагом было обобщение. От четырех чисел 3, 7, 13 и 17 мы перешли ко всем нечетным простым числам; от 10, 20 и 30 — ко всем четным числам, а затем — к возможному общему соотношению

четное число = простому числу + простое число.

Мы пришли, таким образом, к отчетливо сформулированному общему утверждению, которое, однако, является только предположением, только пробным утверждением. Это значит, что утверждение ни в какой степени не является доказанным, никак не может претендовать на истинность, оно является только попыткой подойти к истине.

Это предположение имеет, однако, некоторые наводящие точки соприкосновения, контакта с опытом, с «фактами», с «действительностью». Оно верно для некоторых конкретных чисел 10, 20, 30, а также для 6, 8, 12, 14, 16.

Этими замечаниями мы в общих чертах обрисовали первую стадию процесса индукции.

28

3. Подкрепляющие контакты. Не стоит слишком уж верить в любое недоказанное предположение, даже если оно было предложено большими авторитетами, даже если оно возникло у вас самих. Нужно попытаться доказать его или опровергнуть; нужно его испытать.

Мы испытаем предположение Гольдбаха, если исследуем какое-нибудь новое четное число и выясним, является ли оно суммой двух нечетных простых чисел или нет. Исследуем, например, число 60. Выполним «квазиэксперимент», как выражается Эйлер. Число 60 четное, но является ли оно суммой двух простых чисел? Верно ли, что

60 = 3 + простое число?

Нет, число 57 не простое. Имеет ли место

60 = 5 + простое число?

Ответ снова будет «Нет»: число 55 не простое. Если так будет продолжаться и дальше, то предположение будет подорвано. Но следующее испытание дает

60 = 7 + 53,

и 53 — простое число. Предположение подтвердилось еще в одном случае.

Противоположный результат решил бы судьбу предположения Гольдбаха раз и навсегда. Если, испытывая все простые числа до данного четного числа, например 60, вы ни в одном случае не приходите к разложению его в сумму двух простых чисел, то тем самым вы безвозвратно подрываете предположение. Подтвердив предположение в случае числа 60, вы не можете прийти к столь же определенному заключению. Вы, безусловно, не докажете теорему с помощью единственного подтверждения. Естественно, однако, истолковать такое подтверждение, как благоприятный признак, говорящий в пользу предположения, делающий его более правдоподобным, хотя, конечно, остается вашим личным делом, какой вес вы придадите этому благоприятному признаку.

Возвратимся на минуту к числу 60. После того как были испытаны простые числа 3, 5 и 7, мы можем испытать остающиеся простые числа до 30. (Очевидно, нет необходимости идти дальше 30 = 60/2, так как одно из двух простых чисел, сумма которых равна 60, должно быть меньше 30.) Мы получим, таким образом, все разложения 60 в сумму двух простых чисел:

60 = 7 + 53 = 13 + 47 = 17 + 43 = 19 + 41 = 23 + 37 = 29 + 31.

Мы можем действовать систематически и исследовать четные числа одно за другим, как только что исследовали число 60. Результат

29

мы можем записать в виде следующей таблицы:

6 =	3 +	3
8 =	3 +	5
10 =	3 +	7	=	5 +	5
12 =	5 +	7
14 =	3 +	11	=	7 +	7
16 =	3 +	13	=	5 +	11
18 =	5 +	13	=	7 +	11
20 =	3 +	17	=	7 +	13
22 =	3 +	19	=	5 +	17 = 11 + 11
24 =	5 +	19	=	7 +	17 = 11 + 13
26 =	3 +	23	=	7 +	19 = 13 + 13
28 =	5 +	23	=	11 +	17
30 =	7 +	23	=	11 +	19 = 13 + 17.

Предположение подтверждается во всех случаях, которые мы здесь рассмотрели. Каждое подтверждение, удлиняющее таблицу, усиливает предположение, делает его в большей мере внушающим доверие, увеличивает его правдоподобие. Конечно, никакое число таких подтверждений не могло бы его доказать.

Нам нужно исследовать собранные наблюдения, сравнить их и сопоставить, нужно поискать какой-то ключ, быть может скрытый за ними. В нашем случае очень трудно обнаружить в таблице какой-либо ключ, который мог бы оказать нам существенную помощь. Тем не менее, рассматривая таблицу, мы можем яснее осознать смысл предположения. Таблица показывает, сколькими способами входящие в нее четные числа могут быть представлены как сумма двух простых чисел (6 — одним, 30 — тремя). Число таких представлений четного числа 2n кажется «неправильно возрастающим» вместе с n. Предположение Гольдбаха выражает надежду, что как бы далеко мы ни расширяли таблицу, число представлений никогда не упадет до 0.

Среди исследованных нами частных случаев мы можем различать две группы: те, которые предшествовали формулировке предположения, и те, которые были рассмотрены после нее. Первые навели на предположение, вторые подкрепили его. И те, и другие создают некоторого рода контакт между предположением и «фактами». Таблица не делает различия между «наводящими» и «подкрепляющими» точками соприкосновения.

Посмотрим теперь снова на предыдущее рассуждение и попытаемся заметить в нем черты, типичные для процесса индукции.

Высказав предположение, мы пытались выяснить, является ли оно верным или ошибочным. Наше предположение было утверждением общего характера, возникшим из некоторых частных примеров,

30

в которых оно оказалось верным. Мы исследовали еще несколько частных случаев. Поскольку обнаружилось, что предположение справедливо для всех рассмотренных примеров, наша вера в него возросла.

Мы делали, как мне кажется, только то, что обычно делают разумные люди. Поступая таким образом, мы, по-видимому, принимаем принцип: предположительное общее утверждение становится более правдоподобными, если оно подтверждается для нового частного случая.

Не этот ли принцип лежит в основе процесса индукции?

4. Индуктивный подход. В нашей личной жизни мы часто цепляемся за иллюзии. Иными словами, мы не смеем исследовать некоторые представления, которые легко могли бы быть опровергнуты опытом, потому что боимся нарушить свое душевное равновесие. Возможны обстоятельства, в которых не является неразумным цепляться за иллюзии[4], но в науке мы нуждаемся в совершенно ином подходе, в индуктивном подходе. Этот подход имеет целью приспособление наших представлений к нашему опыту в такой степени, в какой это возможно. Он требует беспрекословного предпочтения для того, что фактически существует. Он требует готовности к подъему от наблюдений к обобщениям и готовности к спуску от наиболее широких обобщений к наиболее конкретным наблюдениям. Он требует говорить «быть может» и «возможно» с тысячей различных оттенков. Он требует многих других вещей, и особенно следующих трех.

Во-первых, мы должны быть готовы пересмотреть любое из наших представлений.

Во-вторых, мы должны изменить представление, когда имеются веские обстоятельства, вынуждающие его изменить.

В-третьих, мы не должны изменять представления произвольно, без достаточных оснований.

Эти принципы звучат довольно тривиально. Но нужны довольно необычные достоинства, чтобы их придерживаться.

Первый принцип требует «мужества ума». Вам нужно мужество, чтобы пересмотреть ваши представления. Галилей, бросивший вызов предрассудку своих современников и авторитету Аристотеля, являет собой великий пример мужества ума.

Второй принцип требует «честности ума». Оставаться верным своему предположению, ясно опровергнутому опытом, только потому, что это мое собственное предположение, было бы нечестно.

Третий принцип требует «мудрой сдержанности». Изменить представление без серьезного исследования, например, только ради моды, было бы глупо. Но мы не имеем ни времени, ни сил серьезно исследовать все наши представления. Поэтому будет мудро посвятить нашу повседневную работу, наши вопросы и наши живые сомнения тем представлениям, которые мы можем разумно надеяться исправить.

31

«Не верь ничему, но сомневайся только в том, в чем стоит сомневаться».

Смелость ума, честность ума и мудрая сдержанность — моральные достоинства ученого.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ I

1[5]. Догадайтесь, в соответствии с каким правилом выбираются члены последовательности

11, 31, 41, 61, 71, 101, 131, ... .

2. Рассмотрите таблицу:

1	=	0	+	1
2 + 3 + 4	=	1	+	8
5 + 6 + 7 + 8 + 9	=	8	+	27
10 + 11 + 12 + 13 + 14 + 15 + 16	=	27	+	64

Догадайтесь, к какому общему закону подводят эти примеры; выразите его в подходящих математических обозначениях и докажите.

3. Рассмотрите значения последовательных сумм

1, 1 + 3, 1 + 3 + 5, 1 + 3 + 5 + 7, ...

Имеется ли простое правило?

4. Рассмотрите значения последовательных сумм

1, 1 + 8, 1 + 8 + 27, 1 + 8 + 27 + 64, ...

Имеется ли простое правило?

5. Три стороны треугольника имеют соответственно длины l, m и n. Числа l, m и n — целые положительные, l ≤ m ≤ n. Найдите число различных треугольников указанного вида для данного n. (Возьмите n = 1, 2, 3, 4, 5, ...) Найдите общий закон, управляющий зависимостью числа треугольников от n.

6. Три первых члена последовательности 5, 15, 25, ... (чисел, оканчивающихся на 5) делятся на 5, Делятся ли на 5 и следующие члены?

Три первых члена последовательности 3, 13, 23, ... (чисел, оканчивающихся на 3) являются простыми числами. Будут ли простыми числами и следующие члены?

7. С помощью формальных вычислений находим

(1 + 11x + 21 x² + 31x³ + 41x⁴ + 51 x⁵ + 61x⁶ + ...)^–1 = 1 – x – x² – 3x³ – 13x⁴ – 71x⁵ – 461x⁶ ...

Естественно возникают два предположения относительно следующих коэффициентов степенного ряда, стоящего в правой части: (1) все они отрицательны; (2) все они простые числа. Одинаково ли эти два предположения заслуживают доверия?

8. Положим

Мы найдем, что для

n	= 0	1	2	3	4	5	6	7	8	9
An	= 1	1	1	2	4	14	38	216	600	6240.

Сформулируйте предположение.

9. Великий французский математик Ферма рассмотрел последовательность

5, 17, 257, 65 537, …

32

с общим членом 2^2ⁿ+1. Он заметил, что первые четыре члена, соответствующие n = 1, 2, 3 и 4, являются простыми числами. Он предположил, что следующие члены также являются простыми числами. Хотя он и не доказал этого, он чувствовал такую уверенность в справедливости своего предположения, что бросил вызов Валлису и другим английским математикам, предлагая его доказать. Однако Эйлер нашел, что уже следующий член, 2³² + 1, соответствующий n = 5, не является простым числом[⑪]: он делится на 641. См. цитату из Эйлера в начале этой главы: «Однако мы видели случаи, когда простая индукция вела к ошибке».

10. Проверяя предположение Гольдбаха для 2n = 60, мы последовательно испытывали простые числа p до n = 30. Однако мы могли бы также испытывать простые числа p между n = 30 и 2n = 60. Какой прием скорее всего окажется более выгодным для бо́льших n?

11. В словаре вы найдете среди объяснений слов «индукция», «эксперимент» и «наблюдение» предложения вроде следующих:

«Индукция есть выведение общего закона из частных случаев, или предъявление фактов, чтобы доказать общее утверждение».

«Эксперимент есть прием для проверки гипотез».

«Наблюдение есть точное прослеживание и регистрирование явлений в том виде, как они появляются в природе, по отношению к причине и результату или взаимным связям».

Применимы ли эти описания к нашему примеру, рассмотренному в §§ 2 и 3?

12. Да и нет. Математик, подобно натуралисту, проверяя некоторые следствия предполагаемого общего закона с помощью нового наблюдения, обращается с вопросом к Природе: «Я подозреваю, что этот закон верен. Верен ли он?» Если следствие ясно опровергается, то закон не может быть верен. Если следствие ясно подтверждается, то имеется некоторое указание, что закон может быть верен. Природа может ответить «Да» или «Нет», но она шепчет один ответ и громогласно произносит другой; ее «Да» условно, ее «Нет» определенно.

13. Опыт и поведение. Опыт вносит изменения в поведение человека. Вместе с тем опыт вносит изменения в человеческие представления. Поведение человека и его представления не независимы. Поведение часто является результатом представлений, представления — это потенциальное поведение. Однако вы можете видеть поведение другого человека, но не можете видеть его представлений. Поведение легче наблюдать, чем представления. Каждый знает поговорку: «Кто обжегся на молоке, тот дует на воду»[⑫], выражающую как раз то, что мы сказали: опыт вносит изменения в поведение человека.

Впрочем, он вносит изменения и в поведение животных.

Неподалеку от моего дома есть гадкая собака, которая лает и бросается на людей безо всякого повода. Но я обнаружил, что довольно легко могу себя защитить. Если я нагибаюсь и делаю вид, что поднимаю камень, то собака с визгом убегает. Так себя ведут не все собаки, и легко догадаться, какого рода опыт явился причиной такого поведения этой собаки.

Медведь в зоопарке «служит», т. е., когда вблизи находится наблюдатель, он становится в смешную позу, которая довольно часто побуждает наблюдателя бросить в клетку кусок сахара. Медведь, живущий на воле, вероятно, никогда не принимает такой нелепой позы, и легко представить, какого рода опыт привел к тому, что медведь из зоопарка научился «служить».

Полное исследование индукции должно было бы, возможно, включать и изучение поведения животных.

33

14. Логик, математик, физик и инженер. «Взгляни на этого математика, — сказал логик. — Он замечает, что первые девяносто девять чисел меньше сотни, и отсюда с помощью того, что он называет индукцией, заключает, что все числа меньше сотни.

«Физик верит, — сказал математик, — что 60 делится на все числа. Он замечает, что 60 делится на 1, 2, 3, 4, 5 и 6. Он проверяет несколько других чисел, например 10, 20 и 30, взятых, как он говорит, наугад. Так как 60 делится и на них, то он считает экспериментальные данные достаточными».

«Да, но взгляни на инженера, — возразил физик. — Инженер подозревает, что все нечетные числа простые. Во всяком случае, 1 можно рассматривать как простое число, доказывает он. Затем идут 3, 5 и 7, все, несомненно, простые. Затем идет 9 — досадный случай; 9, по-видимому, не является простым числом. Но 11 и 13, конечно, простые. Возвратимся к 9, — говорит он, — я заключаю, что 9 должно быть ошибкой эксперимента.

Совершенно очевидно, что индукция может привести к ошибке. Однако замечательно, что индукция иногда приводит к истине, хотя, по-видимому, возможность появления ошибки так подавляюще велика. Должны ли мы начать с изучения очевидных случаев, когда индукция не удается, или с изучения тех замечательных случаев, когда индукция приводит к успеху? Изучение драгоценных камней, понятно, более привлекательно, чем изучение обычных голышей, и, более того, именно драгоценные камни в гораздо большей степени, чем голыши, привели минералогов к чудесной науке кристаллографии.

II. ОБОБЩЕНИЕ, СПЕЦИАЛИЗАЦИЯ, АНАЛОГИЯ

И я больше всего дорожу Аналогиями, моими самыми верными учителями. Они знают все секреты Природы, и ими меньше всего следует пренебрегать в Геометрии. — Кеплер

1. Обобщение, специализация, аналогия и индукция. Взглянем снова на предмет индуктивного рассуждения, который мы разобрали довольно подробно (§§ 1.2, 1.3). Мы начали с того, что подметили аналогию трех соотношений:

3 + 7 = 10, 3 + 17 = 20, 13 + 17 = 30,

мы обобщили, поднявшись от 3, 7, 13 и 17 ко всем простым, а от 10, 20 и 30 ко всем четным числам, затем мы снова специализировали, спустившись к испытанию отдельных четных чисел, как например 6 или 8, или 60.

Этот первый пример крайне прост. Он совершенно правильно иллюстрирует роль обобщения, специализации и аналогии в индуктивном рассуждении. Однако мы собираемся привести менее скудные, более яркие иллюстрации, и до этого нам нужно рассмотреть обобщение, специализацию и аналогию, эти великие источники открытия, ради них самих.

2. Обобщение есть переход от рассмотрения данного множества предметов к рассмотрению большего множества, содержащего данное. Например, мы делаем обобщение, когда переходим от рассмотрения треугольников к рассмотрению многоугольников с произвольным числом сторон. Мы делаем обобщение и когда переходим от изучения тригонометрических функций острого угла к изучению тригонометрических функций произвольного угла.

Можно заметить, что в этих двух примерах обобщение осуществлялось в двух характерно различных направлениях. В первом примере, в переходе от треугольников к многоугольникам с n сторонами, мы заменяем постоянную переменной, фиксированное число 3 произвольным числом n (ограниченным только неравенством n ≥ 3). Во втором примере, в переходе от острых углов к произвольным углам α, мы отбрасываем ограничение, именно ограничение 0° < α < 90°.

Мы часто делаем обобщение, переходя от одного лишь предмета к целому классу, содержащему этот предмет.

35

3. Специализация есть переход от рассмотрения данного множества предметов к рассмотрению меньшего множества, содержащегося в данном. Например, мы специализируем, когда переходим от рассмотрения многоугольников к рассмотрению правильных многоугольников, и специализируем еще дальше, когда переходим от правильных многоугольников с n сторонами к правильному, т. е. равностороннему треугольнику.

Эти два последовательных перехода осуществлялись в двух характерно различных направлениях. В первом переходе, от многоугольников к правильным многоугольникам, мы ввели ограничение, именно потребовали, чтобы все стороны и все углы многоугольника были равны. Во втором переходе мы заменили переменный предмет конкретным, поставили 3 вместо переменного целого числа n.

Очень часто мы производим специализацию, переходя от целого класса предметов к одному предмету, содержащемуся в этом классе. Например, когда мы хотим проверить некоторое общее утверждение относительно простых чисел, мы выбираем какое-нибудь простое число, скажем, 17, и исследуем, справедливо ли это общее отверждение или нет именно для этого числа 17.

4. Аналогия. В понятиях обобщения и специализации нет ничего неясного или сомнительного. Однако, приступая к рассмотрению аналогии, мы становимся на менее прочное основание.

Аналогия есть некоторого рода сходство. Она, можно сказать, есть сходство, но на более определенном и выражаемом с помощью понятий уровне. Однако мы можем выразиться несколько более точно. Существенное различие между аналогией и другими видами сходства заключается, как мне кажется, в намерениях думающего. Сходные предметы согласуются между собой в каком-то отношении. Если вы намереваетесь свести это отношение, в котором они согласуются, к определенным понятиям, то вы рассматриваете эти сходные предметы как аналогичные. Если вам удается добраться до ясных понятий, то вы выяснили аналогию.

Сравнивая молодую женщину с цветком, поэты ощущают, я надеюсь, некоторое сходство, но обычно они не имеют в виду аналогии. Действительно, они едва ли намереваются покинуть мир эмоций и свести это сравнение к чему-то измеримому или определимому с помощью понятий.

Рассматривая в музее естественной истории скелеты различных млекопитающих, вы можете обнаружить, что все они страшны. Если в этом все сходство, которое вы между ними обнаружили, то вы видите не такую уж сильную аналогию. Однако вы можете подметить удивительно много говорящую аналогию, если рассмотрите руку человека, лапу кошки, переднюю ногу лошади, плавник кита и крыло летучей мыши — эти столь различно используемые органы — как состоящие из сходных частей, имеющих сходное отношение друг к другу.

36

Последний пример иллюстрирует наиболее типичный случай выясненной аналогии; две системы аналогичны, если они согласуются в ясно определенных отношениях соответствующих частей.

Например, треугольник на плоскости аналогичен тетраэдру в пространстве. На плоскости 2 прямые линии не могут образовать ограниченную фигуру, а 3 могут образовать треугольник. В пространстве 3 плоскости не могут образовать ограниченное тело, а 4 могут образовать тетраэдр. Отношение треугольника к плоскости такое же, как отношение тетраэдра к пространству, поскольку и треугольник, и тетраэдр ограничены минимальным числом простых ограничивающих элементов. Отсюда аналогия.

Одно из значений греческого слова «аналогиа», от которого происходит слово «аналогия», есть «пропорция». Действительно, система двух чисел 6 и 9 «аналогична» системе двух чисел 10 и 15, поскольку отношения соответствующих членов этих двух систем согласуются:

6 : 9 = 10 : 15.

Пропорциональность, или согласованность отношений соответствующих частей, которую мы интуитивно видим в геометрически подобных фигурах, является наводящим на размышления случаем аналогии.

Вот другой пример. Мы можем рассматривать треугольник и пирамиду, как аналогичные фигуры. С одной стороны, возьмите прямоугольный отрезок, с другой — многоугольник. Соедините все точки отрезка с точкой, не лежащей на содержащей отрезок прямой, и вы получите треугольник. Соедините все точки многоугольника с точкой, не лежащей в плоскости многоугольника, и вы получите пирамиду. Таким же образом мы можем рассматривать как аналогичные фигуры параллелограмм и призму. Действительно, перемещайте отрезок или многоугольник параллельно самому себе в направлении прямой, пересекающей содержащую его прямую или плоскость, и первый опишет параллелограмм, а второй — призму. У нас может возникнуть искушение выразить это соотношение соответствия между плоскими фигурами и пространственными телами с помощью некоторого рода пропорции, и если на этот раз мы не устоим от искушения, то придем к рис. 2.1. Этот рисунок видоизменяет обычный смысл некоторых символов (: и =) в том же направлении, в котором смысл слова «аналогиа» на протяжении истории языка был видоизменен от «пропорции» к «аналогии».

Последний пример поучителен еще и в другом отношении. Аналогия, особенно неполностью выясненная аналогия, может иметь не один смысл. Так, сравнивая плоскую и пространственную геометрию, мы сначала нашли, что треугольник в плоскости аналогичен тетраэдру в пространстве, а затем, что треугольник аналогичен пирамиде. Обе аналогии разумны, каждая имеет значение в своем месте. Между плоской и пространственной геометрией имеется несколько аналогий, а не всего лишь одна привилегированная аналогия.

37

Рис. 2.2 показывает, как начиная от треугольника мы можем подняться к многоугольнику с помощью обобщения, спуститься к равностороннему треугольнику с помощью специализации или перейти к различным пространственным телам с помощью аналогии — имеются аналогии во все стороны.

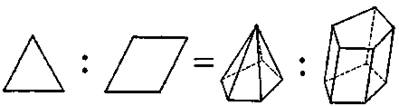
Рис. 2. 1. Соотношения аналогии на плоскости и в пространстве.

И запомните: не пренебрегайте смутными аналогиями. Однако если вы хотите, чтобы они заслуживали уважение, попытайтесь их выяснить.

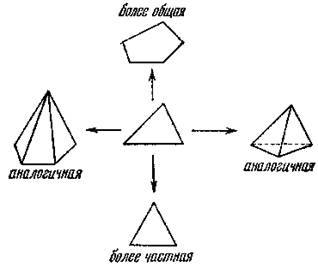
Рис. 2. 2. Обобщение, специализация, аналогия.

5. Обобщение, специализация и аналогия часто сотрудничают в решении математических задач[⑬]). Возьмем в качестве примера доказательство наиболее известной теоремы элементарной математики, теоремы Пифагора. Доказательство, которое мы изложим, не является новым. Оно принадлежит самому Евклиду (Евклид IV, 31)

(1) Рассмотрим прямоугольный треугольник со сторонами a, b и c, из которых первая, a, является гипотенузой. Мы хотим доказать, что

a² = b² + c² (A)

38

Эта цель наталкивает нас на мысль построить на трех сторонах нашего треугольника квадраты. И таким образом мы приходим к довольно знакомой части I нашей составной фигуры (рис. 2.3). (Читатель должен вычерчивать части этой фигуры по мере того, как они появляются в нашем рассуждении, чтобы видеть, как она возникает.)

(2) Открытия, даже очень скромные открытия, требуют, чтобы что-то было подмечено, осознана какая-то связь. Мы сумеем открыть доказательство, которое будет приведено ниже, если заметим аналогию между знакомой[6] частью I нашей составной фигуры и едва ли менее знакомой частью II: тот же самый прямоугольный треугольник, что и в I, разбивается в II на две части высотой, опущенной на гипотенузу.

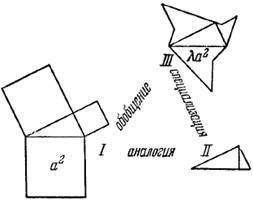
Рис. 2.3.

(3) Возможно, вы не улавливаете аналогии между I и II. Эта аналогия, однако, может быть сделана ясной с помощью совместного обобщения фигур I и II, выраженного в III. Там мы снова находим тот же самый прямоугольный треугольник, и на трех его сторонах построены три многоугольника, подобные друг другу, но в остальном произвольные.

(4) Площадь квадрата, построенного на гипотенузе в I, равна a². Площадь неправильного многоугольника, построенного на гипотенузе в III, можно считать равной λa², множитель λ определяется как отношение двух данных площадей. Но тогда из подобия трех многоугольников, построенных на сторонах a, b и c треугольника в III, следует, что их площади соответственно равны λa², λb², и λc².

Теперь, если бы уравнение (A) было верно (как устанавливается теоремой, которую мы хотим доказать), то было бы верно также и следующее:

λa² = λb² + λc² (B)

Действительно, нужно лишь очень небольшое применение алгебры, чтобы из (A) вывести (B). Теперь (B) представляет обобщение исходной теоремы Пифагора: если три подобных многоугольника построены на трех сторонах прямоугольного треугольника, то многоугольник, построенный на гипотенузе, равен по площади сумме двух других.

Поучительно заметить, что это обобщение равносильно частному случаю, от которого мы отправлялись. В самом деле, мы можем

39

уравнения (A) и (B) вывести одно из другого путем умножения или деления на λ (которое как отношение двух площадей отлично от 0).

(5) Общая теорема, выраженная в (B), равносильна не только частному случаю (A), но и любому другому частному случаю. Следовательно, если бы какой-нибудь такой частный случай оказался очевидным, то общий случай был бы доказан.

Так вот, пытаясь найти полезную специализацию, поищем подходящий частный случай. И действительно, II представляет такой случай. В самом деле, прямоугольный треугольник, построенный на своей собственной гипотенузе, как хорошо известно и как легко видеть, подобен двум другим треугольникам, построенным на его катетах. И, очевидно, площадь всего треугольника равна сумме площадей двух его частей. Таким образом, теорема Пифагора доказана.

Предыдущее рассуждение чрезвычайно поучительно. Случай является поучительным, если мы можем научиться на нем чему-нибудь, приложимому к другим случаям, и тем более поучительным, чем шире границы возможных приложений. И вот на предыдущем примере мы можем научиться употреблению таких фундаментальных мыслительных операций, как обобщение, специализация и восприятие аналогий. Возможно, не существует открытий ни в элементарной, ни в высшей математике, ни даже, пожалуй, в любой другой области, которые могли бы быть сделаны без этих операций, в особенности без аналогии.

Предыдущий пример показывает, как от частного случая (от случая, представленного фигурой I) с помощью обобщения мы можем подняться к более общей ситуации (к фигуре III) и с помощью специализации вновь спуститься отсюда к аналогичному случаю (к фигуре II). Он демонстрирует также тот факт, столь обычный в математике и тем не менее столь поражающий начинающего или философа, хотя он как будто и знает, что общий случай может быть логически равен частному случаю. Наш пример просто и наглядно показывает, как обобщение, специализация и аналогия естественно сочетаются в усилии достигнуть желаемого решения. Заметьте, что, для того чтобы полностью понять предыдущее рассуждение, нужен лишь минимум предварительных знаний.

6. Открытие по аналогии. Аналогия, по-видимому, имеет долю во всех открытиях, но в некоторых она имеет львиную долю. Я хочу проиллюстрировать это примером, не совсем элементарным, но имеющим исторический интерес и производящим значительно более сильное впечатление, чем любой вполне элементарный пример, который я могу себе представить.

Яков Бернулли, швейцарский математик (1654—1705), современник Ньютона и Лейбница, открыл суммы нескольких бесконечных рядов, но ему не удалось найти сумму ряда чисел, обратных

40

квадратам:

«Если кому-либо удастся, — писал Бернулли, — найти то, что до сих пор не поддавалось нашим усилиям, и если он сообщит это нам, то мы будем очень ему обязаны».

Эта задача привлекла внимание другого швейцарского математика, Леонарда Эйлера[⑭] (1707—1783), который родился, как и Яков Бернулли, в Базеле и был учеником Иоганна Бернулли (1667—1748), брата Якова. Он нашел различные выражения для искомой суммы (определенные интегралы, другие ряды), но ни одно из них его не удовлетворяло. одним из этих выражений он воспользовался, чтобы вычислить сумму с точностью до семи знаков (1,644934). Но это только приближенное значение, а его целью было найти точное. В конце концов он открыл его. Аналогия привела его к чрезвычайно дерзкому предположению.

(1) Начнем с обозрения нескольких элементарных алгебраических фактов, существенных в открытии Эйлера. Если уравнение n-й степени

a₀ + a₁x + a₂x² + … + a_nxⁿ = 0

имеет n различных корней

α₁, α₂, …, α_n,

то многочлен, стоящий в его левой части, может быть представлен как произведение n линейных множителей

a₀ + a₁x + a₂x² + … + a_nxⁿ = a_n(x—α₁) (x—α₂) … (x—α_n)

Сравнивая члены с одной и той же степенью x в обеих частях этого тождества, выводим хорошо известные соотношения между корнями и коэффициентами уравнения, простейшим из которых является

a_n—1 = — a_n (α₁ + α₂ + … + α_n);

мы находим его, сравнивая члены с x^n—1.

Разложение на линейные множители можно представить по-другому. Если ни один из корней α_1, α_2, …, α_n не равен 0 или (что то же самое) если α₀ отлично от нуля, то мы имеем также

и

41

Существует еще другой вариант. Предположим, что уравнение степени 2n имеет вид

b₀ — b₁x² + b₂x⁴ — … + (—1)ⁿb_nx²ⁿ = 0

и 2n различных корней

β₁, –β₁, β₂, –β₂, …, β_n, –β_n.

Тогда

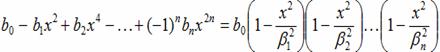
(2) Эйлер рассматривает уравнение

sin x = 0,

или

Левая часть имеет бесконечное число членов, она «бесконечной степени». Поэтому не удивительно, говорит Эйлер, что имеется бесконечное число корней

0, π, –π, 2π, –2π, 3π, –3π, …

Эйлер отбрасывает корень 0. Он делит левую часть уравнения на x, линейный множитель, соответствующий корню 0, и получает таким образом уравнение

с корнями

π, – π, 2π, –2π, 3π, –3π, …

Мы встречались с аналогичной ситуацией раньше, в (1), когда рассматривали последний вариант разложения на линейные множители. Эйлер по аналогии заключает, что

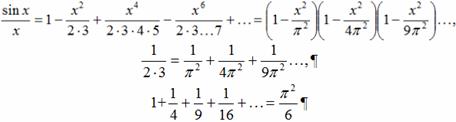
42

Это тот самый ряд, который не поддавался усилиям Якова Бернулли, но это было дерзкое заключение.

(3) Эйлер очень хорошо знал, что его заключение было дерзким. «Метод был новым и никогда еще не использовался для такой цели», — писал он десять лет спустя. Он сам видел некоторые возражения и многие возражения были выдвинуты его друзьями-математиками, когда они оправились после первого восхищенного изумления.

Однако у Эйлера были свои основания верить в это открытие.

Прежде всего, числовое значение для суммы ряда, которое он вычислял раньше, до последнего знака согласовалось с π²/6. Сравнивая следующие коэффициенты в его выражении sin x в виде произведения, он нашел сумму другого замечательного ряда, а именно ряда чисел, обратных четвертым степеням:

Снова он исследовал числовое значение и снова нашел согласие.

(4) Эйлер испытал свой метод и на других примерах. Ему удалось при этом вновь получить сумму π²/6 для ряда Якова Бернулли с помощью различных видоизменений своего первого подхода. Ему удалось также заново открыть своим методом сумму важного ряда, принадлежащего Лейбницу.

Остановимся на последнем вопросе. Рассмотрим, следуя Эйлеру, уравнение

1 — sin x = 0.

Оно имеет корни

Каждый из этих корней является, однако, двойным корнем. (Кривая y = sin x не пересекает при этих абсциссах прямую y = 1, а касается ее. Производная левой части, но не вторая производная при этих значениях x обращается в нуль.) Следовательно, уравнение

имеет корни

и заключение Эйлера по аналогии приводит к разложению на линейные множители:

43

Сравнивая коэффициенты при ч в обеих частях равенства, получаем

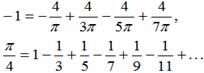
Это — знаменитый ряд Лейбница; дерзкий прием Эйлера привел к уже известному результату. «Для нашего метода, — говорит Эйлер, — который может некоторым казаться недостаточно надежным, здесь обнаруживается великое подтверждение. Поэтому мы вообще не должны сомневаться в других результатах, выведенных тем же методом».

(5) Однако Эйлер продолжал сомневаться. Он и дальше производил числовые проверки, описанные выше в (3), исследовал все больше рядов и все больше десятичных знаков и во всех подвергавшихся исследованию случаях находил согласие. Он испытывал и другие подходы, и наконец ему удалось не только приближенно, но и точно подтвердить значение π²/6 для суммы ряда Якова Бернулли. Он нашел новое доказательство. Это доказательство, хотя и скрытое и остроумное, опиралось на более обычные соображения и было принято как совершенно строгое. Итак, наиболее бросающееся в глаза следствие открытия Эйлера было убедительно подтверждено. Эти доводы, по-видимому, убедили Эйлера в том, что его результат правилен[⑮].

7. Аналогия и индукция. Мы хотим узнать что-нибудь о природе изобретательных и индуктивных рассуждений. Что мы можем почерпнуть из только что приведенного рассказа?

(1) Решающий шаг Эйлера был дерзким. С точки зрения строгой логики он был явной ошибкой: Эйлер применил правило к такому случаю, для которого правило не было остановлено; правило, относящееся к алгебраическим уравнениям, он применил к уравнениям неалгебраическим. С точки зрения строгой логики шаг Эйлера не был оправдан. Однако он был оправдан аналогией, аналогией с наиболее плодотворными достижениями растущей науки, которую через несколько лет он сам назвал «Анализом Бесконечного». Другие

44

математики, до Эйлера, переходили от конечных разностей к бесконечно малым разностям, от сумм с конечным числом членов к суммам с бесконечным числом членов, от конечных произведений к бесконечным произведениям. И таким же образом Эйлер перешел от уравнений конечной степени (алгебраических уравнений) к уравнениям бесконечной степени, применяя к бесконечному правила, установленные для конечного.

Эта аналогия, этот переход от конечного к бесконечному окружен ловушками. Как избежал их Эйлер? Он был гением, ответят некоторые, и, конечно, это вовсе не объяснение. Эйлер имел серьезные основания верить в свое открытие. Имея хоть сколько-нибудь здравого смысла, мы сможем понять эти основания без сверхъестественной проницательности, свойственной гениям.

(2) Основания Эйлера для веры в это открытие, кратко изложенные выше[⑯]), не являются доказательными. Эйлер не возвращается к исследованию оснований своего предположения[⑰], своего дерзкого перехода от конечного к бесконечному; он только изучает его следствия. Он рассматривает подтверждение любого такого следствия как аргумент в пользу своего предположения. Он принимает и приближенные, и точные подтверждения, но, по-видимому, придает больше веса последним. Он изучает также следствия тесно связанных аналогичных предположений[⑱] и рассматривает подтверждение такого следствия как аргумент в пользу своего предположения.

Основания Эйлера в действительности были индуктивными. Изучение следствий предположения и оценка его на основе такого изучения — это типичный индуктивный прием. В научном исследовании, как и в обычной жизни, мы верим или должны были бы верить в предположение больше или меньше в соответствии с тем, лучше или хуже его обозримые следствия согласуются с фактами

Короче говоря, Эйлер, по-видимому, рассуждает таким же образом, как обычно рассуждают разумные люди, ученые или неученые. Он, по-видимому, принимает некоторые принципы:

Предположение становится более правдоподобным после подтверждения любого нового следствия.

И:

Предположение становится более правдоподобным, если становится более правдоподобным аналогичное предположение.

Не этого ли рода принципы лежат в основе процесса индукции?

45

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ II

Первая часть

1. Правильное обобщение.

A. Найдите три числа x, y и z, удовлетворяющие следующей системе уравнений

9x — 6y — 10z = 1,

—6x + 4y + 7z = 0,

x² — y² — z² = 9.

Если вам нужно решить A, то какое из следующих обобщений может лучше способствовать решению: B, C или D?

B. Найдите три неизвестных из системы трех уравнений.

C. Найдите три неизвестных из системы трех уравнений, первые два из которых линейны, а третье второй степени.

D. Найдите n неизвестных из системы n уравнений, первые n — 1 из которых линейны.

2. Даны произвольно расположенные точка и «правильная» пирамида с шестиугольным основанием. (Пирамида называется «правильной», если ее основание есть правильный многоугольник, через центр которого проходит высота пирамиды.) Найдите плоскость, которая проходит через данную точку и делит пополам объем данной пирамиды.

Чтобы помочь вам, я задаю вопрос: Каково правильное обобщение?

3. A. Три прямые, не лежащие в одной плоскости, проходят через одну и ту же точку O. Проведите через O плоскость, одинаково наклоненную к этим трем прямым.

B. Три прямые, не лежащие в одной плоскости, проходят через одну и ту же точку. Точка P находится на одной из этих прямых; проведите через P плоскость, одинаково наклоненную к этим трем прямым.

Сравните задачи A и B. Могли бы вы воспользоваться решением одной при решении другой? В чем состоит их логическая связь?

4. A. Вычислите интеграл

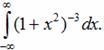
B. Вычислите интеграл

где p — данное положительное число.

Сравните задачи A и B. Могли бы вы воспользоваться решением одной при решении другой? В чем состоит их логическая связь?

5. Крайний частный случай. Два человека сидят за столом обычной прямоугольной формы. Один кладет на стол свой пенс, затем то же делает другой и так далее, поочередно. Подразумевается, что каждый пенс лежит на столе своей плоскостью и не налегает на какую-нибудь ранее положенную монету. Тот игрок, который кладет на стол последнюю монету, забирает деньги. Какой из игроков должен выиграть, если каждый играет наилучшим образом?

Это старинная, но превосходная головоломка. Мне довелось однажды наблюдать за действительно выдающимся математиком, когда ему была предложена эта головоломка. Он начал с того, что сказал: «Допустим, что стол так мал, что он покрывается одним пенсом. Тогда, очевидно, должен выиграть первый игрок. Иными словами, он начал с рассмотрения крайнего частного случая, в котором решение очевидно.

Из этого частного случая вы можете получить полное решение, если представите себе стол постепенно расширяющимся и смещающим все больше и больше монет. Может быть, еще лучше обобщить задачу и подумать о столах

46

различных форм и размеров. Если вы подметите, что стол имеет центр симметрии и что правильное обобщение могло бы состоять в рассмотрении столов с центром симметрии, то получите решение или по крайней мере окажетесь к нему очень близко.

6. Постройте общую касательную двух данных окружностей.

Чтобы помочь вам, я задаю вопрос: Существует ли более доступный крайний частный случай?

7. Ведущий частный случай. Площадь многоугольника равна A, его плоскость образует с другой плоскостью угол α. Многоугольник ортогонально проектируется на вторую плоскость. Найдите площадь проекции.

Существует одна форма, с которой особенно легко иметь дело: прямоугольник, основание которого параллельно линии l пересечения плоскости проектируемой фигуры с плоскостью проекции. Если a — основание такого прямоугольника, b — его высота и, следовательно, его площадь ab, то соответствующие величины для проекции будут a, b cos α и ab cos α. Если площадь такого прямоугольника равна A, то площадь его проекции равна A cos α.

Этот частный случай прямоугольника с основанием, параллельным l, не только особенно доступен; он является ведущим частным случаем. Другие случаи следуют из него; решение задачи в ведущем частном случае включает в себя решение задачи в общем случае. Действительно, отправляясь от прямоугольника с основанием, параллельным l, мы можем распространить правило «площадь проекции равна A cos α» последовательно на все другие фигуры. Сначала на прямоугольные треугольники с катетом, параллельным l (разбивая на две равные части тот прямоугольник, с которого мы начали). Затем на любой треугольник со стороной, параллельной l (соединяя два прямоугольных треугольника); наконец, на произвольный многоугольник (разбивая его на треугольники только что упомянутого вида). Мы можем даже перейти к фигурам с криволинейными границами (рассматривая их как пределы многоугольников).

8. Угол с вершиной в центре круга вдвое больше угла с вершиной на окружности, опирающегося на то же основание, т. е. на ту же дугу. (Евклид III, 20).

Если дан угол с вершиной в центре, то угол с вершиной на окружности еще не определен, его вершина может иметь различные положения. Каким является «ведущее частное положение» в обычном доказательстве теоремы (доказательстве Евклида)?

9. Основная в теории аналитических функций теорема Коши утверждает, что интеграл от функции комплексного переменного вдоль произвольной замкнутой кривой равен нулю, если в области, ограниченной этой кривой, функция регулярна. Мы можем рассмотреть частный случай теоремы Коши, когда замкнутая кривая есть треугольник, как ведущий частный случай: доказав теорему для треугольника, мы легко сумеем последовательно распространить ее на многоугольники (соединяя треугольники) и кривые (рассматривая их как пределы многоугольников). Обратите внимание на аналогию с задачами 7 и 8.

10. Частный случай-представитель. Вам нужно решить какую-нибудь задачу о многоугольниках с n сторонами. Вы чертите пятиугольник, решаете задачу для него, изучаете ваше решение и замечаете, что оно в такой же мере годится в общем случае для любого n, как и в частном случае n = 5. Тогда вы можете назвать n = 5 частным случаем-представителем: он представляет вам общий случай. Конечно, для того чтобы быть действительно представителем, случай n = 5 не должен иметь никаких специфических упрощений, которые могли бы ввести вас в заблуждение. Частный случай-представитель должен быть не проще, чем общий случай.

47

Частные случаи-представители часто удобны в преподавании. Мы можем доказать теорему об определителях n-го порядка, тщательно рассматривая определители всего лишь 3-го порядка.

11. Аналогичный случай. Задача состоит в проектировании самолетов так, чтобы опасность перелома черепа в случае аварии была наименьшей. Врач, изучающий эту задачу, экспериментирует с яйцами, разбивая их при различных условиях. Что он делает? Он видоизменил первоначальную задачу и изучает теперь вспомогательную задачу разбивания яиц вместо разбивания черепов. Связь между двумя задачами — первоначальной и вспомогательной — аналогия. С механической точки зрения голова человека и куриное яйцо в общих чертах аналогичны: голова и яйцо состоят из жесткой хрупкой оболочки, содержащей студенистое вещество.

12. Если две прямые в пространстве пересекаются тремя параллельными плоскостями, то соответствующие отрезки пропорциональны.

Чтобы помочь вам найти доказательство, я задаю вопрос: Существует ли более простая теорема?

13. Четыре диагонали параллелепипеда имеют общую точку, являющуюся серединой каждой из них.

Существует ли более простая аналогичная теорема?

14. Сумма любых двух плоских углов трехгранного угла больше, чем третий плоский угол.

Существует ли более простая аналогичная теорема?

15. Рассмотрите тетраэдр как тело, аналогичное треугольнику. Перечислите понятия пространственной геометрии, аналогичные следующим понятиям плоской геометрии: биссектрисы трех углов треугольника пересекаются в одной точке, являющейся центром окружности, вписанной в треугольник[7].

16. Рассмотрите пирамиду как тело, аналогичное треугольнику. Перечислите тела, аналогичные следующим плоским фигурам: параллелограмм, прямоугольник, квадрат, биссектриса угла. Сформулируйте теорему пространственной геометрии, аналогичную следующей теореме плоской геометрии: площадь круга равна площади треугольника, основание которого имеет ту же длину, что и окружность, и высота которого равна радиусу.

17. Придумайте теорему пространственной геометрии, аналогичную следующей теореме плоской геометрии: высота равнобедренного треугольника проходит через середину основания.

Какой пространственное тело вы рассматриваете как аналогичное равнобедренному треугольнику?

18. Великие аналогии. (1) Предыдущие примеры 12—17 подчеркивают аналогию между плоской и пространственной геометрией эту аналогию можно рассматривать со многих точек зрения и поэтому часто она неоднозначна и не всегда имеет ясные очертания, но она является неисчерпаемым источником новых идей и новых открытий.

(2) Числа и фигуры являются не единственными объектами математики. Математика принципиально неотделима от логики и имеет дело со всеми объектами, которые могут быть объектами точной теории[⑲]. Числа и фигуры,

48

однако, являются наиболее обычными объектами математики, и математики любят иллюстрировать факты, касающиеся чисел, свойствами фигур, а факты, касающиеся фигур, свойствами чисел. Поэтому существуют бесчисленные виды аналогии между числами и фигурами. Некоторые из этих видов очень ясны. Так в аналитической геометрии мы изучаем точно определенное соответствие между алгебраическими и геометрическими объектами и отношениями. Но многообразие геометрических фигур неисчерпаемо, как неисчерпаемо и многообразие возможных операций над числами; столь же неисчерпаемы и возможные соответствия между этими многообразиями.

(3) Изучение пределов и предельных процессов вводит иной вид аналогии, которую можно назвать аналогией между бесконечным и конечным. Так бесконечные ряды и интегралы в различных отношениях аналогичны конечным сумма, пределами которых они являются; дифференциальное исчисление аналогично исчислению конечных разностей; дифференциальные уравнения, особенно линейные однородные уравнения, до некоторой степени аналогичны алгебраическим уравнениям и так далее. Важной относительно новой ветвью математики является теория интегральных уравнений; она дает удивительный и прекрасный ответ на вопрос: что в интегральном исчислении является аналогом системы n линейных уравнений с n неизвестными? Аналогия между бесконечным и конечным вызывает особый интерес потому, что она имеет своеобразные трудности и ловушки. Она может вести к открытию или к ошибке; см. пример 46.

(4) Галилей, открывший параболическую траекторию брошенных тел и количественный закон их движения, сделал также великие открытия в астрономии. С помощью своего только что изобретенного телескопа он открыл спутников Юпитера[8]. Он заметил, что эти спутники, обращающиеся вокруг планеты Юпитер, аналогичны Луне, обращающейся вокруг Земли, а также аналогичны планетам, обращающимся вокруг Солнца. Он открыл также фазы Венеры и подметил их сходство с фазами Луны. Эти открытия, воспринятые как великое подтверждение гелиоцентрической теории Коперника, горячо обсуждались в то время. Странно, что Галилей не заметил аналогии между движением небесных тел и движением брошенных тел, которую вполне возможно осознать интуитивно. Траектория брошенного тела обращена своей вогнутостью к земле, и то же самое имеет место для траектории Луны. Ньютон настаивал на этой аналогии: «брошенный камень под действием собственного веса отклоняется от прямолинейного пути, по которому он должен был бы следовать под влиянием только начального броска, и вынужден описать кривую линию в воздухе, и …наконец упасть на землю; и чем больше скорость, с которой он брошен, тем дальше он пролетит, прежде чем упадет на землю. Поэтому мы можем предположить, что при соответственно возрастающей скорости он опишет дуги в 1, 2, 5, 10, 100, 1000 миль, прежде чем упадет на землю, пока наконец, покинув пределы Земли, он не должен будет перейти в пространство, не коснувшись ее»[⑳]. См. рис 2.4.

Меняясь непрерывно, траектория камня переходит в траекторию Луны. И как камни и Луна связаны с Землей, так спутники Юпитера связаны с Юпитером или Венера или другие планеты с Солнцем. Без ясного понимания этой аналогии мы можем только очень несовершенно понять открытие Ньютоном всемирного тяготения, которое до сих пор мы можем рассматривать как величайшее когда бы то ни было сделанное научное открытие.

19. Выяснение аналогии. Аналогия часто является смутной. Ответ на вопрос, что чему аналогично, часто неоднозначен. Смутность аналогии не уменьшает ее интереса и полезности; однако те случаи, когда понятие аналогии

49

достигает ясности логических или математических понятий, заслуживают специального рассмотрения.

(1) Аналогия есть сходство отношений. Это сходство имеет ясный смысл, если отношения управляются одними и теми же законами. С этой точки зрения сложение чисел аналогично умножению чисел в той степени, в какой

Рис. 2.4. От траектории камня к траектории Луны. Из «Системы мира» Ньютона.

сложение и умножение подчиняется одним и тем же правилам. И сложение и умножение коммутативны и ассоциативны,

a + b = b + a, ab = ba,

(a + b) + c = a + (b + c), (ab)c = a(bc).

Сходны, поскольку каждое из них допускает решение и не более чем одно решение. (Чтобы иметь возможность установить последнее правило без исключения, мы должны допустить отрицательные числа при рассмотрении сложения и исключить случай a = 0 при рассмотрении умножения.) В этой связи вычитание аналогично делению; действительно, решениями вышеуказанных уравнений соответственно являются

50

Далее, число 0 аналогично числу 1; действительно, прибавление 0 к любому числу, как и умножение любого числа на 1, не меняет этого числа,

a + 0 = a, a·1 = a.

Эти законы — одни и те же для различных классов чисел; мы можем рассматривать здесь рациональные числа, или действительные числа, или комплексные числа. Вообще, системы объектов, подчиняющиеся одним и тем же основным законам (или аксиомам), можно рассматривать как аналогичные между собой, и этот вид аналогии имеет вполне ясный смысл.

(2) Сложение действительных чисел аналогично умножения положительных чисел еще и в другом смысле. Любое действительное число r есть логарифм некоторого положительного числа p,

r = log p,

(Если мы рассматриваем десятичные логарифмы, то r = — 2 при p = 0,01.) В силу этого соотношения каждому положительному числу соответствует совершенно определенное действительное число, и каждому действительному числу — совершенно определенное положительное число. При этолм соответствии сложение действительных чисел соответствует умножению положительных чисел. Если

r = log p, r' = log p', r" = log p",

то любое из следующих двух соотношений влечет за собой другое:

r + r' = r", pp' = p".

Формула слева и формула справа рассказывают один и тот же рассказ на двух разных языках. Назовем одно из соответствующих чисел переводом другого; например, назовем действительное число r (логарифм p) переводом p, а p оригиналом для r. (Мы могли бы поменять местами слова «перевод» и «оригинал», но должны были сделать выбор, и после этого мы придерживаемся нашего выбора.) В этой терминологии сложение выступает как перевод умножения, вычитание — как перевод деления, 0 — как перевод 1, коммутативный закон и ассоциативный закон для сложения действительных чисел понимаются как переводы этих законов для умножения положительных чисел. Перевод, конечно отличается от оригинала, но он является правильным переводом в следующем смысле: из любого соотношения между элементами оригинала мы можем с непреложностью вывести соответствующее соотношение между соответствующими элементами перевода и наоборот. Такой правильные перевод, т. е. взаимно однозначное соответствие, сохраняющее законы некоторых соотношений, на техническом языке математика называется изоморфизмом. Изоморфизм есть вполне выясненный вид аналогии.

(3) Третий тип вполне выясненной аналогии есть то, что математики называют на техническом языке гомоморфизмом (или многозначным изоморфизмом). Подробное изложение примера или точное описание этого понятия заняло бы слишком много времени, но мы можем попытаться понять следующее приближенное описание. Гомоморфизм есть своего рода систематически сокращенный перевод. Оригинал не только переводится на другой язык, но и сокращается, так что то, что получается в конечном счете после перевода и сокращения, оказывается систематически равномерно сжатым в половину или одну треть или в какую-либо другую долю первоначальной протяженности. Тонкости при таком сокращении могут быть потеряны но все, что есть в оригинале, чем-то представлено в переводе, и в уменьшенном масштабе соотношения сохраняются.

20. Цитаты.

«Посмотрим, не могли бы мы удачно придумать какую-либо другую общую задачу, которая содержит первоначальную задачу и легче поддается решению. Так, когда мы разыскиваем касательную в данной точке, мы представляем себе, что просто разыскиваем прямую, пересекающую данную кривую

51

в данной точке и в некоторой другой точке, удаленной на данное расстояние от данной точки. После решения этой задачи, которую всегда можно легко решить с помощью алгебры, мы находим касательную как частный случай, именно частный случай, когда данное расстояние минимально, сводится к точке, исчезает» (Лейбниц).

«Как часто случается, общая задача оказывается легче, чем была бы частная задача, если бы мы пытались решить ее непосредственно, в лоб» (Лежен-Дирихле, Дедекинд).

«[Может оказаться полезным] свести род ко всем его отдельным видам, и таким образом к немногим видам, однако наиболее полезно свести род к одному наименьшему виду» (Лейбниц).

«Правильно в философии рассматривать сходство, даже в вещах, далеко отстоящих друг от друга» (Аристотель).

«Сравнения имеют огромное значение, поскольку они сводят неизвестные отношения к известным отношениям.

Правильное понимание есть, наконец, схватывание отношений (un saisir de rapports). Но мы понимаем отношения более отчетливо и более ясно, когда осознаем, что они одни и те же в широко отличающихся случаях и между совершенно разнородными объектами (Шопенгауэр).

Вам не следует, однако забывать, что существует два рода обобщений: один дешевый, а другой ценный. Легко обобщить путем разрежения, важно обобщить путем сгущения. Развести немного вина большим количеством воды дешево и легко. Приготовить очищенный и сгущенный экстракт из некоторых хороших составных частей значительно труднее, но ценно. Обобщение путем сгущения сжимает в одно понятие большого размаха несколько идей, казавшихся ранее разбросанными. Так, теория групп сводит к общему выражению идеи, рассеянные перед тем в алгебре, теории чисел, анализе, геометрии, кристаллографии и других областях. В настоящие дни более моден, чем прежде, другой род обобщения. Он разводит маленькие идеи большой терминологией. Автор обычно предпочитает даже эти маленькие идеи брать у кого-либо другого, воздерживаясь от добавления какого-либо собственного наблюдения, и избегает решения каких-либо задач, за исключением нескольких задач, возникающих из трудностей его собственной терминологии. Было бы очень легко привести пример, но я не хочу наживать врагов[21][9].

Вторая часть

Все примеры и примечания этой второй части связаны с § 6 и между собой. Многие из них прямо или косвенно ссылаются на пример 21, который следует прочитать вначале.

21. Предположение Э. Мы рассматриваем равенство

как предположение; мы называем его «предположением Э». Следуя Эйлеру, мы хотим исследовать это предположение индуктивно.

Индуктивное исследование предположения включает в себя сопоставление его следствий с фактами. Мы часто будем «предсказывать, исходя из Э, и подтверждать». «Предсказание», исходя из Э» означает выведение в предположении, что Э верно. «Подтверждение означает выведение без этого предположения. Факт «находится в согласии с Э», если он (легко) может быть выведен из предположения, что Э верно.

52

В дальнейшем мы будем считать известными элементы математического анализа (которые, с формальной точки зрения, были полностью известны Эйлеру во время его открытия), включая строгое понятие предела (относительно которого Эйлер никогда не достигал полной ясности). Мы будем пользоваться только такими предельными процессами, которые могут быть оправданы (большая часть из них совсем легко), но не будем входить в детали оправданий.

22. Мы знаем, что sin (– x) = –sin x. Находится ли этот факт в согласии Э?

23. Предскажите, исходя из Э, и подтвердите значение бесконечного произведения

24. Предскажите, исходя из Э, и подтвердите значение бесконечного произведения

25. Сравните примеры 23 и 24 и сделайте обобщение.

26. Предскажите, исходя из Э, значение бесконечного произведения

27. Покажите, что предположение Э равносильно утверждению

28. Мы знаем, что sin (x +π) = –sin x. Находится ли этот факт в согласии с Э?

29. Метод § 6 (2) приводит к предположению

Покажите, что это не только аналог, но и следствие предположения Э.

30. Мы знаем, что

Находится ли этот факт в согласии с Э?

31. Предскажите, исходя из Э, и подтвердите значение бесконечного произведения

32. Предскажите, исходя из Э, и подтвердите значение бесконечного произведения

33. Сравните примеры 31 и 32 и сделайте обобщение.

34. Мы знаем, что cos (–x) = cos x. Находится ли этот факт в согласии с Э?

35. Мы знаем, что cos (x + π) = –cos x. Находится ли этот факт в согласии с Э?

36. Выведите из Э произведение для 1 –sin x, предположение о котором мы сделали в § 6 (4).

53

37. Выведите из Э, что

38. Выведите из Э, что

и найдите суммы бесконечных рядов, появляющихся в качестве коэффициентов в правой части.

39. Выведите из Э, что

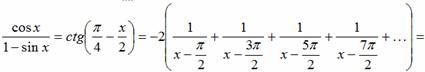
и найдите суммы бесконечных рядов, появляющихся в качестве коэффициентов в последнем выражении.

40. Покажите, что

откуда получается второй вывод для суммы ряда в левой части равенства.

41. (продолжение). Попытайтесь найти третий вывод, зная, что

и что для n = 0, 1, 2, …

42. (продолжение). Попытайтесь найти четвертый вывод, зная, что

54

и что для n = 0, 1, 2, …

43. Эйлер (Opera Omnia, ser. 1, vol. 14, p. 40, 41) пользовался формулой

справедливой для 0 < x < 1, чтобы численно найти сумму ряда в левой части.

(a) Докажите эту формулу.

(b) Какое значение x наиболее выгодно для вычисления суммы ряда, стоящего в левой части?

44. Возражение и первый шаг к доказательству. Нет оснований a priori допускать, что sin x может быть разложен на линейные множители, соответствующие корням уравнения

sin x = 0.

Но если бы даже мы допустили это, остается возражение: Эйлер не доказал, что

0, π, – π, 2π, –2π, 3π, –3π, …

— все корни этого уравнения. Мы можем убедиться (рассматривая кривую y = sin x), что нет других действительных корней, однако Эйлер никоим образом не исключил возможность существования комплексных корней.

Это возражение было выдвинуто Даниилом Бернулли (сыном Иоганна, 1700—1788). Эйлер ответил на это рассмотрением

где

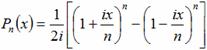
есть многочлен (степени n, если n нечетное).

Покажите, что P_n не имеет комплексных корней.

45. Второй шаг к доказательству. Предполагая, что n в примере 44 нечетно, разложите P_n(x)/x на множители так, чтобы его k-й множитель для каждого фиксированного k (k = 1, 2, 3, …) приближался к

когда n стремится к ∞

46. Опасности аналогии. Коротко говоря, аналогия между конечным и бесконечным привела Эйлера к великому открытия. Однако его путь проходил по самому краю возможной ошибки. Вот пример, показывающий опасность в задаче меньшего масштаба.

Ряд

сходится. Его сумма l грубо может быть оценена с помощью первых двух

55

членов:

Теперь,

В этом ряде существует всего один член с данным четным знаменателем (он отрицателен), но два члена сданным нечетным знаменателем (один положительный, а другой отрицательный). Соединим вместе члены с одним и тем же нечетным знаменателем

Но 2l ≠ l потому, что l ≠ 0. Где ошибка и как можно предохранять себя от ее повторения?

III. ИНДУКЦИЯ В ПРОСТРАНСТВЕННОЙ ГЕОМЕТРИИ

В самой математике главные средства достигнуть истины — индукция и аналогия. — Лаплас[22]

1. Многогранники. «Сложный многогранник имеет много граней, углов и ребер». Какое-нибудь туманное замечание такого рода легко приходит в голову почти всякому, кто имел какое-либо соприкосновение с пространственной геометрией. Не так много людей, однако, захотят сделать серьезное усилие, чтобы углубиться в это замечание и отыскать за ним какую-нибудь более точную информацию. Правильно было бы ясно различить участвующие величины и задать какой-нибудь определенный вопрос. Обозначим поэтому число граней, число вершин и число ребер многогранника соответственно через Г, В и Р (начальные буквы соответствующих слов) и поставим такой четкий вопрос: «Всегда ли верно, что число граней возрастает, когда возрастает число вершин? Непременно ли Г возрастает вместе с В?»

Для начала мы едва ли можем сделать что-либо лучшее, чем исследовать примеры, конкретные многогранники. Так, для куба (тело I на рис. 3.1)

Г = 6, В = 8, Р = 12.

Или для призмы с треугольным основанием (тело II на рис. 3.1)

Г = 5, В = 6, Р = 92.

Раз уж мы выбрали такой путь, нам, естественно, нужно просмотреть и сравнить различные тела, например, те, которые показаны на рис. 3.1. Именно, помимо уже упомянутых I и II, здесь изображены следующие тела: призма с пятиугольным основанием (III), пирамиды с квадратным, треугольным и пятиугольным основаниями (IV, V, VI), октаэдр (VII), «башня с крышей» (VIII, пирамида, поставленная на верхнюю грань куба как на основание) и «усеченный куб» (IX). Сделаем маленькое усилие воображения и представим себе эти тела одно за другим достаточно ясно, чтобы сосчитать грани, вершины и ребра. Найденные числа записаны в следующей таблице:

57

Многогранники		Г	В	Р
I.	куб	6	8	12
II.	трехгранная призма	5	6	9
III.	пятигранная призма	7	10	15
IV.	четырехгранная пирамида	5	5	8
V.	трехгранная пирамида	4	4	6
VI.	пятигранная пирамида	6	6	10
VII.	октаэдр	8	6	12
VIII.	«башня»	9	9	16
IX.	«усеченный куб»	7	10	15

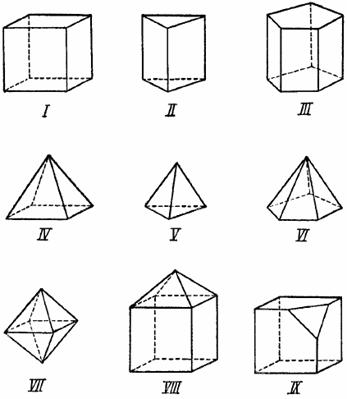
Рис. 3.1. Многогранники.

Наш рис 3.1 имеет некоторое поверхностное сходство с минералогической выставкой, а вышеприведенная таблица до некоторой степени сходна с записной книжкой, в которую физик вносит результаты своих экспериментов. Мы исследуем и сравниваем тела и числа в нашей таблице, как минералог или физик исследовали бы свои с бо́льшим трудом собранные образцы и данные. У нас есть теперь кое-что в руках, чтобы иметь возможность ответить на наш первоначальный вопрос: «Возрастает ли В вместе с Г?» В самом деле, ответ будет «Нет»; сравнивая куб и октаэдр (I и VII), мы видим, что один имеет больше вершин, а другой больше граней.

58

Итак, наша первая попытка установить общую закономерность не удалась.

Мы можем, однако, попробовать что-нибудь другое. Возрастает ли Р вместе с Г? Или с В? Чтобы систематически ответить на эти вопросы, мы перестроим свою таблицу. Запишем наши многогранники в таком порядке, чтобы Р возрастало, когда мы последовательно читаем строки сверху вниз.

Многогранники	Г	В	Р
Трехгранная пирамида	4	4	6
Четырехгранная пирамида	5	5	8
Трехгранная призма	5	6	9
Пятигранная пирамида	6	6	10
Куб	6	8	12
Октаэдр	8	6	12
Пятигранная призма	7	10	15
«Усеченный куб»	7	10	15
«Башня»	9	9	16

Рассматривая наши более удобно расположенные данные, мы легко можем заметить, что никакой закономерности предполагаемого типа не существует. Когда Р возрастает от 15 до 16, В падает от 10 до 9. с другой стороны, когда мы переходим от октаэдра к пятигранной призме, Р возрастает от 12 до 15, но Г падает от 8 до 7. Ни Г, ни В не возрастают вместе с Р по отдельности; это верно, но они, по-видимому, возрастают «в совокупности». Разглядывая свою хорошо составленную таблицу, мы можем подметить, что Г и В возрастают «совместно»: сумма Г + В возрастает, когда мы читаем строки сверху вниз. А затем мы внезапно можем заметить более точную закономерность: во всей таблице

Г + В = Р + 2.

Это соотношение подтверждается во всех девяти случаях, записанных в нашей таблице. Кажется невероятным, чтобы такая упорная закономерность оказалась простым совпадением. Итак, мы пришли а предположению, что не только в наблюдавшихся нами случаях, но и в любом многограннике число граней, увеличенное на число вершин, равно числу ребер, увеличенному на два.

2. Первые подкрепляющие контакты. Натуралист, прошедший хорошую школу, нелегко допускает предположение. Даже если предположение кажется правдоподобным и в нескольких случаях подтвердилось, он будет в нем сомневаться и собирать новые наблюдения или придумывать новые эксперименты, чтобы его проверить.

59

Именно это можем сделать и мы. Мы собираемся исследовать и другие многогранники, подсчитать их грани, вершины и ребра и сравнить Г + В и Р + 2. эти числа могут быть равны или нет. Будет интересно выяснить, что же имеет место в действительности.

Рассматривая рис. 3.1, мы можем заметить, что уже исследовали три из правильных многогранников, куб, тетраэдр и октаэдр (I, V и VII). Исследуем оставшиеся два, икосаэдр и додекаэдр.

Икосаэдр имеет 20 граней, все они треугольники, и, таким образом, Г = 20. 20 треугольников имеют вместе 3 × 20 = 60 сторон, причем каждое ребро икосаэдра является общей стороной двух треугольников. Следовательно, число ребер равно 60/2 = 30 = Р. Аналогично мы можем найти В. Мы знаем, что вокруг каждой из вершин икосаэдра группируется по 5 его граней. 20 треугольников вместе имеют 3 × 20 = 60 углов, причем 5 углов имеют общую вершину. Следовательно, число вершин равно 60/5 = 12 = В.

Додекаэдр имеет 12 граней, все они пятиугольники, причем вокруг каждой вершины группируется по 3 пятиугольника. Отсюда, как и прежде, заключаем, что

Мы можем прибавить к нашей таблице на стр. 58 еще две строки:

Многогранники	Г	В	Р
Икосаэдр	20	12	30
Додекаэдр	12	20	30

Наше предположение, что Г + В = Р + 2, подтверждается в обоих случаях.

3. Еще подкрепляющие контакты. Благодаря предыдущим подтверждениям, наше предположение стало ощутимо более правдоподобным; но доказано ли оно теперь? Никоим образом. В подобной ситуации скрупулезный натуралист чувствовал бы удовлетворение успехом своего эксперимента, но продолжал бы придумывать дальнейшие эксперименты. Какой многогранник следовало бы нам испытать теперь?

Дело в том, что наше предположение к настоящему времени так хорошо подтвердилось, что подтверждение еще в одном только случае лишь немного прибавило бы к нашей уверенности, возможно, так мало, что едва ли стоило бы труда выбирать многогранник и подсчитывать его части. Не могли ли бы мы найти более стоящий путь испытания нашего предположения?

Рассматривая рис. 3.1, мы можем заметить, что все тела в верхнем ряду имеют одинаковую природу: они призмы. Точно так же все тела во втором ряду — пирамиды. Наше предположение верно

60

для трех призм и трех пирамид, изображенных на рис. 3.1; но верно ли оно для всех призм и пирамид?

Если призма имеет n боковых граней, то она имеет всего n + 2 грани, 2 n вершин и 3 n ребер. Пирамида с n боковыми гранями имеет всего n + 1 грань, n + 1 вершину и 2n ребер. Итак, мы можем добавить еще две строки к нашей таблице на стр. 58:

Многогранники	Г	В	Р
Пирамида с n боковыми гранями	n + 1	n + 1	2n
Призма с n боковыми гранями	n + 2	2n	3n

Наше предположение, утверждающее, что Г + В + Р + 2, оказалось верным не только еще для одного или двух многогранников, но для двух бесконечных серий многогранников.

4. Суровое испытание. Последнее замечание значительно увеличивает нашу уверенность в своем предположении, но, конечно, не доказывает его. Что же нам делать? Нужно ли продолжать испытывать дальнейшие частные случаи? Наше предположение, по-видимому, довольно хорошо выдерживает простые испытания. Поэтому нам следовало бы подвергнуть его какому-нибудь суровому, придирчивому испытанию, имеющему хорошие шансы его опровергнуть.

Взглянем снова на нашу коллекцию многогранников (рис. 3.1). Там имеются призмы (I, II, III), пирамиды (IV, V, VI), правильные многогранники (I, V, VII); но мы уже исчерпывающим образом рассмотрели все эти типы тел. Что там есть еще? Рис. 3.1 содержит также «башню» (VIII), которая получается, если к верхнему основанию куба пристроить «крышу». Здесь мы можем ощутить возможность обобщения. Возьмем вместо куба любой многогранник, выберем любую грань этого многогранника и пристроим к ней «крышу». Пусть первоначальный многогранник имел Г граней, В вершин и Р ребер и пусть выбранная его грань имеет n сторон. Мы пристраиваем к этой грани пирамиду с n боковыми гранями и таким образом получается новый многогранник. Сколько граней, вершин и ребер имеет новый многогранник «с крышей»? При этой операции одна грань (выбранная) теряется, а n новых появляются (n боковых граней пирамиды), так что новый многогранник имеет Г — 1 + n граней. Все вершины многогранника принадлежат и новому многограннику, но одна вершина (вершина пирамиды прибавляется, и, таким образом, новый многогранник имеет В + 1 вершину. Все ребра старого многогранника принадлежат и новому, но прибавляется n ребер (боковые ребра пирамиды), и, таким образом, новый многогранник имеет Р + n ребер.

Подведем итог. Первоначальный многогранник имел соответственно Г, В и Р граней, вершин и ребер, тогда как новый мно-

61

гранник с крышей имеет

Г + n — 1, В + 1 и Р + n

частей соответствующего типа. Согласуется ли это с нашим предположением?

Если выполняется соотношение Г + В = Р + 2, то, очевидно соотношение

(Г + n — 1) + (В + 1) = (Р + n) + 2

также выполняется. Иными словами, если оказывается, что наше предположение подтверждается в случае первоначального многогранника, то оно должно подтверждаться и в случае нового многогранника с «крышей». Наше предположение выдерживает «пристройку крыши», и, таким образом, оно прошло действительно очень суровое испытание. Существует неисчерпаемое разнообразие многогранников, которые можно получить из уже исследованных с помощью повторных «пристроек крыши», и мы доказали, что наше предположение для всех верно.

Кстати, последнее тело нашего рис. 3.1, «усеченный куб (IX), открывает путь для аналогичных рассмотрений. Вместо куба «усечем» любой многогранник, отсекая произвольно выбранную вершину. Пусть первоначальный многогранник имеет соответственно

Г, В и Р

Граней, вершин и ребер и пусть n — число ребер, выходящих из выбранной нами вершины. Отсекая эту вершину, мы вводим одну новую грань (имеющую n сторон), n новых ребер, а также n новых вершин, но теряем одну вершину. Подведем итог: новый, «усеченный», многогранник имеет соответственно

Г + 1, В + n — 1 и Р + n

граней, вершин и ребер. Теперь, из

Г + В = Р + 2

Следует

(Г + 1) + (В + n — 1) = (Р + n) + 2

т. е. наше предположение достаточно прочно для того, чтобы выдержать «усечение». Оно прошло еще одно суровое испытание.

Предыдущие замечания естественно рассматривать как очень сильный аргумент в пользу нашего предположения. Мы можем уловить в них даже нечто другое: первый намек на доказательство. Начиная с каких-либо простых многогранников, как тетраэдр или куб, для которых предположение выполняется, мы можем с помощью пристройки крыши и усечения получить огромное разнообразие других многогранников, для которых предположение также выполняется.

62

Сможем ли мы получить все многогранники? Тогда у нас было бы доказательство! Кроме того, могут существовать и другие операции, которые подобно усечению и пристройке крыши сохраняют предполагаемое соотношение.

5. Подтверждения и подтверждения. Процесс мышления опытного натуралиста несущественно отличается от процесса мышления обычного человека, но он более основателен. И обычного человека, и ученого к предположениям приводит несколько наблюдений, и оба они обращают внимание на позднейшие случаи, которые могли бы оказаться в согласии с предположением или нет. Случаи, находящиеся в согласии, делают предположение более вероятным, противоречащие случаи его опровергают, и здесь начинается отличие: обыкновенные люди обычно более склонны разыскивать случаи первого типа, а ученый — случаи второго типа. Причина этого состоит в том, что каждый человек имеет некоторую долю самомнения — как обычный человек, так и ученый, — но разные люди ценят в себе разные качества. М-р Кто-нибудь не любит признаваться даже самому себе, что он ошибся, и поэтому ему не нравятся противоречащие случаи, он их избегает, он даже склонен, когда они встречаются, находить им такое объяснение, из которого бы вытекало, что они предположению не противоречат. Ученый, наоборот, вполне готов признать ошибочное предположение, но он не любит оставлять вопросы нерешенными. И вот случай, находящийся в согласии, вопрос не разрешает, а противоречащий случай разрешает. Ученый, старающийся найти окончательное решение, разыскивает случаи, которые могли бы опровергнуть предположение, и чем больше эта возможность, тем они ему приятнее. Следует отметить важный момент. Если случай, грозивший опровергнуть предположение, в конце концов оказался с ним в согласии, то предположение выходит из испытания значительно окрепшим. Чем больше опасность, тем больше чести; прохождение через наиболее серьезное испытание дает наиболее высокое признание, наиболее сильное экспериментальное подтверждение предположения. Имеются примеры и примеры, подтверждения и подтверждения. Пример, который с большой вероятностью способен опровергнуть предположение, во всяком случае подводит предположение ближе к решению, чем пример, делающий это с меньшей вероятностью и это объясняет предпочтение ученого[10].

Теперь мы можем заняться нашей собственной конкретной задачей и посмотреть, как применить предыдущие замечания к «экспериментальному исследованию многогранников», которые мы предприняли. Каждый новый случай, в котором подтверждается соотношение Г + В = Р + 2, увеличивает уверенность, что это соотношение верно вообще. Однако мы уже устали от однообразной последовательности подтверждений. Случай, мало отличающийся от ранее исследованных

63

случаев, если он находится в согласии с предположением, конечно, увеличивает нашу уверенность, но увеличивает мало. Действительно, мы легко поверим до испытания, что рассматриваемый случай будет вести себя так же, как и предыдущие случаи, от которых он отличается лишь немногим. Мы хотим не только другого подтверждения, но _подтверждения другого типа. В самом деле, вновь просматривая различные фазы нашего исследования (§§ 2, 3 и 4), мы можем заметить, что каждая из них давала такой тип подтверждения, который существенно превосходил полученные ранее. В каждой фазе предположение подтверждалось для более обширного многообразия случаев, чем в предыдущей.

6. Совсем не похожий случай.

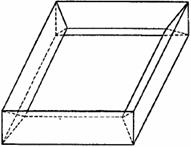
Рис. 3.2. Баранкообразный многогранник.

Поскольку важно разнообразие, поищем какой-нибудь многогранник, совсем не похожий на те, которые мы исследовали до сих пор. Так мы можем напасть на мысль рассмотреть в качестве многогранника раму для картины. Возьмем очень длинный треугольный стержень, отрежем от него четыре куска, приладим эти куски в концах и соединим их в рамообразный многогранник. На рис 3.2 рама положена на стол так, что все ребра, которые уже были на неразрезанном стержне, лежат горизонтально. Имеется 4 раза по 3, т. е. 12 горизонтальных ребер, и также 4 раза по 3 негоризонтальных ребра[11], так что общее число ребер равно Р = 12 + 12 + 24. сосчитав грани и вершины, находим, что Г = 4 × 3 = 12 и В = 4 × 3 = 12. Теперь сумма Г + В = 24 отлична от суммы Р + 2 = 26. Наше предположение, взятое в полной общности, оказалось неверным!

Мы можем, конечно, сказать, что не намеревались установить предположение в такой общности, что мы все время имели в виду многогранники выпуклые, или, так сказать, «сферообразные» а не «баранкообразные», как рама для картины. Но это отговорки. Фактически мы должны изменить свою позицию, а с нею и свое первоначальное утверждение. Вполне возможно, что удар, который мы получили, в конце концов окажется благотворным и приведет в конечном счете к исправленной и более точной формулировке нашего предположения. Но как бы то ни было, это был удар по нашей уверенности.

7. Аналогия. Пример «рамы для картины» убил наше предположение в его первоначальной форме, но оно может быть немедленно возрождено в исправленной (и, будем надеяться, улучшенной) форме, с важным ограничением.

64

Тетраэдр является выпуклым телом, и таким же является куб, и такими же являются другие многогранники в нашей коллекции (рис. 3.1), и такими же являются все многогранники, которые мы можем из них получить с помощью усечения и «умеренной» пристройки крыш (пристройки достаточно ровных крыш к их различным граням). Во всяком случае, не существует опасности, что эти операции могли бы от выпуклого, или «сферообразного» многогранника привести к «баранкообразному» телу.

Замечая это, мы вводим уточнение, которое здесь очень нужно. Мы высказываем предположение, что для любого выпуклого многогранника между числами граней, вершин и ребер имеет место соотношение Г + В = Р + 2. (Можно было бы даже предпочесть ограничиться «сферообразными» многогранниками, но мы не хотим здесь останавливаться на определении значения этого термина.)

Это предположение имеет некоторые шансы быть верным. Тем не менее наша уверенность была поколеблена и мы хотели бы найти какое-нибудь новое подкрепление для своего предложения. Мы не можем надеяться на большую помощь от дальнейших подтверждений. Кажется, что мы исчерпали наиболее очевидные источники. Однако мы можем еще надеяться на некоторую помощь от аналогии. Существует ли какой-нибудь более простой аналогичный случай, который мог бы оказаться поучительным?

Многоугольники аналогичны многогранникам. Многоугольник есть часть плоскости, как многогранник — часть пространства. Многоугольник имеет некоторое число В вершин (вершин его углов) и некоторое число Р ребер (или сторон). Очевидно,

В = Р.

Однако это соотношение, справедливое для выпуклых многоугольников, кажется слишком простым и проливает мало света на более сложное соотношение

Г + В = Р + 2,

которое, как мы подозреваем, справедливо для выпуклых многоугольников.

Если мы по-настоящему заинтересованы рассматриваемым вопросом, то мы, естественно, пытаемся подвести эти соотношения поближе друг к другу. Существует остроумный способ, позволяющий сделать это. Сначала нужно расположить рассматриваемые числа в естественном порядке. Многогранник трехмерен, его грани (многоугольники) двумерны, его ребра одномерны и его вершины (точки), конечно, нульмерны. Мы можем теперь переписать наши равенства, располагая величины в порядке возрастания размерности. Соотношение для многоугольников, написанное в виде

В — Р + 1 = 1,

65

становится сравнимым с соотношением для многогранников, записанным в виде

В — Р + Г — 1 = 1.

Единица в левой части равенства для многоугольников соответствует единственному имеющемуся двумерному элементу — внутренности многоугольника. Единица в левой части равенства для многогранников соответствует единственному имеющемуся трехмерному элементу — внутренности многогранника. Числа в левой части равенства, подсчитывающие соответственно элементы нульмерные, одномерные, двумерные и трехмерные, расположены в своем естественном порядке и имеют чередующиеся знаки. Правая часть равенства в обоих случаях одинакова; аналогия кажется полной. Поскольку первое равенство для многоугольников, очевидно, верно, то аналогия увеличивает нашу уверенность во втором равенстве для многогранников, предположение о котором мы сделали.

8. Разбиение пространства. Мы переходим теперь к другому примеру индуктивного исследования в пространственной геометрии. В своем предыдущем примере мы отправлялись от общего, до некоторой степени туманного, замечания. Нашей отправной точкой теперь будет конкретная, имеющая ясные очертания задача. Рассмотрим простую, но не слишком знакомую задачу пространственной геометрии: На сколько частей пространство делится пятью плоскостями?

На этот вопрос легко ответить, если пять данных плоскостей параллельны между собой; в этом случае пространство, очевидно, делится на 6 частей. Этот случай, однако, является слишком специальным. Если наши плоскости находятся в «общем положении», то никакие две из них не будут параллельны и будет иметься значительно больше частей, чем 6. нашу задачу нужно сформулировать более точно, добавив существенный пункт: _На сколько частей пространство делится пятью плоскостями при условии, что эти плоскости находятся в общем положении?

Идея «общего положения» интуитивно совершенно понятна; плоскости находятся в таком положении, когда они не связаны специальными соотношениями, когда они заданы независимо, выбраны наугад. Было бы нетрудно сделать этот термин совершенно точным с помощью формального определения, но мы этого не будем делать по двум причинам. Во-первых, изложение не должно быть слишком формальным. Во-вторых, оставляя понятие несколько неясным, мы ближе подходим к позиции натуралиста, которыйф часто вынужден начинать с не совсем ясных понятий, но уточняет их по мере продвижения.

66

9. Видоизменение задачи. Сосредоточим внимание на нашей задаче. Нам даны 5 плоскостей в общем положении. Они разрезают пространство на определенное число частей. (Мы можем представить себе сыр, рассеченный на куски пятью прямолинейными разрезами острого ножа.) Нам нужно найти число этих частей. (На сколько частей разрезается сыр?)

Кажется трудным сразу увидеть все части, на которые пространство разбивается пятью плоскостями. (Может быть, невозможно их «увидеть». Как бы то ни было, не перенапрягайте своего воображения[12], лучше попытайтесь думать. Ваш разум может повести вас дальше, чем ваше воображение[13].) Но почему именно пять плоскостей? Почему не любое число плоскостей? На сколько частей пространство делится четырьмя плоскостями? Тремя плоскостями? Или двумя плоскостями? Или всего лишь одной плоскостью. Мы подошли здесь к случаям,доступным нашей геометрической интуиции. Одна плоскость, очевидно, делит пространство на 2 части. Две плоскости, если они параллельны, делят пространство на 3 части. Мы должны, однако, отбросить это специальное расположение; 2 плоскости, находящиеся в общем положении, пересекаются и делят пространство на 4 части. Три плоскости, находящиеся в общем положении, делят пространство на 8 частей. Чтобы ясно понять этот последний, более трудный, случай, можно представить себе две вертикальные стены внутри здания, пересекающие одна другую, и горизонтальное перекрытие, поддерживаемое палками, пересекающее обе стены и образующее вокруг точки, где оно пересекается со стенами, одновременно пол четырех комнат и потолок других четырех комнат.

10. Обобщение, специализация, аналогия. Наша задача относится к 5 плоскостям, но вместо того, чтобы рассматривать 5 плоскостей, сначала мы занялись 1, 2 и 3 плоскостями. Не потратили ли мы свое время зря? Совсем нет. Исследуя более простые аналогичные случаи, мы готовились к нашей задаче. Мы пробовали свои силы на этих более простых случаях; мы выяснили необходимые понятия и познакомились с тем типом задач, с которым должны встретиться.

Даже путь, который привел нас к этим более простым аналогичным задачам, типичен и заслуживает внимания. Сначала мы перешли от случай 5 плоскостей к случаю любого числа плоскостей, скажем, n плоскостей: мы произвели обобщение. Затем от n плоскостей мы вернулись к 4 плоскостям, к 3 плоскостям, к 2 плоскостям, к всего лишь одной плоскости, т. е. в общей задаче мы положили n = 4, 3, 2, 1: мы произвели специализацию. Но задача о делении пространства, скажем, тремя плоскостями аналогична нашему первоначальному вопросу относительно пяти плоскостей. Итак, мы пришли к аналогии обычным путем, вступительным обобщением и последующей специализацией.

67

11. Одна аналогичная задача. Как обстоит дело со следующим случаем четырех плоскостей?

Четыре плоскости, находящиеся в общем положении. Определяют различные части пространства, одна из которых ограничена, заключена между четырьмя треугольными гранями и называется тетраэдром (см. рис 3.3). Эта конфигурация напоминает нам три прямые линии на плоскости, находящиеся в общем положении и определяющие различные части плоскости, одна из которых ограничена, заключена между тремя прямолинейными отрезками и является треугольником (см. рис. 3.4). Нам нужно установить число частей пространства, определяемых четырьмя плоскостями. Попробуем свои силы на более простой аналогичной задаче: На сколько частей плоскость делится тремя прямыми? Многие из нас увидят ответ немедленно, даже не вычерчивая фигуры, и каждый может его увидеть, пользуясь грубым наброском (см. рис 3.4). Искомое число частей равно 7.

Рис. 3.3 Пространство, разделенное четырьмя плоскостями.	Рис. 3.4. Плоскость, разделенная тремя прямыми.

Мы нашли решение более простой аналогичной задачи; но можем ли мы воспользоваться этим решением для своей первоначальной задачи? Да, можем, если будем разумно обращаться с аналогией двух конфигураций. Нам следует так подойти к разбиению плоскости тремя прямыми, чтобы после этого мы смогли тот же самый подход применить к разбиению пространства четырьмя плоскостями.

Итак, посмотрим снова на разбиение плоскости тремя прямыми, ограничивающими треугольник. Одна часть конечна — это внутренность треугольника. А бесконечные части имеют с треугольником или общую сторону (имеются три такие части) или общую вершину (имеются также три части этого типа) Таким образом, число всех частей равно 1 + 3 + 3 = 7.

68

Теперь рассмотрим разбиение пространства четырьмя плоскостями, ограничивающими тетраэдр. Одна часть конечна, это внутренность тетраэдра. Бесконечная часть может иметь общую грань (двумерный элемент границы) с тетраэдром (имеются 4 такие части) или общее ребро (одномерный элемент границы; имеются 6 частей этого типа) или общую вершину (нульмерный элемент границы; имеются 4 части этого типа, показанные на рис. 3.3). Таким образом, число всех частей равно 1 + 4+ 6 + 4 = 15.

Мы пришли к этому результату с помощью аналогии и воспользовались аналогией типичным, важным способом. Сначала мы придумали более легкую аналогичную задачу и решили ее. Затем, чтобы решить первоначальную более трудную задачу (о тетраэдре), мы воспользовались новой более легкой аналогичной задачей (о треугольнике) как моделью; при решении более трудной задачи мы следовали образцу решения более легкой задачи. Но прежде чем сделать это, мы должны были пересмотреть решение более легкой задачи. Мы перестроили его, переделали в новый образец, пригодный для подражания.

Выделить аналогичную более легкую задачу, решить ее, переделать ее решение так, чтобы оно могло служить в качестве модели, и наконец добиться решения первоначальной задачи, следуя только что созданной модели, — этот метод непосвященному может казаться окольным. Но он часто применяется в математических и нематематических научных исследованиях.

12. Серия аналогичных задач. Однако наша первоначальная задача все еще не решена. Она относится к разбиению пространства пятью плоскостями. Какова аналогичная задача для двух измерений? Разбиение пятью прямыми? Или четырьмя прямыми? Для нас лучше, быть может, рассмотреть эти задачи в полной общности: разбиение пространства n плоскостями и разбиение плоскости n прямыми. Эти разбивающие прямые должны, конечно, находиться в общем положении (никакие 2 не параллельны и никакие 3 не имеют общей точки).

Если мы привыкли пользоваться геометрической аналогией, то можем сделать еще один шаг и рассмотреть деление прямой линии n общими точками. Хотя эта задача совсем тривиальна, она может оказаться поучительной. Мы легко видим, что прямая делится одной точкой на две части, двумя точками на 3, тремя точками на 4 и вообще n точками на n + 1 частей.

Опять-таки, если мы привыкли обращать внимание на крайние случаи, то можем рассмотреть неразделенное пространство, плоскость или прямую и считать его «разбиением, осуществленным 0 разбивающих элементов».

Составим следующую таблицу, исчерпывающую все наши результаты полученные до сих пор

Число делящих элементов	Число частей при делении
	пространства плоскостями	плоскости прямыми	прямой точками
0 1 2 3 4 … n	1 2 4 8 15 …	1 2 4 7 …	1 2 3 4 5 … n+1

13. Много задач иногда легче решить, чем только одну. Мы собирались решить задачу, относящуюся к разбиению пространства пять плоскостями. Мы ее еще не решили, но поставили много новых задач. Каждое незаполненное в нашей таблице место соответствует открытому вопросу.

Этот прием накопления новых задач непосвященному может показаться глупым. Но некоторый опыт в решении задач может научить нас, что много задач вместе иногда решить легче, чем всего лишь одну из них, если это большое число задач хорошо согласовано, а одна задача сама по себе изолирована[14]. Наша первоначальная задача выступает теперь в качестве одной из задач в серии нерешенных задач. Но дело в том, что все эти нерешенные задачи образуют серию: они хорошо расположены, сгруппированы вместе, находятся в тесной аналогии между собой и с несколькими уже решенными задачами. Если мы сравним теперешнее положение нашего вопроса, хорошо включенного в серию аналогичных вопросов, с его исходным положением, когда он был еще полностью изолирован, то мы, естественно, будем склонны поверить, что было сделано некоторое продвижение.

14. Предположение. Посмотрим на результаты, представленные в нашей таблице, как натуралист смотрит на коллекцию своих образцов. Эта таблица бросает вызов нашей изобретательности. Нашей способности наблюдать. Сумеем ли мы обнаружить какую-нибудь связь, какую-нибудь закономерность?

Рассматривая второй столбец (деление пространства плоскостями), мы можем заметить, что в последовательности 1, 2, 4, 8, … имеется ясная закономерность; мы видим здесь последовательные степени числа 2. Но что за разочарование! Следующий член в этом столбце 15, а не 16, как мы ожидали. Наша догадка была не так уж хороша; нужно поискать что-нибудь другое.

В конечном счете мы можем случайно наткнуться на сложение двух рядом расположенных чисел и заметить, что в таблице имеется их сумма. Мы подмечаем своеобразную связь: число из таблицы мы

70

получаем, складывая два других числа: число, расположенное над ним и число, находящееся справа от последнего. Например, числа

8	7
15

связаны соотношением

8 + 7 = 15

Это замечательная связь, поразительный ключ. Кажется невероятным, чтобы эта связь, которую мы можем наблюдать во всей таблице, так далеко вычисленной, могла быть результатом простой случайности.

Итак, эта ситуация наводит на мысль, что замеченная закономерность распространяется и за пределы наших наблюдений, что еще не найденные числа таблицы связаны в точности так же, как и уже вычисленные. И, таким образом, мы приходим к предположению, что закон, на который мы наткнулись случайно, справедлив всегда.

Если это так, то мы можем решить свою первоначальную задачу. Складывая расположенные рядом числа, мы можем продолжить нашу таблицу до тех пор, пока не достигнем числа которое хотим получить:

0	1	1	1
1	2	2	2
2	4	4	3
3	8	7	4
4	15	11	5
5	26

В таблице, как она здесь перепечатана, появились два новых числа, набранных жирным шрифтом и вычисленных путем сложения, 11 = 7 + 4, 26 = 15 + 11. Если наша догадка правильна, то число частей, на которые пространство разбивается пятью плоскостями, находящимися в общем положении, должно равняться 26. кажется, мы решили предложенную задачу, или по крайней мере нам удалось уловить правдоподобное предположение, подкрепляемое всеми до сих пор собранными наблюдениями.

15. Предсказание и подтверждение. В предыдущем мы в точности следовали типичному образу действий натуралиста. Если натуралист наблюдает поразительную закономерность, которая не может быть разумно приписана простой случайности, то он делает предположение, что эта закономерность продолжается и за пределами его фактических наблюдений. Принятие такого предположения часто является решающим шагом в индуктивном исследовании[15].

Следующим шагом может быть предсказание. На основании своих ранее сделанных наблюдений и их согласия с предполагаемым зако-

71

ном натуралист предсказывает результат своего следующего наблюдения. Многое зависит от исхода этого следующего наблюдения. Окажется ли предсказание верным или нет? Мы находимся точно в таком же положении. Мы нашли, или, точнее, догадались или предсказали, что число областей, на которые плоскость разбивается четырьмя прямыми, находящимися в общем положении, равно 11. Так ли это? Правильно ли наше предположение?

Рис. 3.5. Плоскость, разделенная четырьмя прямыми.

Исследуя грубый набросок (см. рис 3.5), мы убедимся, что наша догадка была хорошей, что число 11 действительно есть правильное число. Это подтверждение нашего предсказания дает индуктивные доводы в пользу правила, на основании которого мы сделали свое предсказание. Успешно выдержав испытание, наше предположение вышло из него окрепшим.

16. Снова и лучше. Мы убедились, что число 11 верно, рассматривая фигуру и подсчитывая число частей. Да, 4 прямые, находящиеся в общем положении, по-видимому, делят плоскость на 11 частей. Но проделаем это снова и проделаем лучше. Мы подсчитали эти части каким-то образом. Подсчитаем их снова и подсчитаем так, чтобы быть уверенными в том, что избежали путаницы и ошибок, и ловушек, расставленных специальными положениями прямых.

Начнем с того факта, что 3 прямые определяют точно 7 частей плоскости. Мы имеем некоторые основания верить, что 4 прямые определяют 11 частей. Почему ровно на 4 части больше? Почему в этой связи появляется число 4? Почему проведение новой прямой увеличивает число частей ровно на четыре?

Рис. 3.6. Переход от трех прямых к четырем.

Выделим на рис 3.5 одну прямую и перечертим ее пунктиром (см. рис. 3.6). Новая фигура не слишком отличается от старой по виду, но она выражает совсем другой подход. Мы рассматриваем выделенную прямую как новую, а три другие прямые как старые. Старые прямые рассекают плоскость на 7 частей. Что происходит, когда добавляется новая прямая?

Новая прямая, начерченная наугад, должна пересекать каждую старую прямую и притом в разных точках. Это дает 3 точки. Эти

72

3 точки делят новую прямую на 4 отрезка. Каждый отрезок разрезает старую часть плоскости, делает две новых части[16] из одной старой. Вместе 4 отрезка новой прямой создают 8 новый частей и упраздняют 4 старые части — число частей возрастает ровно на 4. вот причина того, что число частей теперь ровно на четыре больше, чем оно было раньше:

7 + 4 = 11.

Этот путь получения числа 11 убедителен и ярко освещает рассматриваемую задачу. Мы можем усмотреть теперь основание для закономерности, которую мы наблюдали и на которой основывали свое предсказание этого числа 11. мы начинаем подозревать, какое объяснение скрывается за фактами, и наша вера в то, что наблюдаемая закономерность всегда справедлива, чрезвычайно усилилась.

17. Индукция подсказывает дедукцию; частный случай подсказывает общее доказательство. Мы все время тщательно указывали на параллелизм между нашими рассуждениями и образом действий натуралиста[17]. Мы начали с частной задачи, как натуралист может начать со ставящего в тупик наблюдения[18]. Мы продвигались вперед с помощью пробных обобщений, отмечая доступные частные случаи, наблюдая поучительные аналогии. Мы попытались угадать некоторую закономерность и ошиблись, попытались снова и сделали это лучше. Нам удалось предложить общий закон, который подкреплялся всеми экспериментальными данными, бывшими в нашем распоряжении. Мы подвергли испытанию еще один частный случай и нашли согласие с предполагаемым законом, авторитет которого выиграл от такого подтверждения. Наконец, мы заметили основание для этого общего закона, своего рода объяснение и наша вера значительно усилилась. Исследование натуралиста может проходить в точности через те же самые фазы.

Существует, однако, место, где дороги математика и натуралиста резко расходятся. Наблюдение является высшим авторитетом для натуралиста[19], но не для математика. Подтверждение во многих хорошо выбранных примерах есть единственный способ подкрепления предполагаемого закона в естественных науках. Подтверждение во многих хорошо выбранных примерах может быть очень полезно в качестве поощрения. Но никогда не может доказать предполагаемый закон в математических науках[20]. Рассмотрим наш собственный конкретный случай. Исследование различных частных случаев и сравнение их привело нас к предположению об общем правиле, из которого следует, что решением нашей первоначально предложенной задачи является число 26. достаточны ли все наши наблюдения и подтверждения для доказательства этого общего правила? Или могут ли они доказать частный результат, что решением нашей задачи действительно является 26? Ни в малейшей степени. Для математика с жесткими

73

стандартами число 26 есть только определенная догадка, и подозреваемое общее правило не может быть доказано никаким количеством экспериментальных подтверждений. Индукция делает свои результаты вероятными, она никогда их не доказывает[21].

Можно, однако, заметить, что индуктивное исследование может быть в математике полезно в другом отношении, о котором мы еще не упоминали. Тщательное наблюдение частных случаев, которые приводят нас к общему математическому результату, может также подсказать его доказательство. Из внимательного исследования частного случая может возникнуть общее понимание.

В самом деле, это действительно произошло с нами уже в предыдущем параграфе. Общее правило, которое мы открыли с помощью индукции, относится к двум расположенным рядом числам в нашей таблице, как, напри мер, 7 и 4, и к их сумме, которая в этом случае равна 11. Далее, в предыдущем параграф мы яно увидели геометрическое значение чисел 7, 4 и 11 в нашей задаче и при этом поняли, почему там возникает соотношение 7 + 4 = 11. Мы фактически имели дело с переходом от 3 прямых, делящих плоскость, к 4 таким прямым. Однако в числах 3 и 4 нет никаких особых достоинств; точно так же мы могли бы перейти от любого целого числа к следующему, от n к n + 1. Рассмотренный частный случай может представлять нам всю ситуацию (пример 2.10). Я предоставляю читателю удовольствие полностью извлечь общую идею из частного наблюдения предыдущего параграфа. При этом он может дать формальное доказательство для индуктивно открытого правила, по крайней мере насколько это относится к двум последним столбцам.

Все же, чтобы завершить доказательство, мы должны не только рассмотреть разбиение плоскости прямыми, но и разбиение пространства плоскостями. Мы можем, однако, надеяться, что если мы в состоянии разобраться с разбиениями плоскости, то аналогия поможет нам разобраться и с разбиениями пространства. Снова я предоставляю читателю удовольствие извлечь пользу из совета, который дает аналогия.

18. Еще предположения. Мы не исчерпали еще тему о разбиениях плоскости и пространства. Осталось еще сделать несколько маленьких открытий, и они вполне доступны индуктивным рассуждениям. Нас легко может привести к ним тщательное наблюдение и сделанное с пониманием сопоставление частных примеров.

Мы можем пожелать найти формулу для числа частей, образуемых при разбиении плоскости n прямыми, находящимися в общем положении. Фактически у нас уже есть формула в простейшем аналогичном случае: n различных точек делят прямую на n + 1 отрезков. Эта аналогичная формула, частные случаи, записанные в нашей таблице, наше индуктивно открытое общее правило (которое мы почти доказали), все наши результаты, полученные до сих пор, могут помочь

74

нам решить эту задачу. Я не вхожу в детали. Я просто отмечу решение, которое можно найти, следуя только что сделанным намекам, разными способами.

Число частей, на которые прямая делится n различными точками, равно n + 1. Число частей, на которые плоскость делится n прямыми, находящимися в общем положении, равно

Читатель может вывести последнюю формулу или по крайней мере проверить ее в простейших случаях, для n = 0, 1, 2, 3, 4. Я также предоставляю читателю удовольствие открыть третью формулу того же типа для числа частей пространства. Делая это маленькое открытие, читатель может расширить свой опыт индуктивных рассуждений в математических вопросах и почувствовать ту приятную помощь, которую оказывает нам аналогия при решении задач, больших или малых.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ III

Формула Г + В = Р + 2, предположение о которой мы высказали в § 1, принадлежит Леонарду Эйлеру. Мы называем ее «формулой Эйлера», рассматриваем как предположение и исследуем различными способами в примерах 1—10, иногда индуктивно, а иногда с целью найти доказательство. Мы возвращаемся к ней в примерах 21—30 и 31—41. Перед тем как приняться за какой-нибудь пример в этих разделах, прочтите соответственно примеры 21 и 31.

1. Две пирамиды, расположенные по разные стороны от их общего основания, вместе образуют «двойную пирамиду». Октаэдр есть частный случай двойной пирамиды; общее основание — квадрат. Имеет ли место формула Эйлера для произвольной двойной пирамиды?

2. Возьмите выпуклый многогранник с Г гранями, В вершинами и Р ребрами, выберите внутри него точку О (например, его центр тяжести), опишите шар с центром О и спроектируйте многогранник из центра О на поверхность шара. Эта проекция переводит Г граней в Г областей, или «стран» на поверхности шара, любое из ребер она переводит в граничную линию, разделяющую две соседние страны, и любую из В вершин — в «угол» или общую границу трех или более стран («угол трех стран» или «угол четырех стран» и т. д.). эта проекция дает граничные линии особенно простой природы (дуги больших кругов), но, очевидно, справедливость формулы Эйлера для такого подразделения поверхности шара на страны не зависит от точной формы граничных линий; на числа Г, В и Р не оказывает влияния непрерывная деформация этих линий.

(1) Меридиан есть половина окружности большого круга, соединяющая два полюса, южный и северный. Параллель есть пересечение поверхности шара с плоскостью, параллельной экватору. Поверхность шара делится m меридианами и p параллелями на Г стран. Вычислите Г, В и Р. Имеет ли место формула Эйлера?

(2) Проекция октаэдра из его центра на поверхность шара является частным случаем ситуации, описанной в (1). Для каких значений m и p?

3. Случай играет некоторую роль в открытии. Индуктивное открытие, очевидно, зависит от наблюдаемого материала. В § 1 мы встретились с несколькими многогранниками, но случайно могли бы натолкнуться и на другие. Вероятно, мы не пропустили бы правильные многогранники, но наш перечень мог бы появиться в таком виде:

75

Многогранники	Г	В	Р
Тетраэдр	4	4	6
Куб	6	8	12
Октаэдр	8	6	12
Пятигранная призма	7	10	15
Пятигранная двойная призма	10	7	15
Додекаэдр	12	20	30
Икосаэдр	20	12	30

Наблюдаете ли вы какую-нибудь закономерность? Можете ли вы ее объяснить? Какова связь с формулой Эйлера?

4. Попытайтесь обобщить соотношение между двумя многогранниками, наблюдаемое в таблице примера 3. [Соотношение, описанное в решении примера 3 в (2), слишком «узко» и «детально». Возьмите, однако, куб и октаэдр в описанной там ситуации, окрасьте ребра одного красной, а другого — синей краской и спроектируйте их из их общего центра Р на поверхность шара, как описано в примере 2. затем сделайте обобщение.]

5. Было бы достаточно доказать формулу Эйлера в частном случае: для выпуклых многогранников, имеющих только трехгранные вершины. Почему? [§ 4.]

6. Было достаточно доказать формулу Эйлера в частном случае: для выпуклых многогранников, имеющих только трехгранные вершины. Почему? [§ 4.]

7. При доказательстве формулы Эйлера мы можем ограничиться плоскими фигурами. Действительно, представьте себе, что Г — 1 граней многогранника сделаны из картона, а одна грань из стекла; назовем эту грань «окном». Вы смотрите через окно внутрь многогранника, причем ваши глаза находятся так близко к окну, что вам видна вся внутренность многогранника. (Это может оказаться неосуществимым, если многогранник не является выпуклым.) То, что вы видите, вы можете интерпретировать как плоскую фигуру, начерченную на оконном стекле: вы видите подразделение окна на более мелкие многоугольники. В этом подразделении имеется N₂ многоугольников, N₁ прямых граничных лини (некоторые внешние, некоторые внутренние) и N₀ вершин.

(1) Выразите N₀, N₁ и N₂ через Г, В и Р.

(2) Если для Г, В и Р имеет место формула Эйлера, то какая формула имеет место для N₀, N₁ и N₂?

8. Прямоугольник имеет l см в длину и m см в ширину; l и m — целые числа. Прямоугольник подразделяется на lm равных квадратов прямыми, параллельными его сторонам.

(1) Выразите N₀, N₁ и N₂ через Г, В и Р.

(2) Справедливо ли соотношение примера 7 (2) в этом случае?

9. Примеры 5 и 7 наводят на мысль, что нам нужно было бы исследовать подразделение треугольника на N₂ треугольников с N₀ — 3 вершинами внутри подразделяемого треугольника. Вычисляя суммы всех углов в этих N₂ треугольниках двумя различными способами, вы можете доказать формулу Эйлера.

10. § 7 наводит на мысль распространить формулу Эйлера на случай четырех и большего числа измерений. Как мы могли бы сделать такое распространение осязаемым? Как можно было бы ясно его себе представить?

Пример 7 показывает, что случай многогранника может быть сведен к подразделению плоского многоугольника. Аналогия подсказывает, что случай четырех измерений можно свести к подразделению многогранника в нашем видимом трехмерном пространстве. Если мы хотим действовать индуктивно, то должны исследовать какие-нибудь примеры такого подразделения. По аналогии с примером 8 возникает следующий пример.

Ящик (т. е. прямоугольный параллелепипед) имеет измерения l, m и n; эти три числа целые. Ящик подразделяется lmn равных кубов плоскостями, параллельными его граням. пусть N₀, N₁ и N₂ обозначают соответственно число вершин, ребер, граней и многогранников (кубов), образующих подразделение.

76

(1) Выразите N₀, N₁ и N₂ через l, m и n.

(2) Существует ли соотношение, аналогичное равенству (2) в решении примера 7?

11. Пусть L_n обозначает число частей, на которые плоскость делится n прямыми линиями, находящимися в общем положении. Докажите, что L_n+1 = L_n + (n +1).

12. Пусть S_n обозначает число частей, на которые пространство делится n плоскостями в общем положении. Докажите, что S_n+1 = S_n + L_n.

13. Проверьте предполагаемую формулу

для n = 0, 1, 2, 3, 4.

14. Догадайтесь, какова должна быть формула дляS_n, и убедитесь, что она верна для n = 0, 1, 2, 3, 4.

15. Сколько частей из тех 11, на которые плоскость делится четырьмя прямыми, находящимися в общем положении, являются конечными? [Сколько бесконечными?]

16. Обобщите предыдущую задачу?

17. Сколько частей из тех 26, на которые пространство делится пятью плоскостями, являются бесконечными?

18. Пять плоскостей проходят через центр шара, но в других отношениях их положение является общим. Найдите число частей, на которые поверхность шара делится этими пятью плоскостями.

19. На сколько частей делится плоскость пятью попарно пересекающимися окружностями, находящимися в общем положении?[22]

20. Обобщите предыдущие задачи.

21. _Индукция: приспособление ума, приспособление языка. Индукция имеет результатом приспособление нашего ума к фактам. Когда мы сравниваем наши идеи с наблюдениями, то может иметь место согласие или несогласие. Если имеет место согласие, то мы чувствуем бо́льшую уверенность в своих идеях; если имеет место несогласие, то мы видоизменяем свои идеи. После повторных видоизменений наши идеи могут несколько лучше соответствовать фактам. Первые наши идеи о новом предмете почти обязаны быть ошибочными, по крайней мере частично; индуктивный процесс дает нам возможность исправить их, приспособить их к действительности. Наши примеры показывают этот процесс в малом масштабе, но довольно ясно. В § 1 после двух или трех ошибочных предположений мы в конечном счете пришли к правильному предположению. Вы можете сказать, что мы пришли к нему случайно. «Однако такие случаи встречаются только людям, которые их заслуживают», — как однажды сказал Лагранж, когда обсуждалось одно несравненно более великое открытие Ньютона.

Приспособление ума может в большей или меньшей степени совпадать с приспособлением языка; как бы то ни было, одно идет рука об руку с другим. Прогресс науки отмечается прогрессом терминологии. Когда физики начинали говорить об «электричестве» или врачи об «инфекции», эти термины были туманными, неясными, путаными. Термины, которыми ученые пользуются сегодня, как, например, «электрический заряд», «электрический ток», «грибковая инфекция», «вирусная инфекция», являются несравненно более ясными и более определенными. Но между этими двумя терминологиями лежит огромное количество наблюдений, искусных экспериментов, а также несколько великих открытий. Индукция изменила терминологию, выяснила понятия. Мы можем проиллюстрировать и эту сторону процесса, т. е. индуктивное выяснение понятий, подходящим небольшим математическим примером. Вот ситуация, не столь уж нечастая в математическом исследовании: теорема уже сформулирована, но мы должны придать более точный смысл терминам, в которых она сформулирована, чтобы сделать ее безукоризненно правильной. Это, как мы увидим, может быть удобно сделано с помощью индуктивного процесса[23].

77

Обратимся снова к примеру 2 и его решению. Мы говорили о «подразделении поверхности шара на страны», не предлагая формального определения этого термина. Мы надеялись, что формула Эйлера останется справедливой, если Г, Р и В обозначают число стран, граничных линий и углов в таком подразделении. Однако мы снова полагались на примеры и грубое описание и не дали формального определения для Г, Р и В. в таком точном смысле следовало бы нам взять эти термины, чтобы сделать формулу Эйлера безукоризненно правильной? Вот наш вопрос.

Мы будем называть подразделение сферы (т. е. поверхности шара) с соответствующим истолкованием символов Г, Р и В «нормальным, если имеет место формула Эйлера, и «ненормальным», если эта формула не имеет места. Приведите примеры подразделений, которые могли бы помочь нам обнаружить какое-нибудь ясное и простое различие между «нормальными» и «ненормальными» случаями.

22. Полная поверхность шара состоит только из одной страны. Нормально ли это? (Мы подразумеваем: «нормально» с точки зрения формулы Эйлера.)

23. Поверхность шара делится точно на две страны, западное полушарие и восточное полушарие, разделенные большим кругом. Ненормально ли это?

24. Две параллели делят сферу на три страны. Нормально это или ненормально?

25. Три меридиана делят сферу на три страны. Нормально это или ненормально?

26. Назовите подразделение сферы m меридианами и p параллелями «подразделением (m, p) (ср. пример 26) могут быть порождены процессом, описанным в примере 2? (Проектирование выпуклого многогранника на сферу, за которой следует непрерывная деформация границ, оставляющая неизменным число стран и число граничных линий вокруг каждой страны.) какие условия относительно m и p характеризуют такие подразделения?

29. Что ненормально в примерах, в которых не имеет места формула Эйлера? Какие геометрические условия, делающие более точным смысл Г, В и Р, обеспечили бы выполнение формулы Эйлера?

30. Приведите еще примеры, иллюстрирующие ответ на пример 29.

31. Работа Декарта о многогранниках. Среди рукописей, оставленных Декартом, имелись короткие заметки об общей теории многогранников. Копия этих заметок (сделанная рукой Лейбница) была обнаружена и опубликована в 1860 г., более через двести лет после смерти Декарта; см. Œuvres vol. 10. p. 257—276. Эти заметки посвящены вопросу, тесно связанному с теоремой Эйлера: хотя заметки не устанавливают этой теоремы в явной форме, они содержат результаты, из которых она немедленно следует.

Рассмотрим вместе с Декартом выпуклый Многогранник. Назовем любой угол любой грани этого многогранника _поверхностным углом и пусть ∑α обозначает сумму всех поверхностных углов. Декарт вычисляет ∑α двумя различными способами, и теорема Эйлера немедленно получается из сравнения двух выражений.

Нижеследующие примеры дают читателю возможность восстановить некоторые из выводов Декарта. Мы будем пользоваться следующими обозначениями:

Г_n обозначает число граней с n ребрами,

В_n — число вершин, в которых оканчиваются n ребер, так что

Г₃ + Г₄ + Г₅ + … = Г,

В₃ + В₄ + В₅ + … = В.

Мы продолжаем обозначать символом Р число всех ребер многогранника.

78

32. Выразите число всех поверхностных углов тремя различными способами: соответственно через Г₃, Г₄, Г₅, … В₃, В₄, В₅, … и через Р.

33. Вычислите ∑α для пяти правильных многогранников: тетраэдра, куба, октаэдра, додэкаэдра[24] и икосаэдра.

34. Выразите ∑α через Г₃, Г₄, Г₅, …

35. Выразите ∑α через Р и Г.

36. Дополнительные телесные углы, дополнительные сферические многоугольники. Мы называем телесным углом то, что чаще называется многогранным углом.

Пусть два выпуклых телесных угла имеют одинаковое число граней и общую вершину, но не имеют никаких других общих точек. Каждой грани одного телесного угла соответствует ребро другого, и эта грань перпендикулярна соответствующему ребру. (Это отношение между двумя телесными углами взаимно: ребро e, линия пересечения двух соседних граней первого телесного угла, соответствует грани f̍' второго телесного угла, если f̍' ограничена двумя ребрами, соответствующими двум вышеупомянутым граням.) Два телесных угла, находящихся в этом взаимном отношении, называются дополнительными телесными углами. (Это название не является обычным, но два обыкновенных дополнительных угла можно перевести в аналогичное взаимное положение.) Каждый из двух дополнительных телесных углов называется дополнением другого.

Сфера радиуса 1, описанная из общей вершины двух дополнительных телесных углов, как из центра, пересекается ими по двум сферическим многоугольникам, и эти многоугольники называются дополнительными. Рассмотрим два дополнительных сферических многоугольника. Пусть a₁, a₂, …, a_n — его углы, A — его площадь, P — его периметр и пусть a'₁, a'₂, …, a'_n, a'₁, a'₂, …, a'_n, A', P' обозначают соответствующие части другого многоугольника. Тогда, если обозначения выбраны подходящим образом

a₁, + a'₁ = a₂ + a'₂ = … = a_n + a'_n = π,

a'₁, + a₁ = a'₂ + a₂ = … = a'_n + a_n = π,

это хорошо известно и легко проверить

Докажите, что

Р + A' = P'+ A = 2π

[примите как известное, что площадь сферического треугольника с углами α, δ и γ равна «сферическому избытку α, + δ + γ — π (радиус сферы равен 1)]

37. «Как в плоской фигуре все внешние углы вместе равны 4 прямым углам так в пространственном теле все внешние телесные углы вместе равны 8 прямым углам». Попытайтесь интерпретировать это замечание, найденное в заметках Декарта, как теорему, которую вы можете доказать. (См. рис. 3.7.)

Рис. 3.7. Внешние углы многоугольника.

38. Выразите ∑α через В.

39. Докажите теорему Эйлера.

40. Начальное замечание § 1 туманно, но может навести на мысль о некоторых точных утверждениях. Вот одно, не рассмотренное нами в § 1: «Если любая из трех величин Г, В и Р стремится к ∞, то и две другие величины должны стремиться к ∞». Докажите следующие неравенства, имеющие место

79

для произвольных выпуклых многогранников и дайте еще более точную информацию:

2Р ≥ 3Г, 2В ≥ Г + 4, 3В ≥ Р + 6,

2Р ≥ 3В, 2Г ≥ В + 4, 3Г ≥ Р + 6,

Может ли в этих неравенствах достигаться равенство? Для какого вида многогранников может оно достигаться?

41. Существуют выпуклые многогранники, все грани которых являются многоугольниками одного и того же типа, т. Е. Многоугольниками с одинаковым числом сторон. Например, все грани тетраэдра являются треугольниками, все грани параллелепипеда – четырехугольниками, все грани правильного додекаэдра — пятиугольниками. «И так далее», быть может, хочется вам сказать. Однако такая простая индукция может ввести в заблуждение: не существует выпуклых многогранников, все грани которых были бы шестиугольниками. Попытайтесь это доказать. [Пример 31.]

IV. ИНДУКЦИЯ В ТЕОРИИ ЧИСЕЛ

В теории чисел довольно часто случается, что благодаря какой-то неожиданной удаче наиболее изящные, новые истины возникают с помощью индукции. — Гаусс[23].

1. Целочисленные прямоугольные треугольники[24]. Треугольник со сторонами 3, 4 и 5 является прямоугольным треугольником, так как

3² + 4² = 5²

Это простейший пример прямоугольного треугольника, стороны которого измеряются целыми числами. Такие «целочисленные прямоугольные треугольники» играли важную роль в истории теории чисел; даже древние вавилоняне открыли некоторые из их свойств.

Вот одна из наиболее очевидных задач, касающаяся таких треугольников:

Существуют ли целочисленные прямоугольные треугольники, гипотенузой которых является данное число π?

Сосредоточим свое внимание на этой задаче. Мы разыскиваем треугольник, гипотенуза которого измеряется данным целым числом n, а катеты какими-то целыми числами x и y, такие, что

n² = x² + y², 0 < y ≤ x < n.

Мы можем подойти к задаче с помощью индукции, и, если только мы не владеем какими-нибудь специальными знаниями, у нас никакого другого пути и нет. Возьмем пример. Выберем n = 12. Итак мы ищем два положительных целых числа x и y, таких, что x ≥ y и

144 = x² + y².

Какие значения может принимать x²? Вот какие:

1, 4, 9, 16, 25, 36, 49, 64, 81, 100, 121.

81

Возможно ли, что x² = 121? Т. е. является ли разность

144 — x² = 144 — 121 = y²

квадратом? Нет, 23 не квадрат. Теперь нужно было бы испытать другие квадраты, но в действительности испытывать слишком много из них нет необходимости. Так как y ≤ x, то

144 = x² + y² ≤ 2x²,

x² ≥ 72,

так что x² = 100 и x² = 81 — единственные остающиеся возможности. Но ни одно из чисел

144 — 100 = 44, 144 — 81 = 63

не является квадратом и отсюда ответ: не существует ни одного целочисленного прямоугольного треугольника с гипотенузой 12.

Рассмотрим подобным же образом гипотенузу 13. Из трех чисел

169 — 144 = 25, 169 — 48, 169 — 100 = 69

квадратом является только одно и, таким образом, существует лишь один целочисленный прямоугольный треугольник с гипотенузой 13:

169 = 144 + 25.

Действуя подобным образом, мы можем при некоторой настойчивости исследовать все числа до данного не слишком высокого предела, например 20. мы находим только пять «гипотенуз» меньших чем 20 — числа 5, 10, 13, 15 и 17:

25	=	16	+	9,
100	=	64	+	36,
169	=	144	+	25,
225	=	144	+	81,
289	=	225	+	64

Между прочим, случаи 10 и 15 не очень интересны. Треугольник со сторонами 10, 8 и 6 подобен более простому треугольнику со сторонами 5, 4 и 3, и это же верно для треугольника со сторонами 15, 12 и 9. остающиеся три прямоугольных треугольника с гипотенузами соответственно 15, 13 и 17 существенно различны; ни один из них не подобен другому.

Мы можем подметить, что все числа 5, 13 и 17 являются нечетными простыми числами. Однако это не все нечетные простые числа до 20; ни одно из других нечетных простых чисел — 3, 7, 11 и 19 — не является гипотенузой. Почему? В чем различие между этими двумя множествами? когда, при каких условиях нечетное простое число является гипотенузой, и когда не является?

82

Это — видоизменение нашего первоначального вопроса. Оно может казаться более многообещающим: во всяком случае, оно является новым. Исследуем его снова с помощью индукции. При небольшой настойчивости мы составим следующую таблицу (черта указывает, что нет прямоугольного треугольника с гипотенузой p).

Нечетное простое число p		Прямоугольные треугольники с гипотенузой p
	3			—
	5	25	=	16 + 9
	7			—
	11			—
	13	169	=	144 + 25
	17	289	=	225 + 64
	19			—
	23			—
	29	841	=	441 + 400
	31			—

Когда простое число является гипотенузой и когда нет? В чем различие между этими двумя случаями? Физик легко мог бы задать себе какие-нибудь очень похожие вопросы. Например, он исследует двойное лучепреломление кристаллов. Некоторые кристаллы действительно обнаруживает двойное лучепреломление, другие нет. Какие кристаллы являются дважды лучепреломляющими, а какие нет? В чем различие между этими двумя случаями?

Физик разглядывает свои кристаллы, а мы разглядываем свои два множества простых чисел[25]:

5, 13, 17, 29, … и 3, 7, 11, 19, 23, 31, …

Хотелось бы отыскать какое-нибудь характеристическое различие между этими двумя множествами. Числа в обоих множествах возрастают неправильными скачками. Посмотрим на длины этих скачков, на последовательные разности:

5		13		17		29	3		7		11		19		23		31
	8		4		12			4		4		8		4		8

Многие из этих разностей равны 4 и, как легко заметить, все они делятся на 4. Числа в первом множестве, начинающемся с 5, при делении на 4 дают остаток 1, имеют вид 4n + 1 с целым n. Числа из второго множества, начинающегося с 3, имеет вид 4n + 3. Могло бы это быть характеристическим различием, которое мы ищем? Если мы с самого начала не отбросим этой возможности, то придем к следующему предположению: простое число вида 4n + 1 является гипотенузой в точности одного целочисленного прямоугольного треугольника; простое число вида 4n + 3 не является гипотенузой ни одного такого треугольника.

83

2. Суммы квадратов. Задача о целочисленных прямоугольных треугольниках, одним аспектом которой мы только что занимались (в § 1), играла, как мы сказали, важную роль в истории теории чисел. Она приводит в действительности к многим дальнейшим вопросам. Какие вообще числа, квадраты или нет, могут быть разложены в сумму двух квадратов? Что можно сказать о числах, которые не могут быть разложены в сумму двух квадратов? Возможно, они разложимы в сумму трех квадратов; но что можно сказать о числах, неразложимых в сумму трех квадратов?

Мы могли бы продвигаться беспредельно, но, и это в высшей степени замечательно, мы в этом не нуждаемся. Баше де Мезириак (автор первой печатной книги о математических развлечениях) заметил, что любое (т. е. положительное целое) число есть или квадрат, или сумма двух, трех или четырех квадратов. Он не претендовал на доказательство. От[26] нашел намеки, приводящие к этому утверждению в некоторых задачах Диофанта и убедился, что оно верно для всех чисел до 325.

Короче говоря, утверждение Баше было всего лишь предположением, найденным индуктивно. Мне кажется, что главным его достижением была постановка вопроса: СКОЛЬКО квадратов нужно, чтобы представить все целые числа? Раз этот вопрос ясно поставлен, не представляет особых трудностей найти ответ с помощью индукции. Мы составляем таблицу, начиная с

1	=	1,
2	=	1 + 1,
3	=	1 + 1 + 1,
4	=	4,
5	=	4 + 1,
6	=	4 + 1 + 1,
7	=	4 + 1 + 1 + 1,
8	=	4 + 4,
9	=	9,
10	=	9 + 1

Этим предположение подтверждается для чисел до 10. Только число 7 требует четырех квадратов; другие представимы с помощью одного, двух или трех. Баше продолжил таблицу для чисел до 325 и нашел много чисел, требующих четырех квадратов, и ни одного, требующего больше. Такие индуктивные доводы, по-видимому, убедили его, по крайней мере до некоторой степени, и он опубликовал свое утверждение. Ему повезло. Его предположение оказалось верным, и, таким образом, ему принадлежит открытие «теоремы о четырех квадратах», которую мы можем сформулировать и в такой форме: Уравнение

n = x² + y² + z² + w²,

84

где n — любое данное положительное целое число, имеет решение, в котором x, y, z и w являются неотрицательными целыми числами.

Разложение числа в сумму квадратов можно рассматривать и с других точек зрения. Так, мы можем исследовать число решений уравнения

n = x² + y²

в целых числах x и y. Мы можем допускать только положительные целые числа или все целые числа, положительные, отрицательные или 0. если мы выберем последнее понимание задачи и возьмем в качестве примера n = 25, то найдем 12 решений уравнения

25 = x² + y²

а именно следующие:

25 = 5² + 0² = (—5)² + 0² = 0² + 5² = 0² + (—5)² =4² + 3² = (—4)² + 3² = 4² + (—3)² =

= (—4)² + (—3)² = 3² + 4² = (—3)² + 4² = 3² + (—4)² = (—3)² + (—4)².

Между прочим, эти решения имеют интересную геометрическую интерпретацию, но нам нет необходимости ее здесь рассматривать. См. пример 2.

3 О сумме четырех нечетных квадратов. Из многих задач, относящихся к суммам квадратов, я выбираю задачу, которая выглядит настолько искусственной, но окажется чрезвычайно поучительной.

Пусть u обозначает положительное нечетное число. Исследовать индуктивно число решений уравнения

4u = x² + y² + z² + w²

в положительных нечетных числах x, y, z и w.

Например, если u = 1, то мы имеем уравнение

4 = x² + y² + z² + w²

и, очевидно, имеется всего лишь одно решение x = y =z = w = 1.

В самом деле,

x = —1, y = 1, z = 1, w = 1

или

x = 2, y = 0, z = 0, w = 0

мы не рассматриваем как решения, так как предполагаем, что x, y, z и w могут быть только положительными нечетными числами. Если u = 3, то уравнение имеет вид

12 = x² + y² + z² + w²

85

и следующие решения:

x = 3, y = 1, z = 1, w = 1

x = 1, y = 3, z = 1, w = 1

являются различными.

Для того чтобы подчеркнуть ограничение, наложенное на значения x, y, z и w, мы будем избегать термина «решение» и вместо него пользоваться более специфическим описанием[27]: представление числа 4u в виде суммы четырех нечетных квадратов». Так как это описание длинно, мы будем его различными способами сокращать, иногда даже до одного слова «представление».

4. Исследование примера. Для того чтобы вникнуть в смысл нашей задачи, рассмотрим пример. Выберем u = 25. Тогда 4u = 100, и мы должны найти все представления числа 100 в виде суммы четырех нечетных квадратов. Какие нечетные квадраты пригодны для этой цели? Следующие:

1, 9, 25, 49, 81.

Если 81 является одним из четырех квадратов, сумма которых равна 100, то сумма трех других должна быть

100 — 81 = 19.

Нечетными квадратами, меньшими, чем 19, являются лишь 1 и 9 и, очевидно, для представления 19 в виде суммы 3 нечетных квадратов, если члены расположены в порядке убывания, имеется единственная возможность. Мы получаем

100 = 81 + 9 + 9 + 1.

Подобным же образом находим

100 = 49 + 49 + 1 + 1,

100 = 49 + 25 + 25 + 1,

100 = 25 + 25 + 25 + 25.

Действуя систематически, отщепляя сначала наибольший квадрат, мы можем убедиться, что исчерпали все возможности, при условии, что 4 квадрата расположены в порядке убывания (или, точнее, в порядке невозрастания). Но если мы примем в расчет, как нам и надлежит, все расположения членов, ото существует больше возможностей. Например,

100 = 49 + 49 + 1 + 1 = 49 + 1 + 49 + 1 = 1 + 49 + 49 + 1 = 1 + 49 +1 + 49 = 1 + 1 + 49 + 49.

86

Эти шесть сумм имеют одни и те же члены, но порядок членов различен; в соответствии с постановкой нашей задачи они должны рассматриваться как 6 различных представлений; одно представление

100 = 49 + 49 + 1 + 1

с невозрастающими членами является источником пяти других представлений, а всего шести представлений. Подобным же образом имеем:

Невозрастающие члены				Число расположений
81 +	9 +	9 +	1		12
49 +	49 +	1 +	1		6
49 +	25 +	25 +	25		12
25 +	25 +	25 +	25		1

Подводя итог, мы находим в нашем случае, когда u = 25 и 4u = 100, количество представлений числа 4u = 100 в виде суммы 4 нечетных квадратов:

12 + 6 + 12 + 1 = 31.

5. Составление таблицы наблюдений. Частный случай u = 25, где 4u = 100 и число представлений равно 31, ясно показывает нам смысл задачи. Мы можем теперь систематически изучить простейшие случаи, u = 1? 3? 5, … до u = 25. Составим таблицу (см. стр. 87, читателю следует самому составить таблицу или по крайней мере проверить несколько строк).

6. Каково правило? Существует ли какой-нибудь закон, который мы могли бы распознать, какая-либо простая связь между нечетным числом u числом различных представлений числа 4u в виде суммы четырех нечетных квадратов?

Этот вопрос — ядро нашей задачи. Мы должны на него ответить на основании наблюдений, собранных и сведенных в таблицу в предыдущем параграфе. Мы находимся в положении натуралиста, пытающегося извлечь из своих экспериментальных данных какое-нибудь правило, какую-нибудь общую формулу. Экспериментальный материал, имеющийся к этому моменту в нашем распоряжении, состоит из двух параллельных рядов чисел:

1	3	5	7	9	11	13	15	17	19	21	23	25
1	4	6	8	13	12	14	24	18	20	32	24	31

Первый ряд состоит из последовательных нечетных чисел, но какое правило управляет вторым рядом?

Когда мы пытаемся ответить на этот вопрос, наше первое чувство может быть близко к отчаянию. Этот второй ряд кажется совершенно неправильным, нас озадачивает его сложное происхождение, мы едва ли можем надеяться найти какое-нибудь правило. Однако если мы забудем

87

Таблица 1

u	4u	Невозрастающие слагаемые				Расположения	Представления
1	4	1 +	1 +	1 +	1	1	1
3	12	9 +	1 +	1 +	1	4	4
5	20	9 +	9 +	1 +	1	6	6
7	28	25 +	1 +	1 +	1	12	13
		9 +	9 +	9 +	1	1
9	36	25 +	9 +	1 +	1	12	12
		9 +	9 +	9 +	9	1
11	44	25 +	9 +	9 +	1	12	12
13	52	49 +	1 +	1 +	1	4	14
		25 +	25 +	1 +	1	6
		25 +	9 +	9 +	9	4
15	60	49 +	9 +	1 +	1	12	24
		25 +	25 +	9 +	1	12
17	68	49 +	9 +	9 +	1	12	18
		25 +	25 +	9 +	9	6
19	76	49 +	25 +	1 +	1	12	20
		49 +	9 +	9 +	9	4
		25 +	25 +	25 +	1	4
21	84	81 +	1 +	1 +	1	4	32
		49 +	25 +	9 +	1	24
		25 +	25 +	25 +	1	4
23	92	81 +	9 +	1 +	1	12	24
		49 +	25 +	9 +	9	12
25	100	81 +	9 +	9 +	1	12	31
		49 +	49 +	1 +	1	6
		49 +	25 +	25 +	1
		25 +	25 +	25 +	25

о его сложном происхождении и сосредоточим свое внимание на том, что находится перед нами, то достаточно легко заметить одно обстоятельство. Довольно часто случается, что член второго ряда превосходит соответствующий член первого ряда ровно на ндну единицу. Выделяя эти случаи жирным шрифтом в первом ряду, мы можем представить наш экспериментальный материал следующим образом:

1	3	5	7	9	11	13	15	17	19	21	23	25
1	4	6	8	13	12	14	24	18	20	32	24	31

Наше внимание привлекают числа, напечатанные жирным шрифтом. Нетрудно их узнать: они простые. Действительно, это все простые числа, имеющиеся в первом ряду нашей таблицы. Это замечание, если мы припомним происхождение нашего ряда, может показаться очень удивительным. Мы рассматривали квадраты, мы никоим образом не касались простых чисел. Не странно ли, что в нашей задаче какую-то роль играют простые числа? Трудно избежать впечатления, что наше наблюдение имеет важное значение, что за ним кроется что-то замечательное.

88

Что же можно сказать о числах из первого ряда, не напечатанных жирным шрифтом? Они являются нечетными числами, но не простыми. Первое, 1, единица, другие — составные:

9 = 3 × 3, 15 = 3 × 5, 21 = 3 × 7, 25 = 5 × 5.

Какова природа соответствующих чисел во втором ряду?

Если нечетное число u простое, то соответствующее число равно u + 1; если u не простое, то соответствующее число не равно u + 1. Это мы уже заметили. Мы можем прибавить одно маленькое замечание. Если u = 1, то соответствующее число также 1, и, таким образом, оно меньше, чем u + 1, но во всех других случаях, когда u не простое, соответствующее число больше, чем u + 1. Иными словами, число, соответствующее u, меньше, равно или больше, чем u + 1 в соответствии с тем, является ли u единицей, простым или составным числом. Существует какая-то закономерность.

Сосредоточим свое внимание на составных числах в верхней строке и соответствующих числах в нижней

3 × 3	3 × 5	3 × 3	5 × 5
13	24	32	31

Что-то странное. Квадраты в первой строке соответствуют простым числам во второй. Однако у нас слишком мало наблюдений; вероятно, нам не следует придавать этому замечанию слишком большого значения. Все же верно, что, наоборот, под составными числами в первой строке, не являющимися квадратами, мы находим во второй строке числа, не являющиеся простыми

3 × 5	3 × 7
4 × 6	4 × 8

Снова что-то странное. Каждый множитель во второй стоке превосходит соответствующий множитель в первой строке ровно на ндну единицу. Однако у нас слишком мало наблюдений; нам лучше не придавать этому замечанию слишком большого значения. Все же наше замечание обнаруживает какой-то параллелизм с предыдущим замечанием. Мы подметили раньше

p

p + 1

и мы подметили теперь

pq

(p + 1)(q + 1),

где p и q простые. Существует какая-то закономерность.

Возможно, мы увидим это яснее, если напишем число, соответствующее pq, иначе:

(p + 1)(q + 1) = pq + p + q + 1.

89

Что же мы можем здесь увидеть? Что это за числа pq, p, q, 1? Как бы то ни было, случаи

9	25
13	31

остаются необъясненными. Действительно, числа, написанные под 9 и 25, как мы уже заметили, соответственно, больше, чем 9 + 1 и 25 + 1:

13 = 9 + 1 + 3, 31 = 25 + 1 + 5.

Что это за числа?

Теперь достаточно лишь небольшой искры и нам может удастся[28] соединить наши отрывочные замечания в стройное целое, наши разрозненные указания в эффектную картину полного соответствия:

p	pq	9	25	1
p + 1	pq + p + q + 1	9 + 3 + 1	25 + 5 + 1	1

ДЕЛИТЕЛИ! Вторая строка указывает делители чисел первой строки. Это может оказаться разыскиваемым правилом и открытием, настоящим открытием:

Каждому числу в первой строке соответствует сумма его делителей.

И таким образом мы пришли к предположению, быть может, к одной из тех «наиболее изящных новых истин» Гаусса:

Если u — нечетное число, то число представлений числа 4u в виде суммы четырех нечетных квадратов равно сумме делителей u.

7. Природа индуктивного открытия. Просматривая предыдущие параграфы (от 3 до 6), мы можем найти много вопросов, нуждающихся в ответе.

Что мы получили? Не доказательство, даже не тень доказательства, а всего лишь предположение: простое описание фактов в пределах нашего экспериментального материала и некоторую надежду, что это описание можно применить и за пределами нашего экспериментального материала.

Как мы получили наше предположение? В основном тем же способом, каким обычные люди или ученые, работающие в какой-нибудь нематематической области получают свои. Мы собрали относящиеся к вопросу наблюдения, исследовали и сравнили их, подметили отрывочные закономерности, колебались, спотыкались, и в конце концов нам удалось _соединить разрозненные детали в явно многозначительное целое. Совершенно подобным же образом археолог по нескольким разрозненным буквам на стертом камне может восстановить целую надпись или палеонтолог по немногим окаменевшим

90

костям вымершего животного может восстановить его существенные черты. В нашем случае многозначительное целое появилось в тот самый момент, когда мы осознали подходящее объединение понятие (делители).

8. О природе индуктивных доводов. Остается еще несколько вопросов.

Насколько сильны эти доводы? Ваш вопрос является неполным. Вы имеете, конечно, в виду индуктивные доводы для нашего предположения, сформулированного в § 6, которые мы можем вывести из табл. 1 § 5; это понятно. Однако что вы понимаете под словом «сильны»? Доводы сильны, если они убедительны; они убедительны, если они кого-нибудь убеждают. Однако вы не сказали, кого они должны были бы убеждать — меня или вас или Эйлера или начинающего или кого-нибудь еще?

Лично я нахожу доводы довольно убедительными. Я чувствую уверенность, что Эйлер думал бы о них очень благоприятно (я упоминаю Эйлера потому, что он очень близко подходил к открытию нашего предположения; см. пример 6.24). Я думаю, что начинающий, который кое-что знает о делимости чисел, также нашел бы доводы довольно убедительными. Мой коллега, превосходный математик, который, однако, не был знаком с этим уголком теории чисел, нашел доводы «убедительными на сто процентов».

Я не интересуюсь субъективными впечатлениями. Какова точная, объективно оцениваемая степень разумной веры, оправдываемая индуктивными доводами?[29] Вы даете мне одно (A), не даете мне другого (B) и спрашиваете у меня о третьем (C).

(A) Вы даете мне только лишь индуктивные доводы: предположение было подтверждено в первых тринадцати случаях для чисел 4, 12, 20, …, 100. Это совершенно ясно.

(B) Вы желаете, чтобы я оценил степень разумной веры, оправдываемую этими доводами. Однако такая вера должна зависеть если не от капризов и темперамента, то от знаний человека, воспринимающего доводы. Он может знать доказательство предполагаемой теоремы или противоречащий пример, подрывающий ее. В этих двух случаях степень его веры, уже твердо установления, не изменится под влиянием индуктивных доводов. Однако если он знает что-нибудь, что очень близко подходит к полному доказательству или к полному опровержению теоремы, то его вера еще способна измениться и на нее окажут воздействие полученные здесь индуктивные доводы, хотя в соответствии с характером знаний, которые он имеет, из этих доводов будут вытекать различные степени веры. Поэтому, если вы хотите определенного ответа, вам следовало бы указать определенный уровень знаний, на основе которого должны были бы оцениваться предложенные индуктивные доводы (A). Вы должны дать мне определенный набор относящихся к рассматриваемому вопросу

91

известных фактов (возможно, подробный список известных элементарных предложений из теории чисел).

(C) Вы желаете, чтобы я точно оценил степень разумной веры, оправдываемую индуктивными доводами. Быть может, мне следует дать ее вам в процентах «полной веры»? (Мы можем условиться называть «полной верой» степень веры, оправдываемую полным математическим доказательством рассматриваемой теоремы). Не хотите ли вы услышать, что данные доводы оправдывают веру, составляющую 99% или 2,875% или 0,000001% «полной веры»?

Короче говоря, вы желаете, чтобы я решил задачу:

Пусть даны (A) индуктивные доводы и (B) определенный набор известных фактов и предложений; вычислить (C) процент полной веры, разумно вытекающий из (A) и (B).

Решить эту задачу — означало бы сделать гораздо больше, чем в моих силах. Я не знаю никого, кто смог бы это сделать, и никого, кто отважился бы это сделать[30]. Я знаю некоторых философов, которые обещают сделать что-то в этом роде в чрезвычайной общности. Однако, встретив конкретную задачу, они уклоняются и увиливают и находят тысячу отговорок, объясняющих, почему нельзя решить именно эту задачу.

Возможно, эта задача является одной из тех типичных философских задач, о которых вы можете много говорить вообще и даже проявлять подлинную заинтересованность, но которые превращаются в ничто, когда вы снижаете их до конкретных условий.

Могли бы вы сравнить настоящий случай индуктивного умозаключения с каким-нибудь другим знакомым случаем и таким образом прийти к разумной оценке силы доводов? Сравним индуктивные доводы в пользу нашего предположения с доводами Баше в пользу его предположения.

Вот предположение Баше: для n = 1, 2, 3, … уравнение

n = x² + y² + z² + w²

имеет по крайней мере одно решение в неотрицательных целых числах x, y, z и w. Он убедился, что это предположение верно для n = 1, 2, 3, …, 325. (См. § 2, в частности, короткую таблицу.)

Вот наше предположение: для данного нечетного u число решений уравнения

4u = x² + y² + z² + w²

в положительных нечетных числах x, y, z, и w равно сумме делителей числа u. Мы убедились, что это предположение верно для u = 1, 3, 5, 7, 25 (13 случаев). (См. §§ 3—6)

Я сравню эти два предположения и индуктивные доводы, даваемые их соответственными подтверждениями, в трех отношениях.

Число подтверждений. Предположение Баше было подтверждено в 325 случаях, наше предположение — только в 13 случаях. Преимущество в этом отношении явно на стороне Баше

92

Точность предсказания. Предположение Баше предсказывает, что число решений ≥ 1; наше — предсказывает, что число решений в точности равно такой-то и такой-то величине. Очевидно, разумно допустить, как я полагаю, что подтверждение более точного предсказания имеет больше веса, чем подтверждение менее точного предсказания. В этом отношении преимущество явно на нашей стороне.

Соперничающие предположения. Предположение Баше относится к максимальному числу квадратов, скажем, M, необходимому для представления произвольного положительного целого числа в виде суммы квадратов. Действительно, предположение Баше утверждает, что M = 4. Я не думаю, что Баше a puiori имел какое-нибудь основание предпочесть M = 4, скажем, M = 5 или любому другому значению, например M = 6 или M = 7; a puiori не исключено даже M = ∞. (естественно, M = ∞ означало бы, что существуют все бо́льшие и бо́льшие целые числа, требующие все большего и большего числа квадратов. На первый взгляд, M = ∞ могло бы казаться наиболее вероятным предположением.) Короче говоря, у предположения Баше есть много очевидных соперников. А у нашего нет ни одного. Когда мы рассматривали неправильную последовательность чисел представления (§ 6), у нас было впечатление, что мы можем оказаться не в состоянии найти никакого правила. Теперь мы все-таки нашли замечательно ясное правило. Нам трудно надеяться найти какое-нибудь другое правило.

Может оказаться трудным выбрать невесту, если для выбора имеется много привлекательных юных леди: если же поблизости есть всего лишь одна подходящая девушка, то решение может прийти намного быстрее. Мне кажется, что наше отношение к предположениям отчасти сходно. При прочих равных условиях предположение, имеющее много очевидных соперников, принять труднее, чем предположение, не имеющее соперников. Если вы думаете так же, как и я, то вы должны найти, что в этом отношении преимущество на стороне нашего предположения, а не на стороне предположения Баше.

Пожалуйста, заметьте, что доводы в пользу предположения Баше сильнее в одном отношении, а доводы в пользу нашего предположения сильнее в других отношениях, и не задавайте вопросов, на которые нельзя ответить.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ IV

1. Обозначения. Мы предполагаем, что n и k — положительные целые числа и рассматриваем диофантово уравнение

n = x₁² + x₂² + … + x_k².

Мы говорим, что два решения x₁, x₂, …, x_k и x′₁, x′₂, …, x′_k равны в том и только в том случае, если x₁ = x′₁, x₂ = x′₂, …, x_k = x′_k. Если мы допускаем

93

для x₁, x₂…, x_k, все целые числа, положительные, отрицательные или нуль, то число решений мы обозначаем символом R_k(n). Если мы допускаем только положительные нечетные числа, то число решений обозначаем символом S_k(n). Эти обозначения играют важную роль в большей части следующих задач.

Предположение Баше (§ 2) выражается в этих обозначениях неравенством

R₄(n) > 0 для n = 1, 2, 3, …

Предположение, открытое нами в § 6 утверждает, что S₄(4(2n —1)) равно сумме делителей числа 2n —1 для n = 1, 2, 3, ….

Найдите R₂(25) и S₃(11).

2. Пусть x и y — прямоугольные координаты на плоскости. Точки, для которых и x, и y суть целые числа, называются «точками решетки» на плоскости. Точки решетки в пространстве определяются аналогично.

Найдите геометрическую интерпретацию R₂(n) и R₃(n) в терминах точек решетки.

3. Выразите предположение, с которым мы встретились в § 1, пользуясь символом R₂(n).

4. Когда нечетное число является суммой двух квадратов? Попытайтесь ответить на этот вопрос с помощью индукции, исследуя таблицу

3	=	—
5	=	4 + 1
7	=	—
11	=	—
13	=	9 + 4
17	=	16 + 1
19	=	—
23	=	—
29	=	25 + 4
31	=	—

Продолжите, если необходимо, эту таблицу и сравните ее с таблицей § I.

5. Могли бы вы путем математической дедукции подтвердить какую-нибудь часть вашего ответа к примеру 4, полученного с помощью индукции? После такого подтверждения не было ли бы разумно изменить вашу веру в предположение?

6. Проверьте предположение Баше (§ 2) для чисел до 30 включительно. Какие числа действительно требуют четырех квадратов?

7. Пусть a², b², c² и d² обозначают четыре различных нечетных квадрата. Чтобы лучше понять табл. I в § 5, рассмотрите суммы

(1) a² + b² + c² + d²,

(2) a² + a² + b² + c²,

(3) a² + a² + b² + b²,

(4) a² + a² + a² + b²,

(5) a² + a² + a² + a²,

Сколько различных представлений (в смысле § 3) вы можете получить из каждой суммы с помощью перестановки членов?

8. Число представлений числа 4u в виде суммы четырех нечетных квадратов нечетно в том и только в том случае, если u и есть квадрат. (Следуя обозначениям § 3, мы предполагаем, что u нечетно.) Докажите это утверждение и покажите, что оно находится в согласии с предположением § 6. Какое влияние оказывает это замечание на вашу веру в это предположение?

94

9. Пусть теперь a, b, c и d обозначают четыре различные положительные целые числа (четные и нечетные). Рассмотрите пять сумм, упомянутых в примере 7, а также следующие:

(6)	a^2 + b^2 + a^2,	(9)	a^2 + b^2
(7)	a^2 + a^2 + b^2,	(10)	a^2 + a^2,
(8)	a^2 + a^2 + a^2,	(11)	a^2.

Найдите в каждом из этих одиннадцати случаев взнос в R₄(n). Все возможные представления нужно выводить из каждой суммы с помощью следующих очевидных операций: прибавлять 0² столько раз, сколько необходимо, чтобы довести число членов до 4, изменять порядок и заменять несколько (или ни одного, или все) чисел a, b, c, d соответственно числами — a, — b, — c, —d (проверьте примеры в табл II.)

Таблица II

n	Невозрастающие слагаемые	Представления	R4(n)/8.
1	1	4 × 2	1
2	1 + 1	6 × 4	3
3	1 + 1 + 1	4 × 8	4
4	4	4 × 2	3
	1 + 1 + 1 + 1	1 × 16
5	4 + 1	12 × 4	6
6	4 + 1 + 1	12 × 8	12
7	4 + 1 + 1 + 1	4 × 16	8
8	4 + 4	6 × 4	3
9	9	4 × 2	13
	4 + 4 + 1 + 1	12 × 8
10	9 + 1	12 × 4	18
	4 + 1 + 1 + 1	6 × 16
11	9 + 1 + 1	12 × 8	12
12	9 + 1 + 1 + 1	4 × 16	12
	4 + 4 + 4	4 × 8
13	9 + 4	12 × 4	14
	4 + 4 + 4 + 1	4 × 16
14	9 + 4 + 1	24 × 8	24
15	9 + 4 + 1 + 1	12 × 16	24
16	16	4 × 2	3
	4 + 4 + 4 + 4	1 × 16
17	16 + 1	12 × 4	18
	9 + 4 + 4	12 × 8
18	16 + 1 + 1	12 × 8	39
	9 + 9	6 × 4
	9 + 4 + 4 + 1	12 × 16
19	16 + 1 + 1 + 1	4 × 16	20
	9 + 9 + 1	12 × 8
20	16 + 4	12 × 4	18
	9 + 9 + 1 + 1	6 × 16
21	16 + 4 + 1	24 × 8	32
	9 + 4 + 4 + 4	4 × 16
22	16 + 4 + 1 + 1	12 × 16	36
	9 + 9 + 4	12 × 8
23	9 + 9 + 4 + 1	12 × 16	24

95

Продолжение таблицы II

n	Невозрастающие слагаемые	Представления	R4(n)/8.
24	16 + 4 + 4	12 × 8	12
25	25	4 × 2	31
	16 + 9	12 × 4
	16 + 4 + 4 + 1	12 × 16
26	25 + 1	12 × 4	42
	16 + 9 + 1	24 × 8
	9 + 9 + 4 + 4	6 × 16
27	25 + 1 + 1	12 × 8	40
	16 + 9 + 1 + 1	12 × 16
	9 + 9 + 9	4 × 8
28	25+ 1 + 1 + 1	4 × 16	24
	16 + 4 + 4 + 4	4 × 16
	9 + 9 + 9 + 1	4 × 16
29	25 + 4	12 × 4	30
	16 + 9 + 4	24 × 8
30	25 + 4 + 1	24 × 8	72
	16 + 9 + 4 + 1

Таблица III

n	R4(n)/8	R8(n)/16	S8(8n)	S4(4(2n —1))	2n —1
1	1	1	1	1	1
2	3	7	8	4	3
3	4	28	28	6	5
4	3	71	64	8	7
5	6	126	126	13	9
6	12	196	224	12	11
7	8	344	344	14	13
8	3	583	512	24	15
9	13	757	757	18	17
10	18	882	1008	20	19
11	12	1332	1332	32	21
12	12	1988	1792	24	23
13	14	2198	2198	31	25
14	24	2408	2752	40	27
15	24	3528	3528	30	29
16	3	4679	4096	32	31
17	18	4914	4914	48	33
18	39	5299	6056	48	35
19	20	6860	6860	38	37
20	18	8946	8064	56	39

10. Индуктивно исследуйте число решений уравнения n = x² + y² + z² + w² в целых числах x, y, z и w, положительных, отрицательных или 0. начните с построения таблицы, аналогичной табл. I

96

11 (продолжение). Попытайтесь воспользоваться методом или результатом § 6.

12 (продолжение). Руководствуясь аналогией с § 6 или вашим наблюдением табл II, выделите подходящие классы целых чисел и исследуйте каждый класс сам по себе.

13 (продолжение). Сконцентрируйте свое внимание на наиболее неподдающемся вашим усилиям классе.

14 (продолжение). Попытайтесь суммировать все отрывочные закономерности и выразите закон в одном предложении.

15 (продолжение). Проверьте найденное плавило в первых стрех случаях, не содержащихся в табл II.

16. Найдите R₈(5) и S₈(40).

17. Проверьте по крайней мере две строки в табл. III стр. 95, еще не приведенные в табл. I и II.

18. Пользуясь табл. III, индуктивно исследуйте R₈(n) и S₈(n).

19 (продолжение). Попытайтесь воспользоваться методом или результатом § 6 и примеров 10—15.

20 (продолжение). Руководствуясь аналогией или наблюдением, выделите подходящие классы целых чисел и исследуйте каждый класс сам по себе.

21 (продолжение). Попытайтесь обнаружить ключ в наиболее доступном случае.

22 (продолжение). Попытайтесь найти какое-нибудь объединяющее понятие, которое могло бы суммировать отрывочные закономерности.

23 (продолжение). Попытайтесь выразить закон в одном предложении.

24. Какие целые числа могут и какие не могут быть выражены в виде 3x + 5y, где x и y — неотрицательные целые числа.

25. Попытайтесь догадаться, по какому закону составлена следующая таблица:

a	b	Последнее целое число, не выражающееся в виде ax + by
2	3	1
2	5	3
2	7	5
2	9	7
3	4	5
3	5	7
3	7	11
3	8	13
4	5	11
5	6	19

Подразумевается, что x и y — неотрицательные целые числа. Проверьте несколько строк и, если необходимо, продолжите таблицу. (Проследите изменения, происходящие в последнем столбце, когда изменяется лишь одно из двух чисел a и b.)

26. Опасности индукции. Индуктивно исследуйте следующие утверждения:

(1) (n — 1)! + 1 делится на n, когда n — простое число, но не делится на n, когда n — составное число.

(2) 2^n—1 — 1 делится на n, когда n — нечетное простое число, но не делится на n, когда n — составное число.

V. РАЗНЫЕ ПРИМЕРЫ ИНДУКЦИИ

Когда вы убедитесь, что теорема верна, вы начинаете ее доказывать. — Традиционный профессор математики[25][26].

1. Разложения. Сталкиваясь с разного рода задачами, мы нуждаемся в определенном типе индуктивных рассуждений. В различных областях математики встречаются некоторые задачи, требующие индуктивных рассуждений типичного характера. Настоящая глава несколькими примерами иллюстрирует этот тезис. Мы начинаем с относительно простого примера.

Разложить по степеням x функцию 1/(1 — x + x²).

Эта задача может быть решена многими способами. Нижеследующее решение несколько громоздко, но оно основано на правильном принципе и может естественно прийти в голову умному начинающему, который знает немного, но все же по крайней мере знает сумму геометрической прогрессии:

В нашей задаче есть возможность воспользоваться этой формулой:

=

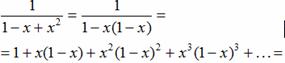
1

+

x

—

x^2

+

+

x^2

—

2x^3

+

x^4

+

+

x^3

—

3x^4

+

3x^5

—

x^6

+

+

x^4

—

4x^5

+

6x^6

—

4x^7

+

x^8

+

+

x^5

—

5x^6

+

10x^7

—

10x^8

+…

+

x^6

—

6x^7

+

15x^8

—…

+

x^7

—

7x^8

+…

+

x^8

—…

…

=

1

+

x

—

x^3

—

x^4

+

x^6

+

x^7

98

Результат поразителен. Любой отличный от нуля коэффициент имеет или значение 1 или значение — 1. последовательность коэффициентов, по-видимому, обнаруживает некоторую закономерность, которая станет более очевидной, если мы вычислим еще несколько членов:

Периодичность! Последовательность коэффициентов оказывается периодической с периодом 6:

1, 1, 0, — 1, — 1, 0 | 1, 1, 0, — 1, —1, 0 | 1, 1, …

Мы, естественно, ожидаем, что наблюдаемая периодичность продолжится и за пределами наших наблюдений. Но это — индуктивное заключение или всего лишь догадка, к которой нам следовало бы отнестись с должным недоверием. Эта догадка, однако, основана на фактах и поэтому заслуживает серьезного исследования. Исследовать ее, помимо всего прочего, значит выразить ее по-другому. Существует интересный способ выразить иначе наше предположение:

Теперь мы легко можем заметить в правой части равенства две геометрические прогрессии с одним и тем же знаменателем — x³, суммы которых мы можем найти. И, таким образом, предположение сводится к равенству

которое, конечно, верно. Мы доказали наше предположение.

Наш пример, несмотря на свою простоту, во многих отношениях типичен. Если нам нужно разложить данную функцию, мы часто можем без большого труда получить первые несколько коэффициентов. Рассматривая эти коэффициенты, мы должны попытаться, как мы здесь и сделали, угадать закон, управляющий разложением. Угадав закон, мы должны попытаться, как мы здесь и сделали, его доказать. Может оказаться очень выгодным, как это здесь и оказалось, провести доказательство в обратном направлении, исходя из подходящей ясной формулировки предположения.

Между прочим, наш пример является весьма благодарным (что также типично). Он приводит к любопытному соотношению между биномиальными коэффициентами.

Не лишне будет добавить, что задача разложения данной функции в ряд возникает в различных областях математики. См следующий параграф, а также примеры и примечания к гл. 6 наш пример является весьма благодарным (что также типично). Он приводит к любопытному соотношению между биномиальными коэффициентами.

Не лишне будет добавить, что задача разложения данной функции в ряд возникает в различных областях математики. См следующий параграф, а также примеры и примечания к гл. VI.

99

2. Приближения[27]. Пусть E обозначает длину дуги эллипса с полуосями a и b. Для E обозначает длину дуги эллипса с полуосями a и b. Для E не существует простого выражения через a и b, но было предложено несколько приближенных выражений, среди которых следующие два являются, пожалуй, наиболее очевидными:

P = π(a + b), P' = 2π(ab)^½,

P — приближенное, P' — другое приближенное, E — точное выражение для одной и той же величины — длины дуги эллипса. Когда a совпадает с b, эллипс становится окружностью и как P, так и P' совпадают с E.

Насколько хорошо P и P' приближают E, когда a отлично от b? Какое из них ближе к истине, P или P'? вопросы этого рода часто возникают во всех областях прикладной математики, и существует общепринятый способ подхода к ним, который мы в общих чертах опишем следующим образом. Разложите (P — E)/E, относительную погрешность приближения, по степеням подходящей малой величины и основывайте ваше суждение на начальном (первом отличном от нуля) члене разложения.

Посмотрим, что тол означает и как этот прием осуществляется в применении к нашему случаю. Сначала нам нужно выбрать «подходящую малую величину». Испытаем ε, эксцентриситет эллипса, определяемый формулой

a мы считаем большой, а b малой полуосью. Когда a превращается в b, а эллипс в окружность, ε обращается в нуль. Когда эллипс не очень отличается от окружности, ε мало́. Разложим поэтому относительную погрешность по степеням ε. Мы получим (опуская здесь детали)

Мы вычислили только начальный член, который в обоих случаях имеет порядок 4, содержит ε⁴. В обоих разложениях мы не выписали члены высшего порядка, содержащие ε⁵, ε⁶, … Когда ε очень мало (бесконечно мало), т. е. когда эллипс почти круглый, невыписанные члены по сравнению с начальными членами незначительны. Поэтому для почти круглого эллипса P ближе к истинному значению E, чем P'. (Действительно, отношение погрешностей стремится к 1 : 3, когда ε стремится к нулю.) И P и P' приближают E снизу:

E > P > P'.

100

Все это имеет место для очень малого ε, для почти круглых эллипсов. Мы еще не знаем, какая часть этих результатов остается справедливой, когда ε не так мало. Фактически в данный момент мы знаем только предельные соотношения, справедливые при ε → 0. Мы еще ничего определенного не знаем о погрешностях наших приближений, когда ε = 0,5 или ε = 0,1. Конечно, то, что нам нужно на практике, это именно информация о таких конкретных случаях.

Практики при таких обстоятельствах проверяют свои формулы численно. Мы можем последовать за ними, но какой случай нам нужно было бы проверить сначала? Рекомендуется не позабыть крайние случаи. Эксцентриситет ε меняется между крайними значениями 0 и 1. Когда ε = 0, b = a и эллипс превращается в окружность. Однако теперь мы знаем этот случай довольно хорошо, поэтому обратимся лучше к другому крайнему случаю. Когда ε = 1, b = 0, эллипс превращается в прямолинейный отрезок длины 2a, а длина его дуги равна 4a. Мы имеем

E = 4a, P = πa, P' = 0, когда ε = 1,

Пожалуй, стоит отметить, что в обоих крайних случаях, как для ε = 1, так и для очень малого E > P > P'. Справедливы ли эти неравенства для любого ε?

Для второго неравенства ответ нетруден. Действительно, для a > b имеем

P = π(a + b) > 2π(ab)^½ = P',

так как это эквивалентно неравенству

(a + b)² > 4ab,

или

(a + b)² > 0.

Сосредоточим свое внимание на остающемся вопросе. Всегда ли справедливо неравенство E > P? Естественно предположить, что то, что мы нашли верным в крайних случаях (ε мало и ε = 1), остается верным и в промежуточных случаях (для всех значений между 0 и 1). Наше предположение не подкрепляется большим числом наблюдений, но оно подкрепляется аналогией. На подобный же вопрос ( относительно P > P'), который был задан одновременно и опирался на подобные же основания, ответ был утвердительным.

Проверим какой-нибудь случай численно. Мы немного больше знаем о случае, когда ε близко к 1. выберем для ε простое значение, более близкое к 1, чем к 0: a = 5, b = 3, ε = 4/5. Для этого ε (пользуясь соответствующими таблицами) находим

E = 2π × 4,06275, P = 2π × 4,00000.

101

Неравенство E > P подтверждается. Это подтверждение нашего предположения идет с новой стороны, из другого источника и потому имеет некоторый вес. Отметим также, что

((P — E)/E = — 0, 0155, ε⁴/64 = — 0, 0064.

Относительная погрешность приблизительно равна 1,5%. Она значительно больше, чем начальный член ее разложения, но имеет то же знак. Поскольку ε = 4/5 = 0,8, не слишком мало наше замечание годится для всей картины и ведет к увеличению нашей веры в предположение.

Приближенные формулы играют в прикладной математике важную роль. пытаясь оценить такую формулы, мы часто на практике применяем процедуру, которой следовали в этом параграфе. Мы вычисляем начальный член разложения относительной погрешности и дополняем полученную таким путем информацию численными проверками, рассмотрениями по аналогии и т. д., короче, индуктивными, недоказательными рассуждениями.

3. Пределы. Для того чтобы увидеть индуктивное рассуждение в действии еще и в другой области, рассмотрим следующую задачу[28].

Пусть a₁, a₂, …, a_n — произвольная последовательность положительных чисел. Показать, что

Эта задача требует некоторых предварительных знаний, особенно знакомства с понятием «lim sup», или «верхнего предела последовательности»[29]. Однако, если даже вы полностью знакомы с этим понятием, вы можете испытать некоторые трудности в нахождении доказательства. Я приношу свои поздравления любому студенту, который сможет в несколько часов без посторонней помощи решить эту задачу.

Если вы сами хоть немного побились над этой задачей, то вы сможете с бо́льшим участием переживать борьбу, описанную в следующих параграфах.

4. Попытка опровергнуть. Начинаем с обычных вопросов.

В чем состоит посылка?[31] Только в том, что a_n > 0, ни в чем другом.

102

В чем состоит заключение? В этом неравенстве с e в правой части и сложным пределом в левой.

Известна ли вам какая-нибудь родственная теорема? Нет, пожалуй. Это очень непохоже на все, что я знаю.

Вероятно ли, что теорема верна? Или более вероятно, что она неверна? Конечно неверна. В самом деле я не могу поверить, что из такой широкой посылки, всего лишь из того, что a_n > 0, может быть выведено такое точное следствие.

Что вам требуется сделать? Доказать теорему. Или опровергнуть ее. Я очень стою за опровержение.

Можете ли вы проверить какой-нибудь частный случай теоремы? Да, это то, что я собираюсь сделать.

[Для того чтобы упростить формулы, положим

Пробую a_n = 1 для n = 1, 2¸ 3, … Тогда

В этом случае заключение теоремы подтверждается.

Однако я мог бы положить a₁ = 0, a_n = 1 для n = 2¸ 3, 4 … Тогда

Теорема опровергнута,[32] Нет, это не так. Посылка разрешает a₁ = 0,00001, но запрещает a₁ = 0. Вот жалость!

Попробую что-нибудь другое. Пусть a_n = n. Тогда

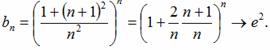
Снова подтвердилось.

Пусть теперь a_n = n². Тогда

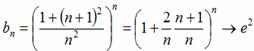
Снова подтвердилось. И снова e². Нельзя ли в правой части заключения вместо e поставить e²? Это усилило бы теорему.

Введу параметр. Возьму … Да, возьму a₁ = c, где c я оставлю в своем распоряжении, но a_n = n для n = 2, 3, 4, … Тогда

103

e^{1 + c} всегда > e, так как c = a₁ > 0. Однако e^{1 + c} может быть сколь угодно близким к e, потому что c может быть, произвольно мало. Я не могу опровергнуть, я не могу доказать.

Еще только одно испытание. Возьму a_n = n^c. Тогда [мы опускаем некоторые выкладки]

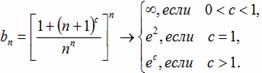
Снова предел может сколь угодно близко подходить к e, но всегда остается больше e. Мне никак не удается опустить этот … предел ниже e. Пришло время изменить точку зрения.

5. Попытка доказать. В самом деле, основания для изменения точки зрения очень сильны. В свете накопленных индивидуальных доводов перспектива опровергнуть теорему кажется столь тусклой, что перспектива ее доказательства выглядит относительно яркой.

Поэтому ничего не остается кроме как приступить к новому исследованию теоремы, ее формулировки, ее посылки, ее заключения, связанных с нею понятий и т. д.

Можете ли вы ослабить посылку? Нет, не могу. Если я допускаю a_n = 0, то заключение перестает быть справедливым, теорема становится неверной (a₁ = 0, a₂ = a₃ = a₄ = … = 1).

Можете ли вы усилить заключение? Я, безусловно, не могу его усилить, подставив вместо e какое-нибудь большое число, так как в этом случае заключение перестает быть справедливым, теорема становится неверной (примеры в предыдущем § 4).

Принимали ли вы в расчет все существенные понятия, связанные с задачей? Нет, не принимал. Быть может, отсюда и затруднения.

Что вы не приняли в расчет? Определение lim sup. Определение числа e.

Что такое lim sup b_n? Это верхний предел последовательности b_n при n → ∞.

Что такое e? Я могу определить e различными способами. Приведенные выше примеры наводят на мысль, что обычное определение e может оказаться наилучшим:

Могли бы вы иначе сформулировать теорему?..

Могли бы вы сформулировать теорему в какой-нибудь более доступной форме?..

Могли бы вы иначе сформулировать заключение? В чем состоит заключение? Заключение содержит e. Что такое e? (Я уже задавал этот вопрос раньше[33].)

104

О, да — вот заключение:

или, что то же самое,

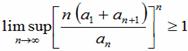
Это выглядит значительно лучше!

Может ли заключение быть неверным, когда выполнена посылка? Да, это и есть наш вопрос. Подумаю об этом. Рассмотрю отрицание утверждения, в точности противоположное утверждение. Запишу его:

(?)

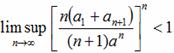Я ставлю рядом с ним знак вопроса, потому что именно этот пункт подвергается сомнению. Назову его «формулой (?)». что формула (?) означает? Конечно, она означает, что существует такое N, что

Отсюда следует, что

Далее следует… Попробую что-нибудь. Да, я могу записать это очень стройно! Из (?) далее следует, что

или

Выпишу это подробнее. Отсюда следует, что

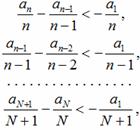
и, таким образом,

105

где C — постоянная, не зависящая от n, если только n ≥ N. Это совсем не важно, но на самом деле

Важно, однако, что n может быть произвольно велико и что гармонический ряд расходится. Поэтому отсюда следует, что

Но это решительно противоречит предположению, что a_n > 0 для n = 1, 2, 3, … Тем не менее это противоречие безукоризненно следует из формулы (?). поэтому, действительно, источником противоречия является формула (?); формула (?) несовместима с посылкой a_n > 0; противоположное утверждение к (?) должно быть верно — теорема доказана!

6. Роль индуктивной фазы. Поверхностно просматривая предыдущее доказательство, мы могли бы подумать, что первая, индуктивная фаза решения (§ 4) вообще не применяется во второй, доказательной фазе (§ 5). Однако это не так. Индуктивная фаза была полезна в нескольких отношениях.

Во-первых, исследуя конкретные частные случаи теоремы, мы до конца ее поняли и осознали ее полное значение. Мы убедились, что ее посылка существенна, ее заключение точно. Это знание было полезно во второй фазе: мы знали, что должны воспользоваться всей посылкой и принять в расчет точное значение постоянной.

Во-вторых, убедившись в том, что теорема верна в нескольких частных случаях, мы приобрели сильные индуктивные доводы в ее пользу. Индуктивная фаза преодолела наше первоначальное сомнение и дала нам сильную уверенность в теореме. Без такой уверенности мы едва ли нашли бы мужество предпринять доказательство, которое вовсе не выглядело привычным делом. «Когда вы убедитесь, что теорема верна, вы начинаете ее доказывать» — традиционный профессор математики совершенно прав.

В третьих, примеры, в которых известная предельная формула для e выскакивала всё снова и снова, дали нам разумное основание для введения этой предельной формулы и в формулировку теоремы. А это введение оказалось решающим шагом на пути к решению.

В целом кажется естественным и разумным, что индуктивная фаза предшествует доказательной фазе. Сначала догадайтесь, потом докажите.

106

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ V

1. Перемножая ряды

вы найдете первые члены разложения

(a) Вычислите еще несколько членов и попытайтесь догадаться, каков общий член.

(b) Покажите, что y удовлетворяет дифференциальному уравнению

(1 — x²) y′ — xy = 1,

и воспользуйтесь этим уравнением, чтобы доказать вашу догадку.

2. Перемножая ряды

вы найдете первые члены разложения

(a) Вычислите еще несколько членов и попытайтесь догадаться, каков общий член.

(b) Выша догадка, если она правильна, наводит на мысль, что y удовлетворяет простому дифференциальному уравнению. Установив это уравнение, докажите вашу догадку.

3. Функциональное уравнение

удовлетворяется степенным рядом

Проверьте эти коэффициенты, определите, если необходимо, еще несколько и попытайтесь догадаться, каков общий член.

4. Функциональное уравнение

удовлетворяется степенным рядом

f(x) = 1 + x + x² + 2x³ + 4x⁴ + … + a_nxⁿ +…

107

Утверждается, что a_n есть число структурно различных химических соединений (алифатических алкоголей)¸ имеющих одну и ту же химическую формулу C_nH_2n+1OH. В случае n = 4 ответ верен. Существует a₄ = 4 алкоголей C₄H₉OH; они представлены на рис 5.1, каждое соединение изображено в виде «дерева», каждая C — в виде маленького кружка или «узла» и радикал OH — в виде стрелки; H опускается[30]. Проверьте другие значения n.

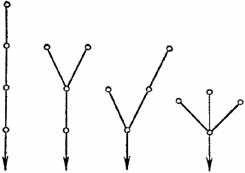
Рис. 5.1. Соединения C₄H₉OH

5.

v

6. Эллипс описывает вытянутый или сплющенный сфероид в зависимости от того, вращается ли он вокруг большой или малой оси.

7. Для площади вытянутого сфероида

E = 2πab [(1 — ε²)^½ + (arcsin ε)/ε], P = 4π (a² + 2b²)/3

соответственно — точное и приближенное выражения. Найдите

(a) начальный член относительной погрешности,

(b) относительную погрешность, когда b = 0.

Что можно сказать о знаке относительной погрешности?

8. Сравнивая примеры 6 и 7, какую приближенную формулу предложили бы вы для площади поверхности трехосного эллипсоида с полуосями a, b и c?

Что можно сказать о знаке относительной погрешности?

9. [§ 2]. Исходя из параметрического представления эллипса, x = a sin t, y = b cos t, покажите, что

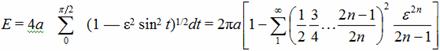
и выведите отсюда начальные члены, приведенные без доказательства в § 2.

10 (продолжение). Пользуясь разложением по степеням ε, докажите, что E > P для 0 < ε ≤ 1.

108

11 [§ 2]. Определите число α так, чтобы выражение

P″ = πP + (1 — α) P′

Давало наилучшее возможное приближение E для малого ε. (Т. е. порядок начального члена разложения погрешности (P″ — E)/E должен быть настолько высоким, насколько это возможно.)

12 (продолжение). Исследуйте приближение посредством Pⁿ, следуя методу § 2. (Индуктивно!)

13. Пусть дано положительное целое число p и последовательность положительных чисел a₁, a₂, a₂, …, a_n, … Покажите, что

14 (продолжение). Укажите последовательность a₁, a₂, a₃, …, для которой достигается равенство.

15. Объясните наблюдаемые закономерности. Открытие в физике часто достигается в два шага. Сначала в данных наблюдений подмечается некоторая закономерность. Затем эта закономерность объясняется как следствие какого-либо общего закона. Эти два шага могут быть отделены большим промежутком времени, и их могут делать разные люди. Великий пример Кеплера и Ньютона: закономерности в движении планет, наблюдавшиеся Кеплером, были объяснены законом тяготения, открытым Ньютоном. Нечто подобное может случиться в математическом исследовании, и вот изящный пример, требующий небольших предварительных знаний.

Обычная таблица четырехзначных десятичных логарифмов содержит 900 мантисс, а именно мантиссы целых чисел от 100 до 999. до наблюдения мы, возможно, склонны думать, что десять цифр 0, 1, …, 9 встречаются в этих таблицах приблизительно одинаково часто, но это не так: в качестве первой цифры мантиссы они, несомненно, появляются не одинаково часто. Сосчитав мантиссы, имеющие одни и те же первые цифры, получим табл. I (проверьте ее!).

Таблица I. Мантиссы с одной и той же первой цифрой в четырехзначных логарифмах

Первая цифра	Число мантисс	Отношения
0 1 2 3 4 5 6 7 8 9	26 33 41 52 65 82 103 129 164 205	1,269 1,242 1,268 1,250 1,262 1,256 1,252 1,271 1,250
	Всего 900

Рассматривая второй столбец табл. I, мы можем заметить, что в нем любые два последовательных числа имеют приблизительно одинаковое отношение. Это побуждает нас вычислить эти отношения с несколькими десятичными знаками: они записаны в последнем столбце таблицы.

109

Почему эти отношения приблизительно равны? Попытайтесь за наблюдаемой приближенной закономерностью разглядеть какую-нибудь точную закономерность. Числа во втором столбце табл. I приблизительно являются членами геометрической прогрессии. Можете ли вы открыть точную геометрическую прогрессию, с которой просто связаны члены приближенной прогрессии? [Знаменатель точной прогрессии, возможно, должен быть какого-то рода средним отношений, записанных в последнем столбце табл. I.]

Рис. 5.2. Симметрия фризов.

16. Классифицируйте наблюдаемые факты. Значительная часть работы натуралиста посвящена описанию и классификации объектов, которые он наблюдает. Такая работа была преобладающей в течение долгого времени после Линнея, когда главная деятельность натуралистов состояла в описании новых видов и родов растений и животных и в переклассификации известных видов и родов. Натуралисты описывают и классифицируют не только растения и животных, но и другие объекты, особенно минералы; классификация кристаллов основана на их симметрии. Хорошая классификация важна; она сводит разнообразие объектов наблюдения к относительно небольшому числу ясно характеризуемых и хорошо упорядоченных типов. Математик не часто имеет возможность позволить себе удовольствие описания и классификации, но это может случиться.

Если вы знакомы с несколькими понятиями плоской геометрии (ось симметрии, центр симметрии), то вы можете позабавиться узорами. Рис. 5.2. показывает четырнадцать узорных полос, каждая из которых

110

порождается простой фигурой, периодически повторяемой вдоль (горизонтальной) прямой. Назовем такую полосу «фризом». Подберите для каждого фриза на левой стороне (помеченного числом) фриз на правой стороне (помеченный буквой) так, чтобы два подобранных фриза имели один и тот же тип симметрии. Кроме того, исследуйте узорные полосы, которые вы можете найти на всех видах объектов или в старых архитектурных работах, и попытайтесь подобрать для каждой фриз на рис. 5.2. Наконец, дайте полный список различных типов симметрии, которые могут иметь фризы, и исчерпывающее описание каждого типа симметрии. [Рассматривайте фриз как бесконечно длинный в обоих направлениях, а порождающую фигуру как периодически повторяющуюся бесконечное число раз. Заметьте, что термин «тип симметрии» не был формально определен. Прийти к подходящей интерпретации этого термина — важная часть вашей задачи.]

17. Найдите на рис 5.3 два узора, имеющие один и тот же тип симметрии. Каждый узор следует себе представлять как покрывающий всю плоскость своими повторяющимися кусками.

Рис. 5.3. Симметрия обоев.

18. В чем различие? Двадцать шесть заглавных букв латинского алфавита следующим образом подразделены на пять групп:

A M N U V W Y

B C C E K

N S Z

H I O X

F G J L P Q R

Чем они отличаются? Каково могло бы быть простое основание для предлагаемой классификации [Посмотрите на пять уравнений:

y = x², y² = x, y = x³, x² + 2 y² = 1, y = x + x⁴.

Чем они отличаются?]

VI. ОДНО БОЛЕЕ ОБЩЕЕ УТВЕРЖДЕНИЕ

Он [Эйлер] предпочитал обучение своих учеников тому небольшому удовлетворению, которое он получил бы, изумляя их. он думал, что недостаточно сделал бы для науки, если бы не прибавил к открытиям, которыми он обогатил науку, чистосердечного изложения идей, приведших его к этим открытиям. — Кондорсэ

1. Эйлер. Из всех математиков, с работами которых я сколько-нибудь знаком, Эйлер, по-видимому, для рассматриваемого нами вопроса является наиболее важным. Мастер индуктивного исследования в математике, он сделал важные открытия (о бесконечных рядах, в теории чисел и в других областях математики) с помощью индукции, т. е. с помощью наблюдения, дерзкой догадки и проницательных подтверждений. Однако Эйлер в этом отношении не является единственным; другие математики, большие и малые, в своей работе широко пользуются индукцией.

Все же в одном отношении Эйлер кажется мне почти единственным: он старается изложить относящиеся к вопросу индуктивные доводы заботливо, в деталях, в хорошем порядке. Он излагает их убедительно, но честно, как это подобает настоящему ученому. Его изложение является «чистосердечным изложением идей, приведших его к этим открытиям» и имеет особую прелесть. Вполне естественно, что, как и любой другой автор, он пытается убедить своих читателей, но как действительно хороший автор, он пытается убедить их только тем, в чем по-настоящему убежден сам.

Следующий параграф дает пример того, как писал Эйлер. Выбранный мемуар требует лишь небольших предварительных знаний и целиком посвящен изложению индуктивного рассуждения.

2. Мемуар Эйлера приведен здесь в переводе in extenso[31], если исключить небольшое число несущественных изменений, которые должны сделать его более доступным современному читателю[32]

112

ОТКРЫТИЕ НАИБОЛЕЕ НЕОБЫЧАЙНОГО ЗАКОНА ЧИСЕЛ, ОТНОСЯЩЕГОСЯ К СУММАМ ИХ ДЕЛИТЕЛЕЙ

1. До сих пор математики тщетно пытались обнаружить в последовательности простых чисел какой-либо порядок, и мы имеем все основания верить, что здесь существует какая-то тайна, в которую человеческий ум никогда не проникнет. Чтобы убедиться, следует только взглянуть на таблицу простых чисел, которую некоторые взяли на себя труд вычислить дальше, чем до ста тысяч, и осознать, что здесь нет никакого порядка и никакого правила. Это тем более удивительно, что арифметика дает нам определенные правила, с помощью которых мы можем продолжать последовательность простых чисел сколь угодно далеко, не замечая, однако, ни малейшего следа порядка. Я сам, конечно, далек от этой цели. Но мне удалось открыть чрезвычайно странный закон, управляющий последовательностью сумм делителей целых чисел, которая на первый взгляд кажется неправильной ровно в той же степени, как и последовательность простых чисел, и которая в некотором смысле даже включает в себя эту последнюю. Этот закон, который я вскоре объясню, по моему мнению, тем более замечателен, что он имеет такую природу, что мы можем быть уверены в его справедливости, не давая ему безукоризненного доказательства. Тем не менее я представлю в его пользу такие доводы, которые можно рассматривать как почти равносильные строгому доказательству.

2. Простое число не имеет делителей, за исключением единицы и самого себя, и это отличает простые числа от других чисел. Там[34] 7 есть простое число, потому что оно делится только на 1 и на себя. Любое другое число, имеющее кроме единицы и самого себя другие делители, называется составным, как, например, число 15, которое кроме 1 и 14 имеет делители 3 и 5. Следовательно, вообще, если число p простое, оно будет делиться только на 1 и p; но если бы p было составным, то оно имело бы кроме 1 и p другие делители. Поэтому в первом случае сумма его делителей будет равна 1 + p, но во втором она превышает 1 + p. Поскольку я собираюсь рассматривать суммы делителей различных чисел, для обозначения суммы делителей числа n я буду пользоваться[33] символом σ (n). Так, σ (12) обозначает сумму всех делителей числа 12, каковыми являются 1, 2, 3, 4, 6 и 12, следовательно, σ (12) = 28. Таким же образом можно видеть, что σ (60) = 168 и σ (100) = 217. Однако, так как единится делится только на себя, σ (1) = 1. далее, 0 (нуль) делится на все числа. Поэтому σ (0) должно было бы, собственно, быть бесконечного. (Однако я буду приписывать ему позднее конечные значения, различные в различных случаях, и это окажется полезным.)

113

3. Определив, как выше, значение символа σ (n), мы ясно видим, что если p простое число, то σ (p) = 1+ p. Вместе с тем σ (1) = 1 (а не 1 + 1); отсюда мы видим, что из последовательности простых чисел 1 должна быть исключена; 1 есть начальное целое число, ни простое, ни составное. Если, однако, n составное, то σ (n) больше, чем 1+ n.

В этом случае мы легко можем найти σ (n) по множителям n. Если a, b, c, d … — различные простые числа, то легко видим, что

σ (ab) = 1 + a + b + ab = (1 + a)(1 +b) = σ (a) σ (b),

σ (abc) = (1 + a)(1 +b) )(1 +c) = σ (a) σ (b) σ (c),

σ (abcd) = σ (a) σ (b) σ (c) σ (d)

и так далее. Нам нужны специальные правила для степеней простых чисел, как

и вообще

Пользуясь этим, мы можем найти сумму делителей любого числа, составленного каким бы то ни было способом. Это мы видим из формул

σ(a²b) = σ(a²) σ(b)

σ(a³b²) = σ(a³) σ(b²)

σ(a³b⁴c) = σ(a³) σ(b⁴) σ(c)

и вообще

σ(a^αb^βc^γd^δe^ε) = σ(a^α) σ(b^β) σ(c^γ) σ(d^δ) σ(e^ε)

Например, чтобы найти σ(360), полагаем, так как 360 разлагается на множители 2³·3²·5:

σ(360) = σ(2³) σ(3²) σ(5) = 1170.

4. Чтобы показать последовательность сумм делителей, я привожу следующую таблицу[34], содержащую суммы делителей всех целых чисел от 1 до 99.

114

N	0	1	2	3	4	5	6	7	8	9
0	—	1	3	4	7	6	12	8	15	13
10	18	12	28	14	24	24	31	18	39	20
20	42	32	63	48	54	48	91	38	60	56
30	72	32	63	48	64	48	91	38	60	56
40	90	42	96	44	84	78	72	48	124	57
50	93	72	98	54	120	72	120	80	90	60
60	168	62	96	104	127	84	144	68	126	96
70	144	72	195	74	114	124	140	96	168	80
80	186	121	126	84	224	108	132	120	180	90
90	234	112	168	128	144	120	252	98	171	156

Посмотрев немного на последовательность этих чисел, мы едва ли не придем в отчаяние. Нет надежды обнаружить хоть малейший порядок. Неправильность простых чисел так глубоко вплетена в нее, что мы должны считать невозможным распутать некий закон, управляющий этой последовательностью, если мы не знаем закона, управляющего последовательностью самых простых чисел. Могло бы даже показаться, что последовательность, находящаяся перед нами, еще более таинственна, чем последовательность простых чисел.

5. Тем не менее я заметил, что эта последовательность подчиняется вполне определенному закону и может даже рассматриваться как рекуррентная последовательность. Это математическое выражение означает, что каждый член может быть по неизменному правилу вычислен по предыдущим членам. Действительно, если σ (n) означает любой член этой последовательности, а σ (n — 1), σ (n — 2), σ (n — 3), σ (n — 4), σ (n — 5),… — предшествующие члены, то я утверждаю, что значение σ (n) всегда можно получить по нескольким предыдущим, как предписывается следующей формулой:

σ (n) = σ (n — 1) + σ (n — 2) — ), σ (n — 5) — ), σ (n — 7) + σ (n — 12) + σ (n — 15) — σ (n — 22) — σ (n — 26) +

+ σ (n — 35) + σ (n — 40) — σ (n — 51) — σ (n — 57) + σ (n — 70) + σ (n — 77) — σ (n — 92) — σ (n — 100) + ….

К этой формуле мы должны сделать следующие замечания:

I. Знаки + и — в правой части формулы попарно чередуются.

II. Закон чисел 1, 2, 5, 7, 12, 15, …, которые мы должны вычитать из рассматриваемого числа n, станет ясен, если мы возьмем их разности.

Числа 1, 2, 5, 7, 12, 15, 22, 26, 35, 40, 51, 57, 70, 77, 92, 100, …

Разности 1, 3, 2, 5, 3, 7, 4, 9, 5, 11, 6, 13, 7, 15, 8, …

В самом деле, мы имеем здесь поочередно все целые числа 1, 2, 3, 4,

115

5, 6, … и нечетные числа 3, 5, 7, 9, 11, …, и поэтому мы можем продолжать последовательность этих чисел сколь угодно далеко.

III. Хотя эта последовательность бесконечна, мы должны в каждом случае брать только те члены, для которых числа, стоящие под знаком σ, еще положительны, и опускать σ для отрицательных значений.

IV. Если в нашей формуле встретится символ σ(0), то, поскольку его значение само по себе является неопределенным, мы должны подставить вместо σ(0) рассматриваемое число n.

6. После этих замечаний нетрудно применить формулу к любому данному частному случаю, и таким образом всякий может убедиться в ее справедливости на стольких примерах, сколько он пожелает разобрать. И так как я должен признать, что не в состоянии дать ей строгое доказательство, я оправдаю ее достаточно большим числом примеров.

σ(1) = σ(0)	= 1	= 1
σ(2) = σ(1) + σ(0)	= 1 + 2	= 3
σ(3) = σ(2) + σ(1)	= 3 + 1	= 4
σ(4) = σ(3) + σ(2)	= 4 + 3	= 7
σ(5) = σ(4) + σ(3) — σ(0)	= 7 +4 — 5	= 6
σ(6) = σ(5) + σ(4) — σ(1)	= 6 +7 —1	= 12
σ(7) = σ(6) + σ(5) — σ(2) — σ(0)	= 12 + 6 — 3 — 7	= 8
σ(8) = σ(7) + σ(6) — σ(3) — σ(1)	= 8 + 12 — 4 — 1	= 15
σ(9) = σ(8) + σ(7) — σ(4) — σ(2)	= 15 + 8 — 7 — 3	= 13
σ(10) = σ(9) + σ(8) — σ(5) — σ(3)	= 13 + 15 — 6 — 4	= 18
σ(11) = σ(10) + σ(9) — σ(6) — σ(4)	= 18 + 13 — 12 — 7	= 12
σ(12) = σ(11) + σ(10) — σ(7) — σ(5) + σ(0)	= 12 + 18 — 8 — 6 + 12	= 28
σ(13) = σ(12) + σ(11) — σ(8) — σ(6) + σ(1)	= 28 + 12 — 15 — 12 + 1	= 14
σ(14) = σ(13) + σ(12) — σ(9) — σ(7) + σ(2)	= 14 + 28 — 13 — 8 + 3	= 24
σ(15) = σ(14) + σ(13) — σ(10) — σ(8) + σ(3) + σ(0)	= 24 + 14 — 18 — 15 + 4 + 15	= 24
σ(16) = σ(15) + σ(14) — σ(11) — σ(9) + σ(4) + σ(1)	= 24 + 24 — 12 — 13 + 7 + 1	= 31
σ(17) = σ(16) + σ(15) — σ(12) — σ(10) + σ(5) + σ(2)	= 31 + 24 — 28 — 18 + 6 + 3	= 18
σ(18) = σ(17) + σ(16) — σ(13) — σ(11) + σ(6) + σ(3)	= 18 + 31 — 14 — 12 + 12 + 4	= 39
σ(19) = σ(18) + σ(17) — σ(14) — σ(12) + σ(7) + σ(4)	= 39 + 18 — 24 — 28 + 8 + 7	= 20
σ(20) = σ(19) + σ(18) — σ(15) — σ(13) + σ(8) + σ(5)	= 20 + 39 — 24 — 14 + 15 + 6	= 42

Я думаю, этих примеров достаточно, чтобы заставить любого отказаться от представления, что мое правило находится в согласии с истиной лишь по простой случайности.

7. Однако, так как в рассмотренных примера участвуют только первые шесть из чисел 1, 2, 5, 7, 12, 15, 22, …, которые мы должны вычитать, кто-нибудь мог бы еще сомневаться, будет ли закон для этих чисел точно таким, как я указал. Таким образом, этот закон мог бы еще показаться недостаточно установленным, и поэтому я приведу несколько примеров с бо́льшими числами.

116

I. Дано число 101; найти сумму его делителей. Имеем

σ(101) = σ(100) + σ(99) — σ(96) — σ(94) + σ(89) + σ(86) — σ(79) — σ(75) +

+ σ(66) + σ(61) — σ(50) — σ(44) + σ(31) + σ(24) — σ(9) — σ(1) =

= 217 + 156 —252 — 144 +90 + 132 — 80 —124 + 144 + 62 — 93 — 84 + 32 + 60 — 13 — 1 =

= 893 — 791 = 102

и отсюда мы могли бы заключить, если бы это не было известно раньше, что 101 есть простое число.

II. Дано число 301; найти сумму его делителей. Имеем

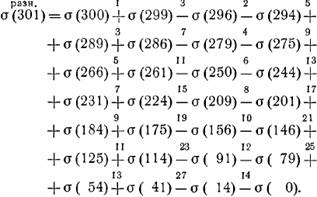
На этом примере видно, как мы можем, пользуясь разностями, продолжать формулу, насколько это необходимо в каждом случае. Производя вычисления, находим

σ(301) = 4939 — 4587 — 352

Отсюда мы видим, что 301 не является простым числом. Действительно, 301 — 7·43, и мы получаем

σ(301) = σ(7) σ(43) = 8·44 = 352,

как и показало наше правило.

8 Примеры, которые я только что разобрал, безусловно рассеют любые сомнения, которые мы могли бы иметь в отношении справедливости моей формулы. Это прекрасное свойство чисел тем более удивительно, что мы не чувствуем никакой разумной связи между структурой моей формулы и природой делителей, с сумой которых мы имеем здесь дело. Последовательность чисел 1, 2, 5, 7, 12,

117

12, …, казалось бы, не имеет к рассматриваемому вопросу никакого отношения. Более того, поскольку закон этих чисел «прерывист» и они фактически являются смесью двух последовательностей с правильным законом: 1, 5, 12, 22, 35, 51,… и 2, 7, 15, 26, 40, 57, …, мы не могли ожидать, что такая неправильность может встретиться в Анализе. Отсутствие доказательства должно вызвать еще большее удивление, так как кажется совершенно невозможным, чтобы такое свойство удалось открыть, не руководствуясь каким-либо надежным методом, который мог бы заменить безукоризненное доказательство. Я признаюсь, что не чисто случайно наткнулся на это открытие, но что другое предложение проложило путь к этому прекрасному свойству — другое предложение той же природы, которое должно быть принято как верное, хотя я не в состоянии его доказать. И хотя мы здесь рассматриваем природу целых чисел, к которой Исчисление Бесконечно Малых кажется неприложимым, тем не менее я пришел к своему заключение[35] с помощью дифференцирований и других уловок. Я желал бы, чтобы кто-нибудь другой нашел более короткий и более естественный путь, и, быть может, рассмотрение того пути, которому я следовал, могло бы оказать здесь некоторую помощь.

9. Рассматривая разбиения чисел, я много лет тому назад исследовал выражение

(1 — x) (1 — x²) (1 — x³) (1 — x⁴) (1 — x⁵) (1 — x⁶) (1 — x⁷) (1 — x⁸)…,

где произведение предполагается бесконечным. Чтобы увидеть, какого рода ряд получится в результате, я фактически перемножил большое число множителей и нашел

1 — x — x² + x⁵ + x⁷ — x¹² — x¹⁵ + x²² + x²⁶— x³⁵ — x⁴⁰ +…

Последовательность показателей степени x совпадает с последовательностью чисел, входящей в приведенную выше формулу; знаки + и — попарно чередуются. Достаточно предпринять это перемножение и продолжить его сколь угодно далеко, чтобы убедиться в том, что этот ряд верен. Однако у меня нет для этого никаких других доводов за исключением длинной индукции, которую я провел так далеко, что никоим образом не могу сомневаться в законе, управляющем образованием этих членов и их степеней. Я долго тщетно разыскивал строгое доказательство равенства между этим рядом и написанным выше бесконечным произведением (1 — x) (1 — x²) × (1 — x³)…, и я предложил этот же вопрос некоторым из моих друзей, способности которых в этом отношении мне известны, но все согласились со мной, что это преобразование произведения в ряд верно, хотя никто не сумел раскопать какой-нибудь ключ для доказательства. Таким образом, это познанная, но все же не доказанная истина, что если мы положим

s = (1 — x) (1 — x²) (1 — x³) (1 — x⁴) (1 — x⁵) (1 — x⁶)…,

118

то эта же величина s может быть выражена и следующим образом:

s = 1 — x — x² + x⁵ + x⁷ — x¹² — x¹⁵ + x²² + x²⁶— x³⁵ — x⁴⁰ +…

Ибо каждый из нас может в этой истине убедиться, производя перемножение сколь угодно большого числа множителей, и кажется невозможным, чтобы закон, который, как было обнаружено, выполняется, например, для 20 членов, нельзя было бы наблюдать и для следующих членов.

10. Поскольку мы таким образом обнаружили, что эти два бесконечных выражения равны, хоти и оказалось невозможным это доказать, все заключения, которые могут быть из этого выведены, будут той же природы, т. е. будут верны, но не доказаны. Или если бы одно из этих заключений можно было доказать, то, наоборот, можно было бы получить ключ к доказательству этого равенства; и именно с таким намерением я различными способами манипулировал этими двумя выражениями и, таким путем, среди других открытий пришел к тому, которое я объяснил выше; его справедливость должна быть поэтому столь же несомненной, как и справедливость равенства между этими двумя бесконечными выражениями. Я поступил следующим образом. Пусть дано, что два выражения

I. s = (1 — x) (1 — x²) (1 — x³) (1 — x⁴) (1 — x⁵) (1 — x⁶) (1 — x⁷) (1 — x⁸)…,

II. s =1 — x — x² + x⁵ + x⁷ — x¹² — x¹⁵ + x²² + x²⁶— x³⁵ — x⁴⁰ +…

равны. Я избавился от множителей в первом, взяв логарифмы:

ln s = ln (1 — x) + ln (1 — x²) + ln (1 — x³) + ln (1 — x⁴) +…

Чтобы избавиться от логарифмов, я дифференцирую и получаю равенство

или

Из второго выражения для s в виде бесконечного ряда получаем другое значение той же самой величины:

11. Положим

119

Мы имеем выше два выражения для величины t. В первом выражении я разлагаю каждый член в геометрическую прогрессию и получаю

t = x +	x^2	+ x^3	+ x^4	+ x^5	+ x^6	+ x^7	+ x^8	+…
+	2x^2		+ 2x^4		+ 2x^6		+ 2x^8	+…
		+ 3x^3			+ 3x^6			+…
			+ 4x^4				+ 4x^8	+…
				+ 5x^5				+…
					+ 6x^6			+…
						+ 7x^7		+…
							+ 8x^8	+…

Мы легко здесь находим, что каждая степень x встречается столько раз, сколько ее показатель имеет делителей, и что каждый делитель появляется в качестве коэффициента при той же самой степени x. Следовательно, если мы соберем члены с одинаковыми степенями, то коэффициенты при каждой степени x будут суммой делителей показателей степени. И, следовательно, пользуясь введенным выше обозначением σ (n) для суммы делителей числа n, я получаю

t = σ(1)x + σ(2)x² + σ(3)x³ + σ(4)x⁴ + σ(5)x⁵ +…

Закон ряда очевиден. И хотя может показаться, что в определении коэффициентов участвовала индукция, мы легко можем убедиться, что этот закон является неизбежным следствием.

12. В силу определения t последняя формула п. 10 может быть записана следующим образом:

t(1 — x — x² + x⁵ + x⁷ — x¹² — x¹⁵ + x²² + x²⁶ —…) —

— 1 — x — 2x² + 5x⁵ + 7x⁷ — 12x¹² — 15x¹⁵ + 22x²² + 26x²⁶ —… = 0.

Подставляя вместо t значение, полученное в конце п. 11, находим

0 =	σ(1)x +	σ(2)x^2+	σ(3)x^3+	σ(4)x^4+	σ(5)x^5+	σ(6)x^6+ …
	— x —	σ(1)x^2—	σ(2)x^3—	σ(3)x^4—	σ(4)x^5—	σ(5)x^6— …
		— 2 x^2—	σ(1)x^3—	σ(2)x^4—	σ(3)x^5—	σ(4)x^6— …
					+ σ(5)x^5+	σ(1)x^6— …

Приводя подобные члены, находим коэффициент при любой данной степени x, а затем суммы делителей некоторых меньших чисел, полученных из этого показателя степени вычитанием последовательно 1, 2, 5, 7, 12, 15, 22, 26, … Наконец, если показатель степени принадлежит к этой последовательности, то появляется он сам. Нет необходимости еще раз

120

объяснять знаки, приписываемые только что перечисленным членам. Следовательно, вообще коэффициентом при xⁿ будет

σ(n) — σ(n — 1) — σ(n — 2) + σ(n — 5) + σ(n — 7) — σ(n — 12) — σ(n — 15) +…

Это продолжается до того момента, пока числа под знаком σ остаются неотрицательными. Однако если появляется член σ(0), мы должны подставить вместо него n.

13. Так как сумма бесконечного ряда, рассмотренного в предыдущем п. 12, равна 0, то каково бы ни было значение x, коэффициент при каждой отдельной степени x обязательно должен быть равен 0. Отсюда мы получаем закон, который я объяснил выше в п. 5; я имею в виду закон, управляющий суммами делителей и дающий нам возможность рекуррентно их вычислять для всех чисел. В предыдущем выводе мы можем уловить некоторое основание для знаков, некоторое основание для последовательности чисел

1, 2, 5, 7, 12, 22, 26, 35, 40, 51, 57, 70, 77, …,

и особенно основание для того, почему вместо σ(0) мы должны подставлять само число n, что могло показаться наиболее странным свойством моего правила. Это рассуждение, хотя и все еще очень далекое от полного доказательства, безусловно не оставит никаких сомнений относительно необычайного закона, который я здесь объяснил.

3. Переход к более общей точке зрения. Приведенный текст Эйлера необычайно поучителен. Мы можем из него почерпнуть много важных сведений о математике или о психологии изобретения или об индуктивных рассуждениях. Примеры и примечания в конце этой главы дают возможность исследовать некоторые из математических идей Эйлера, но теперь мы хотим сосредоточить свое внимание на его индуктивном рассуждении.

Теорема, исследованная Эйлером, замечательна в нескольких отношениях и даже сегодня имеет большой математический интерес. Однако нас здесь интересует не столько математическое содержание этой теоремы, сколько доводы, заставившие Эйлера поверить в теорему, когда она все еще не была доказана. Чтобы лучше понять природу этих доводов, я не буду обращать внимания на математическое содержание мемуара Эйлера и дам только схематический очерк, делая ударение на некотором общем аспекте его индуктивного рассуждения.

Поскольку мы будем пренебрегать математическим содержанием различных теорем, которые мы должны рассмотреть, нам будет выгодно обозначить их буквами T, T^*, C₁, C₂, …, C^*₁, C^*₂, … Читатель может совершенно игнорировать значение этих букв. Но, если бы он пожелал отыскать их в тексте Эйлера, вот ключ:

121

T есть теорема

(1 — x) (1 — x²) (1 — x³)… = 1 — x — x² + x⁵ + x⁷— x¹² — x¹⁵ +…

Закон чисел 1, 2, 5, 7, 12, 15, … объяснен в § 2, п. 5, II.

C_n есть утверждение, что коэффициенты при xⁿ в обеих частях предыдущего равенства одинаковы. Например, C₆ утверждает, что, разлагая произведение в левой части равенства, мы найдем, что коэффициент при x⁶ равен 0. заметьте, что C_n есть следствие теоремы T.

C^*_n есть равенство

σ (n) = σ (n — 1) + σ (n — 2) — σ (n — 5) — ), σ (n — 7) +…,

подробно объясненное в § 2, п. 5. Например, C^*₆ утверждает, что

σ (6) = σ (5) + σ (4) — σ (1).

T^* есть «наиболее необычный закон», утверждающий, что все C^*₁, C^*₂, C^*₃, … верны. Заметьте, что C^*_n есть следствие (частный случай) теоремы T^*.

4. Схематический очерк мемуара Эйлера[35]. Теорема T имеет такую природу, что мы можем быть уверены в ее справедливости, не давая ей безукоризненного доказательства. Тем не менее я представлю в ее пользу такие доводы, которые можно рассматривать как почти равносильные строгому доказательству.

Теорема T включает в себя бесконечное число частных случаев C₁, C₂, C₃, … Наоборот, бесконечное множество этих частных случаев C₁, C₂, C₃, … равносильно теореме T. С помощью простого вычисления мы можем узнать, верно ли C₁ или нет. Другое простое вычисление определяет, верно ли C₂, или нет, и подобным же образом для C₃ и т. д. Я проделал эти вычисления и нашел, что все C₁, C₂, C₃, …, C₄₀ верны. Достаточно предпринять эти вычисления и продолжить их сколь угодно далеко, чтобы убедиться в том, что эта последовательность, продолженная неограниченно, верна. Однако у меня нет для этого никаких других доводов, за исключением длинной индукции, которую я провел так далеко, что никоим образом не могу сомневаться в законе, для которого C₁, C₂, … являются частными случаями. Я долго тщетно разыскивало строгое доказательство теоремы T и предложил этот же вопрос некоторым из моих друзей, способности которых в этом отношении мне известны, но все согласились со мной, что теорема T верна, хотя никто не сумел раскопать какой-нибудь ключ для доказательства. Таким образом, это познанная, но все же не доказанная истина, ибо каждый из нас может в этой истине убедиться с помощью фактического вычисления сколь угодно большого числа

122

случаев C₁, C₂, C₃, …, и кажется невозможным, чтобы закон, который, как было обнаружено, выполняется, например, для 20 членов, нельзя было наблюдать и для следующих членов.

Поскольку мы таким образом обнаружили, что теорема T верна, хотя и оказалось невозможным ее доказать, все заключения, которые могут быть из нее выведены, будут той же природы, т. е. будут верны, но не доказаны. Или если бы одно из этих заключений можно было доказать, то, наоборот, можно было бы получить ключ к доказательству теоремы T; и именно с таким намерением я различными способами манипулировал теоремой T и таким путем среди других открытий нашел теорему T^*, справедливость которой должна быть столь же несомненной, как и справедливость теоремы T.

Теоремы T и T^* равносильны; они обе верны или неверны; они вместе стоят или рушатся. Подобно T, теорема T^*, включает в себя бесконечное число частных случаев C^*₁, C^*₂, C^*₃, …, и эта последовательность частных случаев равносильна теореме T^*. Здесь снова простое вычисление показывает, верно ли C^*₁, или нет. Подобным же образом можно определить, верно ли C^*₂ или нет и т. д. Нетрудно применить теорему T^* к любому данном частному случаю и таким образом всякий может убедиться в ее справедливости на стольких примерах, сколько он пожелает разобрать. И так как я должен допустить, что не в состоянии дать ей строгого доказательства, то я оправдаю ее достаточно большим числом примеров, C^*₁, C^*₂, C^*₃, … C^*₂₀. Я думаю, этих примеров достаточно, чтобы заставить любого отказаться от представления, что мое правило находится в согласии с истиной лишь по простой случайности.

Если кто-нибудь еще сомневается в том, что закон точно таков, как я указал, я приведу несколько примеров с бо́льшими числами. Путем проверки я нахожу, что C^*₁₀₁ и C^*₃₀₁ верны, и, таким образом, я нахожу, что теорема T^* справедлива даже для этих случаев, далеко отстоящих от тех, которые я проверил раньше. Эти примеры, которые я только что разобрал, безусловно рассеют любые сомнения, которые мы могли бы иметь в отношении справедливости теорем T и T^*.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ VI

Открывая свой «наиболее необычный закон чисел», Эйлер «пришел к своему заключению с помощью дифференцирований и других уловок», хотя «Исчисление Бесконечно Малых кажется неприложимым к природе целых чисел». Чтобы понять метод Эйлера, применим его к подобным же примерам. Начнем с того, что дадим название его главной «уловке», или математическому аппарату.

1. Производящие функции. Сформулируем результат п. 11 мемуара Эйлера в современных обозначениях:

123

В правой части равенства находится ряд по степеням x. Коэффициент при xⁿ в этом степенном ряде[36] есть σ(n), сумма делителей числа n. Обе части равенства представляют одну и ту же функцию от x. Разложение этой функции по степеням x «производит» последовательность σ(1), σ(2), …, σ(n), …, и потом мы называем эту функцию производящей функцией последовательности σ(n). Вообще, если

f(x) = a₀ + a₁x + a₂x² + … + a_nxⁿ + ….

то мы говорим, что f(x) есть производящая функция для a_n, или функция, производящая последовательность a₀, a₁, a₂, …, a_n, ….

Название «проводящая функция» принадлежит Лапласу[37]. Однако не давая ему названия, Эйлер пользовался аппаратом производящих функций задолго до Лапласа в нескольких сочинениях, с одним из которых мы только что познакомились в § 2. он применил этот математический аппарат к нескольким задачам комбинаторного анализа и теории чисел.

Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много маленьких предметов, что могло бы оказаться затруднительным, мы кладем их в мешок, и тогда нам нужно нести лишь один предмет, мешок. Совершенно таким же образом, вместо того чтобы иметь дело с каждым членом последовательности a₀, a₁, a₂, …, a_n, … в отдельности, мы ставим их в степенной ряд ∑ a_nxⁿ и тогда нам нужно иметь дело лишь с одним математическим объектом, степенным рядом.

2. Найдите производящую функцию для n. Или, что то же самое, найдите сумму ряда ∑ nxⁿ.

3. Дано, что f(x) — производящая функция последовательности a₀, a₁, a₂, …, a_n, … Найдите производящую функцию последовательности

0a₀, 1a₁, 2a₂, …, na_n, …

4. Дано, что f(x) — производящая функция последовательности a₀, a₁, a₂, …, a_n, … Найдите производящую функцию последовательности

0, a₀, a₁, a₂, …, a_n-1, …

5. Дано, что f(x) — производящая функция последовательности a_n. Найдите производящую функцию последовательности

s_n = a₀, + a₁, + a₂, + … + a_n.

6. Дано, что f(x) и g(x) — производящая функции, соответственно, для a_n и b_n. Найдите производящую функцию для

c_n = a₀b_n + a₁b_n-1 + a₂b_n-2 + … + a_nb₀.

7. Одна комбинаторная задача плоской геометрии. Выпуклый многоугольник с n сторонами разбивается n — 3 диагоналями на n — 2 треугольника, см. рис. 6.1. Обозначим символом D_n число различных разбиений.

Найдите D_n для n = 3, 4, 5, 6.

8 (продолжение). Нелегко на основании числовых значений рассмотренных в примере 7, угадать общее явное выражение для D_n. Однако последовательность D₃, D₄, D₅, … является «рекуррентной последовательностью» в следующем очень общем смысле: каждый ее член может быть вычислен по предыдущим членам по неизменному правилу, «рекуррентной формуле (см. мемуар Эйлера, п. 5).

124

Положите по определению D₂ = 1 и покажите, что для n ≥ 3

D_n = D₂D_n—1 + D₃D_n—2 + D₄D_n—3 + … + D _n—1D₂.

[Проверьте первые случаи. Сошлитесь на рис 6.2.].

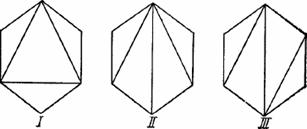
Рис. 6.1. Три типа разбиения шестиугольника[38].

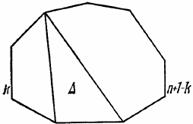
Рис. 6.2. Начало разбиения многоугольника с n сторонами.

9 (продолжение). Вывод явного выражения для D_n из рекуррентной формулы примера 8 неочевиден. Однако рассмотрите производящую функцию

g(x) = D₂x² + D₃x³ + D₄x⁴ + … + …

10. Суммы квадратов. Вспомните определение символа R_k(n) (пример 4,1), продолжите его на случай n = 0, полагая R_k(0) = 1 (разумное продолжение), введите производящую функцию

и покажите, что

[Что такое R₃(n)? Число решений уравнения

u² + v² + w² = n

в целых числах u v w, положительных, отрицательных или равных 0.

Какую роль может сыграть ряд в правой части равенства, которое требуется доказать?

Как вы представили бы правую часть равенства, которое вы собираетесь доказать? Быть может, так:

11. Обобщите результат примера 10.

125

12. Вспомните определение символа S_k(n) (пример 4.1) и выразите производящую функцию

13. Пользуясь примером 11, докажите, что R₂(n) делится на 4, R₄(n) — на 8 и R₈(n) — на 16 для n ≥ 1. (Этот результат был уже использован в гл IV, табл. II и III.)

14. Пользуясь примером 12, докажите, что

S₂(n) = 0, если n не является числом вида 8m + 2,

S₄(n) = 0, если n не является числом вида 8m + 4,

S₈(n) = 0, если n не является числом вида 8m.

15. Пользуясь примером 11, докажите, что

R_k+l(n) = R_k(0)R_l(n) + R_k(1)R_l(n — 1) + … + R_k(n)R_l(0).

16. Докажите, что

S_k+l(n) = S_k(0)S_l(n —1) + S_k(2)S_l(n — 2) + … + S_k(n —1)S_l(1).

17. Предложите простой метод для составления табл. III гл. IV по табл. I и II той же главы.

18.Пусть σ_κ(n) обозначает сумму k-х степеней делителей числа n. Например,

σ₃(15) = 1³ +3³ +5³ +15³ = 3528; σ₁(n) = σ(n).

(1) Покажите, что из предположений, найденных в § 4.6 и в примере 4.23, следует, что

σ(1)σ(2u — 1) + σ(3)σ(2u — 3) + … + σ(2u — 1)σ(1) = σ₃(u),

где u обозначает нечетное число.

(2) Численно проверьте частные случаи соотношения, найденного в (1).

(3) Какое влияние такое подтверждение оказывает на вашу веру в предположения, из которых было выведено подтвердившееся соотношение?

19. Другая рекуррентная формула. Рассмотрим производящие функции

Положим

S₄(4u) = s_u,

где u — нечетное число. Тогда в силу примеров 14 и 12

G = x + x⁹ + x²⁵ + … x(2n — 1)² + … , H = s₁x⁴ + s₃x¹² + s₅x²⁰ + … + s_{2n – 1}x^{8n — 4} + ….

Из последнего соотношения, беря логарифмы и дифференцируя, выводим, что

(x + x⁹ + x²⁵ + …)(4s₁x⁴ + 12s₃x¹² + 20s₅x²⁰ + …) =

= 4(x + 9x⁹ + 25x²⁵ + …)(s₁x⁴ + s₃x¹² + s₅x²⁰ + …).

126

Сравнивая коэффициенты при x⁵, x¹³, x²¹, … в обеих частях предыдущего равенства, после некоторых элементарных вычислений, находим следующие соотношения

0s₁ = 0,

1s₃ — 4s₁ = 0,

2s₅ — 3s₃ = 0,

3s₇ — 2s₅ — 12s₁ = 0,

4s₉ — 1s₇ — 11s₃ = 0,

5s₁₁ — 10s₅ = 0,

6s₁₃ — 1s₁₁ — 9s₇ — 24s₁ = 0,

7s₁₅ — 2s₁₃ — 8s₉ — 23s₃ = 0,

8s₁₇ — 3s₁₅ — 7s₁₁ — 22s₅ = 0,

9s₁₉ — 4s₁₇ — 6s₁₃ — 21s₇ = 0,

10s₂₁ — 5s₁₉ — 5s₁₅ — 20s₉ — 40s₁ = 0,

11s₂₃ — 6s₂₁ — 4s₁₅ — 19s₉ — 39s₃ = 0,

.................................

Самое первое уравнение этой системы бессодержательно и написано здесь только для того, чтобы подчеркнуть общий закон. Однако мы знаем, что s₁ = 1. зная s₁, из следующего уравнения мы получаем s₃. Зная s₃, из следующего уравнения получаем s₅. И так далее, из системы уравнений мы можем сколь угодно далеко вычислить члены последовательности s₁, s₃, s₅, …, один за другим, рекуррентно.

Эта система имеет замечательную структуру. Имеется 1 уравнений, содержащее 1 из величин s₁, s₃, s₅, …, 2 уравнения, содержащих 2 из них, 3 уравнения, содержащих 3 из них и т. д. Коэффициенты в каждом столбце, когда мы переходим от одной строки к следующей, возрастают на 1, а индексы — на й. первым индексом в каждом столбце является 1, а коэффициентом — 4, умноженное на первый коэффициент этой строки. Мы можем всю систему сосредоточить в одном уравнении (рекуррентной формуле); напишите ее.

20. Другой Наиболее Необычайный Закон Чисел, Относящийся к Суммам их Делителей. Если остается в силе предположение из § 4.6, то

S_2n-1 = S₄(4(2n — 1)) = σ(2n—1),

и, таким образом, пример 19 дает рекуррентную формулу, связывающую члены последовательности σ (1), σ (3), σ (5), σ (7), …, которая во многих отношениях поразительно похожа на формулу Эйлера.

Подробно выпишите и произведите численную проверку первых случаев для указанной рекуррентной формулы.

21. Для нас между рекуррентной формулой Эйлера для σ (n)(§ 2) и вышеупомянутой рекуррентной формулой для σ (2n — 1)(пример 20) существует лишь эвристическое сходство. Для нас эта последняя является предположением. Мы вывели это предположение, как Эйлер вывел свое, «с помощью дифференцирований и других уловок» из других предположений.

Покажите, что рекуррентная формула для σ (2n — 1), указанная в примере 20, равносильна равенству

S₄(4(2n — 1)) = σ(2n—1),

К которому мы пришли в § 4.6, т. е. если одно из этих двух утверждений верно, то непременно верно и другое.

22. Обобщите пример 19.

23. Придумайте метод для вычисления R₈(n) независимо от R₄(n).

127

24. Как Эйлер упустил открытие. Метод, иллюстрированный примерами 19 и 23 и в общем виде высказанный в примере 22, принадлежит Эйлеру[36]. Придумывая этот метод, Эйлер имел целью задачу о четырех квадратах и некоторые связанные с ней задачи. В самом деле, он применил свой метод к задаче о четырех квадратах и индуктивно исследовал число представлений, но ему не удалось открыть замечательный закон, управляющий R₄(n), который в конце концов не так уж трудно индуктивно обнаружить (примеры 4.10 — 4.15). Как это случилось?

Исследуя уравнение

n = x² + y² + z² + w²,

мы можем выбрать различные точки зрения, в частности следующие:

(1) Допустить в качестве x, y, z и w только неотрицательные целые числа.

(2) Допустить в качестве x, y, z и w все целые числа, положительные, отрицательные и нуль.

Вторая точка зрения, быть может, менее очевидна, но приводит к R₄(n) и к замечательной связи между R₄(n) и делителями числа n. Первая точка зрения более очевидна, но число решений, по-видимому, не имеет никакого простого замечательного свойства. Эйлер выбрал точку зрения (1), а не точку зрения (2); он применил свой метод, объясненный в примере 22, к выражению

(1 + x+ x⁴ + x⁹ +…)⁴,

а не к выражению

(1 + 2x+ 2x⁴ + 2x⁹ +…)⁴,

и таким образом прошел мимо большого открытия. Поучительно сравнить два направления исследования, которые кажутся такими похожими вначале, но одно из которых удивительно плодотворно, а другое почти совершенно бесплодно.

Свойства R₄(n), S₄(n), R₈(n) и S₈(n), исследованные в гл. IV (примеры 4.10 — 4.15, §§ 4.3 — 4.6, примеры 4.18—4.23), были открыты Якоби не индуктивно, но как случайные следствия его исследований об эллиптических функциях. С тех пор было найдено несколько доказательств этих теорем, но ни одно известное доказательство не является вполне элементарным и прямым[37].

25. Обобщение теоремы Эйлера о σ(n). Для данного k положите

и покажите, что для n = 1, 2, 3, …

Какой частный случай дает теорему Эйлера из § 2?

VII. МАТЕМАТИЧЕСКАЯ ИНДУКЦИЯ

Метод Якова Бернулли имеет значение и для естествознания. Он учит нас, что свойство A, найденное при помощи неполной индукции в членах C₁, C₂, C₃, … понятия B, можно только в том случае приписать самому этому понятию, если констатировано, что это свойство связано с признаками понятия B и от изменений его членов не зависит. Как во многих других случаях, математика и здесь является образцом для естествознания. — Эрнст Мах[38]

1. Индуктивная фаза. Опять мы начинаем с примера.

Совсем нетрудно найти сумму первых n целых чисел. Формулу

которую можно открыть и доказать многими способами, мы будем считать известной[39]. Труднее найти формулу для суммы n первых квадратов

1 + 4 +9 +16 + … + n².

Нетрудно вычислить эту сумму для малых значений n, но уловить правило нелегко. Вполне естественно, однако, попытаться обнаружить какого-то рода параллелизм между этими двумя суммами и рассмотреть их совместно:

n	1	2	3	4	5	6	…
1 + 2 + … + n	1	3	6	10	15	21	…
1^2 + 2^2 + … + n^2	1	5	14	30	55	91	…

129

Как связаны две последние строки? Нам может прийти в голову исследовать их отношение

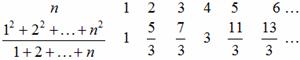
Здесь правило очевидно, и, если отношения из второй строки записать следующим образом:

его почти невозможно не заметить. Едва ли мы сможем удержаться и не сформулировать предположение, что

Пользуясь значением знаменателя в левой части, которое мы считаем известным, можем высказать наше предположение в форме

Верно ли это? То есть всегда ли это верно? Формула, конечно, верна в частных случаях n = 1, 2, 3, 4, 5, 6, из которых она возникла. Верна ли она и в следующем случае n = 7? Предположение приводит нас к предсказанию, что

и действительно, обе части оказываются навными 140.

Мы могли бы, конечно, перейти к следующему случаю n = 8 и проверить его, но соблазн не так уж велик. Так или иначе мы склонны верить, что формула подтвердится и в следующем случае, и, таким образом, это подтверждение увеличило бы нашу уверенность, номало, так мало, что едва ли стоит тратить время на вычисления[39]. Как мы могли бы испытать наше предположение с бо́льшим эффектом?

Если предположение верно при любом n, то оно должно было бы не зависеть от изменения случаев, оно должно сохраняться при переходе от одного случая к другому. Предположительно,

Однако если эта формула верна при любом n, то она должна быть справедлива и для следующего n:мы должны иметь

130

Вот возможность серьезно проверить предположение: вычитая почленно из нижней строки верхнюю, получаем

Верно ли это следствие из нашего предположения?

Небольшое преобразование правой части дает

Рассматриваемое следствие неоспоримо верно, предположение прошло суровое испытание.

2. Фаза доказательства. Подтверждение любого следствия увеличивает нашу веру в предположение, но подтверждение только что рассмотренного следствия может сделать больше: оно может предположение доказать. Нужно лишь немного изменить нашу точку зрения и переставить наши замечания.

Предположительно верно, что

Неоспоримо верно, что

Следовательно, верно, что

(мы сложили два предыдущих неравенства). Это означает: Если наше предположение верно для некоторого целого числа n, то оно непременно остается верно для следующего целого числа n +1.

Однако мы знаем, что предположение верно для n = 1, 2, 3, 4, 5, 6, 7. Будучи верным для 7, оно должно быть верным и для следующего числа 8; будучи верным для 8, оно должно быть верно и для 9; так как оно верно для 9, оно верно и для 10, а значит, и для 11 и т. д. Предположение верно для всех целых чисел; нам удалось доказать его в полной общности.

3. Исследование переходов. Последнее рассуждение предыдущего параграфа может быть немного упрощено. О предположении достаточно знать две вещи:

131

Оно верно для n = 1.

Если оно верно для n, то оно также верно и для n + 1.

Тогда предположение верно для всех целых чисел: верно для 1, следовательно, и для 2; верно для 2, следовательно, и для 3 и т. д.

Мы здесь имеем фундаментально важный прием доказательства. Мы могли бы назвать его «переходом от n к n + 1», но обычно его называют «математической индукцией». Этот обычный термин является очень неподходящим названием для приема доказательства, так как индукция (в смысле, в котором этот термин чаще всего употребляется) дает только правдоподобие, а не доказательное умозаключение.

Имеет ли математическая индукция какое-нибудь отношение к индукции? Да, имеет, и мы рассматриваем ее здесь по этой причине, а не только из-за ее названия.

В приведенном нами примере доказательное рассуждение § 2 естественно завершает индуктивное рассуждение § 1, и это типично. Доказательство § 2 выступает как «математическое дополнение к индукции», и если слова «математическая индукция» мы возьмем в этом смысле в качестве сокращения, то этот термин в конечном счете может оказаться вполне подходящим. (Возьмем их поэтому в этом смысле, не расходясь с установившейся математической терминологией.) Математическая индукция часто возникает как заключительный шаг или последняя фаза индуктивного исследования, и в этой последней фазе часто используются наводящие соображения, возникшие в предыдущих фазах.

На другой и еще лучший повод для рассмотрения в настоящем контексте математической индукции намекает приведенная в начале этой главы выдержка из книги Эрнста Маха[40]. Исследуя предположение, мы рассматриваем различные случаи, к которым это предположение должно быть применимо. Мы хотим увидеть, чвляется ли соотношение, утверждаемое предположением, устойчивым, т. е. независимым от изменения случаев, не нарушаемым таким изменением. Наше внимание, таким образом, естественно, обращается к переходу от одного такого случая к другому. «Что посредством центростремительной силы планеты могут удерживаться на некоторых орбитах,

132

мы можем легко понять, если рассмотрим движение брошенных тел», сказал Ньютон, и затем он вообразил камень, который бросают со все большей и большей начальной скоростью до тех пор, пока его траектория не обойдет вокруг Земли, как траектория Луны; см. пример 2.18 (4). Итак, Ньютон ясно себе представляет непрерывный переход от движения брошенного тела к движению планеты. Он рассматривает переход между двумя случаями, к которым закон всемирного тяготения, доказательство которого он предпринял, должен быть одинаково применим. Любой начинающий, пользующийся математической индукцией для доказательства какой-нибудь элементарной теоремы, поступает в этом отношении подобно Ньютону: он рассматривает переход от n к n + 1, переход между двумя случаями, к которым доказываемая теорема должна быть одинаково применима[41].

4. Техника математической индукции. Для того чтобы быть хорошим математиком или хорошим игроком в карты или хорошим специалистом в любой области, вы должны уметь хорошо догадываться. Для того чтобы уметь хорошо догадываться, вы должны, я бы полагал, прежде всего иметь природные способности. Однако иметь природные способности недостаточно. Вы должны исследовать ваши догадки, сравнивать их с фактами, видоизменять их, если необходимо, и, таким образом, приобрести широкий (и глубокий) опыт в догадках, которые не оправдались, и в догадках, которые сбылись. С таким опытом в своем подсознании вы, возможно, сумеете

133

более основательно судить о том, какие догадки могут оказаться правильными, а какие нет.

Математическая индукция является приемом доказательства, часто полезным для подтверждения математических предположений, к которым мы пришли с помощью некоторого процесса индукции. Поэтому если мы хотим приобрести опыт в индуктивном математическом исследовании, то желательно некоторое знакомство с техникой математической индукции.

Настоящий параграф и нижеследующие примеры и примечания могут оказать небольшую помощь в овладении этой техникой.

(1) Индуктивная фаза. Начнем с примера, очень похожего на пример, разобранный в §§ 1 и 2. мы хотим в какой-либо более короткой форме выразить следующую сумму, связанную с первыми n квадратами:

Вычислим эту сумму в первых нескольких случаях и составим таблицу результатов:

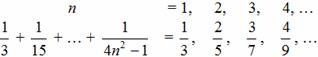
Возникает очевидная догадка:

На основании нашего опыта, приобретенного при решении предыдущей сходной задачи, мы сразу же испытаем наше предположение с наибольшим возможным эффектом: испытаем переход от n к n + 1. Если наше предположение верно всегда, то оно должно быть верно и для n, и для n + 1.:

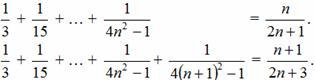
Вычитая, получаем

Верно ли это следствие из нашего предположения? Преобразуем обе части, стараясь подвести их ближе одну к другой:

134

Простое алгебраическое преобразование показывает, что обе части действительно тождественны. Рассмотренное следствие неоспоримо верно.

(2) Фаза доказательства. Теперь переставим наши замечания, как в предыдущем примере, § 2.

Предположительно

Неоспоримо

Следовательно

Предположение, если допустить, что оно верно для n, оказалось верным и для n + 1. Поскольку оно верно для n = 1, оно верно для любого n.

(3) Короче. Мы могли бы затратить немного меньше времени на индуктивную фазу нашего решения. Сделав предположение, мы могли подозревать, что его удастся доказать с помощью математической индукции. Затем, без какой бы то ни было проверки, мы могли бы попытаться непосредственно применить математическую индукцию следующим образом:

Предположительно

Следовательно,

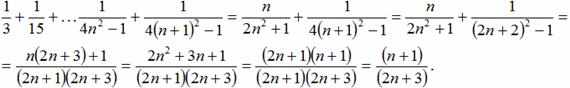
Итак, нам удалось вывести для n + 1 соотношение, предложенное нами для n. Это в точности то, что требовалось сделать, и, таким образом, мы доказали наше предположение.

135

В этом варианте решения меньше повторений, но, пожалуй, он является и несколько менее естественным, чем изложенный в (1) и (2).

(4) Еще короче. Мы можем увидеть решение почти с первого взгляда, если заметим, что

(Если мы знакомы с разложением рациональной функции на элементарные дроби, то к этой формуле мы приходим совершенно естественно.) полагая n = 1, 2, 3, …, n и складывая, получаем

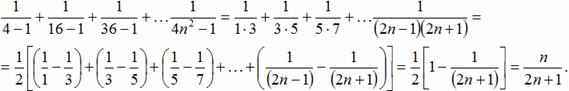
То, что сейчас произошло, происходит не так уж редко. Теорема, доказанная с помощью математической индукции, часто может быть короче доказана каким-либо другим методом. К такому сокращению может даже привести тщательное исследование доказательства с помощью математической индукции.

(5) Другой пример. Рассмотрим два числа, a и b, удовлетворяющие неравенствам

0 < a < 1, 0 < b < 1.

Тогда, очевидно,

(1 — a) (1 — b) = 1 — a— b + ab > 1 — a— b.

Естественное обобщение заставляет нас подозревать, что верно следующее утверждение: Если n ≥ 2 и 0 < a₁ < 1, 0 < a₂ < 1, …, < 1, 0 < a_n < 1, …, то

(1 — a₁) (1 — a₂) … (1 — a_n) > 1 — a₁ — a₂ — … — a_n.

Докажем его, пользуясь математической индукцией. Мы видели, что это неравенство верно в первом случае, для которого, как утверждается, оно применимо, — для n = 2. поэтому, допустив, что оно верно для n, где n ≥ 2, мы должны вывести его для n + 1.

136

Предположительно

(1 — a₁) … (1 — a_n) > 1 — a₁ — … — a_n.

и мы знаем, что

0 < a_n+1 < 1.

Следовательно,

(1 — a₁) … (1 — a_n) (1 — a_n+1) > (1 — a₁ — … — a_n) (1 — a_n+1) =

= 1 — a₁ — … — a_n — a_n+1 + (a₁ + … + a_n) a_n+1 >1 — a₁ — … — a_n — a_n+1.

Мы вывели для n + 1 то, что предположили для n: доказательство закончено.

Отметим, что математической индукцией можно пользоваться и для доказательства предложений, которые применимы не к абсолютно всем натуральным числам, а ко всем натуральным числам, начиная с некоторого. Например, только что доказанная теорема относится к значениям n ≥ 2.

(6) Что такое n? Рассмотрим теперь одну теорему плоской геометрии.

Если выпуклый многоугольник P содержится в многоугольнике Q, то периметр P меньше, чем периметр Q.

То, что площадь многоугольника P меньше, чем площадь внешнего многоугольника Q, очевидно. Но сформулированная теорема совсем не так очевидна; без ограничения, что P — выпуклый многоугольник, она была бы неверна.

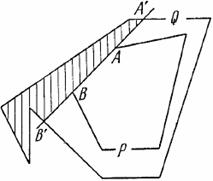
Рис. 7.1. От n к n + 1.

Рис. 7.1. показывает существенную идею доказательства. Мы отрезаем от внешнего многоугольника Q заштрихованный кусок; остается новый многоугольник Q′, часть Q, обладающий двумя свойствами.

Во-первых, Q′ еще содержит выпуклый многоугольник P, который будучи выпуклым, целиком лежит по одну сторону от прямой A′B′, полученной в результате продолжения стороны AB, полученной в результате продолжения стороны AB многоугольника P.

Во-вторых, периметр Q′ короче, чем периметр Q. Действительно, периметр Q′ отличается от периметра Q лишь постольку, поскольку первый содержит прямолинейный отрезок, соединяющий точки A′ и ′B, а второй вместо него содержит ломаную линию, содержащую эти точки (на дальней стороне заштрихованного куска). Однако прямая линия есть кратчайшее расстояние между точками A′ и ′B.

Как мы перешли от Q к Q′, так мы можем перейти от Q′ к другому многоугольнику Q″. Таким образом, мы получаем последовательность многоугольников Q, Q′, Q″, … Каждый многоугольник

137

содержится в предыдущем и имеет более короткий периметр, а последним многоугольником в этой последовательности будет P. Следовательно, периметр короче, чем периметр Q.

Нам следует распознать природу предыдущего доказательства; в действительности оно является доказательством с помощью математической индукции. Но что такое n? По отношению к какой величине совершается индукция?

Это серьезный вопрос. Математическая индукция применяется в различных областях и иногда в очень трудных и запутанных вопросах. Пытаясь найти скрытое доказательство, мы можем встретиться с решающим вопросом: что должно играть роль n? По отношению к какой величине нам следует попытаться провести математическую индукцию?

В предыдущем доказательстве в качестве n целесообразно выбрать число тех сторон внутреннего выпуклого многоугольника, которые целиком не принадлежат к периметру внешнего многоугольника. Рис 7.2 иллюстрирует случай n = 1. Я предоставляю читатель выяснить, что целесообразно называть n на рис. 7.1.

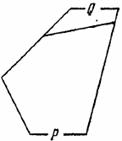
Рис. 7.2 Случай n = 1.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ VII

1. Заметьте, что

1	=	1,
1 — 4	=	— (1 + 2)
1 — 4 + 9	=	1 + 2 + 3
1 — 4 + 9 — 16	=	— (1 + 2 + 3 + 4).

Догадайтесь, к какому общему закону подводят эти примеры, выразите его в подходящих математических обозначениях и докажите.

2. Докажите выражающие L_n, S_n и S_n в явном виде формулы, догадку о которых мы высказали соответственно в примерах 3.13, 3.14 и 3.20. [Примеры 3.11, 3.12)]

3. Найдите выражение для

1³ + 2³ + 3³ + … + n³

и докажите его с помощью математической индукции. (Пример 1.4)

4. Найдите выражение для

справедливое для n ≥ 2, и докажите его с помощью математической индукции.

5. Найдите выражение для

справедливое для n ≥ 1, и докажите его с помощью математической индукции.

138

6. Обобщите соотношение

и докажите ваше обобщение с помощью математической индукции.

7. Рассмотрим операцию, состоящую в переходе от последовательности

a₁, a₂, a₃, … a_n, …

к последовательности

s₁, s₂, s₃, … s_n, …

с общим членом

s_n = a₁ + a₂ + a₃ + … + a_n.

Мы будем называть эту операцию (образование последовательности s₁, s₂, s₃, …) «суммированием последовательности a₁, a₂, a₃, …». В этой терминологии мы можем следующим образом выразить уже замеченный (в примере 1.3) факт:

Вы можете от последовательности всех натуральных чисел 1, 2, 3, 4, … перейти к последовательности квадратов 1, 4, 9, 16, … в два шага (1) отбросить каждый второй член, (2) суммировать о ставшуюся последовательность. В самом деле, взгляните на таблицу[40]

1	2	3	4	5	6	7	8	9	10	11	12	13…
1		3		5		7		9		11		13…
1		4		9		16		25		36		49

Докажите это утверждение с помощью математической индукции.

8 (продолжение). Вы можете от последовательности всех натуральных чисел 1, 2, 3, 4, … перейти к последовательности кубов 1, 8, 27, 64, … в четыре шага: (1) отбросить каждый третий член, (2) суммировать оставшуюся последовательность, (3) отбросить каждый второй член, (4) суммировать оставшуюся последовательность. После того как исследуете таблицу

1	2	3	4	5	6	7	8	9	10	11	12	13…
1	2		4	5		7	8		10	11		13…
1	3		7	12		19	27		37	48		61…
1			7			19			37			61…
1			8			27			64			125…

докажите это с помощью математической индукции.

9 (продолжение). Вы можете от последовательности всех натуральных чисел 1, 2, 3, 4, … перейти к последовательности четвертых степеней 1, 16, 81, 256, … в шесть шагов, которые видны из таблицы

1	2	3	4	5	6	7	8	9	10	11	12	13…
1	2	3		5	6	7		9	10			13…
1	3	6		11	17	24		33	43			67…
1	3			11	17			33	43			67…
1	4			15	32			65	108			175…
1				15				65				175…
1				16				81				256…

О чем говорят эти факты?

139

10. Замечая, что

					=	1,
1					=	— 4,
1 — 5	+ 10				=	6,
1 — 5	+ 10	— 10			=	— 4,
1 — 5	+ 10	— 10	+ 5		=	1,
1 — 5	+ 10	— 10	+ 5	— 1	=	0,

приходим к общему утверждению:

для

0 < k < n, n = 1, 2, 3, …

Доказывая это с помощью математической индукции, предпочтете ли вы переходить от n к n + 1 или же от k к k +1.

11.В теннисном турнире имеется 2n участников. В первом круге турнира каждый участник играет ровно один раз, так что всего проводится n игр, в каждой из которых занято два игрока. Покажите, что пары для первого круга могут быть составлены точно

1·3·5·7 … (2n — 1)

различными способами.

12. Доказать больше иногда легче. Пусть

и определим последовательность f₀(x), f₁(x), f₂(x), … условием, что

для n = 0, 1, 2, 3, … (Такое определение называется рекуррентным: чтобы найти f₁(x), мы должны возвратиться к f₁.) Замечая, что

докажите с помощью математической индукции, что для n ≥ 1 числитель f_n(x) есть многочлен, свободный член которого равен 0, а другие коэффициенты — натуральные числа.

13 (продолжение). Найдите с помощью индукции и докажите с помощью математической индукции дальнейшие свойства функции f_n(x).

14. Уравновесьте вашу теорему! Типичное предложение A, доступное доказательству с помощью математической индукции, имеет бесконечное множество случаев A₁, A₂, A₃, … A_n, … случай A₁ часто является легким; как бы то ни было, A₁, должен поддаваться определенным средствам. Раз A₁ установлен, нам нужно, предполагая A_n, доказать A_n+1. Предложение A′, более сильное, чем A, иногда доказать легче, чем A[42]. Действительно, пусть A′ состоит из случаев A′₁, A′₂, A′₃, … A′_n, … Переходя от A к A′, мы делаем груз доказательства более тяжелым: вместо A_n+1 мы должны доказать более сильное A′_n+1. Однако мы делаем и опору для доказательства более крепкой: вместо A_n мы можем пользоваться дающим больше информации A′_n. Это иллюстрируется

140

решением примера 12. Однако мы сделали бы это решение бесполезно громоздким, включив материал, рассмотренный в примере 13, к которому удобнее подойти как к следствию с помощью дополнительных замечаний.

Вообще, когда вы пытаетесь придумать доказательство с помощью математической индукции, вам оно может не удаваться по двум противоположным причинам. Оно может вам не удаваться и потому, что вы пытаетесь доказать слишком мало: ваше A_n — слишком слабая опора. Вы должны уравновесить утверждение вашей теоремы так, чтобы опора была как раз достаточна для груза. И таким образом механизм доказательства приближает вас к более уравновешенному, более приспособленному взгляду на эти факты. Это можно считать типичным для роли доказательств в создании науки.

15. Перспектива. Более сложные задачи в более трудных областях требуют более усложненной техники математической индукции и ведут к различным видоизменениям этого важного метода доказательства. Некоторые из наиболее замечательных примеров дает теория групп. Интересным вариантом является «обратная математическая индукция», или «заключение от n к n — 1»; интересный элементарный пример см. в книге Харди Г. Г., Литтлвуд Дж. Е. и Полиа Г. Неравенства, М., 1948, стр. 30 и 33.

16. Дано, что Q₁ = 1 и

для n = 2, 3, … Найдите общее выражение для Q_n и докажите, что оно верно.

17. Равны ли любые n чисел? Вы сказали бы «Нет». Все же мы можем попытаться с помощью математической индукции доказать обратное. Более заманчиво, однако, доказать утверждение: «у любых n девушек глаза одинакового цвета».

Для n = 1 утверждение, очевидно, верно (или «бессодержательно»). Остается перейти от n к n + 1. Для определенности я перейду от 3 к 4, а общий случай оставлю вам. Позвольте представить вас четырем девушкам: Анне, Бэле, Вере и Галине, или, для краткости, А, Б, В и Г. Предполагается (n = 3), что глаза девушек А, Б и В одинакового цвета. Точно так же, по предположению, и глаза девушек Б, В и Г одинакового цвета (n = 3). Следовательно, глаза всех четырех девушек А, Б, В и Г должны быть одинакового цвета; для полной ясности можно взглянуть на диаграмму

Это доказывает утверждение для n + 1 = 4, а переход, например, от 4 к 5, очевидно, не более труден.

Объясните парадокс. Можете испытать экспериментальный подход, посмотрев в глаза нескольким девушкам.

18. Если параллельные прямые рассматривать как пересекающиеся (в бесконечности), то утверждение «любые n прямых на плоскости имеют общую точку» верно для n = 1 («бессодержательно») И для n = 2 (благодаря нашей интерпретации). Постройте (парадоксальное) доказательство с помощью математической индукции.

VIII. МАКСИМУМЫ И МИНИМУМЫ

Так как здание всего мира совершенно и возведено премудрым Творцом, то в мирен не происходит ничего, в чем не был бы виден смысл какого-нибудь максимума или минимума. — Эйлер[43]

1. Схемы. Задачи, относящиеся к наибольшим и наименьшим значениям, или задачи на максимум и минимум, пожалуй, более привлекательны, чем другие математические задачи сравнимой трудности, и это, быть может, имеет совсем простые причины. У каждого из нас есть свои личные задачи. Мы можем заметить, что эти задачи очень часто являются своего рода задачами на максимум или минимум. Мы хотим получить определенный предмет за наиболее низкую возможную цену, или наибольший возможный эффект при определенном усилии, или максимальную работу, произведенную за данное время, и, конечно, хотим как можно меньше рисковать. Математические задачи на максимум привлекают нас, я думаю, потому, что они идеализируют наши повседневные задачи.

Мы даже склонны воображать, что Природа действует как хотелось бы действовать нам, получая наибольший эффект с наименьшим усилием. Физикам удалось дать идеям этого рода ясные и полезные формы; они описывают некоторые физические явления в терминах «принципов минимума». Первый динамический принцип этого типа («принцип наименьшего действия», обычно именуемый принципом Мопертюи) был, в сущности, развит Эйлером; его слова, приведенные в начале этой главы, ярко описывают определенный взгляд на задачи о максимуме и минимуме, которые в его век могли привлекать многих ученых.

В следующей главе мы рассмотрим несколько задач на максимум и минимум, возникающих в элементарной физике. Настоящая глава подготовит нас к следующей.

Дифференциальное исчисление дает общий метод для решения задач на максимум и минимум. Мы здесь не будем пользоваться

142

этим методом. Будет более поучительно развить вместо него несколько наших собственных «схем».

Решив задачу с настоящим пониманием и интересом, вы приобретаете драгоценное имущество: схему, модель, которой вы можете подражать при решении сходных задач. Вы развиваете эту схему, если, следуя ей, достигаете успеха, если размышляете над причинами вашего успеха, над аналогией решенных задач, над относящимися к делу обстоятельствами, которые делают вашу задачу доступной этого рода решению и т. д. Развивая такую схему, вы сможете в конце концов прийти к настоящему открытию. Во всяком случае у вас есть возможность приобрести некоторые находящиеся в хорошем порядке и легко доступные знания.

2. Пример. На плоскости даны две точки и прямая, причем обе точки лежат по одну сторону от прямой. На данной прямой найти точку, из которой отрезок, соединяющий две данные точки, виден под наибольшим возможным углом.

Рис. 8.1. Отыскание наилучшего вида.

Рис. 8.2. Изменение угла может выглядеть приблизительно так.

Это — задача, которую мы хотим решить. Начертим фигуру (рис. 8.1) и введем подходящие обозначения. Пусть A и B — две данные точки,

l — данная прямая,

X — переменная точка прямой l.

Рассмотрим ∠ AXB, угол с вершиной в переменной точке X, стягиваемый данным отрезком AB. Требуется найти такое положение точки X на данной прямой l, для которого этот угол достигает своего максимума.

Представьте себе, что l — прямая дорога. Если из некоторой точки дороги l вы хотите выстрелить в цель, простирающуюся от A до B, то вам следовало бы выбрать ту точку, которую мы разыскиваем: она дает нам наилучшую возможность попасть в цель. Если у вас более мирное намерение сделать с дороги снимок фасада, углы которого находятся в A и B, то вы должны были бы снова выбрать ту точку, которую мы разыскиваем; она даст вам наиболее широкое поле зрения.

143

Решение нашей задачи не совсем непосредственно. Но, даже если мы не знаем, где достигается максимум, мы не сомневаемся в том, что он где-нибудь достигается. Почему это так правдоподобно?

Мы сумеем объяснить это правдоподобие если ясно представим себе изменение угла, максимум которого мы пытаемся найти. Вообразим, что мы идем по прямой l и смотрим на отрезок AB. Начнем с точки, в которой прямая l и прямая, проходящая через A и B, пересекаются, и пойдем вправо. Вначале угол, под которым виден отрезок AB, равен нулю; затем угол возрастает; однако в конце концов, когда мы будем находиться очень далеко от AB, он снова должен убывать, так как он обращается в нуль на бесконечном расстоянии[44]. Между двумя крайними случаями, в которых угол равен нулю, он должен где-нибудь стать максимальным. Но где?

На этот вопрос нелегко ответить хотя мы могли бы указать большие отрезки прямой l, где максимум, вероятно, не достигается. Выберем любую точку на нашей прямой и обозначим ее через X. Очень вероятно, что эта точка, выбранная наугад, не находится в положении максимума, которое мы пытаемся найти. Как мы могли бы с полной ясностью решить, находится ли она в положении максимума или нет?

Рис. 8.3. Касательная линия уровня.

Довольно легко заметить одно обстоятельство[45]. Если точка не находится в положении максимума то должна существовать другая точка, по другую сторону от положения максимума, в которой рассматриваемый угол имеет то же самое значение. Существует ли на прямой l какая-нибудь другая точка X′, из которой отрезок AB виден под тем же углом, как и из точки X? Вот наконец вопрос, на который мы легко можем ответить. В силу известного свойства углов, вписанных в окружность (Евклид, III, 21), и X, и X′ (если точка X′ существует) должны находиться на одной и той же окружности, проходящей через точки A и B.

А теперь может возникнуть идея. Проведем несколько окружностей, проходящих через данные точки A и B. Если такая окружность пересекает прямую l в двух точках, как например X и X′ на рис. 8.3, то отрезок AB виден из обеих точек X и X′ под одним

144

и тем же углом, но этот угол не является наибольшим возможным углом: окружность, пересекающая l между X и X′, дает бо́льший угол. Пересекающие окружности не могут дать наибольшего угла: вершина максимального угла есть точка, в которой окружность, проходящая через A и B, касается прямой l (точка M на рис. 8.3).

3. Схема касательной линии уровня. Снова просмотрим только что найденное решение. Чему мы можем на нем научиться? Что в нем существенно? Какие черты допускают подходящее обобщение?

Шаг, который после некоторого размышления кажется наиболее существенным, не слишком бросается в глаза. Я думаю, что решающим шагом явилось расширение нашей точки зрения, выход из прямой l, рассмотрение значений величины, максимум которой мы разыскиваем (угла, стягиваемого отрезком AB) в точках плоскости, лежащих вне l. Мы рассмотрели изменение этого угла, когда его вершина движется по плоскости, рассмотрели зависимость этого угла от положения его вершины. Короче, мы представили себе этот угол как функцию переменной точки (его вершины) и стали считать эту точку (вершину), изменяющейся на плоскости.

Угол остается постоянным, когда его вершина движется по дуге окружности, соединяющей точки A и B. Назовем такую дугу окружности линией уровня. Это выражение подчеркивает общую точку зрения, к которой мы собираемся прийти. Линии, вдоль которых функция от переменной точки остается постоянной, обычно называются линиями уровня этой функции.

Однако не забудем, что́ в нашей задаче нужно было определить. Нам требовалось найти максимум угла (этой функции от переменной точки), когда его вершина (переменная точка) не может свободно двигаться по плоскости, а ограничена предписанным путем, прямой l. В какой точке предписанного пути достигается максимум?

Мы уже знаем ответ, но постараемся лучше его понять, посмотрим на него с более общей точки зрения. Рассмотрим аналогичный, довольно общий и очень много говорящий нашей интуиции пример.

Вы знаете, что представляют собою на карте или на местности (мы будем иметь в виду холмистую страну), которую изображает эта карта, «линии уровня», или «контурные линии». Они являются линиями постоянной высоты; линия уровня связывает те точки на карте, которые изображают точки земной поверхности, находящиеся на одинаковой высоте над уровнем моря. Если вы вообразите, что море поднялось на 100 метров, то при новом уровне моря появится новая береговая линия с заливами, вторгшимися в долины. Эта новая береговая линия есть линия уровня высоты 100. Картограф наносит на карту только несколько линий уровня с постоянными интервалами, например с высотой 100, 200, 300, … ; однако существует линия уровня для каждой высоты, так что через каждую точку местности проходит некоторая линия уровня. Высота над уровнем

145

моря есть функция от переменной точки, вот что важно для картографа или для вас, когда вы передвигаетесь по местности; эта функция остается постоянной вдоль каждой линии уровня.

Вот теперь задача, аналогичная нашей только что рассмотренной (в § 2) задаче. Вы идете по дороге, по предписанному пути. В какой точке дороги вы достигнете максимальной высоты над уровнем моря?

Очень легко сказать, где вы ее не достигнете. Точка, которую вы проходите, поднимаясь или спускаясь, конечно, не является ни точкой максимальной высоты, ни точкой минимальной высоты. В такой точке ваша дорога пересекает линию уровня: максимум (или минимум). НЕ может достигаться в точке, где предписанный путь пересекает линию уровня.[41]

После этого существенного замечания возвратимся к нашему примеру (§ 2, рис. 8.1, 8.2, 8.3). Рассмотрим весь предписанный путь: часть прямой l, простирающуюся от точки ее пересечения с прямой, проходящей через A и B, на бесконечное расстояние (вправо). В каждой своей точке этот предписанный путь пересекает линию уровня (дугу окружности с концами в A и B), за исключением только одной точки, где он касается линии уровня (такой окружности). Если где-нибудь есть максимум, то он должен быть в этой точке: в точке максимума предписанный путь касается линии уровня.

Это — очень сильный намек на общую идею, скрывающуюся за нашим примером. Исследуем, однако, этот намек. Применим эту идею к простому аналогичному случаю и посмотрим, как она позволяет решить задачу. Вот легкий пример.

На данной прямой найти точку, находящуюся на наименьшем расстоянии от данной точки.

Введем подходящие обозначения:

A — данная точка,

a — данная прямая.

Подразумевается, что данная точка A не лежит на данной прямой a. Требуется найти кратчайшее расстояние от A до a.

Решение знает каждый. Вообразите, что вы плаваете в спокойном море; в этот момент вы находитесь в точке А; линия а отмечает совершенно прямой берег. Внезапно вы пугаетесь, вы хотите как можно быстрее достичь твердой земли. Где ближайшая точка берегат Вы это знаете без размышления. Это знала бы и собака. Собака или корова, брошенные в воду, без промедления начинают плыть по перпендикуляру от А к а.

Однако наша цель состоит не только в том, чтобы найти решение, но и в том, чтобы исследовать общую идею, позволяющую его найти. Величина, минимум которой мы хотим отыскать, есть расстояние от переменной точки до данной точки A. Это расстояние зависит от положения переменной точки. Линии уровня этого расстояния, очевидно, являются концентрическими окружностями с общим центром A. «Предписанный путь» есть данная прямая a. В точке,

146

где предписанный путь пересекает линию уровня, минимум не достигается. В действительности он достигается в (единственной) точке, в которой предписанный путь касается линии уровня (в точке M на рис. 8.4). Кратчайшее расстояние от точки A до прямой а есть радиус окружности с центром A, касающейся a, что мы и знали сначала. Все же мы кое-чему научились. Общая идея кажется теперь более ясной, и сделать ее совершенно ясной можно предоставить читателю.

Отчетливо запомнив общие черты предыдущих задач, естественно постараться подыскать аналогичные задачи, к которым мы могли бы применить такую же схему решения. Раньше мы рассматривали переменную точку на плоскости и отыскивали минимум или максимум функции от такой точки на предписанном пути. Мы смогли бы, однако, рассматривать переменную точку в пространстве и отыскивать минимум или максимум функции на предписанной поверхности. На плоскости особую роль играли касательные линии уровня. Аналогия побуждает нас ожидать, что подобную роль в пространстве будут играть касательные поверхности уровня.

Рис. 8.4. Другая касательная линия уровня.

Рис. 8.5. Две скрещивающиеся прямые.

4. Примеры. Рассмотрим два примера, которые могут быть решены одним и тем же методом, но в остальном имеют очень мало общего.

(1) Найти наименьшее расстояние между двумя данными скрещивающимися прямыми.

Введем обозначения:

a и b — две данные скрещивающиеся прямые,

X — переменная точка на прямой a,

Y — переменная точка на прямой b;

см. рис. 8.5. Требуется определить такое положение прямолинейного отрезки XY; при котором он является наиболее коротким.

Расстояние XY зависит от положений двух концов X и Y отрезка XY; причем оба они являются переменными. Имеются две переменные точки, а не всего лишь одна, и в этом характерная трудность задачи. Если бы одна из этих двух точек была задана, фиксирована, постоянна, а изменялась только другая, то задача была

147

бы легкой. Фактически она даже не была бы новой; она совпала бы с только что решенной задачей (§ 3).

Фиксируем на время одну из первоначально переменных точек, скажем Y. Тогда отрезок XY будет расположен в плоскости, проходящей через фиксированную точку Y. и данную прямую a, и только один из его концов, X, будет переменным, пробегающим вдоль прямой a. Очевидно, длина отрезка XY будет минимальной, когда он станет перпендикулярным к a (в силу § 3, рис. 8.4).

Но мы могли бы поменять роли двух точек X и Y. Фиксируем теперь для разнообразия Х и сделаем переменной лишь точку Y. Очевидно, отрезок XY становится наиболее коротким, когда он перпендикулярен к b.

Положение минимума отрезка XY не зависит, однако, от нашей прихоти и от того, какую роль мы приписываем точкам X и Y, потому у нас возникает подозрение, что в этом положении отрезок перпендикулярен и к a, и к b. Взглянем все же более внимательно на эту ситуацию.

В действительности предыдущее доказательство прямо показывает, где положение минимума не может находиться (и только косвенно, где оно должно было бы находиться). Я утверждаю, что положение, в котором отрезок XY не перпендикулярен к примой a в точке X, не является положением минимума. В самом деле, я зафиксирую точку Y и передвину точку X в другое положение так, чтобы XY стал перпендикулярен к a, и при этом я сделаю отрезок XY короче (в силу § 3). Это рассуждение, очевидно, в такой же мере, как к X, применимо и к Y; и поэтому мы видим: длина отрезка XY не может быть минимальной, если этот отрезок не перпендикулярен и к a, и к b. Если кратчайшее расстояние существует, то оно должно достигаться для общего перпендикуляра к двум данным прямым.

Мы не должны ничего брать на веру. На самом деле мы можем с первого взгляда видеть, что общий перпендикуляр действительно дает кратчайшее расстояние. Будем считать, что на рис. 8.5 плоскость чертежа параллельна обеим данным прямым a и b (a выше, b ниже). Любую точку или прямую в пространстве мы можем рассматривать как представленную на рис. 8.5 ее ортогональной проекцией. Истинная длина отрезка XY равна гипотенузе прямоугольного треугольника, один катет которого есть ортогональная проекция отрезка XY, изображенная на рис. 8.5, а второй катет есть кратчайшее расстояние между двумя параллельными плоскостями, одна из которых проходит через a„ другая через b, причем обе они параллельны плоскости чертежа, к которой второй катет перпендикулярен. Поэтому чем короче проекция отрезка XY, изображенная на рис. 8.5, тем короче сам отрезок XY. Проекция отрезка XY сводится к точке, ее длина равна нулю, и, таким образом, длина XY минимальна в том и только в том случае, если отрезок XY перпендикулярен к плоскости чертежа и, значит, к обеим прямым a и b.

148

Итак, мы прямо подтвердили то, что ранее обнаружили с помощью другого метода.

(2) Найти максимум площади многоугольника, вписанного в данную окружность и имеющего данное число сторон.

Дана окружность. На этой окружности мы должны так выбрать n вершин U, …, W, X, Y и Z многоугольника, чтобы площадь стала максимальной. В точности, как и в предыдущей задаче (1), главная трудность, по-видимому, состоит в том, что имеется много переменных (вершины U, …, W, X, Y и Z). Нам следует, пожалуй, испробовать метод, работавший в предыдущей задаче. В чем суть этого метода?

Р и с. 8.6. Треугольник максимальной площади.

Рассмотрим задачу как почти решенную. Представим себе, что мы уже получили искомое положение всех вершин, за исключением одной, скажем X. Другие n — 1 точек, U, …, W, X, Y и Z, уже фиксированы, каждая в том положении, в котором она должна находиться, но нужно еще так выбрать X, чтобы площадь стала максимальной. Вся площадь, однако, состоит из двух частей: многоугольника U…WYZ с n — 1 фиксированной вершиной, который от X не зависит, и треугольника WXY, зависящего от X. Сосредоточим свое внимание на этом треугольнике, площадь которого, когда вся площадь становится максимальной, также должна стать максимальной; см. рис. 8.6. Основание WY треугольника WXY фиксировано. Если вершина X движется по параллели к основанию WY; то площадь остается постоянной; такие параллели к WY являются линиями уровня. Выберем касательную линию уровня: касательную к окружности, параллельную основанию WY. Ее точка касания, очевидно, есть положение вершины Х, обращающее площадь треугольника WXY в максимум. Когда Х займет это положение, треугольник станет равнобедренным, WX = XY. Если площадь многоугольника максимальна, то две соседние стороны должны быть равны. Но то же самое рассуждение применимо и к любой паре соседних сторон: когда достигается максимум площади, все стороны должны быть равны, и, таким образом, вписанный многоугольник максимальной площади должен быть правильным.

5. Схема частного изменения. Сравнивая два примера, рассмотренные в предыдущем параграфе (§ 4), мы легко обнаруживаем некоторые общие черты и общую схему решения. В обеих задачах мы разыскивали экстремум (минимум или максимум) величины, зависящей от нескольких переменных элементов. В обоих решениях мы на время фиксировали все первоначально переменные элементы,

149

за исключением одного, и изучали эффект от изменения этого единственного элемента Одновременное изменение всех переменных элементов, или полное изменение не так легко обозреть. Нам удалось решить наши задачи, изучая частное изменение, когда изменяется только один элемент, а другие фиксированы. Вот принцип, лежащий в основе нашего образа действий: функция f нескольких переменных не может достигать максимума по отношению к совокупности всех своих переменных, если она не достигает максимума по отношению к каждой переменной в отдельности.

Это утверждение является весьма общим, хотя в одном отношении и излишне ограничительным; оно слишком тесно примыкает к предыдущим примерам, в которых в каждый данный момент времени мы изменяли лишь один элемент. Однако можно себе представить, что в других примерах может оказаться выгодным изменять одновременно ровно два элемента и фиксировать другие или, допустим, ровно три и т. д. В таких случаях еще естественно было бы говорить о «частном изменении». Общая идея выступает теперь довольно ясно, и после еще одного примера читатель самостоятельно сумеет довести ее до полной ясности.

Отрезок длины l делится на n частей. Найти максимум произведения длин этих n частей.

Пусть x₁, x₂, …, x_n — длины этих n частей; x₁, x₂, …, x_n — положительные числа с данной суммой:

x₁ + x₂ + … + x_n = l

Требуется сделать максимальным произведение x₁x₂…x_n.

Исследуем сначала простейший частный случай: дана сумма x₁ + x₂ двух положительных величин; найти максимум их произведения x₁x₂. Мы можем интерпретировать x₁ и x₂ как соседние стороны прямоугольника и высказать задачу в следующей более привлекательной форме: дан периметр прямоугольника; найти максимум его площади. В самом деле, сумма двух только что упомянутых сторон задана:

Сразу возникает догадка: площадь становится максимальной, когда прямоугольник превращается в квадрат. Эту догадку легко проверить. Каждая сторона квадрата с периметром L равна

Мы должны убедиться в том, что площадь квадрата больше, чем площадь прямоугольника, или, что то же самое, что их разность

150

положительна. Так ли это? Немного алгебры, и мы получаем

Эта формула показывает все с одного взгляда. Правая часть положительна, если x₁ не равно x₂ и если прямоугольник не является квадратом.

Короче говоря, площадь прямоугольника с данным периметром становится максимальной, когда прямоугольник есть квадрат; произведение двух положительных величин с данной суммой становится максимальным, когда эти две величины равны.

Попытаемся воспользоваться частным случаем, решение которого только что найдено, как ступенью для решения общей задачи. Рассмотрим задачу как почти решенную. Представим себе, что мы уже получили искомые значения всех частей, за исключением первых двух, x₁ и x₂. Таким образом, мы считаем x₁ и x₂ переменными, а x₃, x₄ …, x_n постоянными. Сумма двух переменных частей постоянна,

x₁ + x₂ = l — x₃ — x₄ — … — x_n._.

Далее, произведение всех частей

x₁x₂(x₃x₄ … x_n)

не может стать максимальным, если не станет максимальным и произведение x₁x₂ первых двух частей. Это, однако, требует, чтобы x₁ = x₂. Но нет причины, почему бы любая другая пара частей должна была бы вести себя иначе. Искомый максимум произведения не может достигаться, если все величины, имеющие данную сумму, не равны. Мы процитируем Колина Маклорена (1698 — 1746), которому принадлежит предыдущее рассуждение: «Если Линия AB разделена на любое Число Частей AC, CD, DE, EB, то Произведение всех этих Частей, умноженных одна на другую, будет Максимальным, когда эти Части равны между собой»[42].

Читатель может многому научиться, разбирая приведенное доказательство. Вполне ли оно удовлетворительно?

6. Теорема о среднем арифметическом и средним геометрическом ее первые следствия. Рассмотрим результат предыдущего параграфа: Пусть

x₁ + x₂ + x₃ … + x_n = l;

тогда

если не выполняется условие x₁ = x₂ = x₃ =… = x_n = l/n. Исклю-

151

чая l, можем сформулировать этот результат в форме:

или

если не все положительные величины x₁, x₂, …, x_n равны; если же эти величины равны, то неравенство становится равенством. Левая часть написанного выше неравенства называется средним геометрическим, а правая — средним арифметическим величин x₁, x₂, …, x_n. Только что сформулированную теорему иногда называют «теоремой о среднем арифметическом и среднем геометрическом», или, короче, «теоремой о средних».

Теорема о средних интересна и важна во многих отношениях. Стоит упомянуть, что она может быть высказана в двух различных формах:

Произведение n положительных величин с данной суммой становится максимальным, когда все эти величины равны.

Сумма n положительных величин с данным произведением становится минимальной, когда все эти величины равны.

В первой формулировке речь идет о максимуме, во второй — о соответствующем минимуме. Вывод предыдущего параграфа относится к первой формулировке. Систематически изменяя этот вывод, мы могли бы прийти ко второй формулировке. Проще, однако, заметить, что неравенство между средними одновременно дает обе формулировки: чтобы получить ту или другую, мы должны рассматривать как данную ту или другую часть неравенства. Мы можем называть эти две (по существу равносильные) формулировки сопряженными формулировками.

Теорема о средних позволяет решать многие геометрические задачи на максимум и минимум. Мы рассмотрим здесь только один пример (несколько других можно найти в конце этой главы).

Дана площадь поверхности ящика; найти максимум его объема.

Я пользуюсь словом «ящик» вместо слов «прямоугольный параллелепипед», потому что слово «ящик» достаточно выразительно и значительно короче, чем официальный термин.

Решение легко предвидеть, и раз уж мы его предвидим, оно легко сводится к теореме о средних. Пусть

a, b, c — длины трех ребер ящика, выходящих из одной и той же вершины,

S — площадь поверхности,

V — объем.

Очевидно,

S = 2(ab + ac + bc), V = abc.

152

Замечая, что сумма трех величин ab, ac и bc равна S/2, а их произведение равно V², мы, естественно, вспоминаем теорему о средних, которая дает

если не выполняются равенства

ab = ac = bc,

или, что то же самое,

a = b = c

Иначе говоря,

V < (S/6)^3/2,

если ящик не является кубом, когда осуществляется равенство. Мы можем выразить результат в двух различных (хотя по существу эквивалентных) формах:

Из всех ящиков с данной площадью поверхности куб имеет наибольший объем.

Из всех ящиков с данным объемом куб имеет наименьшую площадь поверхности.

Как и выше, мы можем две эти формулировки называть сопряженными формулировками. Как и выше, в одной из двух сопряженных формулировок речь идет о максимуме, а в другой — о минимуме.

Приведенное приложение теоремы о средних обладает и своими достоинствами. Мы можем его рассматривать как схему и собирать случаи, к которым теорема о средних может быть подобным же образом применена.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ VIII

Первая часть

1. Наименьшае и наибольшие расстояния в плоской геометрии. Найдите наименьшее расстояние между (1) двумя точками, (2) точкой и прямой, (3) двумя параллельными прямыми.

Найдите наименьшее и наибольшее расстояния между (4) точкой и окружностью, (5) прямой и окружностью, (6) двумя окружностями.

Решение во всех случаях очевидно. Вспомните, по крайней мере в нескольких случаях, элементарное доказательство.

2. Наименьшие и наибольшие расстояния в пространственной геометрии. Найдите наименьшее расстояние между (1) двумя точками, (2) точкой и плоскостью, (3) двумя параллельными плоскостями, (4) точкой и прямой, (5) плоскостью и параллельной ей прямой, (6) двумя скрещивающимися прямыми.

Найдите наименьшее и наибольшее расстояния между (7) точкой и сферой, (8) плоскостью и сферой, (9) прямой и сферой, (10) двумя сферами,

3. Линии уровня на плоскости. Рассмотрите расстояние переменной точки от данной (1) точки, (2) прямой, (3) окружности. Каковы линии уровня?

153

4. Поверхности уровня в пространстве. Рассмотрите расстояние переменной точки от данной (1) точки, (2) плоскости, (3) прямой, (4) сферы. Каковы поверхности уровня?

5. Ответьте на вопросы примера 1, пользуясь линиями уровня.

6. Ответьте на вопросы примера 2, пользуясь поверхностями уровня,

7. Даны две стороны треугольника. Найдите максимум площади, пользуясь линиями уровня.

8. Даны сторона и периметр треугольника. Найдите максимум площади, пользуясь линиями уровня,

9. Дана площадь прямоугольника. Найдите минимум периметра, пользуясь линиями уровня. [Пусть (0, 0), (x, 0), (0, y), (x, y) — четыре вершины прямоугольника в прямоугольной системе координат; воспользуйтесь аналитической геометрией.]

10. Исследуйте следующее утверждение: «Кратчайшее расстояние от данной точки до данной кривой есть длина перпендикуляра, проведенного из данной точки к данной кривой».

11. Принцип пересекающей линии уровня. Рассмотрим функцию f переменной точки на плоскости, максимум и минимум функции f на предписанном пути и линию уровня функции f, разделяющую две области плоскости; в одной из этих областей f принимает бо́льшие, а в другой — меньшие, чем на самой линии уровня, значения,

Если предписанный путь пересекает эту линию уровня, то в точке пересечения не достигается ни максимум, ни минимум функции 7.

Рис. 8.7. Линии уровня на контурной карте.

12. Контурная карта на рис, 8.7 изображает вершину В и перевал (или седловую точку с горизонтальной касательной плоскостью) П. Путешествуя по такой стране, достигните ли вы непременно наиболее высокой точки своего пути в точке, где этот путь касается линии уровня?

13. Пусть A и B — две данные точки, а X — переменная точка на плоскости. Стягиваемый отрезком AB угол в точке X [∠ AAB), который может принимать любое значение между 0° и 180° (включая границы), является функцией переменной точки X.

(1) Дайте полное описание линий уровня.

(2) Какая из двух различных линий уровня соответствует большему значению угла?

154

Вы можете пользоваться рис. 8.1 и 8.3, но должны ясно понять, что теперь вы можете смотреть на отрезок АВ с обеих сторон.

14. Рассмотрите рис. 8,1, 8.2, 8.3, возьмите ∠ AXB, как в примере 13 и найдите его минимум на l. Соответствует ли результат принципу примера 11?

15. Дан объем ящика (прямоугольного параллелепипеда). Пользуясь частным изменением. найдите минимум площади его поверхности.

16. Какой из всех треугольников с данным периметром имеет наибольшую площадь? [Пример 8.]

17. Какой из всех тетраэдров, вписанных в данную сферу, имеет наибольший объем! [Знаете ли вы какую-нибудь задачу, родственную этой?]

18. Даны длины a, b и c трех ребер тетраэдра, проведенных из одной и той же вершины. Найдите максимум объема тетраэдра. [Знаете ли вы какую-нибудь аналогичную задачу?)

19. Найдите кратчайшее расстояние между сферой и цилиндром. [Под цилиндром понимается бесконечный цилиндр вращения.)

20. Найдите кратчайшее расстояние между двумя цилиндрами со скрещивающимися осями.

21. Исследуйте утверждение: «Кратчайшее расстояние между двумя данными поверхностями есть длина общего перпендикуляра к обеим поверхностям»

22. Принцип частного изменения. Функция f (X, Y, Z, …) нескольких переменных X, Y, Z, … достигает своего максимума при X = A, Y = B, Z = C, … Тогда функция f (X, B, C, ...) одной переменной X достигает своего максимума при X = A, и функция f (X, Y, C, …) двух переменных X и Y, достигает своего максимума при X = A, Y = B, и т. д.

Функция нескольких переменных не мажет достигать максимума по отношению ко всем ее переменным в совокупности, если она не достигает максимума по отношению к любому подмножеству переменных.

23. Существование экстремума. И принцип линии уровня, и принцип частного изменения обычно дают только «отрицательную информацию». Они прямо показывают, в каких точках рассматриваемая функция f не может достигать максимума, а мы должны отсюда заключить, где f может достигнуть максимума. То, что f где-нибудь должна достигать максимума, не может быть выведено из одних лишь этих принципов. Однако существование максимума иногда может быть выведено с помощью какого-нибудь видоизменения рассуждения. Кроме того, существование максимума часто может быть выведено из общих теорем о непрерывных функциях нескольких переменных[46]. Как бы то ни было, всякий раз, когда с интуитивной точки зрения существование максимума кажется очевидным, мы имеем достаточные основания надеяться, что для доказательства существования подойдет какой-нибудь специальный прием или какая-нибудь общая теорема[43].

24. Видоизменение схемы частного изменения: бесконечный процесс. Найдите максимум произведения xyz, если дано, что x + y + z =l.

Подразумевается, что x, y и z — положительные числа и что l задано. Эта задача является частным случаем задачи из § 5. Следуя методу, которым мы там воспользовались, зафиксируем одно из трех чисел x, y и z, а два других изменим так, чтобы они стали равными; при этом их произведение увеличится. Начнем с любой данной системы «x, y, z); производя указанное изменение, переходим к другой системе (x₁, y₁, z₁); затем переходим к новой системе (x₂, y₂, z₂), а от нее к (x₃, y₃, z₃) и т. д. Мы будем поочередно оставлять неизменным одно из наших трех чисел; сначала x, затем y, затем z, затем снова x, затем у, затем z, затем снова x и т. д. Итак, мы

155

полагаем

..........................

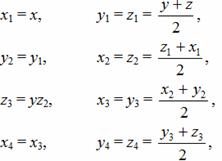
Каждый шаг не изменяет сумму, но увеличивает произведение:

x, + y + z = x₁ + y₁ + z ₁ = y₂ + x₂ + z₂ = …, xyz < x₁y₁z₁ < y₁x₁z₁

Допустим, что y ≠ z, x₁ ≠z₁. (Это не исключительный случай: в исключительном случае мы придем к нашему результату значительно легче.) Естественно ожидать, что когда n возрастает, три числа x_n, y_n и z_n будут все меньше и меньше отличаться друг от друга. Если мы сумеем доказать, что в конце концов

то немедленно сможем заключить, что

Мы получаем, таким образом, этот результат с большой затратой сил, но не предполагая заранее существования максимума.

25. Другое видоизменение схемы частного изменения: конечный процесс. Вновь рассмотрим пример 24, но воспользуемся теперь более сложным видоизменением метода § 5.

Пусть l = 3A; таким образом, A есть среднее арифметическое чисел x, y и z, и мы имеем

(x — A) + (y — A) + (z — A) = 0

Может случиться, что x = y = z. Если же это не так, то одна из разностей в левой части нашего равенства должна быть отрицательной, а другая положительной. Выберем обозначения так, чтобы

y < A < z.

Перейдем от системы (xyz) к системе (x′y′z′), полагая

x′ = x, y′ = A, z′ = y + (z — A);

первую величину мы оставили неизменной. Тогда

x + y + z = x′ + y′ + z′

и

y′z′ — yz = A(y + z — A) — yz = (A — y)(z — A) > 0,

так что

xyz < x'y'z'.

Может случиться, что x′ = y′ = z′. Если это не так, то перейдем от (x', y', z') к (x″, y″, z″), полагая

156

что дает

x″ = y″ = z″ = A,

и снова (как мы знаем из § 5) произведение увеличивается, так что

Мы доказали желаемый результат без предположения о существовании максимума и без рассмотрения пределов.

С помощью подходящего расширения этого метода докажите теорему о средних (§ 6) в общем виде для n величин.

26. Графическое сравнение. Пусть P — точка, лежащая внутри равностороннего треугольника с высотой l, а x, y и z — расстояния точки P от трех сторон треугольника[44]; см. рис. 8.8. Тогда

x + y + z = l.

(Почему?) Числа x, y и z являются треугольными координатами точки Р. Любую систему трех положительных чисел x, y и z с суммой l можно интерпретировать как треугольные координаты однозначно определенной точки внутри треугольника.

Рис. 8.8. Треугольные координаты.	Рис. 8.9. Последовательные шаги, приближающие центр.

Последовательность

(x, y, z), (x₁, y₁, z₁) (x₂, y₂, z₂), …,

рассмотренная в примере 24, изображается на рис, 8,9 последовательностью точек. Отрезки, соединяющие соседние точки, поочередно параллельны различным сторонам треугольника: первой, второй, третьей, затем снова первой стороне и т. д.; каждый отрезок оканчивается на высоте треугольника. (Почему?) Процесс примера 25 изображается тремя точками и двумя отрезками. (Как?)

27. Пересмотрите рассуждение § 4 (2) и видоизмените его, взяв в качестве модели сначала пример 24, а затем пример 25.

28. Необходимое условие для того, чтобы функция f(x, y, z) имела в точке (a, b, c) максимальное или минимальное значение, состоит в том, что при x = a, y =b, z = c частные производные

обращаются в нуль.

Обычное доказательство этой теоремы служит примером для одной ив наших схем. Какой?

157

29. Установите хорошо известное (выражающееся через частные производные) необходимое условие для максимального или минимального значения функции f (x, y) при краевом (!или дополнительном) условии, что x и y связаны уравнением g (x, y) = 0. Объясните связь со схемой касательной линии уровня.

30. Вновь исследуйте случаи, упомянутые в примере 12 в свете условия примера 29. Есть ли какое-нибудь противоречие?[45]

31. Установите хорошо известное необходимое условие для максимального или минимального значения функции f (x, y, z) при краевом условии g (x, y, z). Объясните связь со схемой касательной поверхности уровня.

32. Установите хорошо известное необходимое условие для максимального или минимального значения функции f (x, y, z) при двух одновременно выполняющихся краевых условиях g (x, y, z) = 0 и g (x, y, z) = h. Объясните связь со схемой касательной поверхности уровня.

Вторая часть

Употребляемые ниже терминология и обозначения объяснены в примере 33, который следует прочитать вначале[46].

33. Многоугольники и многогранники. Площадь и периметр. Объем и поверхность. Для многоугольников мы по большей части будем пользоваться следующими обозначениями:

A — площадь и

L — длина периметра.

Для многогранников мы примем:

V — объем и

S — площадь поверхности.

Мы будем рассматривать задачи на максимум и минимум, относящиеся к A и L или к V и S. Такие задачи были известны древним грекам[47]. Мы рассмотрим, главным образом, задачи, которыми занимались Симон Люилье и Якоб Штейнер[48]. При решении большинства нижеследующих задач окажутся полезными элементарные алгебраические неравенства, особенно теорема о средних (§ 6).

Эти задачи по большей части относятся только к простейшим многоугольникам (треугольникам и четырехугольникам) и к простейшим многогранникам (призмам и пирамидам), Нам нужно усвоить несколько менее обычных терминов.

Две пирамиды, расположенные по разные стороны от их общего основания, вместе образуют двойную пирамиду. Если основание имеет n сторон, то двойная пирамида имеет 2 n граней, n +2 вершины и Зn ребер. Основание не является гранью двойной пирамиды.

Если все боковые грани призмы перпендикулярны основанию, то мы называем эту призму прямой призмой.

Если основание пирамиды описано около круга и высота пересекается с основанием в центре этого круга, то мы называем эту пирамиду прямой пирамидой.

Если две пирамиды, образующие двойную пирамиду, являются прямыми пирамидами и симметричны относительно их общего основания, то мы называем эту двойную пирамиду прямой двойной пирамидой.

Если призма, пирамида или двойная пирамида не являются «прямыми», та мы называем их «наклонными». Среди пяти правильных многогранников имеется ровно одна призма, ровно одна пирамида и ровно одна двойная

158

пирамида: соответственно куб, тетраэдр и октаэдр. Каждый из этих трех многогранников является «прямым» многогранником своего типа.

Мы будем также рассматривать цилиндры, конусы и двойные конусы; если нет оговорки о противном, предполагается, что их основания — круги.

34. Прямая призма с квадратным основанием. Из всех прямых призм с квадратным основанием, имеющих данный объем, наименьшую поверхность имеет куб.

Докажите этот частный случай уже доказанной теоремы (§ 6, пример 15), пользуясь теоремой о средних.

Вы можете соблазниться поступить следующим образом. Пусть V, S, x и y, соответственно, обозначают объем, площадь поверхности, сторону основания и высоту призмы. Тогда

V = x²y, S = 2x² + 4xy.

Применяя теорему о средних, получаем

(S/2)² = [(2x² + 4 xy)/2]³ ≥ 2x²·4xy =8x³y.

Но правая часть не имеет к V = x²y никакого отношения; такое неравенство бесполезно — теорема о средних кажется неприменимой.

Это было, однако, опрометчивое, неразумное, непрофессиональное применение этой теоремы. Сделайте еще одну попытку. [В чем состоит желаемое заключение?)

35. Прямой цилиндр. Заметьте, что из всех призм, рассмотренных в примере 34, только куб можно описать около шара, и докажите: Из всех прямых цилиндров, имеющих данный объем, наименьшую поверхность имеет цилиндр, описанный около шара. [В чем состоит желаемое заключение?]

36. Произвольная прямая призма. Даны объем прямой призмы и форма [но не размеры) ее основания. Когда площадь поверхности минимальна, какую ее долю составляет площадь основания? [Знаете ли вы какую-нибудь задачу, связанную с этой?]

37. Прямая двойная пирамида с квадратным основанием. Докажите: Из всех прямых двойных пирамид с квадратным основанием, имеющих данный объем, наименьшую поверхность имеет правильный октаэдр[47].

38. Прямой двойной конус. Заметьте, что вписанный шар касается каждой грани правильного октаэдра в ее центре, который делит высоту грани в отношении 1: 2, и докажите: Из всех прямых двойных конусов, имеющих данный объем, минимум поверхности достигается двойным конусом, образующие которого делятся точками касания со вписанным шаром в отношении 1 : 2[48].

39. Произвольная прямая двойная пирамида. Даны объем прямой двойной пирамиды и форма [но не размеры) ее основания. Когда площадь поверхности минимальна, какую ее долю составляет площадь основания?[49]

40. Дана площадь треугольника. Найдите минимум его периметра. [Могли ли бы вы предсказать результат? Если вы хотите попытаться применить теорему о средних, то вам может понадобиться выражение площади через стороны.]

41. Дана площадь четырехугольника. Найдите минимум его периметра. [Могли ли бы вы предсказать результат? Обозначьте буквами a, b, c и d стороны четырехугольника, буквой ε — сумму двух противоположных углов и выразите площадь A через a, b, c, d и ε. Это обобщение задачи, решение которой дается формулой Герона.]

42. Прямая и наклонная призмы имеют одинаковый объем и одно и то же основание. Тогда прямая призма имеет меньшую поверхность.

Прямая и наклонная пирамиды имеют одинаковый объем и одно и то же основание. Тогда прямая пирамида имеет меньшую поверхность.

Прямая и наклонная двойные пирамиды имеют одинаковый объем и одно и то же основание. Тогда прямая двойная пирамида имеет меньшую поверхность.

159

Во всех трех утверждениях основания двух сравниваемых тел совпадают и по форме, и по величине. (Объемы, конечно, совпадают только по величине.)

Выберите из этих трех утверждений то, которое кажется вам наиболее доступным, и докажите его.

43. Приложение геометрии к алгебре. Докажите: Если u₁, u₂, … , u_n, v₁, v₂, …, v_n, — действительные числа, то

и равенство достигается в том и только в том случае, если

u₁ : v₁ = u₂ : v₂ = … = u_n : v_n

[Рассмотрите в прямоугольной системе координат n + 1 точку P₀, P₁, P₂ …, P_n, и длину ломаной линии P₀P₁P₂…P_n,]

44. Докажите неравенство примера 43 независимо от геометрических рассмотрений. [В геометрическом доказательстве этого неравенства ведущим частным случаем является n = 2.]

45. Приложение алгебры к геометрии. Докажите: Из всех треугольников с данным основанием и площадью наименьший периметр имеет равнобедренный треугольник. [Пример 43.)

46. Пусть V, S, A и L, соответственно, обозначают объем, площадь поверхности, площадь основания и периметр основания пирамиды P. Пусть V₀, S₀, A₀ и L₀ — соответствующие величины, связанные с другой пирамидой P₀,. Приняв, что

V = V₀, A = A₀, L ≥ L ₀

и что P₀ — прямая пирамида, докажите, что

S ≥ S ₀.

Равенство достигается в том и только в том случае, если L = L ₀ и P также является прямой пирамидой. [Пример 43.[

47. Пусть V, S, A и L, соответственно, обозначают объем, площадь поверхности, площадь основания и периметр основания двойной пирамиды D. Пусть V, S, A и L, — соответствующие величины, связанные с другой двойной пирамидой D₀,. Приняв, что

V = V₀, A = A₀, L ≥ L ₀

и что О,— прямая двойная пирамида, докажите, что

S ≥ S ₀.

Равенство достигается в том и только в том случае, если L = L ₀ и D также является прямой двойной пирамидой. [Примеры 45, 46.)

48. Докажите: Из всех четырехгранных призм данного объема наименьшую поверхность имеет куб. [Сравните с примером 34; какое утверждение сильнее?)

49. Докажите: Из всех восьмигранных двойных пирамид данного объема наименьшую поверхность имеет правильный октаэдр. [Сравните с примером 37; какое утверждение сильнее?)

50. Докажите: Из всех трехгранных пирамид данного объема[50] наименьшую поверхность имеет правильный тетраэдр.

51. Прямая пирамида с квадратным основанием. Докажите: Из всех прямых пирамид с квадратным основанием, имеющих данный объем, наименьшую поверхность имеет пирамида, у которой основание составляет 1/4 полной поверхности[51].

160

52. Прямой конус. Из всех прямых конусов, имеющих данный объем, наименьшую поверхность имеет конус, у которого основание составляет 1/4 полной поверхности[52].

53. Произвольная прямая пирамида. Даны объем прямой пирамиды и форма (но не размеры) ее основания. Когда площадь поверхности минимальна, какую ее долю составляет площадь основания?[53] [Знаете ли вы какой-нибудь частный случай?]

54. Просматривая вновь наши различные примеры, относящиеся к призмам, пирамидам и двойным пирамидам, подметьте их взаимные связи и расположите их в виде таблицы так, чтобы стала заметна аналогия результатов. Укажите пробелы, которые вы надеетесь заполнить дальнейшими результатами.

55. Ящик без крышки. Дана сумма S₅ площадей пяти граней ящика. Найдите максимум объема V. [Знаете ли вы какую-нибудь задачу, родственную этой? Могли бы вы воспользоваться результатом или методом?]

56. Корыто. Дана сумма S₄ площадей четырех граней прямой трехгранной призмы; отброшена боковая грань. Найдите максимум объема V.

57. Обломок. Дана сумма S₃ площадей трех попарно соседних граней (т. е. двух боковых граней и одного основания) прямой призмы с треугольным основанием. Покажите, что когда объем V достигает своего максимума, эти три грани имеют равную площадь и попарно перпендикулярны. [Обломок чего?[54]]

58. Дана площадь сектора круга. Найдите значение угла в центре, при котором периметр является наименьшим.

59. Даны площадь и угол треугольника. Найдите минимум (1) суммы двух сторон, заключающих данный угол, (2) стороны, противолежащей данному углу, (3) всего периметра.

60. Даны угол и точка в плоскости угла, лежащая внутри угла. Переменная прямая, проходящая через данную точку, отсекает от угла треугольник, Найдите минимум площади этого треугольника.

61. Дана сумма E длин 12 ребер ящика. Найдите максимум (1) его объема V, (2) его поверхности S.

62. Почтовая задача. Найдите максимум объема ящика, если дано, что его длина и обхват вместе не превышают l сантиметров.

63. Задача Кеплера. Дано расстояние d от середины образующей прямого цилиндра до наиболее далекой точки цилиндра. Найдите максимум объема этого цилиндра.

IХ. ФИЗИЧЕСКАЯ МАТЕМАТИКА

Физика не талька дает нам [математикам] повод к решению проблем; она еще помогает нам найти к этому средства. Это происходит двояким путем. Во-первых, она дает нам предчувствие решения; во-вторых, подсказывает нам ход[55] рассуждений. — Анри Пуанкаре[49]

1. Оптическая интерпретация. Математические задачи часто внушаются природой или, вернее, нашей интерпретацией природы, физическими науками. Решение математической задачи также может внушаться природой; физика обеспечивает нас ключами, которыми, будучи предоставлены самим себе, мы имели бы очень мало шансов себя обеспечить. Наша картина была бы слишком узкой, если бы мы не рассмотрели математические задачи, подсказанные физическим исследованием и решенные с помощью физической интерпретации. Вот первая, очень простая задача этого рода.

(1) Природа подсказывает задачу. Прямая есть кратчайший путь между двумя данными точками. Свет, распространяясь в воздухе от одной точки к другой, выбирает этот кратчайший путь; так, по крайней мере, показывает, по-видимому, наш повседневный опыт[56]. Но что происходит, когда свет распространяется от одной точки к другой не прямо, а подвергаясь отражению от поставленного на его пути зеркала. Выберет ли свет снова кратчайший путь? Каков кратчайший путь при этих обстоятельствах? Изучение распространения света приводит нас к следующей чисто геометрической задаче:

Даны две точки и прямая, лежащие в одной плоскости, причем обе точки находятся по одну сторону от прямой. На данной прямой найти такую точку, чтобы сумма ее расстояний от двух данных точек была наименьшей.

Пусть (см. рис. 9.1)

A и B — две данные точки,

l — данная прямая,

X — переменная точка прямой l.

Рассмотрим сумму AX + XB двух расстояний, или, что то же самое, длину пути, ведущего от A к X и от X к B. Требуется найти такое положение точки Х на данной прямой l, для которого длина этого пути достигает своего минимума.

162

Мы встречались ранее (§ 8.2, рис. 8.1, 8.2, 8.3) с очень похожей задачей. Действительно, обе задачи имеют в точности одни и те же данные и даже неизвестное в обоих случаях одинаковой природы. Здесь, как и там, мы разыскиваем положение точки на данной прямой, для которого достигается некоторый экстремум. Наши две задачи отличаются только природой этого экстремума. Здесь мы разыскиваем минимум суммы длин двух отрезков, а там мы разыскивали максимум угла, образованного этими двумя отрезками.

Тем не менее эти две задачи так тесно связаны, что естественно испытать тот же метод. При решении задачи из § 8.2 мы пользовались линиями уровня; воспользуемся ими снова.

Рис. 9.2. Касательная линия уровня.	Рис. 9.2. Какой путь самый короткий?

Рассмотрим точку X, которая не обязана находиться на предписанном пути, но может свободно двигаться по всей плоскости. Как может двигаться точка X, если величина AX + XB (минимум которой мы хотим найти) имеет постоянное значение? По эллипсу с фокусами в A и B. Следовательно, линии уровня — это «конфокальные» эллипсы, т. е. эллипсы с одними и теми же фокусами (данными точками A и B). Искомый минимум достигается в точке касания предписанного пути l с эллипсом, фокусами которого являются данные точки A и B (см. рис 9.2).

(2) Природа подсказывает решение. Мы, действительно, нашли решение. Однако если мы не знаем некоторых геометрических свойств эллипса, наше решение не приносит большой пользы. Начнем снова и постараемся найти решение, дающее больше информации.

Ясно представим себе физическую обстановку, из которой возникает наша задача. Точка A есть источник света, точка B — глаз наблюдателя, а l указывает положение отражающей плоской поверхности; мы можем думать о горизонтальной поверхности тихого пруда (которая перпендикулярна плоскости рис. 9.1 и пересекает ее по прямой l). Ломаная AXB, если точка X выбрана правильно, представляет путь света. Мы довольно хорошо по опыту знаем этот путь. Мы подозреваем, что длина ломаной AXB, когда она представляет действительный путь отражаемого света, является наименьшей.

163

Ваш глаз находится в точке B, и вы смотрите вниз на отражающий пруд, наблюдая в нем изображение точки A. Луч света, который вы воспринимаете, приходит не прямо от объекта A, но кажется приходящим из точки, находящейся под поверхностью пруда. Из какой точки? Из точки A*, — зеркального отражения A, — симметричной с A относительно прямой l.

Введите точку A*, подсказанную вашим физическим опытом, в чертеж! Эта точка A* изменяет облик задачи. Мы видим множество новых связей (рис. 9.3). Давайте, приведем их в порядок и побыстрее используем. Очевидно,

AX = A*X.

(AX есть зеркальное отражение отрезка AX. Вы можете также опираться на равенство треугольников ΔACX, Δ A*CX; прямая l есть перпендикуляр, делящий отрезок AA* пополам). Следовательно,

AX + XB = A*X + XB

Обе части этого равенства становятся минимальными при одном и том же положении точки x. Но правая часть, очевидно, является минимальной, когда A*, X и B лежат на одной и той же прямой. Прямая линия — кратчайшая.

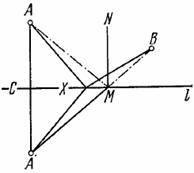
Рис. 9.3. Решение, дающее больше информации.

Это — решение (см. рис. 9.3). Точка M, положение минимума точки X, получается как пересечение прямой l и прямой, соединяющей A* и B. Очевидно, AM и MB образуют с l одинаковые углы. Вводя прямую MN, нормаль к l (параллель к A*A), видим, что

∠ AMN = ∠ BMN.

Кратчайший путь характеризуется равенством этих двух углов. Однако в точности то же самое равенство

угол падения = углу отражения

характеризует, как мы знаем по опыту, действительный путь света. Следовательно, в самом деле отражаемый луч света выбирает кратчайший возможный путь между объектом и глазом. Это открытие принадлежит Герону Александрийскому.

(3) Сравнение двух решений. Часто бывает полезно вновь просмотреть законченное решение. В настоящем случае это вдвойне полезно, так как мы имеем два решения (1) и (2), которые мы можем сравнить между собой. Оба метода решения задачи (рис. 9.2 и 9.3) должны давать один и тот же результат (представьте себе, что две

164

фигуры изложены одни на другую). Мы можем получить точку M, решение нашей задачи на минимум, с помощью эллипса, касательного к l, или же с помощью двух лучей, одинаково наклоненных к l. Однако, каким бы ни было относительное положение данных (точек A и B и прямой l), эти два построения должны находиться в согласии. Согласие этих двух построений влечет за собой геометрическое свойство эллипса:

Две прямые, соединяющие два фокуса эллипса с произвольной точкой периферии эллипса, одинаково наклонены к касательной к эллипсу в точке их пересечения.

Если мы представим себе эллипс как зеркало и примем во внимание закон отражения (который мы только что рассмотрели), то сможем сформулировать это геометрическое свойство иначе, в наглядной оптической интерпретации: Любой луч света, приходящий из фокуса эллиптического зеркала, отражается в другой фокус.

(4) Приложение. Открытие Герона, несмотря на свою простоту, заслуживает места в истории науки. Это — первый пример применения принципа минимума при описании физических явлений. Это — поучительный пример взаимосвязи между математической и физической теорией. После Герона были открыты значительно более общие принципы минимума и взаимосвязи между математической и физической теориями чрезвычайно расширились, но первые и простейшие примеры в некоторых отношениях производят наиболее глубокое впечатление.

Просматривая удачное решение (2), такое эффектное, мы должны спросить: Можно ли им воспользоваться? Можно ли воспользоваться результатом? Можно ли воспользоваться методом? В действительности существует несколько возможностей. Мы могли бы исследовать отражение светя в кривом зеркале, или последовательные отражения в серии плоских зеркал, или сочетать этот результат с методами, которые мы изучили раньше и т. д.

Рассмотрим здесь еще только один пример, задачу о «транспортном центре». Три города намереваются построить три дороги к общему транспортному центру, который должен быть выбран так, чтобы полная стоимость постройки дорог были наименьшей. Если мы все это предельным образом упростим, то получим следующую чисто геометрическую задачу: Даны три точки. Найти четвертую точку так, чтобы сумма ее расстояний от этих трех точек была наименьшей.

Пусть A, B и C обозначают три данные точки (города́), а Х— переменную точку на плоскости, определяемой точками A, B и C. Мы разыскиваем минимум суммы AX + BX + CX.

Эта задача кажется родственной задаче Герона. Нам нужно сблизить эти две задачи, установить между ними как можно более тесную связь. Если на момент мы фиксируем расстояние CX (скажем, будем считать его = r), то связь окажется действительно очень тесной: здесь,

165

как и там, нам нужно найти минимум суммы AX + BX расстояний одной переменной точки от двух фиксированных точек. Различие состоит в том, что здесь X обязана двигаться по окружности (радиуса r с центром в C), а там — по прямой. Предыдущая задача относилась к отражению в плоском зеркале, а эта задача относится к отражению в круглом зеркале.

Доверимся свету: у него хватит способностей найти кратчайший путь от A B. Но свет распространяется так, что угол падения равен углу отражения. Следовательно, в искомом положении минимума ∠ AXB должен делиться пополам прямой, проходящей через C и X (см. рис. 9.4). В силу принципа частного изменения и симметрии условий ∠ AXC и ∠ BXC также должны делиться пополам соответствующими прямыми. Три прямые, соединяющие X с A, B и C, разбивают плоскость на шесть углов, общей вершиной которых является X. Внимательно рассматривая пары вертикальных углов на рис. 9.5, легко видим, что все шесть углов равны и потому каждый из них равен 60°. Три дороги, расходящиеся из транспортного центра, одинаково наклонены одна к другой; угол между любыми двумя дорогами равен 120°.

Рис. 9.4. Транспортный центр и круглое зеркало.	Рис. 9.5. Транспортный центр.

(Если мы вспомним, что метод частного изменения, которым мы воспользовались, подчиняется некоторым ограничениям, то можем найти желательным критический пересмотр нашего решения.)

2. Механическая интерпретация. Математические задачи и их решения могут быть подсказаны любым сектором нашего опыта, оптическими, механическими или какими-нибудь другими явлениями. Посмотрим теперь, как простые механические принципы иногда помогают нам найти решение.

(1) Нить, оба конца которой закреплены, продета сквозь тяжелое кольцо. Найти положение равновесия.

166

Подразумевается, что нить является абсолютно гибкой и нерастяжимой, ее вес не учитывается, кольцо скользит по нити без трения и размеры кольца так малы, что его можно рассматривать как математическую точку.

Пусть A и B обозначают закрепленные концы нити, а X — любое положение кольца. На рис. 9.6 нить образует ломаную линию AXB.

Предлагаемая задача может быть решена двумя равными методами.

Во-первых, кольцо должно висеть как можно ниже. (Действительно, кольцо тяжелое; оно «хочет» как можно более приблизиться к земле, т. е. к центру Земли.) Обе части нерастяжимой нити AX и BX натянуты, и, таким образом, кольцо, скользя вдоль нити, описывает эллипс с фокусами A и B. Очевидно, положение равновесия есть наиболее низкая точка M этого эллипса, где касательная горизонтальна.

Рис. 9.6. Два условия равновесия.	Рис. 9.7. Транспортный центр с помощью механического устройства.

Во-вторых, силы, действующие на точку M нити, должны находиться в равновесии. На точку M действуют вес кольца и натяжения нити. Натяжения в обеих частях нити, MA и MB, равны и направлены вдоль нити соответственно к A и к B. Их равнодействующая делит ∠ AMB пополам и, будучи противоположна весу кольца, направлена вертикально.

Эти два решения должны, однако, находиться в согласии. Поэтому прямые MA и MB, одинаково наклоненные к вертикальной нормали эллипса, одинаково наклонены и к его горизонтальной касательной: две прямые, соединяющие два фокуса эллипса с произвольной точкой M периферии, одинаково наклонены к касательной в точке М. (Сохраняя длину отрезка АВ, но изменяя его угол наклона к горизонтали, мы можем поместить М в какое угодно положение на нижней половине эллипса)

Мы вывели уже известный результат [§ 1(3)] новым методом, который может допускать дальнейшие приложения,

167

(2) Кажется, мы обладаем излишком знаний. Не чересчур много учившись механике, мы, судя по всему, знаем ее достаточно не только для того, чтобы найти решение предложенной механической задачи, но и для того, чтобы найти два решения, основанные на двух равных принципах. Эти два решения, когда мы их сравнили, привели нас к интересному геометрическому факту. Не могли бы мы отвести какую-нибудь часть этого излишка механических знаний в другие каналы?

Если нам немного повезет, то мы сумеем представить себе механизм для решения задачи о транспортном центре, рассмотренной выше [§ 1(4)]. Три блока вращаются вокруг осей (гвоздей), закрепленных на вертикальной стене в точках A, B и C; см. рис. 9.7. Три нити, XAP, XBQ;) и XCR на рис. 9.7, проходят через блоки, соответственно, в A, B и C. В их общем конце X три нити соединены и к каждой из них в другом ее конце соответственно подвешен груз P, Q и R. Эти грузы P, Q и R равны. Наша задача состоит в том, чтобы найти положение равновесия.

Конечно, эта задача должна пониматься с обычными упрощениями: нити являются абсолютно гибкими и нерастяжимыми, трение, вес нитей и размеры блоков не учитываются (блоки рассматриваются как точки). Как и в «1), мы можем решить задачу двумя различными методами.

Во-первых, три груза должны совместно висеть как можно ниже, т. е. сумма их расстояний от данного горизонтального уровня [поверхности земли) должна быть минимальной (т. е. потенциальная энергия системы должна быть минимальной; вспомните, что три груза равны). Следовательно, сумма AP + BQ + CR должна быть максимальной. Поэтому, так как длина каждой нити постоянна, сумма AX + BX + CX должна быть минимальной, и, таким образом, наша задача оказалась тождественной с задачей о транспортном центре из § 1(4), рис. 9.4, 9.5.

Во-вторых, силы, действующие в точке X, должны находиться в равновесии. Три равных груда натягивают каждый свою нить с равной силой, и эти силы передаются блоками без потерь на трение, не уменьшаясь. Три равные силы, действуя на X соответственно по прямым XA, XB и XC, должны находиться в равновесии. Очевидно, в силу симметрии они должны быть одинаково наклонены одна к другой; угол между любыми двумя из трех нитей, соединяющихся в X, равен 120°. [Треугольник, обрадованный тремя нашими силами, является равносторонним, его внешние углы равны 120°.)

Это подтверждает решение из § 1(4). (С другой стороны, механическая интерпретация может подчеркнуть необходимость некоторых ограничений, относящихся к конфигурации трех точек A, B и C)

3. Новая интерпретация. Палка, наполовину погруженная в воду, кажется круто изогнутой. Отсюда мы заключаем, что свет, который как в воде, так и в воздухе распространяется прямолинейно, при

168

переходе из воды в воздух претерпевает резкое изменение направления. Это — явление преломления, явление, несомненно, более сложное и более трудное для понимания, чем отражение. Закон преломления после безуспешных усилий Кеплера и других был в конце концов открыт Снеллиусом (около 1621 г.) и опубликован Декартом. Еще позднее появился Ферма (1601—1665), который возвратился к цепи идей, начало которой положил Герон.

Свет, идущий от объекта A, находящегося под водой, к глазу B, находящемуся над водой, описывает ломаную линию с угловой точкой на поверхности, отделяющей воздух от воды, см. рис. 9.8. Однако кратчайший путь между A и B есть прямая, и, таким образом, свет при своем переходе из одной среды в другую не подчиняется принципу Герона. Это досадно; нам не хочется допустить, что простое правило, которое было справедливо в двух случаях (прямолинейное распространение и отражение), в третьем случае (преломление) не выполняется. Ферма пришло в голову, как достичь цели. Он был хорошо знаком с идеей о том, что свету для перехода от одной точки к другой нужно время, что он распространяется с некоторой (конечной) скоростью; действительно, Галилей предложил метод измерения скорости света Возможно, свет, распространяющийся с некоторой скоростью в воздухе, в воде распространяется с другой скоростью; такое различие в скорости могло бы, пожалуй, объяснить явление преломления.

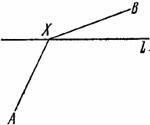
Рис. 9.8. Преломление.

Выбирая кратчайший путь, свет, поскольку он распространяется с постоянной скоростью, выбирает и наиболее быстрый путь. Если скорость зависит от среды, через которую он распространяется, то кратчайший путь уже не является непременно наиболее быстрым. Может быть, свет всегда выбирает наиболее быстрый путь, в том числе и при переходе из воды в воздух?

Эта цепь идей приводит к ясной задаче на минимум (см. рис. 9.8):

Даны две точки A и B, прямая l, отделяющая A от B, и две скорости u и v. Найти наименьшее время, необходимое для перехода от A к B; предполагается, что переход от A к l происходит со скоростью u, а от l к B со скоростью v.

Очевидно, быстрее всего двигаться по прямой от A до некоторой точки X прямой l и по некоторой другой прямой от X до B. Задача в сущности состоит в определении точки X. Далее, при равномерном движении время равняется расстоянию, деленному на скорость. Поэтому время, нужное для перехода от A до X и от X до X, равно

Эта сумма путем подходящего выбора точки X на прямой l должна

169

быть сделана минимальной. Мы должны найти X, если заданы A, B, u, v и l.

Решить эту задачу без помощи дифференциального исчисления не слишком легко. Ферма решил ее, придумав метод, который в конечном счете вел к дифференциальному исчислению. Мы лучше будем следовать указаниям, даваемым примерами предыдущего параграфа Если нам немного повезет, то мы сумеем представить себе механизм, который решит для нас предложенную задачу на минимум; см. рис. 9.9.

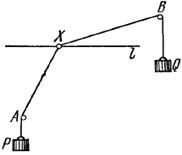
Рис. 9.9. Преломление с помощью механического устройства.

Кольцо X может скользить по закрепленному горизонтальному стержню l, который проходит сквозь кольцо. К кольцу X прикреплены две нити XAP и XBQ. Каждая из этих нитей проходит через блок (соответственно в A и в B), и в другом ее конце к ней подвешен груз (соответственно в P и в Q). Главное — выбрать грузы. Эти грузы не могут быть равны: если бы они были равны, то линия AXB в положении равновесия была бы прямой (по крайней мере это кажется правдоподобным), и, таким образом, она не годилась бы для изображения пути преломленного света Отложим выбор грузов, но введем подходящие обозначения. Обозначим через p груз в конце P первой нити и черед q — груз в конце Q второй нити. А теперь мы должны найти положение равновесия. (Мы принимаем обычные упрощения: стержень является абсолютно жестким, нити — абсолютно гибкими, но и нерастяжимыми; мы не учитываем трения, веса нитей и их сопротивления изгибу, размеров блоков и размеров кольца.) Как и в § 2, мы решаем нашу задачу двумя различными методами.

Во-первых, два груда должны совместно висеть как можно ниже (т. а потенциальная энергия системы должна быть минимальной). Отсюда следует, что сумма

AP·p + BQ·q

должна быть максимальной. Поэтому, так как длина каждой нити неизменна, сумма

AX·p + XB·q

должна быть минимальной.

Это очень близко к задаче Ферма, но не точно то же самое. Однако эти две задачи, оптическая и механическая, будут математически совпадать, если мы выберем

p = 1/u, q = 1/v.

170

Тогда задача о равновесии (рис. 9.9), в точности как и задача Ферма о наиболее быстром распространении, требует, чтобы сумма

была минимальной. Это мы нашли, рассматривая равновесие механической системы на рис. 9.9 с первой точки зрения.

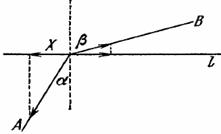
Рис. 9.10. Закон преломления.

Во-вторых, силы, действующие на точку X, должны находиться в равновесии. Натяжения от грузов передаются без потерь на трение в блоках, не уменьшаясь. К кольцу приложены две силы, соответственно величины ¹/_u и ¹/_v, причем каждая сила действует в направлении соответствующей нити. Эти силы не могут перемещать кольцо в вертикальном направлении, потому что стержень l, проходящий сквозь кольцо, абсолютно жесткий (вертикальная реакция стержня может иметь любую величину). Однако горизонтальные составляющие этих двух натяжений, имеющие противоположные направления, должны взаимно уничтожаться, должны быть равны по величине. Для того чтобы выразить это соотношение, введем углы α и β между проходящей через точку X вертикалью и двумя нитями; см. рис. 9.10. Равенство горизонтальных составляющих выражается так:

или

Это — условие минимума.

Возвратимся теперь к оптической интерпретации. Угол α между приходящим лучом и нормалью к поверхности называется углом падения, а угол β между уходящим лучом и нормалью — углом преломления. Отношение u/v скоростей зависит от двух сред, воды и воздуха, но не от геометрических обстоятельств, как например расположения точек A и B. Следовательно, условие минимума требует, чтобы синусы углов падения и преломления имели постоянное отношение, зависящее только от двух сред (называемое в настоящее время коэффициентом преломления). «Принцип наименьшего времени» Ферма приводит к закону преломления Снеллиуса, подтвержденному бесчисленными наблюдениями.

Мы восстановили, насколько сумели, рождение важного открытия. Метод решения. (которым мы воспользовались вместо решения Ферма) также достоин быть отмеченным. Наша задача имела сначала

171

физическую (оптическую) интерпретацию. Однако чтобы ее решить, мы придумали другую физическую (механическую) интерпретацию. Наше решение было решением с помощью новой интерпретации. Такие решения могут выявлять новые аналогии между различными физическими явлениями и имеют своеобразное художественное достоинство[57].

4. Открытие брахистохроны Иоганном Бернулли. Тяжелая материальная точка начинает двигаться из положения покоя в точке A и скользит без трения по наклонной плоскости до более низкой точки B. Эта материальная точка, начинающая двигаться из положения покоя, может также спускаться от A к B по дуге окружности, как груз маятника. Какое движение занимает меньше времени: движение по прямой или по дуге окружности? Галилей думал, что более быстрым является спуск по дуге окружности. Иоганн Бернулли вообразил в вертикальной плоскости, проходящей через A и B, произвольную кривую, соединяющую эти две точки. Существует бесконечно много таких кривых, и он стал разыскивать кривую, которая делает время спуска минимальным; эта кривая называется «кривой наиболее быстрого спуска», или «брахистохроной». Мы хотим понять замечательное по богатству фантазии решение этой задачи, принадлежащее Иоганну Бернулли.

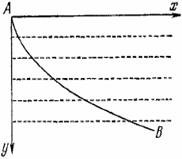
Рис. 9.11. Путь материальной точки.

Поместим произвольную кривую, спускающуюся от A к B, в систему координат см. рис. 9.11. Выберем точку A в качестве начала координат; ось x направим горизонтально[58], а ось y — вертикально вниз. Рассмотрим момент, когда материальная точка, скользящая по кривой, проходит некоторую точку (x, y) с некоторой скоростью v. Имеем соотношение

которое было хорошо знакомо Бернулли; мы выводим его сегодня из закона сохранения энергии. Иными словами, каким бы ни был путь спуска, достигнутая скорость v зависит только от y, глубины спуска:

v = (2gy)^1/2. (1)

Что это означает? Попытаемся интуитивно понять значение этого основного факта.

Проведем горизонтальные прямые (см. рис 9.11), делящие плоскость, в которой спускается материальная точка, на узкие горизон-

172

тальные слои. Спускающаяся материальная точка пересекает эти слои один за другим. Скорость не зависит от пути, который она проходит, но зависит только от слоя, который она в данный момент пересекает; ее скорость меняется от слоя к слою. Где мы встречали такую ситуацию? Когда к нам падает свет солнца, он пересекает несколько слоев воздуха, каждый из которых имеет различную плотность; поэтому скорость света меняется от слоя к слою. Предложенная механическая задача допускает новую, оптическую интерпретацию.

Мы видим теперь рис. 9.11 в новом контексте. Мы рассматриваем эту фигуру как изображающую оптически неоднородную среду. Эта среда расслоена, состоит из слоев различной плотности; скорость света в горизонтальном слое на глубине y равна (2gy)^1/2. Свет, пересекающий эту среду от A до B (от одной из данных точек до другой), мог бы распространяться по различным кривым. Однако свет выбирает наиболее быстрый путь; в действительности он распространяется по кривой, делающей время распространения минимальным, Поэтому действительный путь света, пересекающего описанную неоднородную, расслоенную среду от A до B, есть брахистохрона! Однако действительный путь света подчиняется закону преломления Снеллиуса: решение внезапно оказывается в пределах досягаемости. Новая интерпретация Иоганна Бернулли, возникшая при большом участии фантазии, делает доступной задачу, которая представлялась совершенно новой и недоступной.

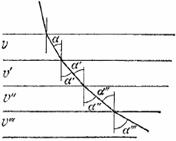
Рис. 9.12. Путь света.

Остается еще кое-какая работа, но она требует несравненно меньше оригинальности. Чтобы сделать закон Снеллиуса применимым в его знакомой форме (рассмотренной нами в предыдущем § 3), снова слегка изменим нашу интерпретацию рис. 9.11: скорость v должна меняться вместе с y не непрерывно, бесконечно малыми шагами, но разрывно, малыми шагами. Представим себе несколько горизонтальных слоев из прозрачного материала (несколько пластинок из стекла), причем каждый слой немного оптически отличается от соседних с ним слоев. Пусть v, v′, v″, v‴, … — скорости света в последовательных слоях, и пусть свет, пересекающий их один за другим, составляет, соответственно, α, α′, α″, α‴, … с вертикалью; см. рис. 9.12. По закону Снеллиуса (см. § 3)

Теперь мы можем от среды, состоящей из узких пластинок, возвратиться к нашей расслоенной среде, в которой v непрерывно меняется с глубиной. (Пусть пластинки становятся бесконечно узкими.)

173

Мы видим, что вдоль пути света

(2)

Пусть β — угол, образованный касательной к кривой с горизонталью. Тогда

и значит

sin α = cos β = (1 + y′)^{— 1/2}. (3)

Сопоставим равенства (1), (2) и (3) (выведенные соответственно из механики, оптики и дифференциального исчисления), введем подходящее обозначение для постоянной, входящей в (2), и в результате получим

y(1 + y′²) = c,

где с — положительная постоянная. Мы получили для брахистохроны дифференциальное уравнение первого порядка. Отыскание кривых, удовлетворяющих такому уравнению, было задачей, известной Бернулли. Нам неn необходимости входить здесь в детали (см., тем не менее, пример 31): брахистохрона, определенная этим дифференциальным уравнением, оказалась циклоидой. (Циклоида описывается точкой окружности, катящейся по прямой линии[59]; в нашем случае эта прямая — ось x, и окружность катится по оси x снизу.)

Отметим, однако, что интуитивно, не прибегая к формулам, мы можем видеть, что закон Снеллиуса приводит к дифференциальному уравнению. Действительно, этот закон определяет направление последовательных элементов пути, изображенных на рис. 9.12, и в точности то же самое делает дифференциальное уравнение.

Решение Иоганна Бернулли задачи о брахистохроне, которое мы здесь разобрали, имеет своеобразную художественную прелесть. Рассматривая рис. 9.11 или рис. 9.12, мы можем наглядно видеть ключевую идею решении. Если мы можем видеть эту идею ясно, без усилий, сознавая, что́ она за собой влечет, то мы можем заметить, что перед нами настоящее произведение искусства.

Ключевой идеей решении Иоганна Бернулли является, конечно, новая интерпретация. Геометрический чертеж (рис. 9.11 или 9.12) последовательно понимается в двух различных интерпретациях, он рассматривается в двух различных «контекстах»: сначала в механическом контексте, затем в оптическом контексте. Не всякое ли открытие состоит в неожиданном соприкосновении и последующей интерпретации двух различных контекстов?[60]

5. Открытие Архимедом интегрального исчисления[61]. Так уж случилось, что одно из величайших математических открытий всех времен

174

имело своим источником физическую интуицию. Я имею в виду открытие Архимедом той ветви науки, которую сегодня мы называем интегральным исчислением. Архимед нашел площадь параболического сегмента, объем шара и еще около дюжины подобных результатов с помощью единообразного метода, в котором важную роль играет идея равновесия. Как он сам сказал, он «исследовал несколько математических задач средствами механики»[50].

Если мы хотим понять работу Архимеда, то нам нужно кое-что внять о состоянии знаний, от которых он отправлялся. Во времена Архимеда геометрия греков достигла вершины своего развития; Эвдокс и Эвклид были его предшественниками, Аполлоний — его современником. Мы должны упомянуть несколько характерных обстоятельств, которые, возможно, оказали влияние на открытие Архимеда.

Как сообщает сам Архимед, Демокрит нашел объем конуса; он установил, что этот объем равен одной трети объема цилиндра с тем же основанием и с той же высотой. Мы ничего не внаем о методе Демокрита, но, по-видимому, имеются некоторые основания подозревать, что он рассматривал то, что мы сегодня назвали бы переменным поперечным сечением конуса, параллельным его основанию[51].

Эвдокс был первым, кто доказал утверждение Демокрита. Доказывая этот и подобные результаты, он изобрел свой «метод исчерпывания» и установил стандарт строгости для греческой математики.

Мы должны ясно осознать, что греки в определенном смысле знали «координатную геометрию». Для изучения геометрических мест точек на плоскости они обычно рассматривали расстояние движущейся точки от двух фиксированных осей отсчета. Если сумма квадратов этих расстояний постоянна и оси отсчета взаимно перпендикулярны, то геометрическое место точек есть окружность — это предложение принадлежит к координатной геометрии, но еще не к аналитической геометрии. Аналитическая геометрия начинается в тот момент, когда мы выражаем упомянутое соотношение в алгебраических символах в виде

x² + y² + a².

Механика греков никогда не достигала такого высокого уровня, как их геометрия, и начала развиваться значительно позднее. Если мы правильно оценим неясные рассмотрения Аристотеля и других, то сможем сказать, что механика как наука началась с Архимеда. Он, как знает каждый, открыл закон плавающих тел. Он открыл

175

также принцип рычага и главные свойства центра тяжести, которые нам вскоре понадобятся.

Теперь мы подготовлены к обсуждению наиболее эффектного примера из работы Архимеда; мы хотим его методом найти объем шара[62]. Архимед рассматривает шар как тело, образованное вращающейся окружностью, а окружность он рассматривает как геометрическое место точек, характеризуемое соотношением между расстояниями переменной точки от двух фиксированных взаимно перпендикулярных осей отсчета. Записанное в современных обозначениях, это соотношение имеет вид

x² + y² = 2ax

— уравнение окружности радиуса a, касающейся оси y в начале координат. См. рис. 9.13, который лишь слегка отличается от оригинального чертежа Архимеда; эта окружность, вращаясь вокруг оси x, образует шар. Я думаю, что применение современных обозначений не нарушает идеи Архимеда Наоборот, мне кажется, что эти обозначения заставляют думать. Они подсказывают мотивы, которые могут привести нас сегодня к идее Архимеда и которые, быть может, не слишком отличаются от мотивов, которые привели самого Архимеда к его открытию.

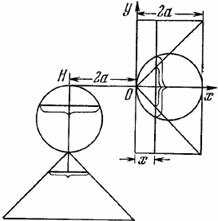
Рис. 9.13. Рождение интегрального исчисления.

В уравнении окружности имеется член y². Заметим, что πy² есть площадь переменного поперечного сечения шара. Однако[63] Демокрит нашел объем конуса, исследуя изменение его поперечного сечения. Это приводит нас к мысли переписать уравнение окружности в виде

πx² + πy² = π2ax

Теперь мы можем πx² интерпретировать как переменное поперечное сечение конуса, образованного вращением прямой y = x[64] вокруг оси x; см. рис. 9.13. Это наталкивает на мысль отыскать аналогичную интерпретацию для остающегося члена π2ax. Если мы не видим такой интерпретации, то можем попытаться переписать уравнение еще и в других формах, и, таким образом, может случиться, что нам придет в голову записать его в виде

2a(πy² + πx²) = xπ(2a)². (A)

Многое сосредоточено в этом уравнении (A). Рззглядывзя уравнение (A), отмечая различные входящие в него длины и площади

176

и подходящим образом располагая их на чертеже, мы можем оказаться свидетелями рождения великой идеи; она родится из тесного соединения формулы (A) с рис. 9.13.

Мы замечаем площади трех круглых дисков[65], πy², πx² и π(2a)². Эти три круга являются пересечениями одной и той же плоскости с тремя телами вращения. Плоскость перпендикулярна к оси x и находится на расстоянии x от начала O. Эти три тела вращения — шар, конус и цилиндр. Они описываются тремя линиями, имеющими, соответственно, уравнения (A), y = x и y = 2a, когда правая часть рис. 9.13 вращается вокруг оси x. Конус и цилиндр имеют одно и то же основание и одну и ту же высоту. Радиус их общего основания и их общая высота имеют одинаковую длину 2a. Вершина конуса находится в начале O.

Архимед различным образом подходит к дискам, площади которых находятся в равных частях уравнения (A). Он оставляет диск радиуса 2a, поперечное сечение цилиндра, в его первоначальном положении, на расстоянии x от начала. Однако он перемешает диски радиусов y и x, соответственно, поперечные сечения шара и конуса, из их первоначального положения и переносит их в точку H оси x с абсциссой — 2a. Подвесим эти диски радиусов y и x так, чтобы их центр находился вертикально под точкой H, с помощью нити нулевого веса, см. рис. 9.13. (Эта нить — добавление нулевого веса к оригинальному чертежу Архимеда.)

Рассмотрим ось x как рычаг, жесткий брус нулевого веса, а начало O — как его точку опоры, или точку подвеса. В уравнение (A) входят моменты. (Момент есть произведение силы на плечо рычага.) Уравнение (A) выражает тот факт, что момент двух дисков в левой части равен моменту одного диска в правой части, и, значит, в силу механического закона, открытого Архимедом, рычаг находится в равновесии.

Когда x меняется от O до 2a, мы получаем все поперечные сечения цилиндра; эти поперечные сечения заполняют цилиндр. Каждому поперечному сечению цилиндра соответствуют два поперечных сечения тел, подвешенных в точке H, и эти поперечные сечения заполняют, соответственно, шар и конус. Как и их соответствующие поперечные сеченая, шар и конус, подвешенные в H, находятся в равновесии с цилиндром. Следовательно, по механическому закону Архимеда, их моменты должны быть равны. Обозначим буквой V объем шара, вспомним выражение для объема конуса (принадлежащее Демокриту), а также для объема цилиндра и очевидное положение его центра тяжести. Переходя от моментов поперечных сечений к моментам соответствующих тел, приходим от уравнения (A) к уравнению

(B)

177

которое легко дает[52]

Вновь просматривая предыдущее, мы видим, что решающим шагом является переход от (А) к (B), от заполняющих поперечных сечений к полным телам. Однако этот шаг только эвристически допущен, а не логически оправдан. Он правдоподобен, даже очень правдоподобен, но не доказателен. Это догадка, а не доказательство. И Архимед, представляющий великие традиции греческой математической строгости, очень хорошо знает это: «Хотя это всем вышеприведенным рассуждением и не доказано, но все же оно производит впечатление, что окончательный вывод верен»[53]. Эта догадка является, однако, догадкой с будущим. Идея выходит далеко за пределы требований рассматриваемой задачи и имеет неизмеримо больший размах. Переход от (А) к (B), от поперечного сечения ко всему телу есть, на более современном языке, переход от бесконечно малой части к целой величине, от дифференциала к интегралу. Этот переход — великое начало, и Архимед, который был достаточно великим человеком, чтобы видеть себя в исторической перспективе, очень хорошо знал это: «Он [этот метод] может принести математике немалую пользу; я предполагаю, что некоторые современные нам или будущие математики смогут при помощи указанного метода найти и другие теоремы, которые нам еще не приходили в голову»[54].

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ IX

1. На плоскости даны точка P и две пересекающиеся прямые l и m, причем ни одна из этих прямых не проходит через P. Пусть Y — переменная точка прямой l, а Z — переменная точка прямой m. Определите Y и Z так, чтобы периметр ∆PYZ был наименьшим.

Дайте два решения: одно с помощью физических рассмотрений, а другое — с помощью геометрии.

2. На плоскости даны три окружности, каждая из которых является внешней по отношению к любой другой. Найдите треугольник с минимальным периметрам, имеющий по одной вершине на каждая окружности.

Дайте две различные физические интерпретации.

3. _Треугольник с минимальным периметром, вписанный в данный треугольник. Дан ∆ABC. Найдите три точки X, Y и Z, соответственно, на сторонах BC, CA, AB треугольника так, чтобы периметр ∆XYZ был минимальным.

Дайте две различные физические интерпретации.

178

4. Обобщите пример 3.

5. Критически пересмотрите решение примера 1. Ко всем ли случаям оно применимо?

6. Критически пересмотрите решение примера 3. Ко всем ли случаям оно применимо?

7. Дайте строгое решение примера 3 для остроугольного треугольника. [Частное изменение, пример 1, пример 5.]

8. Критически пересмотрите решения § 1 (4) и § 2 (2) задачи о транспортном центре. Ко всем ли случаям они применимы?

9. Транспортный центр четырех точек в пространстве. Дан тетраэдр с вершинами в точках A, B, C и D. Предположим, что существует такая точка X внутри тетраэдра, для которой сумма ее расстояний от четырех вершин

AX + BX + CX + DX

является минимальной. Покажите, что углы ∠AXB и ∠ CXD равны и делятся пополам одной и той же прямой; укажите другие пары подобным же образом связанных углов. [Знаете ли вы задачу, родственную этой? Аналогичную задачу? Могли ли бы вы воспользоваться ее результатом или методом ее решения?]

10. Транспортный центр четырех точек на плоскости. Рассмотрите крайний случай примера 9, когда точки A, B, C и D лежат в одной плоскости, являются вершинами выпуклого четырехугольника ABCD. Остается ли утверждение примера 9 справедливым в этом крайнем случае?

11. Транспортная сеть для четырех тачек. Пусть A, B, C и D — четыре фиксированных точки, а X и Y — переменные точки на плоскости. Если минимум суммы пяти расстояний AX + BX+ XY + YC + YD достигается так, что все шесть точек A, B, C, D, X и Y различны, то три прямые XA, XB и XY одинаково наклонены одна к другой, и это же верно для трех прямых YC, YD и YX.

12. Разверните и выпрямите. Существует еще другая полезная интерпретация рис. 9.3. Начертите l, A*X и XB на листе прозрачной бумаги, затем согните лист по прямой l: вы получите рис. 9.1 [с A* вместо A). Представьте себе, что рис. 9.1 первоначально начерчен этим искусственным способом на согнутом прозрачном листе. Чтобы найти положение точки X, обращающее AX + XB в минимум, разверните лист, начертите прямую от A [илиР вернее, A* на рис. 9.3) к B, и затем снова согните лист.

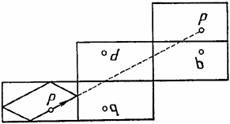
Рис. 9.14. Отраженный бильярдный стол.

13. Бильярд. На прямоугольном бильярдном столе в точке P находится шар. Требуется ударить шар в таком направлении, чтобы после четырех последовательных отражений от четырех сторон прямоугольника шар возвратился в свае первоначальное положение P. [Рис. 9.14.]

14. Геофизическое исследование. В точке E горизонтальной поверхности земли происходит взрыв. Звук этого взрыва распространяется внутрь земли и отражается наклонной плоскостью пласта OR, составляющею угол α с поверхностью земли. Звук, приходящий из E, может достичь контрольного поста L в другой точке земной поверхности n различными путями. [Один из этих n путей построен на рис. 9.15 методом примера 12.) Предполагая, что n (отмеченное соответствующим прибором) дано, укажите пределы, между которыми заключен угол α.

179

15. В пространстве даны прямая l и две точки A и B, не лежащие на l. На прямой l найдите точку X, для которой сумма ее расстояний от двух данных точек AX + XB является наименьшей.

[Знаете ли вы какую-нибудь задачу, родственную этой? Более частную задачу? Могли ли бы вы воспользоваться ее результатом или методом ее решения?]

Рис. 9.15. Подземные отражения.

16. Решите пример 15, пользуясь касательной поверхностью уровня.

17. Решите пример 15 сгибанием бумаги.

18. Решите пример 15 с помощью механической интерпретации. Находится ли решение в согласии с примерами 16 и 17?

19. В пространстве даны три скрещивающиеся прямые a, b и c. Покажите, что треугольник наименьшего периметра, имеющий по одной вершине на каждой из данных прямых, обладает следующим свойством: прямая, соединяющая его вершину на прямой a с центром вписанного в него круга, перпендикулярна к a.

20. Рассмотрите частный случай примера 19, когда три скрещивающиеся прямые являются тремя ребрами куба. Где находятся вершины искомого треугольника? Где находится центр вписанного в него крута? Чему равен его периметр, если объем куба равен 8a³?

21. В пространстве даны три скрещивающиеся прямые a, b и c. Пусть X перемещается по a, Y по b, Z по c и T свободно перемещается в пространстве. Найдите минимум суммы XT + YT + ZT.

22. Рассмотрите частный случай примера 21, подобно тому как в примере 31 рассмотрен частный случай примера 19.

23. Кратчайшие линии на многогранной поверхности. Передняя и задняя стены прямоугольной комнаты являются квадратами; комната имеет 10 м в длину, 4 м в ширину и 4 м в высоту. На передней стене, на высоте 3,5 м от пола и на одинаковом расстоянии от боковых стен находится паук. На противоположной стене на высоте 0,5 м от пола и также на одинаковом расстоянии от боковых стен паук замечает муху. Покажите, что паук, чтобы постичь муху, должен проползти по стенам, или потолку, или полу, меньше чем 14 м. [Пример 17.]

24. Кратчайшие (геодезические) линии на кривой поверхности. Кривую поверхность мы рассматриваем как предел многогранника. Когда многогранник приближается к кривой поверхности, число его граней стремится к ∞, наибольшая диагональ любой грани стремится к 0 и грани стремятся стать касательными к поверхности.

На многогранной поверхности кратчайшей линией между двумя точками является ломаная. Она может быть плоской ломаной, все точки которой лежат в одной плоскости, или она может быть пространственной ломаной, точки которой не содержатся в одной плоскости. [Оба случая можно проиллюстрировать решением примера 23, первый случай — (1), второй случай — (2) и (3).]

Кратчайшая линия на кривой поверхности называется «геодезической» потому, что кратчайшие линии играют важную роль в геодезии, учении о земной поверхности. Геодезическая линия может быть плоской кривой, целиком содержащейся

180

в одной плоскости, или она макет быть «пространственной кривой» («скрученной» кривой), точки которой не содержатся в одной плоскости. Как бы то ни было, геодезическая линия должна иметь какую-то внутреннюю геометрическую связь с поверхностью, на которой она является кратчайшей линией. Какова эта связь?

(1) Рассмотрим ломаную ABC...L. Даже если ABC...L — пространственная ломаная, два соседних ее отрезка, например HI и IJ, лежат в одной плоскости. Если ABC...L — кратчайшая линия на многогранной поверхности между своими концами A и L, то каждая из промежуточных вершин B, C, D, …, H, I, J, …, K лежит на ребре многогранника. Плоскость, содержащая отрезки HI и IJ, содержит и биссектрису ∠HIJ, и эта биссектриса перпендикулярна ребру многогранника, проходящему через I; см. пример 16 или пример 18.

Рассмотрим кривую. Даже если эта кривая скрученная, ее бесконечно малая (очень короткая) дуга может рассматриваться как плоская (почти плоская) дуга. Плоскость бесконечно малой дуги есть соприкасающаяся плоскость в ее середине. Эта соприкасающаяся плоскость аналогична плоскости, в которой лежат два соседних отрезка пространственной ломаной. Если кривая является геодезической линией, т. е. кратчайшей линией на поверхности, то аналогия подсказывает, что соприкасающаяся плоскость геодезической линии в произвольной точке проходит через нормаль к поверхности в этой тачке.

(2) Геодезическая линия физически может быть интерпретирована как резиновая лента, натянутая на гладкую поверхность (т. е. поверхность, по которой всякое тело скользит без трения). Исследуем равновесие маленького участка этой резиновой ленты. Силы, действующие на этот участок — два натяжения равной величины, действующие по касательным в двух концах нашей маленькой дуги, и реакция поверхности, которая, ввиду отсутствия трения в каждой точке, направлена по нормали к поверхности. Равнодействующая сил реакции поверхности и два натяжения в концах дуги находятся в равновесии. Следовательно, эти три силы параллельны одной и той же плоскости. Однако две «близкие касательные» определяют соприкасающуюся плоскость, которая, таким образом, содержит нормаль к поверхности.

(3) Каждая дуга геодезической линии является геодезической линией. Действительно, если кривая имеет участок, который не является кратчайшим между своими концами и, следовательно, макет быть заменен более короткой дугой между этими концами, то вся кривая не может быть кратчайшей линией. Поэтому естественно ожидать, что геодезическая линия обладает каким-либо отличительным свойством в каждой своей точке. Свойство, которое показывают два очень различных эвристических рассмотрения (1) и (2), является свойством этого рода.

(4) Подыщите примеры, чтобы проверить эвристически полученный результат. Каковы кратчайшие линии на сфере? Обладают ли они указанным свойством? Обладают ли этим свойством другие линии на сферической поверхности?

25. Материальная точка движется без трения по гладкой жесткой поверхности. Никакие внешние силы (такие, как сила тяжести) на эту точку не действуют (исключая, конечно, реакцию поверхности). Приведите причины, по которым следует ожидать, что точка описывает геодезическую линию.

26. Построение посредством сгибания бумаги. Найдите многоугольник, вписанный в круг, если задан порядок и величина его сторон.

Пусть a₁, a₂, a₃, …, a_n обозначают заданные длины. За стороной длины a₁ следует сторона длины a₂, за ней — сторона длины a₃ и т. д.; за стороной длины a_n следует сторона длины a₁. Подразумевается, что любая из длин a₁, a₂, …, a_n меньше, чем сумма остальных n—1 длин.

Существует прекрасное решение посредствам сгибания бумаги. Проведите a₁, a₂, …, a_n на картоне как последовательные хорды достаточно большого круга так, чтобы две соседние хорды имели общий конец. Проведите радиусы из этих концов в центр круга. Вырежьте многоугольник, ограниченный n хордами и двумя крайними радиусами. Согните картон вдоль n—1 других радиусов и склейте два радиуса, вдоль которых картон был разрезан. Вы получили таким образом открытую многогранную поверхность; она состоит из n жестких равнобедренных

181

`треугольников, ограничена n свободными ребрами длин, соответственно, a₁, a₂, …, a_n и имеет n двугранных углов, которые еще могут изменяться. (Мы предполагаем, что n > 3.)

Что вы можете делать с этой многогранной поверхностью, чтобы решить предложенную задачу?[66]

27. Бросается кость. Масса внутри тяжелого жесткого выпуклого многогранника может быть распределена неравномерно. Фактически мы можем представить себе подходящее неоднородное распределение массы, центр тяжести которой совпадает с произвольно указанной внутренней точкой многогранника. Если бросить многогранник на горизонтальный пол, то он остановится на одной из своих граней. Это дает механический довод для следующего геометрического предложения.

Если дан выпуклый многогранник P и некоторая точка C внутри P, то мы можем найти грань F многогранника P, обладающую следующим свойством: основание перпендикуляра, опущенного из С на плоскость грани F, есть внутренняя точка P.

Найдите геометрическое доказательство этого предложения. (Заметьте, что грань F может, но не обязана однозначно определяться сформулированным свойством.)

28. Всемирный потоп. На контурной карте существует три типа замечательных точек: вершины, перевалы (или седловые точки с горизонтальной касательной плоскостью) и «котловины» (на рис. 8.7 В — вершина, П — перевал). «Котловина» — наиболее глубокая точка в дне долины, из которой вода не находит никакого стока. Котловина есть «перевернутая» вершина: рассмотрите на контурной карте любую линию уровня высоты h над уровнем моря как если бы она имела над уровнем моря высоту — h. Тогда карта «перевернута»; она становится картой ландшафта под морем, вершины становятся котловинами, котловины становятся вершинами, но перевалы остаются перевалами. Существует замечательная связь между этими тремя типами точек.

Допустим, что на острове имеется В вершин, К котловин и П перевалов. Тогда

В + К = П + 1.

Чтобы интуитивно вывести эту теорему, вообразим, что неперестающий дождь заставил озеро, окружающее остров, подниматься до тех пор, пока, наконец, весь остров не был затоплен. Мы можем считать, что все В вершин имеют одинаковую высоту и что все К котловин находятся на уровне озера или ниже его. В самом деле, мы можем вообразить, что вершины поднялись, а котловины понизились, но их число не изменилось. Когда дождь начинает идти, в котловинах собирается вода; вначале мы имеем, считая окружающее остров озеро,

К + 1 озер и 1 остров.

Непосредственно перед тем как остров скроется под водой, из-под воды выступают только вершины, и, таким образом, в конце мы имеем

1 озеро и В островов[67].

Как происходил переход?[68]

Вообразим, что в какой-то момент на одной и той же высоте находится несколько озер. Если нет никаких находящихся на этой высоте перевалов, то вода может еще немного подняться, не меняя числа озер или числа островов. Когда, однако, поднимающаяся вода как раз достигнет перевала, малейший последующий подъем ее уровня или объединит два прежде отделенных озера, или изолирует участок земли. Поэтому каждый перевал или на одну единицу уменьшает число озер, или на одну единицу увеличивает число островов. Рассматривая полное изменение, получаем

(К + 1 — 1) + (В — 1) = П;

в этом и состоит наша теорема.

182

(а) Допустите теперь, что на всем земном шаре имеется В вершин, К котловин и П перевалов (некоторые из них под водой), и покажите, что

В + К = П + 2.

(b) Последнее соотношение напоминает нам теорему Эйлера [см. §§ 3.1—3.7 и примеры 3.1—3.9). Могли бы вы воспользоваться теоремой Эйлера для построения геометрического доказательства результата, только что полученного с помощью интуитивных соображений? [Рис. 9.16 и 9.17 показывают важные куски более полной карты, на которой указано не только несколько линий уровня, но и несколько «линий наиболее крутого спуска», перпендикулярных к линиям уровня. Эти два типа линий разбивают поверхность земли на треугольники и четырехугольники. Ср. пример 3.2.]

Рис. 9.16. Окрестность вершины.	Рис. 9.17. Окрестность перевала.

(c) Имеются ли какие-нибудь замечания по поводу метода?

29. Не слишком глубоко[55][69]. Чтобы найти глубину колодца D, вы бросаете в колодец камень и измеряете время t от момента бросания камня до момента, когда вы услышите, что камень ударился о воду.

(а) Даны ускорение силы тяжести g и скорость звука C. Выразите d через g, c и t (пренебрегая сопротивлением воздуха).

(b) Если колодец не слишком глубок, то скорость камня даже в момент падения будет составлять малую долю скорости звука, и, таким образом, мы можем ожидать, что значительно бо́льшая часть измеренного времени t уйдет на падение камня. Поэтому следует ожидать, что

d = gt²/2 — поправка,

где поправка относительно мала, когда t мало.

Чтобы проверить эту догадку, разложите выражение, полученное в качестве ответа в (а), по степеням t и сохраните первые два не равных нулю члена.

(c) Что в этом примере вы рассматривали бы как типичное?

30. Полезный крайний случай. Эллипс, вращающийся вокруг своей большой оси, описывает так называемый вытянутый сфероид, или яйцевидный эллипсоид вращения. Фокусы вращающегося эллипса не вращаются: они находятся на оси вращения и также называются фокусами вытянутого сфероида. Мы могли бы изготовить эллиптическое зеркало, покрыв внутреннюю, вогнутую сторону этой поверхности полированным металлом; все лучи, приходящие из одного фокуса, отражаются таким эллиптическим зеркалом в другой фокус; ср. § 1 (3). Эллип-

183

тические зеркала на практике применяются очень редко, но существует предельный случай, очень важный в астрономии. Что происходит, если один из фокусов эллипсоида фиксирован, а другой стремится к бесконечности?

31. Решите дифференциальное уравнение брахистохроны, найденное в § 4.

32. Вариационное исчисление занимается задачами на максимум и минимум величин, зависящих от формы и размера переменной кривой. Такова задача о брахистохроне, решенная в § 4 с помощью оптической интерпретации. Задача о геодезических, или кратчайших линиях на кривой поверхности, рассмотренная в примере 24, также принадлежит к вариационному исчислению; к нему же принадлежит и «изопериметрическая задача», о которой будет идти речь в следующей главе. Физические рассмотрения, которые, как мы видели, могут решать различные задачи на максимум и минимум, могут решать и некоторые задачи вариационного исчисления. Наметим пример.

Найти кривую данной длины и с данными концами, имеющую центр тяжести наименьшей высоты. Предполагается, что плотность постоянна вдоль кривой, которую мы рассматриваем как однородную веревку, или цепь. Когда центр тяжести цепи достигает своего наиболее низкого положения, цепь находится в равновесии. Теперь мы можем исследовать равновесие цепи, рассматривая действующие на нее силы, ее вес и ее натяжение. Это исследование приводит к дифференциальному уравнению, которое определяет искомую кривую, цепную линию. Мы не входим в детали. Мы хотим только отметить, что намеченное решение имеет ту же основную идею, что и механические решения, рассмотренные в 3 2.

33. От равновесия поперечных сечений к равновесию тел. Архимед не сформулировал в явной форме общий принцип своего метода, но он применил его к нескольким примерам, вычисляя объемы, площади и центры тяжести, и разнообразив этих примеров делает этот принцип совершенно ясным. Применим вариант метода Архимеда, изложенный в § 5, к некоторым из его примеров.

Докажите Предложение 7 «Метода»:

Объем шарового сегмента относится к объему конуса с тем же основанием и высотой как сумма радиуса шара и высоты дополнительного сегмента к высоте дополнительного сегмента.

34. Докажите Предложение 6 «Метода»:

Центр тяжести полушария лежит на его оси и делит эту ась так, что часть, примыкающая к вершине полушария, относится к остальной части как 5 : 3.

35. Докажите Предложение 9 «Метода»:

Центр тяжести шарового сегмента лежит на его оси и делит эту ось так, что часть, примыкающая к вершине, относится к остальной части как сумма оси сегмента и четырехкратной оси дополнительного сегмента к сумме оси сегмента и удвоенной оси дополнительного сегмента.

36. Докажите Предложение 4 «Метода»:

Объем сегмента параболоида вращения, отсеченного плоскостью, перпендикулярной оси, относится к объему конуса, имеющего то же основание и ту же высоту, что и сегмент, как 3 : 2.

37. Докажите Предложение 5 «Метода»:

Центр тяжести сегмента параболоида вращения, отсеченного плоскостью, перпендикулярной оси, лежит на оси и делит ее так, что часть, примыкающая к вершине, вдвое больше остальной части.

38. Ретроспективный взгляд на Метод Архимеда. Что было в уме Архимеда, когда он открыл свой метод, мы никогда не узнаем и можем только смутно об этом догадываться. Однако мы можем составить ясный и довольно короткий перечень таких математических правил [хорошо известных сегодня, но не сформулированных во времена Архимеда), которые нужны нам для решения современными методами задач, решенных Архимедам его методом. Нам нужны:

(1) Два общих правила интегрального исчисления.

∫cf(x)dx =∫cf(x)dx, ∫[f(x) + g(x)]dx = ∫f(x)dx + ∫g (x)dx;

с — постоянная, f(x) и g(x) — функции.

184

(2) Значения четырех интегралов:

∫ xⁿ dx = x^n—1/(n—1) для n = 0, 1, 2, 3.

(3) Геометрическая интерпретация двух интегралов:

∫ Q (x) dx, ∫ x Q (x) dx.

Здесь Q (x) означает длину в плоской геометрии и площадь в пространственной геометрии; оно обозначает в обоих случаях переменное поперечное сечение фигуры или тела, определяемое плоскостью, перпендикулярной к оси x. Первый интеграл выражает площадь или объем, второй интеграл — момент однородной площади или объема в соответствии с тем, рассматриваем ли мы задачу плоской или пространственной геометрии.

Архимед не формулировал эти правила, хотя мы не можем не думать, что он в той или иной форме ими владел. Он воздержался даже от того, чтобы сформулировать в общих выражениях процесс, лежащий в основании перехода от переменного поперечного сечения к площади или объему, от подынтегральной функции к интегралу, как мы сказали бы сегодня. Он описывал этот процесс в частных случаях, он применял его к замечательному разнообразию случаев, он, несомненно, глубоко его знал, но он рассматривал его только как эвристический метод и считал это вполне достаточной причиной для того, чтобы воздержаться от формулирования его в общем виде.

Приведите простые геометрические факты, которые могут интуитивно дать значения четырех интегралов, указанных в (2)[56].

Х. ИЗОПЕРИМЕТРИЧЕСКАЯ ЗАДАЧА

Круг — первая, наиболее простая и наиболее совершенная фигура — Прокл[57]

Lo cerchio è perfetissima[70] figura. — Данте[58]

1. Индуктивные доводы Декарта. В неоконченной работе Декарта Regulae ad Directionem Ingenii (или Правила для руководства ума, которая, кстати сказать, должна рассматриваться как одна из классических работ по логике открытия) мы находим следующее любопытное место[59]: «Чтобы показать посредством энумерации, что периметр круга меньше, чем периметр любой другой фигуры той же площади, нет необходимости исследовать все возможные фигуры, но достаточно доказать это на нескольких из них, чтобы путем индукции вывести то же самое для всех других фигур».

Чтобы понять смысл этой выдержки, выполним действительно то, что предлагает Декарт. Сравним круг с несколькими другими фигурами: треугольниками, прямоугольниками и круговыми секторами. Возьмем два треугольника: равносторонний и равнобедренный прямоугольный (с углами, соответственно, 60°; 60°; 60° и 90°, 45°, 45°). Форма прямоугольника характеризуется отношением его ширины к его высоте; мы выберем отношения 1 : 1 (квадрат), 2 : 1, 3 : 1 и 3 : 2. Форма сектора круга определяется углом в пентр~ мы выберем углы 180°, 90° и 60° (полукруг, квадрант и секстант). Допустим, что все эти фигуры имеют одинаковую площадь, скажем 1 см². Затем вычислим длину периметра каждой фигуры в сантиметрах. Полученные числа собраны в следующую таблицу (см. стр. 186); порядок фигур выбран так, чтобы периметры возрастали, когда мы читаем их сверху вниз.

Из десяти перечисленных фигур, имеющих одинаковую площадь, круг, указанный первым, имеет наименьший периметр. Можем ли мы отсюда посредством индукции вывести, как, по-видимому, предлагает Декарт, что круг имеет наименьший периметр не только среди десяти перечисленных фигур, но и среди всех возможных

186

фигур? Никоим образом. Но нельзя отрицать, что наш сравнительно короткий список очень сильно толкает к этой общей теореме. В сущности, настолько сильно, что если бы мы и добавили к нему еще одну или две фигуры, он не мог бы толкать к ней намного сильнее.

Таблица I

Периметры фигур равной площади

Круг	3,55
Квадрат	4,00
Квадрант	4,03
Прямоугольник 3 : 2	4,08
Полукруг	4,10
Секстант	4,21
Прямоугольник 2 : 1	4,24
Равносторонний треугольник	4,56
Прямоугольник 3 : 1	4,64
Равнобедренный прямоугольный треугольник	4,84

Я склонен верить, что Декарт, когда он писал приведенное место, думал об этом последнем, более тонком обстоятельстве. Он намеревался, я думаю, сказать, что удлинение этого списка не оказало бы на нашу веру большого влияния

2. Скрытые доводы. «Из всех плоских фигур равной площади наименьший периметр имеет круг». Назовем это утверждение, подкрепленное табл. I, изопериметрической теоремой[60]. Таблица I, построенная в соответствии с предложением Декарта, является довольно убедительным индуктивным доводом в пользу изопериметрической теоремы. Но почему этот довод кажется убедительным?

Представим себе до некоторой степени сходную ситуацию. Выберем десять деревьев из десяти различных знакомых видов. Измерим удельный вес древесины каждого дерева и выберем дерево, древесина которого имеет наименьший удельный вес. Разумно ли было бы только на основании этих наблюдений верить, что вид дерева, имеющий наиболее легкую древесину среди десяти исследованных видов, имеет наиболее легкую древесину и среди всех существующих видов деревьев? Верить этому было бы не только не разумно, но глупо.

В чем же отличие от случая круга? Мы расположены в пользу круга. Круг — наиболее совершенная фигура; мы охотно верим, что вместе с другими своими совершенствами круг для данной площади имеет наименьший периметр. Индуктивный довод, высказанный Декартом, кажется таким убедительным потому, что он подтверждает предположение, правдоподобное с самого начала.

187

«Круг — наиболее совершенная фигура» — это традиционная фраза. Мы находим ее в сочинениях Данте (1265—1321), Прокла (410—485) и еще более ранних авторов. Смысл сентенции неясен, но за ней может скрываться нечто большее, чем простая традиция.

3. Физические доводы. «Из всех тел равного объема наименьшую поверхность имеет шар». Назовем это утверждение «изопериметрической теоремой в пространстве».

Изопериметрической теореме в пространстве, как и на плоскости, мы склонны верить без какого-либо математического доказательства, В пользу шара мы расположены, пожалуй, даже больше, чем в пользу круга. В самом деле, кажется, что сама природа расположена в пользу шара. Дождевые капли, мыльные пузыри, Солнце, Луна, наша Земля, планеты — шарообразны или почти шарообразны. Немножко зная физику поверхностного натяжения, мы можем научиться изопериметрической теореме у мыльного пузыря.

Однако, даже если мы не знаем серьезной физики, к изопериметрической теореме нас могут привести совсем примитивные рассмотрения. Мы можем научиться ей у кота. Я думаю вы видели, что делает кот, когда в холодную ночь он приготовляется ко сну: он поджимает лапы, свертывается и таким образом делает свое тело насколько возможно шарообразным. Он делает так, очевидно, чтобы сохранить тепло, сделать минимальным выделение тепла через поверхность своего тела. Кот, не имеющий ни малейшего намерения уменьшить свой объем, пытается уменьшить свою поверхность. Он решает задачу о теле с данным объемом и наименьшей поверхностью, делая себя возможно более шарообразным. Судя по всему, он имеет некоторое знакомство с изопериметрической теоремой.

Физика, на которой основано это рассмотрение, крайне груба[61]. Однако это рассмотрение убедительно и даже ценно как своего рода предварительное подкрепление для изопериметрической теоремы. Неуловимые доводы в пользу шара или круга, на которые выше был сделан намек (§ 2), начинают сгущаться. Не являются ли они доводами физической аналогии?

4. Индуктивные доводы лорда Рэлея[71]. Немногим более чем через двести лет после смерти Декарта физик лорд Рэлей исследовал тоны мембран. Пергамент, натянутый на барабан, есть «мембрана» (или, вернее, разумное приближение к математической идее мембраны), если только он сделан очень тщательно и так натянут, что является повсюду однородным. Барабаны обычно имеют круглую форму, но

188

в конце концов мы могли бы делать барабаны эллиптической или многоугольной, или любой другой формы. Барабан любой формы может издавать различные тоны, из которых наиболее низкий тон, называемый основным тоном, обычно является наиболее сильным. Лорд Рэлей сравнивал основные тоны мембран различной формы, но равной площади и подчиненных одним и тем же физическим условиям. Он составил табл. II, очень похожую на нашу табл. I в § 1. В этой табл. II перечисляются те же формы, что и в табл. I, но в несколько ином порядке, и для каждой формы приводится высота (частота) основного тона[62].

Таблица II

Основные частоты мембран равной площади

Круг................................	4,261
Квадрат.............................	4,443
Квадрант............................	4,551
Секстант............................	4,616
Прямоугольник 3 : 2...................	4,624
Равносторонний треугольник...........	4,774
Полукруг............................	4,803
Прямоугольник 2 : 1...................	4,967
Равнобедренный прямоугольный треугольник.............................	4,967
Прямоугольник 3 : 1...................	5,736

Из десяти перечисленных мембран, имеющих одну и ту же площадь, первая, круглая, мембрана имеет наиболее низкий основной тон. Можем ли мы отсюда по индукции заключить, что круг имеет наиболее низкий тон из всех форм?

Конечно, не можем; индукция никогда не дает возможности сделать окончательное заключение. Но она толкает к такому заключению очень сильно, даже сильнее, чем в предыдущем случае. Мы знаем (и лорд Рэлей, и его современники также знали), что из всех фигур с данной площадью круг имеет наименьший периметр и что эта теорема может быть математически доказана. Помня об этом геометрическом минимальном свойстве круга, мы склонны верить, что круг имеет и физическое минимальное свойство, к которому толкает табл. II. На наше суждение оказывает влияние аналогия, а аналогия имеет большое влияние.

Сравнение табл. I и II чрезвычайно поучительно. Оно наводит на различные другие размышления, которые мы не пытаемся теперь обсуждать[63].

5. Выведение следствий. Мы должны обозреть различные основания в пользу изопериметрической теоремы, которые конечно, недо-

189

статочны, чтобы ее доказать, но достаточны, чтобы сделать ее разумным предположением. Физик, исследующий предположение в своей науке, выводит из него следствия. Эти следствия могут находиться в согласии с фактами или же им противоречить, и физик придумывает эксперименты, чтобы выяснить, что же имеет место в действительности. Математик, исследующий предположение в своей науке, может пойти аналогичным путем. Он выводит из своего предположения следствия. Эти следствия могут быть верными или неверными, и математик пытается выяснить, что же имеет место в действительности.

Пойдем по этому пути при исследовании изопериметрической теоремы, которую мы выскажем теперь в следующей форме: Из всех плоских фигур равного периметра наибольшую площадь имеет круг. Это утверждение отличается от утверждения, приведенного выше (§ 2), и не только словесно. Однако мы можем показать, что эти два утверждения равносильны. Мы отложим это доказательство (см. § 8) и поспешим перейти к рассмотрению следствий.

Рис. 10.1. Задача Дидоны.	Рис. 10.2. Решение с помощью зеркального отражения.

(1) Дидона, дочь тирского царя, бежавшая от отца, после многих приключений прибыла на берег Африки, где она позднее стала основательницей Карфагена и его первой легендарной царицей. Дидона начала с того, что купила у туземцев участок земли на берегу моря «не больше, чем можно окружить воловьей шкурой». Она разрезала воловью шкуру на тонкие узкие полосы, из которых связала очень длинную веревку. А затем Дидона столкнулась с геометрической задачей: участок земли какой формы следовало бы окружить ее веревкой данной длины, чтобы получить наибольшую площадь?

Во внутренней части континента ответ давал бы, конечно, круг, но на берегу моря задача изменяется. Решим ее в предположении, что берег представляет собой прямую линию. На рис. 10.1 дуга XYZ имеет данную длину. Требуется сделать максимальной площадь между этой дугой и прямолинейным отрезком XZ (который лежит на данной бесконечной прямой, но по желанию может быть удлинен или укорочен).

Чтобы решить эту задачу, рассмотрим данную бесконечную прямую (берег моря) как зеркало; см. рис. 10.2. Линия XYZ и ее

190

зеркальное отражение XYZY′ совместно образуют замкнутую кривую XYZY′ данной длины, окружающую лошадь, которая в точности вдвое больше площади, максимум которой нам нужно найти. Эта площадь максимальна, когда замкнутая кривая — окружность, для которой данная бесконечная прямая (берег моря) является осью симметрии. Следовательно, решение задачи Дидоны — полукруг с центром на берегу моря.

Рис. 10.3. Вписанный многоугольник.	Рис. 10.4. Гибкие суставы и картонные сегменты.

(2) Якоб Штейнер вывел из изопериметрической теоремы множество интересных следствий. Разберем одно из его рассуждений, являющееся особенно поразительным. Впишем в данный круг многоугольник (рис. 10.3). Сегменты круга (заштрихованные на рис. 10.3), отсекаемые сторонами вписанного многоугольника, будем рассматривать как жесткие (вырезанные из картона). Представим себе, что эти жесткие сегменты круга в вершинах вписанного многоугольника соединены гибкими суставами. Продеформируем эту суставчатую систему, изменяя углы в суставах. После деформации (см. рис. 10.4) мы получим новую кривую, которая не является окружностью, но состоит из следующих одна за другой дуг окружности и имеет ту же длину, что и данная окружность. Поэтому в силу изопериметрической теоремы площадь, ограниченная новой кривой, должна быть меньше, чем площадь данного круга. Однако сегменты круга жесткие (из картона), их площади не изменились и, таким образом, площадь уменьшилась за счет деформированного многоугольника. Площадь вписанного в круг многоугольника больше, чем площадь любого другого многоугольника с такими же сторонами (стороны одинаковы по длине и по порядку следования).

Это следствие изящно, но пока не доказано, поскольку мы пока не доказали саму изопериметрическую теорему.

(3) Соединим задачу Дидоны с методом Штейнера. Впишем в данный полукруг ломаную линию; см. рис. 10.5. Сегменты, отсекаемые

191

от полукруга звеньями ломаной линии (заштрихованные на рис. 10.5), будем рассматривать как жесткие (из картона). Поместим в вершины ломаной гибкие суставы, изменим углы и переместим концы ломаной, но содержащей диаметр, прямой, которую мы рассматриваем как заданную. Так мы получим новую кривую (рис. 10.6), состоящую из дуг окружности той же общей длины, что и полуокружность, но в силу теоремы, которую мы разобрали в (1), заключающую вместе с данной бесконечной прямой площадь меньшую, чем площадь полукруга. Но сегменты круга жесткие (из картона), и поэтому площадь уменьшилась за счет деформированного многоугольника. Отсюда теорема: Даны по длине и порядку следования стороны многоугольника, за исключением одной стороны. Площадь становится наибольшей, когда многоугольник вписан в полукруг, диаметром которого является первоначально не заданная сторона.

Рис. 19.5. Дидона и Штейнер.	Рис. 10.6. Сегменты из картона.

6. Подтверждение следствий. Физик, выведя из своего предположения различные следствия, разыскивает такое следствие, которое можно удобно проверить с помощью экспериментов. Если эксперименты явно противоречат выведенному из него следствию, то подрывается само предположение. Если эксперименты подтверждают следствия, то вес предположения возрастает, оно становится более правдоподобным. Математика может идти подобным же путем. Он[72] разыскивает доступные следствия своего предположения, которые он мог бы доказать или опровергнуть. Опровергнутое следствие опровергает само предположение. Показанное следствие делает предположение более правдоподобным и может подсказать путь, на котором удалось бы доказать само предположение.

Как обстоит дело с нашим случаем? Мы вывели из изопериметрической теоремы несколько следствий; какое из них является наиболее доступным?

(1) Некоторые из следствий, выведенных в предыдущем параграфе из изопериметрической теоремы, в действительности относятся к элементарным задачам на максимум. Имеется ли какое-нибудь следствие, которое мы могли бы подтвердить? Просмотрим различные случаи, указанные рис. 10.3 — 10.6. Какой из них самый простой? Сложность многоугольника возрастает с увеличением числа его сторон. Следовательно, простейшим из всех многоугольников является треугольник;

192

конечно, нам больше всего нравится треугольник, потому что мы о нем больше всего знаем. Но задача рис 10.3 и 10.4 для треугольников теряет смысл, или, мы можем сказать, в случае треугольника она бессодержательна: треугольник с заданными сторонами является определенным, жестким. Для треугольника нет никакого перехода, подобного переходу от рис. 10.3 к рис. 10.4. Однако переход от рис. 10.5 к рис. 10.6 для треугольников вполне возможен. Это, пожалуй, самое простое следствие, выведенное нами до сих пор из изопериметрической теоремы; исследуем его.

Простейший частный случай результата, выведенного в § 5(3), решает следующую задачу: Даны две стороны треугольника; найти максимум его площади; см. рис. 10.7. Ответ получен в § 5 (3): площадь наибольшая, когда треугольник вписан в полукруг, диаметром которого служит первоначально незаданная сторона. Это, однако, означает, что площадь наибольшая, когда две данные стороны заключают прямой угол, что очевидно (пример 8.7).

Рис. 10.7. Палец с одним суставом.	Рис. 10.8. Сверхпалец.

Нам удалось подтвердить первое следствие изопериметрической теоремы. Такая удача, естественно, поднимает наше настроение. Что кроется за только что подтвержденным фактом? Не могли бы мы подтвердить какое-нибудь другое следствие?

(2) Обобщая задачу, рассмотренную в (1), приходим к следующей задаче: Даны величины всех последовательных сторон многоугольника, за исключением одной. Найти максимум площади.

Введем подходящие обозначения и начертим рис. 10.8. Длины сторон AB, BC, …, KL заданы; длина стороны LA не задана. Мы можем представлять себе ломаную линию ABC… F … KL. как своего рода «сверхпалец»: «кости» AB, BC, …, KL имеют постоянную длину, углы в суставах B, C, ..., F; ..., K переменны. Требуется сделать площадь ABC … KLA максимальной.

Как и в некоторых задачах, рассмотренных нами ранее (§§ 8.4 и 8.5), характерная трудность, по-видимому, состоит в том, что переменных много (углы в B, C, …, F, … и K). Однако только что, в (1), мы рассмотрели крайний частный случай задачи, когда имеется всего лишь один переменный угол (один лишь сустав; рис 10.7). Естественно надеяться, что мы сможем воспользоваться этим частным случаем как точкой опоры для решения общей задачи.

193

Действительно, рассмотрим задачу как почти решенную. Представим себе, что мы уже получили искомые значения всех углов, за исключением одного. На рис. 10.9 мы считаем угол в F переменным, но все другие углы, в B, C, …, K — фиксированными; суставы B, C, …, K — жесткие и только F — гибкий. Соединим A и L с F. Едины AF и LF постоянны. Весь многоугольник ABC… F … KLA разлагается теперь на три части, две из которых жесткие (из картона) и только третья может изменяться. Многоугольники ABC… FA и LK … FL жесткие. Треугольник AFL имеет две данных стороны, FA и FL, и переменный угол в F ABC… F … KLA. Площадь этого треугольника и с ней площадь всего многоугольника ABC… F … KLA становится максимальной, когда ∠AFL является прямым углом, как мы только что сказали в (1), рассматривая на рис. 10.7.[73]

Рис. 10.9. Только один сустав гибкий.

Это рассуждение, очевидно, в такой же степени применимо и к другим суставам, т. е. к углам в B, C, … и K (рис. 10.8), и, таким образом, мы видим: площадь многоугольника ABC… KLA не может быть максимальной, если первоначально не заданная сторона AL не стягивает в каждой из вершин, не принадлежащих к ней, в B, C, …, F,…, K, прямой угол. Если наибольшая площадь существует, то она должна достигаться в только что описанной ситуации. То, что наибольшая площадь существует, мы можем считать не требующим доказательства и, немножко вспоминая элементарную геометрию, следующим образом можем описать эту ситуацию в других выражениях: максимум площади достигается в том и только в том случае, если многоугольник вписан в полукруг, диаметром которого является первоначально не заданная сторона.

Мы получили в точности тот же результат, что и в 9 5(3), но здесь мы не пользовались изопериметрической теоремой, а там пользовались.

(3) Сначала, в (1), мы подтвердили очень специальное следствие изопериметрической теоремы, затем, в (2), значительно более широкое следствие. Мы развили теперь, пожалуй, достаточную скорость, чтобы взяться за другое широкое следствие, выведенное выше, в § 5(2).

Сравним два многоугольника ABC… KL и A′B′C′… K′L′; см. рис 10.10. Соответствующие стороны равны, AB = A′B′, BC = B′C′, …, KL = K′L′, LA = L′A′, но некоторые углы различны; ABC… KL вписан в круг, а A′B′C′… K′L′ — нет.

Соединим вершину J многоугольника ABC… KL с центром описанной окружности и проведен диаметр JM. Если случайно точка M совпадет с вершиной многоугольника ABC… KL, наша задача

194

значительно упростится [мы могли бы в этом случае немедленно воспользоваться результатом, полученным в (2)]. Если нет, то M лежит на окружности между двумя соседними вершинами вписанного многоугольника, скажем, A и B. Проведем MA, MB, рассмотрим ∆AMB (заштрихованный на рис. 10.10) и построим ∆A′M′B′ на основании A′B′ (также заштрихованный), равный ∆AMB, Наконец проведем J′M′.

Рис. 10.10. Один многоугольник вписан, другой нет.

Многоугольник AMBC … KL делится прямой JM на две части (см. рис. 10.10); многоугольник A′M′B′C′… K′L′ соответствующим образом делится прямой J′M′. Применим к обеим частям теорему, доказанную в (2). Площадь многоугольника MBC … J, вписанного в полукруг, не меньше, чем площадь многоугольника M′B′C′ … J′; действительно, все соответствующие стороны, за исключением MJ и M′J′, равны, и лишь сторона MJ, образующая диаметр полукруга, может отличаться от M′J′. По той же причине площадь многоугольника MALK … J не меньше, чем площадь M′A′L′K′ … J. Складывая, получаем, что

площадь AMBC … KL > площади A′M′B′C′ … K′L′.

Однако

∆AMB = ∆ A′M′B′.

Вычитая, получаем, что

площадь ABC … KL > площади A′B′C′ … K′L′.

Площадь многоугольника, вписанного в круг, больше, чем площадь любого другого многоугольника с такими же сторонами.

Мы получили здесь в точности тот же результат, что и в § 5(2), но здесь мы не пользовались нзопериметрической теоремой, а там пользовались.

(Первое неравенство между площадями сложенных многоугольников содержит знак >, хотя добросовестный читатель мог ожидать знак ≥. Рассмотрим этот несколько более тонкий пункт. Я утверждаю,

195

что многоугольник A′M′B′C′ … K′L′ не может быть вписан в круг; в противном случае A′B′C′ … K′L′ также можно было бы вписать в круг, что неверно. Я утверждаю, что оба многоугольника M′B′C′ … J′ и M′A′L′K′ … J нельзя вписать в полукруг с диаметром M′J′; в противном случае весь многоугольник A′M′B′C′ … K′L′ можно было бы вписать в круг, что неверно. Поэтому слова «не меньше», дважды употребленные при выводе рассматриваемого неравенства, по крайней мере один раз можно заменить словом «больше»[64]).

7. Очень близко[74]. Следствия, которые нам удалось подтвердить, делают изопериметрическую теорему чрезвычайно правдоподобной. Больше того, у нас, возможно, появилось чувство, что эти следствия «многое содержат», что мы «очень близки» к окончательному решению, к полному доказательству.

(1) Найти многоугольник с данным числом сторон и данным периметром, имеющий наибольшую площадь.

Если такой многоугольник существует, то он должен быть вписанным в круг. Эго мы можем непосредственно заключить из нашего последнего замечания, § 6(3).

С другой стороны, рассмотрим задачу как почти решенную. Допустим, что мы уже знаем правильные положения всех вершин, за исключением одной, скажем X. Другие n — 1 вершин, скажем U… V, Y и Z, уже фиксированы. Весь многоугольник U… WXYZ состоит из двух частей: многоугольника U… WYZ с n — 1 уже фиксированными вершинами, который не зависит от X, и ∆WXY, зависящего от X. У этого треугольника, ∆WXY, мы знаем основание WY и сумму двух других сторон WX + XY; в самом деле, остающиеся n — 2 стороны многоугольника предполагаются известными, а мы в действительности знаем сумму всех n сторон. Площадь ∆WXY должна быть наибольшей. Однако почти очевидно, что площадь ∆WXY с известным основанием и периметром достигает своего максимума, когда треугольник является равнобедренным (пример 8.8). Таким образом, WX = XY; две смежные стороны искомого многоугольника равны. Поэтому (в силу симметрии условий и схемы частного изменения) любые две смежные стороны равны. Все стороны равны: искомый многоугольник является равносторонним.

Искомый многоугольник, вписанный в круг, а также равносторонний, необходимо является правильным: Из всех многоугольников с данным числом сторон и данным периметром наибольшую площадь имеет правильный многоугольник.

(2) Два правильных многоугольника, один с n, а другой с n + 1 сторонами, имеют один и тот же периметр. Какой имеет бо́льшую площадь?

196

Правильный многоугольник с n + 1 сторонами, как мы только что [в (1)] видели, имеет площадь бо́льшую, чем неправильный многоугольник с n + 1 стороной и тем же периметром. Но правильный многоугольник с n сторонами, каждая из которых равна, скажем, a, можно рассматривать как неправильный многоугольник с n + 1 сторонами, имеющий n — 1 сторон длины a, две стороны длины a /2 и один угол, равный 180°. (Середину одной стороны многоугольника, понимаемого обычным образом, считайте вершиной, и тогда вы придете к этому менее привычному пониманию.) Итак, правильный многоугольник с n + 1 сторонами имеет бо́льшую площадь, чем правильный многоугольник с n сторонами и тем же периметром.

(3) Круг и правильный многоугольник имеют один и тот же периметр. Что имеет бо́льшую площадь?

Продумаем, что означает полученный в (2) результат. Возьмем n = 3, 4, … и сформулируем результат в каждом частном случае. Переходя от равностороннего треугольника к квадрату с тем же периметром, мы находим, что площадь возросла. Переходя от квадрата к правильному пятиугольнику с тем же периметром, вновь находим, что площадь возросла. И так далее, переходя от одного правильного многоугольника к следующему, от пятиугольника к шестиугольнику, от шестиугольника к семиугольнику, от n к n + 1, мы видим, что площадь с каждым шагом возрастает, когда периметр остается неизменным. В конечном счете в пределе мы получаем круг. Его периметр все еще тот же, но его площадь, очевидно, превосходит площадь любого правильного многоугольника, пределом бесконечной последовательности которых он является. Площадь круга больше, чем площадь любого правильного многоугольника с тем же периметром.

(4) Круг и произвольный многоугольник имеют один и тот же периметр. Что имеет бо́льшую площадь?

Круг. Это немедленно следует из (1) и (3).

(5) Круг и произвольная фигура имеют один и тот же периметр. Что имеет бо́льшую площадь?

Круг. Это следует из (4), так как любая фигура является пределом многоугольников. Мы доказали изопериметрическую теорему!

8. Три формы изопериметрической теоремы. В предыдущих параграфах (§ 6 и 7) мы доказали изопериметрическую теорему в следующей формулировке:

I. Из всех плоских фигур равного периметра наибольшую площадь имеет круг.

Однако в § 2 мы рассматривали другую формулировку:

II. Из всех плоских фигур равной площади наименьший периметр имеет круг.

Эти две формулировки различны и различны не только словесно. Они нуждаются в некотором дальнейшем объяснении.

197

(1) Две фигуры называются «изопериметрическими», если их периметры равны. «Из всех изопериметрических плоских фигур наибольшую площадь имеет круг» — вот традиционная редакция формулировки I, которая объясняет название «изопериметрическая теорема».

(2) Мы можем называть эти две формулировки теоремы (I и II) «сопряженными формулировками» (см. § 8.6). Мы докажем, что эти два сопряженных утверждения равносильны одно другому, показав, что оба они равносильны одному и тому же третьему.

(3) Пусть A обозначает площадь, а L — длину периметра данной фигуры. Допустим, что данная фигура и круг радиуса r являются изопериметрическими: L = 2πr. Тогда первая форма изопериметрической теоремы (формулировка I) утверждает, что

A ≤ πr.

Подставляя вместо r его выражение через L, r = L/2π, легко преобразуем неравенство:

Назовем это неравенство изопериметрическим неравенством, а частное в левой части — изопериметрическим частным. Это частное зависит только от формы фигуры и не зависит от ее размеров. Действительно, если, не изменяя формы, мы увеличим линейные размеры фигуры в отношении 1 : 2, то периметр станет равен 2L, а площадь — 4A, но частное A/L² останется неизменным, и это же верно для 4πA/L² и для увеличения в любом отношении. Некоторые авторы называют изопериметрическим частным A/L²; мы ввели множитель 4π, чтобы сделать наше изопериметрическое частное в случае круга равным 1. В этой терминологии мы можем сказать:

III. Из всех плоских фигур наибольшее изопериметрическое частное имеет круг[65].

Это третья форма изопериметрической теоремы.

(4) Мы пришли к третьей форме теоремы, отправляясь от фигур с равным периметром. Теперь начнем с утверждения III и перейдем к фигурам с равной площадью. Допустим, что фигура с площадью A и периметром L имеет ту же площадь, что и круг радиуса r , т. е. A = πr². Подставляя вместо A это выражение, легко преобразовать изопериметрическое неравенство в L ≥ 2πr. Это означает, что периметр этой фигуры больше, чем периметр круга с равной площадью. Мы пришли ко второй сопряженной форме теоремы, к утверждению II.

(5) Мы могли бы, конечно, провести это рассуждение в обратном направлении и, переходя через III, из II вывести I. И, таким образом, мы можем убедиться, что все три формы равносильны.

198

9, Приложения и вопросы. Если Дидона заключила с туземцами сделку в окрестности мыса, то ее задача была, пожалуй, больше похожа не на рассмотренную в § 5 (1), а на следующую:

Дан угол (бесконечная часть плоскости между двумя лучами, проведенными из одной и той же начальной точки). Найти наибольшую площадь, отсекаемую от него линией данной длины.

На рис. 10.11 вершина данного угла обозначена буквой М (мыс). Предполагается, что произвольная линия, соединяющая точки X и Y, имеет данную длину l. Требуется сделать максимальной треугольную площадь между этой кривой и берегом моря. Мы можем передвигать концы Х и У кривой и видоизменять ее форму, но не можем изменять ее длину l.

Рис. 10.11. Задача Дидоны, усложненная мысом.	Рис. 10.12. Иногда ее решают отражения.

Задача не слишком легка, но является одной из тех задач, которые частный выбор данных делает более доступными. Если угол в М прямой, то мы можем взять зеркальное отражение фигуры сначала относительно одной стороны угла, а затем относительно другой. Мы получим таким образом новую фигуру, рис. 10.12, и новую задачу. Линия XY, учетверенная отражениями, дает новую замкнутую линию данной длины 4l. Площадь, максимум которой нужно найти, учетверенная отображениями, дает новую площадь, целиком окруженную новой данной кривой, и нужно найти максимум этой новой площади. В силу изопериметрической теоремы решением новой задачи служит круг. Этот круг имеет две данные оси симметрии, XX′ и YY′, и, таким образом, его центр находится в точке пересечения этих двух осей, в точке М. Следовательно, решением первоначальной задачи (задачи Дидоны) является квадрант: четверть круга с центром в вершине данного угла.

Мы, естественно, вспоминаем здесь решение задачи из § 5(1), основанное на рис. 10.2, и замечаем, что оно совершенно аналогично настоящему решению. Легко видеть, что существует бесконечное множество дальнейших частных случаев, в которых годится этого рода решение. Если данный угол в М равен 360°/2n =180°/n, то

199

мы можем с помощью повторных отражений преобразовать кривую XY данной длины l в новую замкнутую кривую длины 2nl, а предложенную задачу в новую задачу, решением которой в силу изопериметрической теоремы будет круг. Случаи, разобранные в § 5(1) и в настоящем параграфе, как раз являются в этой бесконечной последовательности первыми двумя случаями, соответствующими n =1 и 2.

Таким образом, если угол с вершиной в М имеет специальный вид (180°/n при целом n), то решением нашей задачи (рис. 10.11) будет дуга окружности с центром в М. Естественно ожидать, что эта форма решения не зависит от величины угла (по крайней мере пока он не превышает 180°), Таким образом, мы делаем предположение, что решением задачи рис. 10.11, независимо от того, имеет ли угол с вершиной в М специальный вид 180°/n или нет, является дуга окружности с центром в М. Это предположение есть индуктивное предположение, подкрепленное в бесконечном множестве случаев, n = 1, 2, 3, ..., доказательством. Верно ли это предположение?

Рассмотренное приложение изопериметрической теоремы и связанный с ним вопрос могут побудить нас ожидать много подобных же приложений и вопросов. Наш вывод теоремы поднимает дальнейшие вопросы; ее аналоги в пространственной геометрии и математической физике подсказывают новые вопросы. Изопериметрическая теорема, глубоко коренящаяся в нашем опыте и интуиции, которую так легко предположить, но не так легко доказать, служит неисчерпаемым источником вдохновения.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ X

Первая часть

1. Взгляд назад. В предыдущих параграфах (§§ 6—8) мы доказали изопериметрическую теорему — доказали ли? Проверим рассуждение шаг за шагом.

По-видимому, нет возражений против простого результата § 6 (1). Однако при решении задачи в § 6 (2) мы без доказательства допустили существование максимума; и это же мы сделали в § 7 (1). Не лишают ли силы наш результат эти недоказанные допущения?

2. Могли бы вы вывести какую-либо часть этого результата иначе? Непосредственно убедитесь в том, что верен простейший нетривиальный частный случай результата, найденного в § 5 (2), т, е. независимо от § 6 (3) докажите, что площадь четырехугольника, вписанного в круг, больше, чем площадь любого другого четырехугольника с такими же сторонами. (Пример 8.41.)

3. Заново с большими подробностями проведите рассуждение из § 7 (2): постройте многоугольник с n + 1 сторонами, имеющий тот же периметр, что и правильный многоугольник с и сторонами, но бо́льшую площадь.

4. Докажите независимо от § 7(3), что круг имеет бо́льшую площадь, чем правильный многоугольник с тем же периметром.

5. Докажите более общее утверждение, что круг имеет бо́льшую площадь, чем многоугольник с тем же периметром, в который можно вписать окружность.

6. Заново, с бо́льшими подробностями, проведите рассуждение из § 7 (6). Доказывает ли оно утверждение I § 8? Есть ли какое-нибудь возражение?

7. Можете ли вы воспользоваться этим нападая для решения какой-нибудь другой эадачи2 Воспользуйтесь методом 3 8, чтобы доказать, что равносильны следующие два утверждения:

200

«Из всех ящиков с данной площадью поверхности наибольший объем имеет куб».

«Из всех ящиков с данным объемом наименьшую площадь поверхности имеет куб».

8. Более сильная форма изопериметрической теоремы. Сравните утверждения, I, II, III § 8 со следующими.

I′. Площадь круга больше, чем площадь любой другой плоской фигуры с тем же периметром.

II′. Периметр круга меньше, чем периметр любой другой плоской фигуры с той же площадью.

III′. Если A — площадь плоской фигуры, а L — ее периметр, то

и равенство достигается в том и только в том случае, если эта фигура — круг.

Покажите, что I′, II′ и III′ между собой равносильны. Доказали ли мы I′?

9. Дана фигура C с периметром L и площадью A; C не является кругом. Постройте фигуру C′ с тем же периметром L, но с площадью A′, большей чем A.

Эта задача важна (почему?), но не слишком легка. Если вы не можете решить ее в полной общности, то решите ее в существенных частных случаях; поставьте уместные вопросы, которые могут подвести вас ближе к ее общему решению; попытайтесь заново ее сформулировать; попытайтесь подойти к ней с той или иной стороны.

10. Даны четырехугольник C с входящим углом, его периметр L и площадь A. Постройте треугольник C′ с тем же периметром C, но с площадью A′, большей чем A.

11. Обобщите пример 10.

12. Информация «C не есть круг» является «чисто отрицательной». Могли бы вы охарактеризовать C более «положительно» каким-нибудь способом, который дал бы вам точку опоры для того, чтобы взяться за решение примера 9?

[Любые три точки произвольной кривой лежат на одной окружности или на одной прямой. Что можно сказать о четырех точках?]

13. Дана фигура C с периметром L и площадью A; на кривой, ограничивающей фигуру C, существуют четыре точки P, Q, R и S, не лежащие ни на одной окружности, ни на одной прямой. Постройте фигуру C′ с тем же периметром L, но с площадью A′, большей чем A. [Пример 2.]

14. Сравните следующие два вопроса.

Рассмотрим фигуры с данным периметром. Если C — такая фигура, но не круг, то мы можем построить другую фигуру C′ с большей площадью. (Действительно, это сделано в примерах 10 — 13. Условие, что C не круг, существенно; наше построение не увеличивает площади круга.) Можем ли мы отсюда заключить, что круг имеет наибольшую площадь?

Рассмотрим положительные целые числа. Если n — такое число, но не 1, то мы можем построить другое целое число n′, большее чем n. (Действительно, положим n′ = n². Условие n > 1 существенно; наше построение не годится для n = 1, так как 1² = 1.) Можем ли мы отсюда заключить, что 1 — наибольшее целое число?

Укажите отличие, если оно существует.

15. Докажите утверждение I′ примера 8.

Вторая часть

16. Палка и веревка. Даны палка и веревка; каждый конец веревки (которая, конечно, должна быть длиннее палки) привязан к соответствующему концу палки. Окружите этим устройством наибольшую возможную площадь.

Положите палку. Ее концы A и B полностью определяют ее положение. Однако веревка может принимать бесконечно много форм, образуя произволь-

201

ную кривую данной длины, начинающуюся в A и кончающуюся в B; см. рис. 10.13. Одной из возможных форм веревки является дуга окружности, заключающая вместе с палкой круговой сегмент. Дополните круг, добавив другой сегмент (заштрихованный на рис. 10.14, I), и этот же сегмент прибавьте к фигуре, образованной палкой и произвольным положением веревки (рис. 10.14, II). Круг I рис. 10.14 имеет бо́льшую площадь, чем любая другая фигура с тем же периметром, а II на рис. 10.14 и есть такая фигура. Вычитая один и тот же (заштрихованный) сегмент из I и II, находим результат: площадь, окруженная палкой и веревкой, будет наибольшей, когда веревка образует дугу окружности.

Рис. 10.13. Палка и веревка.

Этот результат остается справедливым, если мы прибавим к переменной площади на рис. 10.13 по ее постоянной прямой граничной линии любую постоянную площадь. Это замечание оказывается полезным.

Выскажите сопряженный результат, т. е. сформулируйте факт, который имеет такое же отношение к теореме II § 8, какое только что найденный факт имеет к теореме I § 8.

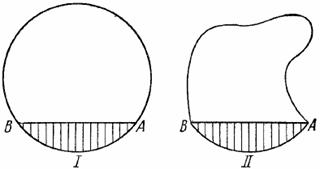
Рис. 10.14. Принцип дуги окружности.

17. Дан угол (бесконечная часть плоскости между двумя лучами, проведенными из одной и той же начальной точки) и две точки, по одной на каждой стороне угла. Найдите наибольшую площадь, отсекаемую от угла линией данной длины, соединяющей две данные точки. (На рис. 10.11 точки X и Y заданы.)

18. Дан угол, меньший чем 180°, и точка на одной из его сторон. Найдите наибольшую площадь, отсекаемую от угла линией данной длины, начинающейся в данной точке. (На рис. 10.11 точка X задана, но точка Y является переменной.)

19. Дан угол, меньший чем 180°. Найдите наибольшую площадь, отсекаемую от угла линией данной длины. (На рис. 10.11 точки X и Y являются переменными. Предположение было высказано в § 9.)

20. Дан угол, меньший чем 180°. Найдите наибольшую площадь, отсекаемую от угла прямолинейным отрезком данной длины.

21. Две палки и две веревки. Имеем две палки: AB и CD. Первая веревка привязана к последней точке B первой палки одним юнцом и к первой точке C второй палки другим концом. Вторая веревка подобным же образом связывает D и A. Окружите этим устройством наибольшую возможную площадь.

22. Обобщите.

23. Перейдите к частному случаю и таким путем получите элементарную теорему, игравшую в этой главе важную роль.

202

24. Дана окружность в пространстве. Найдите поверхность с данной площадью, ограниченную данной окружностью и заключающую вместе с кругом, ограниченным данной окружностью, наибольший объем. [Знаете ли вы какую-нибудь аналогичную задачу&)

25. Задача Дидоны в пространственной геометрии. Дан трехгранный угол годна из восьми бесконечных частей, на которые пространство разбивается тремя плоскостями, пересекающимися в одной точке). Найдите наибольший объем, отсекаемый от трехгранного угла поверхностью данной площади.

Эта задача слишком трудна. От вас требуется только выбрать более доступный частный случай.

26. Найдите задачу, аналогичную примеру 25, результат которой вы можете предвидеть. [Обобщите, перейдите к частному случаю, перейдите к пределу, ...]

27. Биссекторы плоской области. Рассмотрим плоскую область, ограниченную некоторой кривой. Дуга, соединяющая две точки граничной кривой, называется биссектором области, если она делит область на две части равной площади.

Покажите, что любые два биссектора одной и той же области имеют по крайней мере одну общую точку.

28. Сравните два биссектора квадрата. Один — прямолинейный отрезок, параллельный одной из сторон и проходящий через центр квадрата. Другой — четверть окружности с центром в вершине квадрата. Какой из них короче?

29. Найдите кратчайший прямолинейный биссектор равностороннего треугольника.

30. Найдите кратчайший биссектор равностороннего треугольника.

31. Покажите, что кратчайшими биссекторами круга являются его диаметры.

32. Найдите кратчайший биссектор эллипса.

33. Попытайтесь сформулировать общие теоремы, охватывающие примеры 28—32.

34. Биссекторы замкнутой поверхности[66]. Замкнутая кривая без самопересечений, лежащая на замкнутой поверхности, называется биссектором этой поверхности, если она делит поверхность на две части (открытые поверхности) равной площади.

Покажите, что любые два биссектора одной и той же поверхности имеют по крайней мере одну общую точку.

35. Кратчайший биссектор поверхности многогранника состоит из кусков, каждый из которых есть или прямолинейный отрезок, или дуга окружности.

36. Кратчайший биссектор поверхности правильного многогранника является правильным многоугольником. Найдите его форму и расположение и число решений для каждого из пяти правильных многогранников. (Можете экспериментировать с моделью многогранника и резиновой лентой.)

37. Покажите, что кратчайшими биссекторами сферы являются большие круги.

38. Попытайтесь найти обобщение примера 37, охватывающее и существенную часть примера 36. [Примеры 9.23, 9,24.]

39. Дан шар S радиуса a. Назовем диафрагмой S ту часть сферической поверхности, пересекающей S, которая находится внутри S[75]. Докажите:

(1) Все диафрагмы, проходящие через центр шара S, имеют одинаковую площадь.

12) Никакая диафрагма, делящая объем шара S пополам, не имеет площади, меньшей чем πa.

Последнее утверждение и рассмотренные аналогичные случаи подсказывают предположение. Сформулируйте его. [Примеры 31, 37.]

203

40. Фигура многих совершенств. Рассмотрим плоскую область, ограниченную некоторой кривой. Мы хотим обозреть некоторые из большого числа теорем, аналогичных изопериметрической теореме: Из всех областей с данной площадью наименьший периметр имеет круг.

Мы уже встречались с одной теоремой этого рода. В § 4 мы рассмотрели некоторые индуктивные доводы в пользу утверждения: Из всех мембран с данной площадью наиболее низкий основной тон издает круглая мембрана,

Рассмотрим теперь область как однородную пластинку постоянной толщины. Рассмотрим момент инерции этой пластинки относительно перпендикулярной к ней оси, проходящей через ее центр тяжести. Этот момент инерции, который мы назовем «полярным моментом инерции», зависит при прочих равных условиях от размера и формы пластинки. Из всех пластинок с данной площадью наименьший полярный момент имеет круглая пластинка.

Эта пластинка, если она является проводником электричества, может также вместить электрический заряд, пропорциональный ее электростатической емкости. Емкость также зависит от размера и формы пластинки. Из всех пластинок с данной площадью наименьшую емкость имеет круглая пластинка.

Пусть теперь область является поперечным сечением однородного упругого бруса. Если мы попытаемся закрутить такой брус вокруг его оси, то сможем заметить, что он сопротивляется скручиванию. Это сопротивление, или «жесткость на кручение» бруса зависит при прочих равных условиях от размера и формы поперечного сечения. Из всех поперечных сечений с данной площадью наибольшую «жесткость на кручение» имеет круглое поперечное сечение[67].

Почему круг является решением такого большого числа таких различных задач на максимум и минимум? В чем «причина»? Не является ли «истинной причиной» «совершенная симметрия» круга? Такие туманные вопросы могут быть стимулирующими и плодотворными, если только вы не просто с удовольствием занимаетесь туманными разговорами и размышлениями, но серьезно пытаетесь спуститься к чему-нибудь более точному или более конкретному.

41. Аналогичный случай. Не видите ли вы аналогии между изопериметрической теоремой и теоремой о средних? (См. § 8.6)

Длина замкнутой кривой одинаково зависит от каждой точки, или от каждого элемента этой кривой. И площадь области, ограниченной кривой, также одинаково зависит от каждой точки, или элемента этой кривой. Мы разыскиваем максимум площади, когда длина задана. Поскольку обе рассматриваемые величины имеют такую природу, что никакая точка кривой не играет в их определении предпочтительной роли, мы не должны удивляться, что решением является единственная такая кривая, которая содержит каждую из своих точек одинаковым образом и любые два элемента которой наложимы один на другой: окружность.

Сумма x₁ + x₂ + … + x_n есть симметрическая функция переменных x₁, x₂, …, x_n т. е. она одинаково зависит от каждой переменной. И произведение x₁x₂… x₂ одинаково зависит от каждой переменной. Мы разыскиваем максимум произведения, когда сумма задана. Поскольку обе рассматриваемые величины являются симметричными относительно n переменных, мы не должны удивляться, что решение требует, чтобы x₁ = x₂ = ... = x_n.

Существуют, кроме площади и длины, и другие величины, зависящие от размеров и формы замкнутой кривой, которые «одинаково зависят от каждого элемента кривой»; несколько таких величин мы перечислили в примере 40. Мы разыскиваем максимум величины этого рода, когда другая величина этого же рода задана. Является ли решение, если оно существует, обязательно окружностью?

204

Для правдоподобного ответа обратимся к простейшему аналогичному случаю. Рассмотрим две симметрические[76] функции f(x₁, x₂, …, x_n) от n переменных и будем разыскивать экстремум функции f(x₁, x₂, …, x_n), когда задано, что g(x₁, x₂, …, x_n) = 1. Существуют случаи, когда нет максимума, другие случаи, когда нет минимума, и третьи случаи, когда нет ни максимума, ни минимума. Условие x₁ = x₂ = ... = x_n играет важную роль[68], но, когда достигается максимум или минимум, оно не обязано удовлетворяться. Имеет место, однако, простой факт. Если

x₁ = a₁, x₂ = a₂, x₃ = a₃, …, x_n = a_n

есть решение, то в силу симметрии функций f и g также и

x₁ = a₂, x₂ = a₁, x₃ = a₃, …, x_n = a_n

является решением. Следовательно, если a₁ ≠ a₂,то существуют по крайней мере два различных решения. Если существует единственное решение (т. е. экстремум достигается и достигается ровно для одной системы значений x₁, x₂, …, x_n), то это решение требует, чтобы x₁ = x₂ = … = х_n.

«Comparaison n’est pas raison»[69] говорят французы. Конечно, такое сравнение, как только что сделанное, не может дать непреложного доказательства, а дает только эвристическое указание. Но мы иногда очень рады получить и таюе указание.

Возьмите в качестве иллюстрации

f(x₁, x₂, …, x_n) = (x₁, x₂, …, x_n)²,

g(x₁, x₂, …, x_n) = (x₁², x₂², …, x_n²)/n,

и найдите экстремум f при условии g = 1, рассмотрев (1) все действительные значения x₁, x₂, …, x_n и (2) только неотрицательные действительные значения этих переменных.

42. Правильные многогранники. Найдите многогранник с данным числом n граней и с данной площадью поверхности, имеющий наибольший объем.

Эта очень трудная задача подсказывается аналогичной задачей § 7 (1), которая подсказывает и предположение: если существует правильный многогранник с n гранями, то он дает наибольший объем. Однако каким бы правдоподобным ни казалось это предположение, в двух случаях из пяти оно оказывается ошибочным. В действительности это предположение

верно для n = 4, 6, 12.

неверно для n = 8, 20.

В чем различие? Попытайтесь подметить какое-нибудь простое геометрическое свойство, отличающее эти два вида правильных многогранников.

43. Индуктивные доводы. Пусть V обозначает объем тела, а S — площадь его поверхности. Сказанное в § 8 (3) по аналогии наводит на мысль рассматривать по определению

как изопериметрическое частное в пространственной геометрии. По аналогии мы можем предположить, что наибольшее изопериметрическое частное имеет шар. Таблица III индуктивно подкрепляет это предположение.

205

Проверьте некоторые из тел, приведенных в табл. III, и добавьте новый материал. В частности, попытайтесь найти тело с изопериметрическим частным, большим чем частное правильного икосаэдра.

Таблица III

Изопериметрическое частное 36πV²/S³

Шар	1,0000
Икосаэдр	0,8288
Наилучший двойной конус	0,7698
Додекаэдр	0,7547
Наилучшая призма	0,6667
Октаэдр	0,6045
Куб	0,5236
Наилучший конус	0,5000
Тетраэдр	0,3023

По поводу терминов «наилучшие» двойной конус, призма и конус см. соответственно примеры 8.38, 8.35 и 8.52.

XI. ДРУГИЕ ВИДЫ ПРАВДОПОДОБНЫХ ДОВОДОВ

Индукция основывается на том, что простейшие отношения суть самые обыкновенные. — Лаплас[70]

1. Предположения и предположения. Все наши предыдущие рассмотрения были посвящены выяснению роли предположений в математическом исследовании. Наши примеры дали нам возможность познакомиться с двумя видами правдоподобных аргументов, говорящих за или против высказанного предположения: мы рассмотрели индуктивные аргументы, основанные на подтверждении следствий, и аргументы, основанные на аналогии. Существуют ли другие виды полезных правдоподобных аргументов за или против предположения? Примеры настоящей главы имеют целью выяснить этот вопрос.

Нам следует также ясно понять, что существуют предположения различных видов: большие и малые, оригинальные и обычные предположения. Существуют предположения, сыгравшие яркую роль в истории науки, но и решение наиболее скромной математической задачи может нуждаться в каком-нибудь соответственно скромном предположении или догадке. Мы начнем с примеров из классной комнаты, а затем перейдем к другим примерам, имеющим историческое значение.

2. Суждение по родственному случаю. Работая над задачей, мы часто пытаемся догадаться. Конечно, нам хотелось бы отгадать полное решение. Если, однако, это нам не удается, мы бываем вполне удовлетворены, когда можем отгадать ту или иную деталь решения. По крайней мере нам хотелось бы знать, является ли наша задача «разумной». Мы спрашиваем себя: Разумна ли наша задача? Можно ли удовлетворить условию? Достаточно ли условие для определения неизвестного? Или недостаточно? Или чрезмерно? Или противоречиво?[71]

Такие вопросы возникают естественно и являются особенно полезными на ранней стадии нашей работы, когда они нуждаются не в окончательном ответе, а только в предварительном ответе, догадке,

207

и бывают случаи, когда мы можем отгадать ответ вполне разумно и с очень небольшими усилиями.

В качестве иллюстрации рассмотрим элементарную задачу пространственной геометрии. Ось цилиндра проходит через центр шара. Поверхность цилиндра пересекает поверхность шара и делит шар на две части: «продырявленный шар» и «пробку». Первая часть расположена вне цилиндра, вторая — внутри. См. фигуру на рис. 11.1, которую нужно было бы вращать вокруг вертикальной прямой AB. Даны радиус шара r и высота цилиндрического отверстия h. Найти объем продырявленного шара.

Знакомясь с предложенной задачей, вполне естественно приходим к обычным вопросам: Достаточны ли данные для определения неизвестного? Или они недостаточны? Или чрезмерны? Данные r и h кажутся как раз достаточными. Действительно, r определяет размер шара, а h — размер цилиндрического отверстия. Зная r и h, мы можем определить продырявленный шар по форме и размеру, и, с другой стороны, для его определения нам нужны r и h.

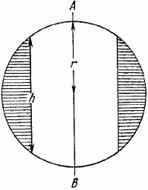
Рис. 111 Продырявленный шар.

Однако, вычисляя искомый объем, мы находим, что он равен πh³/6; см. пример 5. Этот результат кажется крайне парадоксальным. Мы убедились в том, что для определения формы и размеров продырявленного шара нам нужны и r, и h, а теперь оказалось, что для определения его объема r нам не нужно; это звучит совершенно неправдоподобно.

Тем не менее здесь нет противоречия. Если h остается постоянным, а r возрастает, то продырявленный шар заметно изменяется по форме: он становится шире (что ведет к увеличению объема), но его внешняя поверхность становится более плоской (что ведет к уменьшению объема). Мы только не предвидели (и это a priori кажется довольно невероятным), что эти две тенденции в точности уравновешиваются, и объем остается неизменным.

Чтобы понять и этот частный случай, и лежащую в его основании общую идею, мы должны отделить одну от другой разные задачи. Нам следует ясно различать две родственные, но не одинаковые задачи. Если даны r и h, то от нас может требоваться определить

(a) объем и

(b) форму и размер продырявленного шара. Нашей первоначальной задачей было (a). Мы интуитивно видели, что задание r и h и необходимо и достаточно для решения (b). Отсюда следует, что этих данных достаточно и для

208

решения (a), но не следует, что они необходимы для решения (a); и на самом деле они не необходимы.

Отвечая на вопрос: «Необходимы ли эти данные?» мы судили по родственному случаю, вместо (a) подставили (b), мы игнорировали различие между первоначальной задачей (a) и видоизмененной задачей (b). С эвристической точки зрения такое игнорирование может быть оправдано. Нам нужен был только предположительный, но быстрый ответ. Кроме того, такое различие обычно игнорируется: данные, которые необходимы для определения формы и размеров, обычно необходимы и для определения объема. Мы пришли к парадоксу, забыв, что наше заключение было только эвристическим, или как-то неясно веря, что необычное никогда не может случиться. A в нашем примере как раз и случилось необычное.

Суждение о предложенной задаче по видоизмененной задаче — оправданный, разумный эвристический прием. Мы не должны, однако, забывать, что заключение, к которому мы с помощью такого приема приходим, является только предположительным, не окончательным; только правдоподобным, но отнюдь не безусловно верным.

3. Суждение по общему случаю. Следующая задача может быть подходящим образом изложена в классе алгебры для начинающих.

Завещание одного отца трем сыновьям содержит следующие распоряжения.

«Часть моего старшего сына будет равна среднему частей двух других сыновей и трем тысячам долларов. Часть моего второго сына должна быть в точности равна среднему частей двух других. Часть моего младшего сына будет равна среднему двух других без трех тысяч долларов». Каковы эти части?

Достаточно ли условие для определения неизвестных? Имеются достаточные основания сказать да. Действительно, имеются три неизвестных — соответственно части старшего, среднего и младшего сыновей, скажем x, y и z. Каждое из трех приведенных из завещания предложений может быть переведено в уравнение. Далее, вообще говоря, система трех уравнений с тремя неизвестными определяет эти неизвестные. Таким образом, мы совершенно разумно приходим к мысли, что условие предлагаемой задачи достаточно для определения неизвестных.

Выписав, однако, эти уравнения, получаем следующую систему:

209

Складывая эти три уравнения, получаем

x + y + z = x + y + z,

или

0 = 0.

Поэтому любое уравнение этой системы является следствием двух других уравнений. Наша система содержит только два независимых уравнения и, следовательно, на самом деле недостаточна для определения неизвестных.

Задача существенно изменяется, если завещание содержит также и следующее распоряжение: «Я делю все мое состояние, состоящее из 15 000 долларов, между моими тремя сыновьями. Это распоряжение прибавляет к написанной выше системе уравнение

x + y + z = 15 000.

Мы имеем теперь более широкую систему из четырех уравнений. Но, вообще говоря, система из четырех уравнений с тремя неизвестными противоречива. На самом же деле, однако, наша система не противоречива, а как раз достаточна для определения неизвестных, и она дает

x = 7000, y = 5000, z = 3000.

Из кажущихся противоречий этого не слишком глубокого примера не так уж трудно выпутаться, но тщательное объяснение может оказаться полезным.

Неверно, что «система n уравнений с n неизвестными определяет неизвестные». В самом деле, мы только что видели противоречащий пример при n = 3. То, о чем здесь идет речь, является, однако, не математической теоремой, а эвристическим утверждением, в действительности следующим утверждением: «Система n уравнений с n неизвестными, вообще говоря, определяет неизвестные». Слова «вообще говоря» можно понимать по-разному. Здесь речь идет о несколько туманном и грубом «практическом» истолковании: утверждение имеет место «вообще говоря», если оно имеет место «в огромном большинстве таких случаев, которые, вероятно, должны естественно встретиться».

Собираясь решить геометрическую или физическую задачу с помощью алгебры, мы интуитивно пытаемся выразить рассматриваемое условие уравнениями. Каждый пункт этого условия мы пытаемся выразить каким-либо уравнением и стараемся исчерпать таким путем все условие. Если нам удается набрать столько уравнений, сколько у нас неизвестных, то мы надеемся, что сумеем определить эти неизвестные. Такая надежда разумна. Наши уравнения «встретились естественно»; мы можем ожидать, что находимся «в общем случае» Однако пример этого параграфа как раз не встретился естественно,

210

он был специально придуман, чтобы выявить, что в эвристическом утверждении нет абсолютной несомненности. Таким образом, этот пример вовсе не лишает силы лежащий в основании эвристический принцип.

В повседневной жизни мы полагаемся на нечто, что очень необычно. Письма теряются, и поезда терпят крушение, и тем не менее я все еще посылаю письма и без колебания сажусь в поезд. В конце концов потери писем и крушения поездов чрезвычайно необычны; такой несчастный случай происходит только с очень небольшим процентом писем или поездов. Так почему же он должен произойти именно теперь? Подобным же образом, вполне естественно полученные n уравнений с n неизвестными могут оказаться недостаточными для определения неизвестных. Однако, вообще говоря, это не происходит; так почему же это должно произойти именно теперь?

Мы не можем жить и не можем решать задачи, не обладая хотя бы капелькой оптимизма.

4. Более простое предположение предпочтительнее. «Simplex sigillum veri», или «Простота — печать истины», говорили схоластики. Сегодня, когда человечество стало старше и обогатилось значительным научным опытом прошедших веков, нам следовало бы выразиться более осторожно: мы знаем, что истина может быть чрезвычайно сложной. Возможно, схоластики не имели в виду, что простота является необходимой принадлежностью истины; возможно, они намеревались высказать эвристический принцип: «То, что просто, имеет хорошие шансы оказаться истинным». Может быть даже лучше сказать еще меньше и ограничиться плоским советом: «Сначала попробуйте самое простое».

Этот, основанный на здравом смысле совет включает (правда, несколько туманно) эвристические приемы, рассмотренные ранее. То, что объем изменяется, когда изменяется форма, — это не только обычный случай, но и самый простой случай. То, что система n уравнений с n неизвестными определяет неизвестные, — это не только общий случай, но и самый простой случай. Разумно сначала попробовать самый простой случай. Даже если в конечном счете нам придется обратиться к более детальному исследованию более сложных возможностей, предшествующее исследование самого простого случая может послужить полезной подготовкой.

Сначала попробовать самое простое — это часть подхода, который выгоден при встрече с задачами, малыми или большими. Попытаемся представить себе (с значительным упрощением и, несомненно, с некоторым искажением) положение Галилея, когда он исследовал закон падения тел. Если эру современной науки мы хотим исчислять с какой-нибудь определенной даты, то дату этого исследования Галилея можно было бы рассматривать как наиболее подходящую.

211

Нам нужно ясно понять положение Галилея. Он имел нескольких предшественников, нескольких друзей, разделявших его взгляды, но ему решительно противодействовала господствовавшая философская школа, последователи Аристотеля. Эти последователи Аристотеля спрашивали: «Почему тела падают?» — и удовлетворялись каким-то поверхностным, почти чисто словесным объяснением. Галилей спрашивал: «Как тела падают?» — и пытался найти ответ из эксперимента, и притом точный ответ, который можно выразить в числах и математических понятиях. Эта замена «Почему» на «Как», поиски ответа с помощью эксперимента и поиски математического закона, сжато выражающего экспериментальные факты, в современной науке являются общим местом, но во времена Галилея они были революционным нововведением.

Камень, падающий с более высокого места, ударяется о землю сильнее. Баба, падающая из более высокой точки, вбивает сваю глубже в землю. Чем дальше падающее тело от своей начальной точки, тем быстрее оно движется — все это ясно из непосредственного наблюдения. Что самое простое? Кажется, достаточно просто допустить, что скорость тела, начинающего падать из положения покоя, пропорциональна пройденному расстоянию. «Этот принцип выглядит очень естественным, — говорит Галилей, — и он соответствует нашему опыту с машинами, приводимыми в действие с помощью удара». Тем не менее в конечном счете Галилей отверг пропорциональность скорости расстоянию как «не только ошибочную, но и невозможную»[72].

Возражения Галилея против допущения, которое вначале казалось ему таким естественным, могут быть более ясно и отчетливо сформулированы в обозначениях анализа бесконечно малых. Это, конечно, анахронизм; анализ бесконечно малых был открыт после смерти Галилея и, по крайней мере частично, под влиянием его открытий. Тем не менее воспользуемся этим анализом. Пусть t обозначает время, протекшее с момента начала падения, а x — пройденное расстояние. Тогда скорость равна dx/dt (одним из достижений Галилея было то, что он сформулировал отчетливое понятие скорости). Пусть g — подходящая положительная постоянная. Тогда это «самое простое допущение», пропорциональность скорости пройденному расстоянию, выражается дифференциальным уравнением

(1)

Мы должны добавить начальное условие

x = 0, когда t = 0. (2)

212

Из уравнений (1) и (2) следует, что

это условие выражает тот факт, что падающее тело начинает двигаться из положения покоя.

Интегрируя дифференциальное уравнение (1), мы получаем, однако, что

ln x = gt + ln c,

где c — некоторая постоянная. Это дает

Отсюда мы получаем, однако, что

что противоречит (1) и (2): движение, удовлетворяющее дифференциальному уравнению (1), не может начинаться из положения покоя. И, таким образом, предположение, которое казалось таким «естественным», именно «самым простым», на самом деле является внутренне противоречивым: «не только ошибочным, но и невозможным», как выразился Галилей.

Но что «следующее самое простое»? Можно допустить, что скорость падающего тела, начинающего двигаться из положения покоя, пропорциональна протекшему времени. Это — хорошо известный закон, к которому в конечном счете пришел Галилей. В современных обозначениях он выражается уравнением,

и движение, удовлетворяющее этому уравнению, может, конечно, начинаться из положения покоя.

5. Фон[73]. Мы не можем не восхищаться свойственным Галилею мужеством ума, его свободой от философских предрассудков и ми-

212

стицизма. Однако мы должны восхищаться и достижениями Кеплера, а Кеплер, современник Галилея, находился под глубоким влиянием мистицизма и предрассудков своего времени.

Нам трудно ясно понять позицию Кеплера. Современный читатель поражается такому названию как «Введение в космографические исследования, содержащее КОСМИЧЕСКУЮ ТАЙНУ о замечательной пропорции небесных орбит и подлинные и должные причины числа, величины и периодических движений небес, доказанные с помощью пяти правильных тел». Содержание еще более поразительно: астрономия переплетается с теологией, геометрия перемешана с астрологией. Однако каким бы экстравагантным ни казалось кое-что из этого содержания, эта первая работа Кеплера отмечает начало его великих астрономических открытий и, кроме того, живо и привлекательно обрисовывает его личность. Его жажда знаний восхитительна, хотя она почти равняется его жажде таинственного.

Как совершенно правильно говорит название его работы, Кеплер намеревается открыть причину или основание числа планет, их расстояний от Солнца, периодов их вращения. В самом деле, он спрашивает: почему существует ровно шесть планет? Почему их орбиты расположены именно так? Эти вопросы звучат странно для нас, но не звучали так для некоторых из его современников[74]. Однажды он подумал, что нашел секрет, и записал в своей записной книжке: «Земная орбита, или сфера, является мерой всего. Опишите вокруг нее додекаэдр: сфера, окружающая его, есть Марс. Опишите вокруг Марса тетраэдр: сфера, окружающая его, есть Юпитер. Опишите вокруг Юпитера куб: сфера, окружающая его, есть Сатурн. Теперь впишите в Землю икосаэдр: сфера, содержащаяся в нем, есть Венера. Впишите в Венеру октаэдр: сфера, содержащаяся в нем, есть Меркурий. Теперь вы имеете основание для числа планет».

Таким образом Кеплер представляет себе 11 концентрических поверхностей: 6 сфер, перемежающихся с 5 правильными многогранниками. Первая и самая внешняя поверхность — сфера, и каждая поверхность вписана в предыдущую. Каждая сфера связана с планетой: радиус сферы равен расстоянию (среднему расстоянию) планеты от Солнца. Каждый правильный многогранник вписан в предыдущую, окружающую сферу, и описан вокруг следующей, окруженной сферы.

И Кеплер добавляет: «Мне никогда не удастся найти слов, чтобы выразить свое восхищение этим открытием».

Кеплер (в этом отношении современный ученый) тщательно сравнивает свое предположение с фактами. Он составляет таблицу, представленную здесь в слегка модернизированной форме в качестве табл. I (см. стр. 214).

214

Таблица I

Теория Кеплера в сравнении с наблюдениями

Планеты (1)	Наблюдение Коперника (2)	Теория Кеплера (3)	Правильные многогранники (4)
Сатурн	0,635	0,577	Куб
Юпитер	0,333	0,333	Тетраэдр
Марс	0,757	0,795	Додекаэдр
Земля	0,794	0,795	Икосаэдр
Венера	0,723	0,577	Октаэдр
Меркурий

Столбец (1) перечисляет планеты в порядке убывания расстояний от Солнца; он содержит шесть строк, на одну больше, чем следующие столбцы. Столбец (2) содержит отношения расстояний двух соседних планет от Солнца, согласно Копернику; каждое отношение помещено между теми строками, где указаны названия соответствующих планет; расстояние внешней планеты — знаменатель. Столбец (4) перечисляет пять правильных многогранников в порядке, выбранном Кеплером. Столбец (3) указывает отношение радиусов вписанной и описанной сфер для соответствующего правильного многогранника. Числа в одной и той же строке должны находиться в согласии. На самом же деле согласие хорошее в двух случаях и очень плохое в трех остальных.

Теперь Кеплер (что менее славным образом напоминает нам современного ученого) начинает менять точку зрения и модифицировать свое первоначальное предположение. (Основная модификация состоит в том, что он сравнивает расстояние Меркурия от Солнца не с радиусом сферы, вписанной в октаэдр, а с радиусом окружности, вписанной в квадрат, по которому некоторая плоскость симметрии пересекает октаэдр.) Однако он не приходит к какому-нибудь потрясающему согласию между предположением и наблюдением. Все же он остается верен своей идее. Шар — «наиболее совершенное тело», и следующие за ним пять правильных многогранников, известных Платону, являются «благороднейшими телами». У Кеплера мелькает мысль, что бесчисленные мириады неподвижных звезд могут иметь какое-то отношение к неразличимому множеству неправильных тел. И ему кажется «естественным», что Солнце и планеты, самые превосходные творения, как-то связаны с самыми превосходными эвклидовыми телами. Это могло бы оказаться секретом мироздания, «Космической тайной».

С современной точки зрения предположение Кеплера может казаться нелепым. Мы знаем много связей между наблюдаемыми фактами и математическими понятиями, но это связи совсем другого характера.

215

Нам не известна ни одна полезная связь, которая имела бы какую-нибудь ощутимую аналогию с предположением Кеплера. Наиболее странным мы находим то, что Кеплер мог верить в существование чего-то глубоко скрытого за числом планет и задавать такой вопрос: Почему существует ровно шесть планете?

Может возникнуть искушение отнестись к предположению Кеплера как к странному заблуждению. Однако нам следовало бы учитывать возможность, что некоторые теории, которые мы с почтением обсуждаем сегодня, могут рассматриваться как странное заблуждение, если и не будут совершенно забыты, в недалеком будущем. Я думаю, что предположение Кеплера чрезвычайно поучительно. Оно с особой ясностью показывает обстоятельство, которое стоит иметь в виду: доверие, с которым мы относимся к предположению, неизбежно зависит от всего нашего фона, от всей научной атмосферы нашего времени.

6. Неисчерпаем. Предыдущий пример выдвигает на передний план важную особенность правдоподобных рассуждений. Попытаемся описать ее с известной степенью общности.

Мы имеем некоторое предположение, скажем A. Это значит, что A — ясно сформулированное, но не доказанное предложение. Мы подозреваем, что A верно, но в действительности не знаем, верно A или нет. Все же у нас есть некоторая уверенность в своем предположении A. Такая уверенность может иметь, но не обязательно имеет, отчетливое основание. Предположение A совершенно внезапно возникает после продолжительной и явно безуспешной работы над какой-либо задачей. Это предположение A может казаться единственным выходом из запутанной ситуации; оно может казаться почти несомненным, хотя мы и не могли бы сказать почему.

Однако, когда пройдет известное время, нам могут прийти в голову какие-нибудь более отчетливые доводы, которые, хотя и не доказывают A, определенно говорят в его пользу: доводы по аналогии, по индукции, по родственным случаям, по общему опыту или по свойственной самому A простоте. Такие доводы, не давая строгого доказательства, могут сделать A очень правдоподобным.

Но то, что мы поверили в это предположение без каких-либо отчетливо сформулированных аргументов, должно было бы послужить нам предостережением.

И мы последовательно осознаем эти аргументы. Был первый ясный пункт, который нам удалось отделить от темного фона. Однако за этим пунктом в фоне есть еще что-то, так как впоследствии нам удалось выделить другой ясный аргумент. И таким же образом за каждым выясненным пунктом может быть еще что-то. Возможно, этот фон неисчерпаем. Возможно, наша уверенность в предположении никогда не основывается только на выясненных основаниях, такая уверенность может как-то нуждаться во всем нашем фоне как базисе[77].

216

Все же правдоподобные основания важны, и особенно важны выясненные правдоподобные основания. Имея дело с доступной наблюдению действительностью, мы никогда не можем прийти к доказанной истине, мы всегда должны полагаться на какое-то правдоподобное основание. Имея дело с чисто математическими вопросами, мы можем прийти к строгому доказательству. Однако прийти к нему может оказаться очень трудно, и рассмотрение предположительных, правдоподобных оснований может дать нам временную поддержку и может в конечном счете привести нас к открытию окончательного доказательства.

Эвристические доводы важны, хотя они ничего не доказывают. Выяснить наши эвристические доводы также важно, хотя за каждым так выясненным доводом может оказаться еще что-нибудь — возможно какое-нибудь все еще темное, еще более важное основание[75].[78]

Это подсказывает другое замечание: если в каждом конкретном случае мы можем выяснить только некоторые из наших правдоподобных оснований и ни в каком конкретном случае всех их не исчерпываем, то как могли бы мы надеяться исчерпывающим образом абстрактно описать все виды правдоподобных оснований?

7. Обычные эвристические допущения. Два из наших примеров (§§ 2 и 3) поднимают другой вопрос. Напомним кратко одну из ситуаций и коснемся сходной ситуации.

Работая над какой-нибудь задачей, вы получили из явно различных источников столько же уравнений, сколько у вас неизвестных. Вам следует знать, что n уравнений не всегда достаточно для определения n неизвестных: уравнения могут оказаться взаимно зависимыми или противоречивыми. Тем не менее такой случай является исключительным[79], и, таким образом, разумно, пожалуй, надеяться, что ваши уравнения будут определять ваши неизвестные. Поэтому вы идете вперед, преобразуете свои уравнения и смотрите, что из них вытекает. Если имеется противоречие или неопределенность, то это как-то обнаружится. С другой стороны, если вы придете к точному результату, то можете почувствовать бо́льшую склонность потратить время и усилия на строгое доказательство.

Решая другую задачу, вы приходите к почленному интегрированию бесконечного ряда. Вам следует знать, что такая операция не всегда позволительна и может привести к неверному результату. Тем не менее такой случай является исключительным, и, таким образом, разумно, пожалуй, надеяться, что ваш ряд будет вести себя как следует. Поэтому может оказаться целесообразным идти вперед, посмотреть, что вытекает из вашей формулы, не полностью доказанной, и отложить заботы о полном доказательстве[80].

217

Мы коснулись здесь двух обычных эвристических допущений: одного — относительно системы уравнений, другого относительно бесконечного ряда. Такие допущения имеются в каждой области математики, и одним из главных достоинств специалиста в этой области является знание распространенных допущений и знание того, как ими можно воспользоваться и насколько им можно доверять.

Конечно, не следует чрезмерно доверять ни любой догадке, ни обычным эвристическим допущениям, ни вашим собственным предположениям. Без доказательства верить, что ваша догадка справедлива, было бы глупо. Однако предпринять какую-то работу в надежде, что ваша догадка может оказаться справедливой, пожалуй, разумно. Осторожный оптимизм — разумная позиция.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ XI

1. Даны основание треугольника a, высота h, опущенная на a, и угол α, противоположный a. следует: (a) построить треугольник, (b) вычислить его площадь. Все ли данные необходимы?

2. Даны высота трапеции h, средняя линия m, параллельная двум основаниям трапеции и находящаяся от каждой из них на одинаковом расстоянии, в углы α и β между одним из оснований и двумя остальными (наклонными) сторонами. Следует: (a) построить трапецию, (b) вычислить ее площадь. Все ли данные необходимы?

3. Пояс есть часть поверхности шара, содержащаяся между двумя параллельными плоскостями. Высота пояса есть расстояние между этими двумя плоскостями. Даны радиус шара r, высота пояса h и расстояние d от центра шара до той ограничивающей плоскости, которая ближе к центру. Найдите поверхность пояса. Есть какие-нибудь замечания?

4. Первая сфера имеет радиус a. Вторая сфера, радиуса b, пересекает первую сферу и проходит через ее центр. Вычислите площадь той части второй сферы, которая лежит внутри первой. Есть какие-нибудь замечания? Проверьте крайние случаи.

5. Пересмотрим пример § 2 и докажите решение.

6. Шаровой сегмент есть часть шара, содержащаяся между двумя параллельными плоскостями. Его поверхность состоит из трех частей: сферического пояса и двух кругов, называемых основанием и крышкой сегмента. Мы пользуемся следующими обозначениями:

a — радиус основания,

b — радиус крышки,

h — высота (расстояние между основанием и крышкой),

M — площадь среднего поперечного сечения (параллельного основанию и крышке и находящегося от них на одинаковом расстоянии),

V — объем сегмента.

Даны a, b и h; найдите Mh — V.

Есть какие-нибудь замечания? Проверьте несколько крайних случаев.

7. Ось конуса проходит через центр шара. Поверхность конуса пересекает поверхность шара по двум окружностям и делит шар на две части: «конически продырявленный шар» и «пробку» (см. фигуру на рис. 11.2, которую следует вращать вокруг прямой AB); пробка находится внутри конуса. Пусть r обозначает радиус шара, c — длину хорды, образующей при вращении коническое отверстие, и h (высота продырявленного шара) — проекцию c на ось конуса. Даны r, c и h. Найдите объем конически продырявленного шара. Есть какие-нибудь замечания?

218

8. Ось параболоида вращения проходит через центр шара, и их поверхности пересекаются по двум окружностям. Вычислите объем кольцеобразного тела, заключенного между этими двумя поверхностями [внутри шара и вне параболоида), если даны: радиус шара r, проекция h кольцеобразного тела на ось параболоида и расстояние d центра шара от[81] вершины параболоида. [Вращайте рис. 11.3 вокруг OX.) Есть какие-нибудь замечания?

Рис. 11.2. Конически продырявленный шар.	Рис. 11.3. Параболически продырявленный шар.

9. Даны нижнее основание трапеции a, верхнее основание b и высота h; a > b. Трапеция, вращаясь вокруг своего нижнего основания, описывает тело вращения (цилиндр, прикрытый двумя конусами), для которого найдите (a) объем и (b) площадь поверхности. Достаточно ли данных для определения неизвестных?

10. Десять чисел, выбранных в определенном порядке, u₁, u₂, u₃, …, u₁₀,, связаны так, что, начиная с третьего, каждое из них является суммой двух предыдущих:

u_n, = u_n-1 + u_n-2 для u = 3, 4, …, 10.

Дано u₇; найдите сумму всех десяти чисел u₁ + u₂ + … + u₁₀.

11. Вычислите

Есть какие-нибудь замечания? Проверьте случаи α = 0, α → ∞, α → — ∞.

12. Обобщите пример 11. [Сначала попробуйте самое простое.]

13. Напишите одно уравнение с одним неизвестным, не определяющее неизвестного.

14. Если природа неизвестных ограничена подходящим добавочным условием, то одно уравнение может определять несколько неизвестных. Например, если x, y и z, — действительные числа, то они полностью определяются уравнением

x²+ y² + z² = 0.

Найдите все системы положительных целых чисел x, y, удовлетворяющие уравнению x²+ y² = 128.

15. Найдите все системы положительных целых чисел x, y, z, w, удовлетворяющие уравнению x²+ y² + z² + w² = 64.

16. Общий случай. Рассмотрите систему трех линейных уравнений с тремя неизвестными:

a₁x + b₁y + c₁z = d₁,

a₂x + b₂y + c₂z = d₂,

a₃x + b₃y + c₃z = d₃.

219

Предполагаем, что 12 данных чисел a₁, b₁, c₁, d₁, a₂, …, d₃ — действительные числа. Система называется определенной, если существует бесконечное множество решений и несовместной, если решений нет. С разных точек зрения случай, когда система является определенной, выступает как общий, обычный, нормальный, правильный случай, а другие случаи — как исключительные, необычные, ненормальные, неправильные.

(a) Геометрически мы можем интерпретировать множество трех чисел x, y, z как точку в прямоугольной системе координат, а каждое уравнение как множество точек, ему удовлетворяющих как плоскость. (На самом деле для такой интерпретации мы должны допустить, что в левой части каждого уравнения имеется по крайней мере один не равный нулю коэффициент, но будем так и считать.) Система трех уравнений является определенной, если три плоскости имеют только одну общую точку. Когда они имеют две общие точки, они имеют и общую прямую, и, таким образом, система является неопределенной. Когда три плоскости параллельны одной и той же прямой, но не имеют точек, общих всем трем, система несовместна. Если три плоскости находятся в «общем положении», если они «выбраны наугад», то они имеют только одну общую точку, и система является определенной.

(b) Алгебраически система трех уравнений является определенной в том и только в том случае, если определитель из 9 коэффициентов левой части не равен нулю. Следовательно, система является определенной, если на коэффициенты не наложено специальное условие или ограничение в форме уравнения.

(c) Множество из девяти (действительных) коэффициентов (a₁, a₂, a₃, b₁, … c₃) мы можем интерпретировать как точку в девятимерном пространстве. Точки, соответствующие системам, не являющимся определенными (неопределенным или несовместным), удовлетворяют уравнения (определитель = 0), и, значит, они образуют многообразие низшей размерности (восьмимерную «гиперповерхность»),

(d) Бесконечно невероятно, чтобы система трех линейных уравнений с тремя неизвестными, заданная наугад, оказалась неопределенной. Ср. пример 14.23.

17. Рассмотрите для каждого из пяти правильных многогранников вписанную и описанную сферы и вычислите отношения их радиусов.

18. Столбец (3) табл. I остался бы неизменным, если бы мы переменили местами куб и октаэдр или додекаэдр и икосаэдр. Эта неопределенность должна была представлять для теории Кеплера существенное затруднение. Однако Кеплер проявлял необычайную изобретательность в изыскании причин, по которым одно из пяти благородных тел должно обладать более высоким благородством, чем другое, и главенствовать над ним, как барон главенствует над баронетом.

Найдите некоторое простое геометрическое свойство, отличающее три многогранника, которые Кеплер поместил вокруг земной орбиты, от двух, которые он поместил в этой орбите.

19. Никакая идея не является действительно плохой. «Многие догадки оказались ошибочными, но тем не менее полезными, приводя к лучшей догадке». «Никакая идея не является действительно плохой, если мы не принимаем все без критики. Что действительно плохо, это не иметь никакой идеи вообще»[76]. Я почти ежедневно пользуюсь этими сентенциями, чтобы утешить того или иного студента, предлагающего какую-нибудь честную, но наивную идею. Эти сентенции подходят и к тривиальным повседневным ситуциям и к научному исследованию[82]. Наиболее эффектно они подходят к случаю Кеплера.

Самому Кеплеру с его своеобразным переходным от средневековой к современной точке зрения состоянием ума его идея сочетания шести планет с пятью правильными многогранниками казалась ослепительной. Однако я не могу себе представить, чтобы такую идею мог возыметь современник Кеплера Галилей.

220

Современному нам уму эта идея должна с самого начала казаться довольно плохой, потому что она имеет так мало отношения ко всем остальным нашим знаниям о природе. Предположение Кеплера, даже если бы оно и находилось в лучшем согласии с наблюдениями, было бы подкреплено слабо, потому что оно не подкреплялось бы аналогией с чем-либо известным из других источников.

Тем не менее догадка Кеплера, оказавшаяся ошибочной, самым несомненным образом была полезной для перехода к лучшей догадке. Она привела Кеплера к более тщательному исследованию средних расстояний планет, их орбит, их времен обращения, для которых он надеялся найти какое-нибудь подобное же «объяснение», и таким образом она в конце концов привела к знаменитым законам движения планет Кеплера, к Ньютону и ко всем нашим современным научным воззрениям.

20. Несколыко обычных эвристических допущений. Эта тема заслуживала бы более полного разбора, однако мы ограничимся очень коротким перечнем и отрывочными замечаниями. Мы должны быть осторожны, когда интерпретируем слова «вообще говоря» в «практическом», неизбежно несколько туманном, смысле.

«Если в системе уравнений столько же уравнений, сколько и неизвестных, то „вообще говоря“ неизвестные определяются».

Если в задаче столько же условий, сколько имеющихся в распоряжении параметров, то разумно начать с ориентировочного допущения, что задача имеет решение. Например, квадратичная форма от n переменных имеег n(n + 1)/2 коэффициентов, а ортогональное преобразование n переменных зависит от n(n — 1)/2 параметров. Поэтому с самого начала довольно правдоподобно, что подходящим ортогональным преобразованием любая квадратичная форма от n переменных может быть приведена к выражению

y₁, y₂, …, y_n, — новые переменные, введенные преобразованием, а λ₁, λ₂, …, λ_n, — — подходящие параметры. В самом деле, это выражение зависит от n параметров, и

n(n + 1)/2 = n(n — 1)/2 + n.

Это замечание, возникающее после доказательства этого предложения в частных случаях n = 2 и n = 3, и объяснение геометрического смысла этих случаев могут вызвать довольно сильную уверенность в том, что верен и общий случай.

«Две предельные операции вообще говоря коммутативны».

Если одна из этих предельных операций — суммирование бесконечного ряда, а другая — интегрирование, то мы имеем случай, упомянутый в § 7).

«Что верно до предела, то вообще говоря верно и в пределе»[77].

Если дано, что а_n > 0 и то мы не можем заключить, что a > 0; верно лишь, что и a ≥ 0. Рассмотрим кривую как предел вписанных ломаных и поверхность — как предел вписанных многогранников. Вычисление длины кривой как предела длины вписанной ломаной дает правильный результат, однако вычисление площади поверхности как предела площади поверхности вписанного многогранника мажет дать неправильный результат[78]. Высказанный эвристический принцип, хотя он и легко может ввести нас в заблуждение, является наиболее благодарной почвой для появления новых идей. См., например, пример 9.24.

«Неизвестную функцию сначала рассматривайте как монотонную».

221

Мы следовали чему-то похожему на этот совет в § 2, когда допустили, что с изменением формы тела изменяется и его объем, и мы были введены в заблуждение. Тем не менее высказанный принцип часто бывает полезен. Возможно, нам потребуется доказать неравенство вида

где а > b. Мы можем начать, пробуя доказать большее, а именно:

f(x) < g(x).

Это сводится к тому, чтобы сначала допустить, что функция, имеющая производную g(x) — f(x), монотонна. (Задача состоит в сравнении значений этой функции для х = a и х = b.) Высказанный принцип содержится в более общем эвристическом принципе: «сначала попробуйте самое простое».

«Вообще говоря, функция может быть разложена в степенной ряд, первый член которого дает приемлемое приближение, и чем больше членов мы возьмем, тем лучшим будет приближение».

Без должным образом понимаемого ограничения «вообще говоря» это утверждение было бы вопиющим образом неверно. Тем не менее физики, инженеры и другие ученые, применяющие в сваей науке математический анализ, по-видимому, особенно его любят[83]. Оно включает в себя другой принцип, даже более широкий, чем тот, который мы сформулировали ранее: «Неизвестную функцию сначала рассматривайте как линейную». Действительно, если мы имеем разложение

f(x) = а₀ + а₁x + а₂x² + а₃x³ + …,

то мы можем приближенно взять

f(x) ~ а₀ + а₁x.

(Следует замегить, что Галилей, на знавший анализа бесконечно малых, уже отдавал сильное предпочтение линейной функции; см. § 4.) Настоящий принцип лежит в основе той значимости, которую часто приписывают начальному члену относительной погрешности; см. § 5 (2). Этот принцип часто бывал полезен, наталкивая на какую-нибудь идею, близкую к истине, однако он легко может натолкнуть и на что-нибудь очень далекое от истины.

В самом деле, физик (или инженер, или биолог) может прийти к убеждению, что физическая величина y зависит от другой физической величины x так, что имеет место дифференциальное уравнение

Теперь интегрирование, требующееся для решения этого уравнения, может оказаться слишком трудным или вид функции f(y) может быть неизвестен. В обоих случаях физик разлагает функцию f(y) по степеням y, и он может рассматривать как последовательные приближения возникающие при этом дифференциальные уравнения:

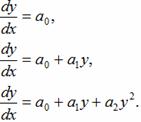
Однако этим трем уравнениям удовлетворяют кривые весьма различной природы и приближение может оказаться только вводящим в заблуждение. К счастью, физики больше полагаются на тщательное рассуждение, чем на

222

аккуратную математику, и, такилг образом, оии с помощью подобных приемов получали хорошие результаты даже в тех случаях, когда математическая ошибка была менее очевидна и потому более опасна, чем в нашем примере.

21. Вознагражденный оптимизм. Даны величины a, b, c, d, e, f, g и h. Исследуем, допускает ли система четырех уравнений с четырьмя неизвестными x, y, u и v:

ax + by + cv + du = 0,

ex + fy + gv + hu = 0,

hx + gy + fv + eu = 0,

dx + cy + bv + au = 0,

решение, отличное от тривиального решения x = y = u = v = 0. Система (S) имеет, как мы знаем, нетривиальное решение в том и только в том случае, если ее определитель равен нулю, но мы хотим избежать непосредственного вычисления этого определителя четвертого порядка. Своеобразная симметрия системы (S) может натолкнуть на мысль положить

y = x, v = y.

Тогда первое уравнение системы (S) совпадает с четвертым, а второе с третьим, так что система четырех уравнений сведется к системе только двух различных уравнений:

(a + d)x+ (b + c)y = 0,

(e + h)x+ (f + g)y = 0.

Эта система допускает нетривиальное решение в том и только в том случае, если ее определитель равен нулю.

Однако мы можем также преобразовать систему (S), полагая

u = – x, v = – y.

Опять мы получаем только два различных уравнения:

(a — d)x+ (b — c)y = 0,

(e — h)x+ (f — g)y = 0.

Обращение в нуль определителя первой или второй системы двух уравнений влечет за собой обращение в нуль определителя системы (S). Поэтому (если мы достаточно оптимистичны) мы можем подозревать, что этот последний определитель четвертого порядка является произведением двух указанных определителей второго порядка.

(a) Докажите это и обобщите результат на определители n-го порядка.

(b) В каком отношении были мы оптимистичны?[84]

22. Возьмите систему координат как в § 9.4. Ось x горизонтальна, а ось y направлена вниз. Соедините начало координат с точкой (a, b)

(1) прямой,

(2) дугой окружности с центром на оси x.

Материальная точка, начинающая двигаться из положения покоя в начале координат, достигает точки (a, b,) за время T₁, или T₂, в зависимости от того, скользит ли она (без трения) вниз по прямой (1) или по дуге (2). Галилей (как рассказано в § 9.4) считал, что T₁ > T₂. После некоторой обработки это неравенство оказывается равносильным следующему:

где мы полагаем

a²(a² + b²)^–1 = h.

Мы могли бы попытаться доказать это неравенство, разложив обе части равенства по степеням h. Что было бы самой простой (или «наиболее оптимистической») возможностью?

223

23. Числовые выкладки и инженер. Неспециалист склонен думать, что числовые выкладки ученого непогрешимы, но скучны. На самом деле числовые выкладки ученого могут быть захватывающе рискованны, но ненадежны. Древние астрономы пытались, а современные инженеры пытаются получить числовые результаты, касающиеся недостаточно известных явлений с помощью недостаточно известных математических средств. Едва ли удивительно, что такие попытки могут не удаваться; куда более удивительно, что часто они удавались. Вот типичный пример. (Технические детали, пропущенные здесь, будут опубликованы где-нибудь в другом месте.)

Инженер хочет вычислить некоторую физическую величину Q, связанную с квадратом со стороной 1. (В действительности Q — жесткость на кручение бруса с квадратным поперечным сечением, но читателю нет необходимости это знать, фактически он не обязан даже знать что такое жесткость на кручение.) Точное решение упирается в математические трудности и поэтому наш инженер, как инженеры часто делают, обращается к приближениям. Следуя определенному методу аппроксимации, он делит данный квадрат на равные «элементы», т. е. на n² меньших квадратов, каждый площади 1/n². (Аппроксимируя двойной интеграл, мы также подобным же образам разбиваем данную площадь на элементы. Важно разумно ожидать, что, когда n стремимся к бесконечности, приближенное значение стремится к истинному значению. На самом же деле, однако, когда n возрастает, трудность вычислений также возрастает и так быстро, что вскоре становится непреодолимой. Инженер рассматривает только случаи n = 2, 3, 4, 5 и получает для Q соответствующие приближенные значения:

0,0937 0,1185 0,1279 0,1324.

Не забудем, что эти числа соответствуют значениям

¹/₄ ¹/₉ ¹/₁₆ ¹/₂₅

площадей маленьких квадратов, использованных при вычислениях.

Инженер изображает эти результаты графически. Он решает наносить приближенные значения, полученные для Я, как ординаты, но колеблется относительво выбора абсциссы. Сначала он пробует в качестве абсциссы n, затем 1/n

Рис. 11.4. Испытание: абсцисса n.	Рис. 11.5. Другое испытание: абсцисса n.	Рис. 11.6. Абсцисса 1/n^2: удача!

и наконец 1/n² (что является численным значением площади маленького квадрата, использованного при аппроксимации); см., соответственно, рис. 11.4, 11.5 и 11.6. Последний выбор является самым лучшим: четыре точки на рис. 11.6 приблизительно лежат на одной прямой. Замечая это, инженер продолжает эту прямую до тех пор, пока она не пересечет вертикальную ось, и рассматривает ординату точки пересечения как «хорошее» приближение для Q.

(a) Почему? На какой идее это основано?

(b) Проверьте рис. 11.6 численно: соедините каждую точку со следующей прямолинейным отрезком и вычислите три угла наклона.

(c) Выберите две наиболее надежные точки на рис. 11.6, воспользуйтесь прямой, проходящей через них в конструкции инженера, вычислите получающееся в результате приближения для Q и сравните его с истинным значением Q, равным 0,1406.

ЗАКЛЮЧИТЕЛЬНОЕ ЗАМЕЧАНИЕ К ПЕРВОМУ ТОМУ

Читатель, внимательно прочитавший предыдущие главы и решивший некоторые из предыдущих задач, имел хороший случай познакомиться с некоторыми сторонами правдоподобных рассуждений. Сформировать общую идею природы правдоподобных рассуждений является целью остающихся пяти глав этого труда, собранных в томе II. Эта цель, я верю, представляет значительный теоретический интерес, но она может иметь и некоторое практическое значение: мы можем лучше выполнить конкретную задачу, если лучше понимаем лежащую в ее основе абстрактную идею.

Главным предметом тома II является формулировка некоторых схем правдоподобных рассуждений. Однако эти схемы будут извлечены из конкретных примеров и изложены в тесной связи с ними. Поэтому том II прибавит к примерам, рассмотренным в томе I, еще несколько математических примеров и будет трактовать их в том же духе.

СХЕМЫ ПРАВДОПОДОБНЫХ УМОЗАКЛЮЧЕНИЙ

Том II

ПРЕДИСЛОВИЕ КО II ТОМУ

Индуктивные рассуждения — одно из многих полей сражения для столкновения философских мнений, и при этом сегодня еще сравнительно полное жизни. Читатель, внимательно прочитавший 1 том этого труда, имел хорошую возможность заметить две вещи. Во-первых, индуктивные рассуждения и рассуждения, основанные на аналогии, играют в математическом открытии главную роль. Во-вторых, и индуктивные рассуждения, и рассуждения, основанные на аналогии, являются частными случаями правдоподобных рассуждений. Мне кажется, с философской точки зрения лучше рассматривать общую идею правдоподобных рассуждений вместо ее изолированных частных случаев. Настоящий том II пытается сформулировать некоторые схемы правдоподобных рассуждений, исследовать их связи с теорией вероятностей и выяснить, в каком смысле они могут рассматриваться как «правила» правдоподобных рассуждений. Будет также кратко обсуждена и их связь с изобретением в математике.

Текст настоящего тома II не часто в явной форме ссылается на том I, и читатель может понять главные связи, не пользуясь этими ссылками. Среди задач, приложенных к различным главам, имеется несколько таких, которые читатель не сумеет решить, не справляясь в томе I, но в целом том II в первом приближении можно читать, не прочитав тома I. Однако, конечно, более естественно прочитать том II после тома I, примеры которого обеспечивают предстоящее нам исследование экспериментальными данными и богатым фоном[79]

Такие данные и фон особенно желательны ввиду метода, которому я буду следовать. Я хочу исследовать правдоподобные рассуждения, поступая как натуралист: я собираю наблюдения, высказываю заключения и подчеркиваю пункты, в которых мои наблюдения кажутся подкрепляющими мои заключения. Однако я уважаю мнение

228

читателя и не хочу силой или обманом побуждать его принять мои заключения

Конечно, представленные взгляды нисколько не претендуют на окончательность. На самом деле имеется несколько мест, где я ясно чувствую необходимость улучшений, меньших или больших. Однако я верю, что главное направление правильно и что обсуждения и, особенно, примеры этого труда могут объяснить «двойственную природу» и «дополнительные стороны» правдоподобных и особенно индуктивных рассуждений, которые иногда кажутся «объективными», а иногда «субъективными».

Дьердь Пойа

Стэнфордский университет,

май 1953 г.

XII. НЕСКОЛЬКО БРОСАЮЩИХСЯ В ГЛАЗА СХЕМ[80][85]

Я не хочу на этой стадии исследовать логическое оправдание этой формы аргументации; пока я рассматриваю ее как практику, которую мы можем наблюдать в поведении людей и животных. — Бертран Рассел[81]

1. Подтверждение следствия. В первом томе этого труда, посвященном Индукции и аналогии в математике, мы нашли некоторую возможность познакомиться с практикой правдоподобных рассуждений. В настоящем втором томе мы собираемся описать эту практику в общем виде. Примеры первой части уже указали некоторые формы схем правдоподобных рассуждений. В настоящей главе мы собираемся сформулировать несколько таких схем в явном виде[82].

Начнем со схемы правдоподобного умозаключения, которая имеет такое общее употребление, что мы могли бы извлечь ее почти из любого примера. Однако мы возьмем пример, который еще не рассматривали раньше.

Эйлеру[83] принадлежит следующее предположение:

Любое целое число вида 8n + 3 является суммой квадрата и удвоенного простого числа. Эйлер не смог доказать это предположение, и трудность доказательства сегодня кажется, пожалуй, еше большей, чем во времена Эйлера. Однако он удостоверился, что это утверждение верно для всех целых чисел вида 8n + 3 до 200; для n = 1, 2, …, 10 см. табл. 1 на стр. 230.

Такая эмпирическая работа может быть легко проведена дальше; для чисел до 1000 не найдено никаких исключений[86]. Доказывает ли это гипотезу Эйлера[84]. Никоим образом; отнюдь не было бы доказательством даже подтверждение для чисел до 1000000. Тем

230

Таблица 1

11 =	1 + 2 × 5
19 =	9 + 2 × 5
27 =	1 + 2 × 13
35 =	1 + 2 × 17 = 9 + 2 × 13 = 25 + 2 × 5
43 =	9 + 2 × 17
51 =	25 + 2 × 13
59 =	1 + 2 × 29 = 25 + 2 ×17 = 49 + 2 × 5
67 =	9 + 2 × 29
75 =	1 + 2 × 37 = 49 + 2 ×13
83 =	1 + 2 × 41 = 9 + 2 × 37 = 25 + 2 × 29 = 49 + 2 × 17

не менее каждое подтверждение делает предположение несколько более правдоподобным, и мы можем видеть в этом общую схему[85].

Пусть A обозначает некоторое ясно сформулированное предположение, к этому моменту ни доказанное, ни опровергнутое. (Например, A может быть предположением Эйлера, что для n = 1, 2, 3, …

8n + 3 = x² + 2p,

где x — целое, а p — простое число.) Пусть B обозначает некоторое следствие A; B также предполагается ясно сформулированным и к данному моменту ни доказанным, ни опровергнутым. (Например, B может быть первым частным случаем предположения Эйлера, не записанным е табл. I, утверждаюшим, что 91 = x² + 2p.) К настояшему моменту мы не знаем, истинны ли A или B. Мы знаем, однако, что

из A следует B.

Теперь мы предпринимаем проверку B. Чтобы выяснить, будет ли утверждение относительно числа 91 истинно или нет, достаточно нескольких проб. Если бы оказалось, что B ложно, мы могли бы ззключить, что и A ложно. Это совершенно ясно. Мы имеем здесь классическую элементарную схему рассуждения, «modus tollens», так называемого гипотетического силлогизма:

Из A следует B

B ложно

A ложно

Горизонтальная линия, отделяющая две посылки от заключения, заменяет, как обычно, слово «следовательно». Мы имеем здесь доказательное умозаключение хорошо известного типа.

231

Что случится, если B окажется верным? (На самом деле 91 = 9 + 2 × 41 =81 + 2 × 5.) Нет никакого доказательного заключения: подтверждение следствия B предположения A не доказывает A. Однако такое подтверждение делает A более правдоподобным. (Предположение Эйлера, подтвердившееся еше в одном случае, становится несколько более правдоподобным.) Мы имеем схему правдоподобного умозаключения:

Из A следует B

B истинно

A более правдоподобно

Горизонтальная линия снова заменяет слово «следовательно». Мы будем называть эту схему фундаментальной индуктивной схемой или, несколько короче, «индуктивной схемой».

Эта индуктивная схема не говорит ничего удивительного. Напротив, она выражает убеждение, в котором, по-видимому, не сомневается ни один разумный человек: Подтверждение следствия делает предположение более правдоподобным. При небольшой внимательности мы можем в повседневной жизни, в суде, в науке и т. д наблюдать бесчисленное множество рассуждений, соответствующих нашей схеме[87].

2. Последовательное подтверждение нескольких следствий. В этом параграфе словами «разбор теоремы» я пользуюсь в специальном значении «обсуждение, или обзор нескольких частных случаев и нескольких наиболее непосредственных следствий теоремы». Я думаю, что разбор изложенных теорем полезен и в повышенных, и в элементарных классах. Рассмотрим совсем простой пример. Допустим, что вы преподаете в классе стереометрию и должны вывести формулу для площади боковой поверхности усеченного конуса. Конечно, это прямой круговой конус, и вам даны радиус нижнего основания R, радиус верхнего основания r и высота h. Вы проделываете обычный вывод и приходите к результату:

A. Площадь боковой поверхности усеченного конуса равна

Для последующих ссылок обозначим эту теорему буквой A.

Теперь начинается разбор теоремы A. Вы задаете классу вопрос: Можете ли вы проверить результат? Если ответа нет, то вы ставите более прозрачные наводящие вопросы: Можете ли вы проверить его, применяя к какому-нибудь уже вам известному частному случаю? В конечном счете, при большем или меньшем сотрудничестве с частью класса, вы спускаетесь к различным частным

232

случаям. Если R = r, вы получаете первый, заслуживающий внимания частный случай:

B₁. Площадь боковой поверхности цилиндра равна 2πrh.

Конечно, h обозначает высоту цилиндра, а r — радиус основания. Это следствие теоремы A для последующих ссылок мы обозначаем буквой B₁ Следствие B₁ уже изучалось в вашем классе, и, таким образом, оно служит подтверждением для A.

Полагая г=О, вы получаете другой частный случай теоремы A:

Здесь h обозначает высоту конуса, а R — радиус его основания. И это следствие B₂ теоремы A было известно ранее и служит дальнейшим подтверждением A.

Существует менее очевидный, но интересный частный случай, соответствующий h = 0:

B₃. Площадь кольца между двумя концентрическими окружностями с радиусами R и r равна πR² — πr².

Это следствие B₃ теоремы A известно из планиметрии и дает новое подтверждение A.

Три отмеченных частных случая — все они известны по предыдущему изучению — подкрепляют A с трех разных сторон; три тела (цилиндр, конус и кольцо, соответственно отвечающие случаям r = R, r = 0 и h = 0) выглядят совершенно по-разному. Вы можете упомянуть и совсем уж частный случай r = h = 0.

B₄. Площадь круга радиуса R равна πR².

Я иногда замечал, что мальчик в последнем ряду, который до конца моего строгого вывода формулы казался крепко спящим, открывал глаза и обнаруживал некоторый интерес к ходу разбора. Вывод формулы, стандартный и легкий, казался ему непонятным и трудным. Вывод его не убедил. Его больше убеждает разбор: формула, подтверждающаяся в таком большом числе и таких различных случаев, думает он, имеет хорошие шансы оказаться правильной. И думая так, он поступает в соответствии со схемой правдоподобного рассуждения, тесно связанной с фундаментальной индуктивной схемой, но более усложненной, чем эта схема:

Из A следует B_{n + 1}

B_{n + 1} сильно отличается от ранее подтвержденных следствий B₁ B₂, ..., B_n теоремы A

B _{n + 1} истинно

A значительно более правдоподобно

Эта схема уточняет фундаментальную индуктивную схему. Конечно, подтверждение любого следствия усиливает нашу веру в предположение. Однако подтверждение одних следствий усиливает нашу веру

233

больше, а подтверждение других усиливает ее меньше. Только что приведенная схема обращает наше внимание на обстоятельство, имеющее большое влияние на силу индуктивных доводов: разнообразие проверенных следствий. Подтверждение нового следствия имеет большее значение, если новое следствие больше отличается от ранее подтвержденных следствий.

Теперь посмотрил на оборотную сторону медали. Возьмем пример предыдущего § 1. Следующие друг за другом в табл. 1 случаи, в которых подтверждается предположение Эйлера, выглядят очень похожими один на другой, — если мы не подметили никакого скрытого ключа, а кажется очень трудным подметить такой ключ. Поэтому раньше или позже мы устанем от этой однообразной последовательности подтверждений. Проверив какое-то число случаев, мы начинаем колебаться. Стоит ли терять время и браться за следующий случай? Следующий случай, если бы результат его был отрицателен, мог бы опровергнуть предположение, но следующий случай во всех известных нам отношениях так похож на уже проверенные случаи, что мы едва ли можем ожидать отрицательный результат. Следующий случай, если бы результат его был положителен, увеличил бы нашу уверенность в справедливости гипотезы Эйлера, но это увеличение уверенности было бы настолько мало, что оно едва ли стоит усилий, требующихся для испытания этого следующего случая.

Это рассмотрение подсказывает следующую схему, несущественно отличающуюся от только что высказанной схемы и, скорее, являющуюся ее дополнительной формой:

Из A следует B_{n + 1}

B_{n + 1} очень похоже на ранее подтвержденные следствия B₁ B₂, ..., B_n теоремы A

B _{n + 1} истинно

A немножко более правдоподобно

Подтверждение нового следствия имеет большее или меньшее значение в зависимости от того, больше или меньше это новое следствие отличается от ранее неподтвержденных следствий.

3. Подтверждение невероятного следствия. В одной малоизвестной короткой заметке[86] Эйлер рассматривает для положительных значений параметра n ряд

∑α =πГ + 2πГ₄ + 3πГ₅ + … (1)

234

сходящийся для всех значений x. Он прослеживает сумму ряда и ее нули для n = 1, 2, 3, 4.

n = 1:	сумма cos x,	нули ± π/2, ± 3π/2, ± 5π/2, …
n = 2:	сумма (sin x)/x,	нули ± π, ± 2π, ± 3π,
n = 3:	сумма 2(1 — cos x)/x^2,	нули ± 2π, ± 4π, ± 6π,
n = 4:	сумма 6(x — sin x)/ x^3,	нет действительных нулей.

Эйлер наблюдает различие: в первых трех случаях все нули действительные, в последнем случае ни один из нулей не является действительным. Эйлер отмечает более тонкое различие между первыми двумя случаями и третьим случаем: для n = 1 и n = 2 расстояние между двумя соседними нулями равно π (если только в случае n = 2 мы не учитываем расстояние между нулями, ближайшими к началу координат), но для n = 3 расстояние между соседними нулями равно 2π (с аналогичной оговоркой). Это приводит его к поразительному наблюдению: в случае n = 3 все нули являются двойными нулями. «Однако мы знаем из анализа, — говорит Эйлер, — что два корня уравнении при переходе от действительных к мнимым корням всегда совпадают. Таким образом, мы можем понять, почему все нули внезапно становятся мнимыми, когда мы берем для и значение, превосходящее 3». На основании этих наблюдений он высказывает неожиданное предположение: функция, определенная рядом (1), при 0 < n ≤ 3 имеет только действительные нули и бесконечное их множество, но при n > 3 не имеет ни одного действительного нуля. В этом утверждении n он рассматривает как непрерывно меняющийся параметр.

Во времена Эйлера вопросы о действительности корней трансцендентных уравнений были совершенно новыми, и мы должны признаться, что даже сегодня мы не владеем никаким систематическим методом для решения таких вопросов. (Например, мы не можем доказать или опровергнуть известную гипотезу Римана.) Поэтому предположение Эйлера кажется чрезвычайно смелым. Я думаю, что мужество и ясность, с которыми он высказал свое предположение, вызываюг восхишение.

Однако вызывающее восхищение достижение Эйлера в известной степени можно понять. Другие специалисты совершают подобные же подвиги, занимаясь другими вопросами, и каждый из нас нечто подобное совершает в повседневной жизни. Фактически Эйлер догадался о целом по нескольким разрозненным деталям. В точности таким же образом археолог с разумной уверенностью может восстановить всю надпись по нескольким разрозненным буквам на стертом камне. Палеонтолог может надежно описать все животное, исследован несколько его окаменевших костей. Когда человек, которого вы очень хорошо знаете, начинает говорить определенным образом, вы после нескольких слов можете предсказать всю историю, которую он собирается вам поведать. Совершенно подобным же образом

235

Эйлер отгадал всю историю, математическую ситуацию по нескольким ясно осознанным фактам.

Замечательно еще то, что он отгадал ее по такому малому числу фактов, рассматривая только четыре случая n = 1, 2, 3, 4. Нам не следует, однако, забывать, что косвенные улики могут быть очень сильными. Подсудимый обвиняется в том, что он взорвал яхту отца своей приятельницы, и обвинение предъявляет расписку, подписанную подсудимым, удостоверяющую покупку такого-то количества динамита. Такая улика чрезвычайно усиливает доводы обвинения. Почему? Потому, что покупка динамита обыкновенным гражданином сама по себе является очень необычным происшествием, но такую покупку вполне можно понять, если покупатель собирается что-либо или кого-либо взорвать. Пожалуйста, заметьте, что этот судебный случай очень похож на случай n = 3 ряда Эйлера. То, что все корни написанного наугад уравнения оказываются двойными корнями, само по себе является необычным происшествием. Однако вполне можно понять, что при переходе от двух действительных корней к двум мнимым корням появляется двойной корень. Случай n = 3 является наиболее сильной частью косвенных улик, предъявленных Эйлером, и мы можем уловить в этом общую схему[88] правдоподобного умозаключения:

Из A следует B

B само по себе очень невероятно[89]

B истинно

A гораздо[90] более правдоподобно

И эта схема кажется уточнением или усложнением фундаментальной индуктивной схемы (1). Прибавим без специальной иллюстрации дополнительную схему, объясняющую ту же идею с противоположной стороны:

Из A следует B

B само по себе вполне вероятно

B истинно

A немножко более правдоподобно

Подтверждение следствия имеет большее или меньшее значение в зависимости от того, более или менее само по себе вероятно это следствие. Подтверждение наиболее неожиданного следствия является наиболее убедительным.

Между прочим, Эйлер оказался прав: спустя 150 лет его предположение было полностью доказано[87].

236

4. Умозаключение по аналогии. На этом этапе может оказаться поучительным вернуться к примерам из первого тома об Индукции и Аналоги. В предыдущих параграфах этой главы мы сформулировали несколько схем правдоподобных умозаключений: как выглядят упомянутые примеры в свете этих схем?

Рассмотрим вновь два родственных примера (соответственно из §§ 10.1 и 10.4 тома I). Один из этих примеров связан с изопериметрической теоремой и Декартом, другой с физическим аналогом изопериметрической теоремы и лордом Рэлеем. Воспроизведем две таблицы из гл. Х (названные там табл. I и табл. II, а здесь соответственно табл. II и табл. III), поместив их рядом. Табл. II (как она занумерована в этой главе) перечисляет периметры десяти фигур, каждая из которых имеет одну и ту же площадь 1, а табл. III перечисляет основные частоты тех же десяти фигур (рассматриваемых как колеблющиеся мембраны).

Таблица II

Таблица III

Периметры фигур равной площади

Основные частоты мембран равной площади

Круг	3,55
Квадрат	4,00
Квадрант	4,03
Прямоугольник 3 : 2	4,08
Полукруг	4,10
Секстант	4,21
Прямоугольник 2 : 1	4,24
Равносторонний треугольник	4,56
Прямоугольник 3 : 1	4,64
Равнобедренный прямоугольный треугольник	4,84

Круг	4,261
Квадрат	4,443
Квадрант	4,551
Секстант	4,616
Прямоугольник 3 : 2	4,624
Равносторонний треугольник	4,774
Полукруг	4,803
Прямоугольник 2 : 1	4,967
Равнобедренный прямоугольный треугольник	4,967
Прямоугольник 3 : 1	5,736

Периметры в одной таблице, главные частоты в другой расположены в порядке возрастания. Обе таблицы начинаются с круга, имеющего среди перечисленных десяти фигур наименьший периметр, а также наиболее низкую основную частоту, и это наталкивает на две теоремы:

Из всех плоских фигур с данной площадью наименьший периметр имеет круг.

Из всех мембран с данной площадью наиболее низкую основную частоту имеет круг.

Первое утверждение есть изопериметрическая теорема, второе — знаменитая гипотеза лорда Рэлея. Наши таблицы дают серьезные индуктивные доводы в пользу обоих утверждений, но, конечно, не доказывают их.

237

С тех пор как мы рассматривали эти таблицы в §§ 10.1 и 10.4, положение изменилось. За это время мы познакомились с доказательством изопериметрической теоремы (§§ 10.6—10.8, примеры 10.1—10.15). Геометрическое минимальное свойство круга, индуктивно подкрепленное табл. II, было доказано. Естественно ожидать, что аналогичное физическое минимальное свойство круга, индуктивно подкрепленное табл. II), также окажется верным. Ожидая это, мы следуем важной схеме правдоподобного умозаключения:

A аналогично B

B истинно

A более правдоподобно

Предположение становится более правдоподобным, когда оказывается истинным аналогичное предположение.

Применение этой схемы к рассмотренной ситуации кажется разумным. Однако в этой ситуации сушествуют и другие многообешаюшие указания.

5. Углубление аналогии. Таблицы II и III, помещенные рядом, по-видимому, наводят на дальнейшие размышления. Десять рассматриваемых фигур не стоят в обеих таблицах точно в одной и той же последовательности. В этой последовательности есть что-то своеобразное. Расположение фигур в табл. II кажется не слишком отличным от расположения в табл. III, но не это главное. Таблицы содержат различные виды фигур: прямоугольники, треугольники, секторы. В каком же порядке расположены фигуры одного и того же вида? Как выглядела бы более короткая таблица, в которой были бы выписаны только фигуры одного вида? Таблицы содержат несколько правильных фигур: равносторонний треугольник, квадрат и, не забудем, круг. В каком порядке расположены правильные фигуры? Не могли бы мы как-нибудь сравнить фигуры различных видов, например треугольники и секторы? Не могли ли бы мы расширить индуктивную базу, добавив к нашим таблицам новые фигуры? (И этом мы сильно ограничены. Не трудно вычислять площади и периметры, но трудно иметь дело с основными частотами, и их явное выражение известно лишь в очень немногих случаях.) В конечном счете мы получаем табл. IV (см. стр. 238).

Таблица IV выявляет между нашими двумя величинами, зависящими от формы переменной плоской фигуры — периметром и основной частотой, — замечательный параллелизм. (Не следует забывать, что площадь переменной фигуры постоянна, равна 1.) Если мы знаем периметр, то мы никоим образом не в состоянии вычислить основную частоту, и наоборот. Однако, судя по табл. IV, мы должны были бы подумать, что во многих простых случаях эти величины меняются в одном и том же направлении.

238

Таблица IV

Периметры и основные частоты фигур равной плошади

Прямоугольники
1:1 (квадрат)................	4,00	4,443
3:2........................	4,08	4,624
2:1........................	4,24	4,967
3:1........................	4,64	5,736
Треугольники
60° 60° 60°.................	4,56	4,774
45° 45° 60°.................	4,84	4,967
30° 60° 90°.................	5,08	5,157
Секторы
180° (полукруг).............	4,10	4,967
90° (квадрант)..............	4,03	4,967
60° (секстант)..............	4,21	4,967
45°........................	4,44	4,967
36°........................	4,68	4,967
30°........................	4,93	4,967
Правильные фигуры:
круг.......................	3,55	4,967
квадрат....................	4,00	4,967
равносторонний треугольник.	4,56	4,967
Треугольники в сравнении с секторами:
тр. 60° 60° 60°..............	4,56	4,967
сектор 60°.................	4,21	4,967
тр. 45° 45° 60°..............	4,84	4,967
сектор 45°.................	4,44	4,967
тр. 30° 60° 90°..............	5,08	4,967
сектор 30°.................	4,93	4,967

Рассмотрим два столбца числовых данных в этой таблице и перейдем от какой-нибудь строки к следуюшей: если возрастание имеется в одном из столбцов, то соответствующее возрастание имеется и в другом, и если в одном из столбцов имеется убывание, то соответствующее убывание имеется и в другом.

Сосредоточим свое внимание на прямоугольниках. Если отношение длины к ширине возрастает от 1 до ∞, так что форма изменяется от квадрата до бесконечно растянутого прямоугольника, то и периметр и основная частота, по-видимому, монотонно возрастают. Квадрат, который как правильная фигура среди всех четырехугольников является «ближайшим» к кругу, имеет наименьший периметр, а также наименьшую основную частоту. Из трех входящих в таблицу треугольников равносторонний треугольник, который как правильная фигура среди всех треугольников является «ближайшим» к кругу, имеет наименьший периметр, а также наименьшую основную частоту.

Поведение секторов сложнее. Когда угол сектора меняется от 180°

239

до 0°, периметр сначала убывает, достигает минимума, а затем возрастает; и таким же образом изменяется и основная частота. Посмотрим теперь на правильные фигуры. Равносторонний треугольник имеет 3 оси симметрии, квадрат имеет 4 таких оси[91], а круг — бесконечное множество. Насколько мы можем судить по табл. IV, и периметр, и основная частота, по-видимому, убывают, когда возрастает число осей симметрии. В последнем отделе табл. IV каждый треугольник мы сопоставляем с сектором, угол которого равен наименьшему углу треугольника. Во всех трех случаях сектор оказывается «более круглым», имеет наименьший периметр и более низкую основную частоту.

То, что мы определенно знаем относительно этих закономерностей, не выходит за пределы табл. IV. Таблица IV внушает и делает правдоподобным, что эти закономерности сохраняются и за пределами собранного экспериментального материала, но она этого никоим образом не доказывает. Итак, табл. IV приводит нас к нескольким новым предположениям, которые, хотя и похожи на предположение Рэлея, имеют, конечно, значительно более ограниченную сферу действия.

Какое влияние оказывает табл. IV на нашу веру в предположение Рэлея? Можем ли мы в табл. IV найти для него какое-нибудь разумное основание, которого мы не замечали раньше, рассматривая табл. II и III?

Конечно, можем. Прежде всего табл. IV содержит еще несколько частных случаев, в которых подтверждается предположение Рэлея (треугольник 30°, 60°, 90°, секторы с углами 46°, 36° и 30°). Однако здесь есть нечто большее. Аналогия между изопериметрической теоремой и предположением Рэлея стала значительно более глубокой; факты, перечисленные в табл. IV, прибавляют к этой аналогии несколько новых сторон. И вот кажется разумным рассматривать заключение по аналогии как ставшее более сильным, если стала сильнее сама аналогия, на которой основано это заключение. Таким образом, табл. IV значительно усилила позицию Рэлея.

6. Затушеванное умозаключение по аналогии. Однако есть еще кое-что. Как мы заметили, табл. IV подсказывает несколько предположений, аналогичных предположению Рэлея (но имеющих более ограниченную сферу действия). Таблица IV подсказывает эти предположения и вдобавок придает им некоторое правдоподобие. Это же обстоятельство, естественно, несколько увеличивает правдоподобие первоначального предположения Рэлея. Если вы думаете таким же образом, то вы думаете согласно следующей схеме:

A аналогично B

B более правдоподобно

A несколько более правдоподобно

240

Предположение становится несколько более правдоподобным когда становится более правдоподобным аналогичное предположение. Это — ослабленная, или затушеванная форма схемы, сформулированной в § 4.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ XII

1. Таблица I, приводящая некоторые индуктивные доводы в пользу упомянутого в § 1 предположения Эйлера, очень похожа на таблицу в § 1.3, или на табл. I, II и III в гл. IV, или на таблицу Эйлера, приведенную в подкрепление его «Наиболее Необычайного Закона Чисел, Относящегося к Суммам их Делителей», см. 4 6.2. Эти таблицы имеют также сходство с двумя таблицами, приведенными в гл. III, одна в § 3.1 (многогранники), другая в § 3.12 (разбиения пространства). С какой из этих двух таблиц больше сходства?

2. Эйлер, проверив свой «Наиболее Необычайный Закон» [см. § 6.2] для n = 1, 2, 3, 4, …, 20, переходит к подтверждению его для n = 101 и n = 301. Он имеет достаточное основание предпочесть исследование 101 и 301 исследованию 21 и 22 (которое ов ясно высказывает в начале п. 7 своей статьи). Не учитывая или только смутно припоминая содержание Закона Эйлера, не думали ли бы вы, что подтверждение двух его случаев (101 и 301) имеет с точки зрения испытания бо́льшую ценность, чем имело бы подтверждение двух следующих случаев (21 и 2!)7

3. Пусть a, b и c обозначают стороны треугольника, 2p = a + b + c — его периметр, A — площадь.

Проверьте формулу Герона

A² = p(p — a) (p — b)(p — c)

столькими способами, сколькими сумеете.

4. Рассмотрим четырехугольник, вписанный в круг. Пусть a, b, c и d обозначают стороны, 2p = a + b + c + d — его периметр, A — площадь.

Утверждается, что

A² = (p — a)(p — b)(p — c)(p — d)

Проверьте это утверждение столькими способами, сколькими сумеете. Есть ли у вас какие-нибудь замечания?

5. Пусть V обозначает объем тетраэдра, а

a, b, c,

e, f, g

— длины его шести ребер; ребра a, b и c оканчиваются в одной и той же вершине тетраэдра, e — ребро, противоположное ребру a, f — ребру b и g — ребру c. [Два ребра тетраэдра называются противоположными, если они не имеют общей вершины.) Ребра e, f и g являются тремя сторонами грани тетраэдра, противоположной вершине, в которой оканчиваются a, b и c. Утверждается, что

144V² = 4a²b²c² + (b² + c² — e²)(c² + a² — f²)(a² + b² — g²) —

— a²(b² + c² — e²)² — b²(c² + a² — f²)² — c²(a² + b² — g²).

Проверьте это утверждение столькими способами, сколькими сумеете. [Симметрично ли предлагаемое для V выражение относительно шести ребер»]

6. Положим

aⁿ + bⁿ + cⁿ = s_n

для n = 1, 2, 3, … и определим p, q и r с помощью тождества относительно x:

(x — a)(x — b)(x — c) = x³ — px²+ qx — r,

241

так что

p = a + b + c,

q = ab + ac + bc,

r = abc.

(В обычной терминологии p, q и r — «элементарные симметрические функции от a, b и c, а s_n — «сумма одинаковых степеней».) Очевидно, p = s₁. Утверждается, что для произвольных значений a, b и c

если только знаменатель не равен нулю. Проверьте эти формулы в частном случае a = 1, b = 2, c = 3 и еще в трех случаях, указанных в таблице:

Случай	a	b	c
(1)	1	2	3
(2)	1	2	— 3
(3)	1	2	0
(4)	1	2	— 2

Придумайте дальнейшие проверки. В частности, попытайтесь обобщить случаи (2), (3) и (4).

7. Пусть A, B₁, B₂, B₃ и B₄ имеют значение, приданное им в § 2. Дает ли подтверждение B₄, произведенное после подтверждения B₁, B₂ и B₃ добавочные индуктивные доводы в пользу A?

8. Вспомним «Наиболее Необычайный Закон» Эйлера и значение сокращений T, C₁, C₂, C₃, …, C^*₁, C^*₂, C^*₃, …, объясненное в § 6.3. Эйлер индуктивно подкрепил теорему T, когда а~ все еще не был в состоянии ее доказать, подтвердив ее следствия C₁, C₂, C₃, …, C₂₀. (Он, возможно, шел даже дальше.) Затем он открыл, что и C^*₁, C^*₂, C^*₃, … являются следствиями теоремы T, и подтвердил C^*₁, C^*₂, …, и C^*₂₀, C^*₁₀₁, C^*₃₀₁. Благодаря этим новым подтверждениям уверенность Эйлера, по-видимому, значительно усилилась; но можно ли оправдать это усиление? [Здесь нужно обратить более серьезное, чем в примере 2, внимание на детали.]

9. Возвратимся к предположению Эйлера, рассмотренному в § 1; для краткости назовем его «предположением Э». Запишем кратко значение этого сокращения:

Э: 8n + 3 = x² +2p.

Идеи, которая привела Эйлера к его предположению Э, заслуживает упоминания. Эйлер посвятил много труда тем знаменитым предположениям теории чисел, которые Ферма высказал без доказательства. Одно из них (мы называем его «предположением Ф») говорит, что любое целое число является суммой трех треугольных чисел. Запишем кратко значение этого сокращения:

Эйлер подметил, что если бы его предположение Э было верно, то из него легко вытекало бы предположение Ферма Ф. Иными словами, Эйлер убедился, что из Э следует Ф. (Детали см. в следующем примере 10.) Будучи полон решимости доказать предположение Ферма Ф, Эйлер, естественно, желал, чтобы его предположение Э оказалось верным. Было ли это только желанием? Я так не думаю; рассмотренные связи дают какое-то слабое, но не неразумное основание для

242

веры в предположение Эйлера Э в соответствии со следующей схемой:

Из Э следует Ф

Ф правдоподобно

Э несколько правдоподобно[92]

Вот еще одна схема правдоподобного умозаключения. Читателю следовало бы сравнить ее с фундаментальной индуктивной схемой.

10. Доказывая, что из Э следует Ф (в обозначениях предыдущего примера 9), Эйлер пользовался более глубоким результатом, который он доказал предварительно: простое число вида 4n + 1 является суммой двух квадратов. (Оно было индуктивно рассмотрено в примере 4.4.) Принимая его на веру, докажите, что в самом деле из Э следует Ф.

11. После того как у Эйлера возникло его предположение, изложенное в § 3, он испытал его, вычисляя первые нули своего ряда для нескольких значений n. (Под «первым нулем» мы понимаем «нуль», абсолютная величина которого наименьшая. Если x есть первый нуль рассматриваемого ряда, то и – x есть нуль; и x, и – x являются «первыми нулями». Поэтому x будет действительным в том и только в том случае, когда x² положительно.) Конечно, Эйлер должен был вычислять эти нули приближенно. Метод (метод Даниила Бернулли), которым он часто пользовался для подобной цели, дал такие последовательности приближенных значений для первого нуля x в случаях n = ½, ⅓, ¼:

n = ½	n = ⅓	n = ¼
4x^2 ~ 3,000	9x^2 ~ 4,000	16x^2 ~ 4,000
3,281	4,2424	5,2232
3,291	4,2528	5,2302
3,304	4,2532	52304

Во всех трех случаях приближенные значения кажутся стремящимися к положительному пределу монотонно и довольно быстро. Эйлер принял это за признак того, что первые нули действительны, и увидел в этом подтверждение своего предположения.

Постараемся выяснить общую схему эвристического умозаключения Эйлера. Пусть A обозначает его предположение, объясненное в § 3, относительно действительности нулей его ряда. Пусть B обозначает тат факт, что для n = ½ первый нуль действителен. Очевидно, из A следует B. Так вот, Эйлер не доказал B, он только сделал B более правдоподобным. Таким образом, мы имеем здесь следующую схему правдоподобного умозаключения:

Из A следует B

B более правдоподобно

A несколько более правдоподобно

Вторая посылка слабее, чем вторая посылка фундаментальной индуктивной схемы. Слово «несколько» поставлено, чтобы подчеркнуть, что и заключение слабее, чем в фундаментальной индуктивной схеме.

12. Современный математик может вывести из числовых данных предыдущего примера 11 эвристическое заключение более строгое, чем вывел сам Эйлер. Можно показать, что если ряд Эйлера имеет только действительные корни, то последовательные приближенные значения, полученные по методу Даниила Бернулли, непременно образуют возрастающую последовательность[88]. Пусть A обозначает то же предположение, что и в предыдущем примере 11, но B пусть теперь означает другое утверждение, а именно следующее: «Для n = ½ первые четыре приближения, полученные по методу Даниила Бернулли, образуют возрастающую последовательность, и это же имеет место для n = ⅓ и n = ¼».

243

Тогда известно, что имеют место обе посылки фундаментальной индуктивной схемы:

Из B следует B

B истинно

и получающееся в результате эвристическое заключение сильнее.

К предыдущему можно прибавить два замечания:

(1) Эйлер не формулировал только что указанного свойства метода Даниила Бернулли и, конечно, не доказал его. Однако очень вероятно, что, обладая громадным опытом работы по этому методу, он имел какого-то рода индуктивное знание. Так, Эйлер, хотя он и не вывел заключения современного математика, обладал им в менее ясной форме. И, по-видимому, он имел в своем богатом математическом фоне[89] и другие указания, которые он не мог бы полностью сформулировать и которые мы не могли бы обьяснить и сегодня.

(2) Числовые данные, указанные в примере 11, привели автора к подозрению об общей теореме, доказанной в статье, цитированной на предыдущей странице Это — маленький, но конкретный пример пользы индуктивного метода в математическом исследовании.

13. В гл IV мы индуктивно исследовали сумму четырех нечетных квадратов; см. §§ 4.3.—4.6, табл. I. Позднее мы брались за аналогичные задачи, касающиеся четырех произвольных квадратов и восьми квадратов; см примеры 4.10— .23 и табл. II и III. Первое исследование, несомненно, помогло нам распознать закон в последующих случаях. Должна ли также усилиться наша вера в результат последнего исследования из-за результата первого?

14. Индуктивное умозаключение по бесплодным усилиям. Построить с помощью циркуля и линейки сторону квадрата, равную площади круга данного радиуса. Это — строгая формулировка известной задачи о квадратуре круга, придуманной греками. Она не была забыта в средние века, хотя мы не можем верить, что многие понимали тогда ее строгую формулировку; Данте ссылается на нее в теологической кульминации Божественной Комедии, в конце заключительной песни. Этой задаче было около двух тысяч лет, когда французская академия приняла решение, что рукописи, имеющие целью найти квадратуру круга, не будут проверяться. Не проявила ли Академия узость взглядов? Я так не думаю; после бесплодных усилий тысяч людей на протяжении тысячелетий были некоторые основания подозревать, что задача неразрешима.

Вас тянет бросить задачу, не поддающуюся вашим неоднократным усилиям. Если вы упорны или глубоко заинтересованы задачей, то вы прекратите работу только после многих и больших усилий. Если вы не любите больших усилий или не серьезно заинтересованы, то вы прекратите работу после нескольких поверхностных попыток. Но в любом случае имеется своего рода индуктивное умозаключение. Вот рассматриваемое предположение:

A. Справиться с этой задачей невозможно.

Вы наблюдаете:

B. Даже Я не могу справиться с этой задачей.

Это, само по себе, в самом деле очень[93] невероятно. Однако, несомненно,

из A следует B,

и, таким образом, ваше наблюдение относительно B по фундаментальной индуктивной схеме делает A более правдоподобным.

Невозможность квадратуры круга, строго сформулированная, была доказана в 1882 г. Линдеманом, после основной работы Эрмита[94]. Существуют другие сходные задачи, ведущие начало от греков (трисекция угла и удвоение куба), неразрешимость которых, после накопленной очевидности бесплодных усилий, была в конце концов доказана. После бесплодных усилий построить «perpetuum mobile» физики сформулировали «принцип невозможности вечного движения», и этот принцип оказался замечательно плодотворным.

XIII. ДАЛЬНЕЙШИЕ СХЕМЫ И ПЕРВЫЕ СВЯЗИ МЕЖДУ СХЕМАМИ

После того как мы усвоим несколько простых положений …, полезно обозреть их путем последовательного и непрерывного движения мысли, обдумать их взаимоотношения и отчетливо представить одновременно наибольшее их количество; благодаря этому наше знание сделается более достоверным и наш ум приобретет больший кругозор. — Декарт[90]

1. Исследование следствия. Рассмотрим ситуацию, часто встречающуюся в математических изысканиях. Мы хотим решить, истинно ли ясно сформулированное математическое положение A или нет. У нас есть, возможно, какая-то интуитивная уверенность в истинности A, но этого недостаточно: мы хотим доказать A или опровергнуть. Мы работаем над этой задачей, но без решающего успеха. После того как прошло некоторое время, мы замечаем следствие B предложения A. Это B является ясно сформулированным математическим предположением, о котором мы внаем, что оно вытекает из A.

Из A следует B.

Однако мы не знаем, истинно B или нет. При этом нам кажется, что B доступней, чем A; по той или иной причине у нас есть впечзтление, что с B мы будем иметь больший успех, чем с A. Поэтому мы переключаемся на исследование B. Мы стараемся ответить на вопрос: истинно B или ложно? В конце концов нам удается на него ответить. Какое влияние этот ответ оказывает на нашу уверенность в A?

Это зависит от ответа. Если мы находим, что B, это следствие A, ложно, то мы можем с достоверностью заключить, что и A должно быть ложно. Однако если мы найдем, что B истинно, то никакого доказательного умозаключения нет: хотя следствие B предположения A оказалось истинным, само A может быть ложным. Тем не менее имеется эвристическое умозаключение: так как следствие B оказалось истинным, само A заслуживает большей веры. В соответствии с природой нашего результата относительно B мы следуем

245

доказательной или эвристической схеме:

Доказательная	Эвристическая
Из A следует B	Из A следует B
B ложно	B истинно
A ложно	A более правдоподобно

Мы уже встречали эти схемы в § 12.1, где эвристическую схему мы назвали фундаментальной индуктивной схемой. С подобными же, но другими схемами мы познакомимся в следующих параграфах.

2. Исследование возможного основания. Рассмотрим другую ситуацию, часто встречающуюся в математических изысканиях. Мы хотим решить, истинно ли ясно сформулированное предложение A или нет, мы хотим доказать A или опровергнуть. После некоторой не имеющей решающего значения работы мы сталкиваемся с другим предложением B, из которого следовало бы A. Мы не знаем, истинно B или нет, но убедились, что

A следует из B.

Итак, если бы мы смогли доказать A, то было бы доказано и нужное нам A; A есть возможное основание для A. Мы могли устать от A или A может нам показаться более многообещающим, чем A; так или иначе мы переключаемся на исследование A. Наша цель теперь — доказать или опровергнуть B. В конце концов нам это удается. Какое влияние наш результат относительно B оказывает на нашу уверенность в A?

Это зависят от характера нашего результата. Если мы находим, что B истинно, то мы можем заключить, что A, которое следует из B, также истинно. Однако, если мы найдем, что B ложно, то никакого доказательного умозаключения нет: A могло бы еще оказаться истинным. Но мы были вынуждены отказаться от возможного основания для A, у нас теперь для доказательства A одним шансом меньше, наша надежда доказать A с помощью B рухнула: если вообще есть какое-нибудь изменение в нашей уверенности в A в результате опровержения B, то оно может быть только изменением к худшему. Короче, в соответствии с природой нашего результата относительно B мы следуем доказательной или эвристической схеме:

Доказательная	Эвристическая
Из A следует B	Из A следует B
B истинно	B ложно
A истинно	A менее правдоподобно

Следует заметить, что первая посылка в обеих схемах одинакова. Вторые посылки диаметрально противоположны, и заключения также противоположны, хотя и не столь уж далеки друг от друга.

246

Доказательное умозаключение следует классической схеме «modus ponens» так называемого гипотетического силлогизма. Эвристическая схема похожа на фундаментальную индуктивную схему, но отличается от нее, см. § 1 или § 12.1. Мы можем высказать это эвристическое умозаключение словами: Когда возможное основание для предположения рушится, наша уверенность в этом предположении может только уменьшиться.

3. Исследование противоречивого предположения. Рассмотрим ситуацию, не слишком обычную в математических изысканиях, но часто встречающуюся в естественных науках. Исследуем два противоречащих, несовместных предположения A в B. Когда мы говорим, что A противоречит B, или

A несовместно с B,

мы имеем в виду, что из истинности одного из двух предположений A и B необходимо следует ложность другого. Таким образом, A может быть истинно или нет, B также может быть истинно или нет, мы не знаем, что́ имеет место в действительности, но внаем лишь, что A в B не могут быть оба истинны. Однако оба они могли бы быть ложны. Натуралист, чтобы объяснить какое-то явление, высказал предположение A, другой натуралист, чтобы иначе объяснить то же самое явление, высказал предположение B. Объяснения несовместны; оба натуралиста не могут быть правы, но оба могут ошибаться.

Если доказано, что одно из этих предположений, скажем B, правильно, то и судьба другого окончательно решена: A должно быть ошибочно. Если, однако, B опровергнуто, то судьба A еще окончательно не установлена, и A могло бы оказаться ошибочным. Тем не менее бесспорно при опровержении соперничающего предположения, несовместного с A, A может только выиграть. (Натуралист, придумавший A, конечно, думал бы так же.) Таким образом, мы снова имеем две схемы:

Доказательная	Эвристическая
A несовместно с B	A несовместно с B
B истинно	B ложно
A ложно	A более правдоподобно

Когда рушится несовместное соперничающее предположение, наша уверенность в данном предположении может только возрасти.

4. Логические термины. В трех предыдущих параграфах мы встретили три пары схем. Каждая пара состоит из доказательной схемы и эвристической схемы; три доказательных схемы между собой связаны, и три соответствующие эвристические схемы кажутся соот-

247

ветствующим образом связанными. Связи между доказательными схемами — это ясные связи формальной логики. В следующем параграфе мы попытаемся выяснить связи между эвристическими схемами. Настоящий параграф подготовляет нас к следующему посредством обсуждения некоторых простых терминов формальной логики[91].

(1) Термин высказывание может быть взят в более общем смысле, но в нашем изложении чаще всего будет достаточно и даже выгодно думать о некотором ясно сформулированном математическом предложении, о котором в данный момент мы не знаем, истинно оно или нет. (Хорошим примером для более подготовленного читателя является знаменитая «гипотеза Римана»: ξ-функция Римана[92] имеет только действительные нули. Несмотря на усилия многих превосходных математиков, мы не знаем, истинно это высказывание или ложно.) Для обозначения высказываний мы будем пользоваться прописными буквами A, B, C, …

(2) Отрицание высказывания A есть высказывание, которое истинно в том и только в том случае, если A ложно. Отрицание A мы будем обозначать символом не-A.

13) Два утверждения «A ложно» и «не-A истинно» означают в точности одно и то же. В любом контексте мы можем подставить одно вместо другого, не изменяя значения, т. е. истинности или ложности, всего текста. Два утверждения, которые можно таким образом подставлять одно вместо другого, называются эквивалентными. Итак, утверждение «A ложно» эквивалентно утверждению «не-A истинно». Удобно записывать это в сокращенном виде:

«A ложно» экв. «Не-A истинно»[93].

Правильно также сказать, что

«A истинно» экв. «Не-A ложно»,

«Не-A истинно» экв. «A ложно»,

«Не-A ложно» экв. «A истинно»[94].[95]

(4) Мы говорим, что два высказывания A и B несовместны одно с другим, если они оба не могут быть истинны. Высказывание A может быть истинно или ложно, B может быть истинно или ложно;

248

если мы вместе рассмотрим и A и B, то могут возникнуть четыре различных случая:

A истинно, B истинно; A истинно, B ложно;

A ложно, B истинно; A ложно, B ложно.

Если мы говорим, что A несовместно с B, то мы подразумеваем, что первый из этих четырех случаев (в северо-западном углу) исключен. Несовместность всегда взаимна. Следовательно,

«A несовместно с B» экв. «В несовместно с A».

(5) Мы говорим, что A имплицирует B (илт B имплицируется A, или B следует нв A, или B является следствием A и т.д.), если A и не-B несовместны. Таким образом, понятие импликации[95] характеризуется следующей эквивалентностью:

«Из A следует B» экв. «A несовместно с не-B».

Знать, что из A следует B, важно. Пусть в данный момент мы не знаем, истинно A или нет, и в том же состоянии неведения находимся и по отношению к B. Если, однако, в какой-то момент окажется, что A истинно, то, располагая знанием, что и A следует B, мы немедленно будем знать, что не-B должно быть ложно и, таким образом, B должно быть истинно[96].

249

Мы знаем, что

«A несовместно с не-B» экв. «Не-B несовместно с A».

Мы знаем также, что

«Не-B несовместно с A» экв. «Из не-B следует не-A»[97].

Из цепи трех последних эквивалентностей заключаем:

«Из A следует B» экв. «Из не-B следует не-A»[98].

Эта последняя эквивалентность очень важна сама по себе и будет существенна в последующем рассмотрении.

(6) То немногое из формальной логики, что было изложено в этом параграфе, уже дает нам возможность выяснить связь между доказательными схемами, встретившимися нам в трех предыдущих параграфах.

Начнем с доказательной схемы, сформулированной в § 1«modus tollens»):

Из A следует B

B ложно

A ложно

Понятно, что эта схема всегда применима. Применим ее, подставив не-A вместо A и не-B вместо B. Получаем

Из не-A следует не-B

Не-B ложно

Не-A ложно

Мы видели, однако, рвньше, что

«Из не-A следует не-B» экв. «Ив B следует A»[99],

«Не-B ложно» экв. «B истинно»[100],

«Не-A ложно» экв. «A истинно»[101].[96]

Подставим вместо посылок и заключения последней рассмотренной схемы три соответствующих указанных здесь эквивалентных

250

утверждения. Тогда получаем:

Из B следует A

B истинно

A истинно

т. е. доказательную схему § 2, «modus ponens».

Мы предоставляем читателю подобным же образом вывести доказательную схему § 3 из схемы § 1.

5. Логические связи между схемами правдоподобных умозаключений. Рассмотрение в предыдущем параграфе было только подготовительным. Мы изложили эти классические вопросы доказательной логики не ради них самих, а чтобы приготовиться к изучению правдоподобных умозаключений. Мы рассмотрели вывод «modus ponens» на «modus tollens» не в какой-нибудь тщетной надежде сказать что-то новое и неожиданное относительно столь классических вещей, а для приготовления к таким вопросам, как например: можем ли мы с помощью чистой формальной логики вывести эвристическую схему § 2 из эвристической схемы § 1?

Нет, очевидно, не можем. В самом деле, эти схемы содержат такие утверждения, как «A становится более правдоподобным» или «A становится менее правдоподобным». Хотя каждый понимает, что это значит, последовательный формальный логик отказывается понимать такое утверждение, и он даже прав. В чистой формальной логике для таких утверждений нет места; она не имеет средств, чтобы с ними справиться.

Мы могли бы, однако, подходящим способом расширить область формальной логики. Главный пункт, по-видимому, — прибавление к классическому содержанию формальной логики следующей эквивалентности: «не-A становится более правдоподобным» экв. «A становится менее правдоподобным». Сокращенно

«Не-A более правдоподобно» экв. «A менее правдоподобно».

Допуская это, мы получаем полезный инструмент. Теперь мы можем приспособить прием § 4 (6) к нашей нынешней цели и поступить следующим образом. Мы начинаем с фундаментальной индуктивной схемы, приведенной в § 1. Применяем ее к не-A и не-B вместо применения ее к A и B, т. е. подставляем в нее не-A вместо A и не-B вместо B. Затем мы применяем три эквивалентности, две из которых являются чисто логическими (и изложены, кстати сказать, в предыдущем § 4), а третья — существенно новая эквивалентность, введенная в настоящем параграфе. С помощью этих трех шагов мы в конце концов приходим к эвристической схеме из § 2.

Можно предоставить читателю выписать этот вывод в деталях и таким же образом вывести эвристическую схему § 3 из фундаментальной индуктивной схемы § 1.

251

6. Затушеванное умозаключение. Мне кажется, что индуктивные рассуждения легче изучать в области математики, чем в области физики. Причина этого достаточно проста. Задавая математический вопрос, мы можем надеяться получить вполне недвусмысленный ответ, совершенно четкое Да или Нет. Направляя вопрос Природе, вы не можете надеяться получить ответ без некоторой полосы неопределенности. Вы предсказываете, что лунное затмение начнется (тень коснется диска луны) в такое-то и такое-то время. В действительности вы наблюдаете начало затмения 4 минутами позже, чем предсказано. Согласно стандартам греческой астрономии, ваше предсказание было бы поразительно точным, согласно современным стандартам оно скандально неточно. Данное расхождение между предсказанием и наблюдением можно истолковать и как подтверждение, и как опровержение. То или другое истолкование зависят от правдоподобного рассуждения некоторого рода, трудности которого в «физической ситуации» начинаются шагом раньше, чем в «математической ситуации». Мы попытаемся свести это различие к его простейшему выражению.

Допустим, что мы исследуем математическое предположение, рассматривая его следствия Пусть A обозначает предположение, а B — одно из его следствий, так что из A следует B. Мы приходим к окончательному решению относительно B: опровергаем B или доказываем и, соответственно, сталкиваемся с той или иной из следующих двух ситуаций:

Из A следует B	Из A следует B
B ложно	B истинно

Мы будем вх называть «математическими ситуациями». Мы их неоднократно рассматривали и внаем, что из каждой из них можно вывести разумное заключение.

Допустим теперь, что мы исследуем физическое предположение A и что мы экспервментзльно проверяем одно ва его следствий B. Относительно B мы не можем прийти к окончзтельному решению; наши эксперименты могут, однако, показать, что в B или в его противоположность очень трудно поверить. Соответственно мы сталкиваемся с той или иной ва следующих двух ситуаций:

Из A следует B	Из A следует B
B вряд ли правдоподобно	B почти несомненно

Назовем их «физическими свтуацвямв». Какое заключение разумно в этих ситуациях? (Пустое место под горизонтальной чертой, заменяющей слово «следовательно», символизирует открытый вопрос.)

В каждой из четырех рассмотренных ситуаций мы имели по две данных, или посылки. Первая посылка во всех четырех ситуациях одинакова; все различие между ними зависят от второй посылки. Вто-

252

рая посылка в «математических» ситуациях находится на уровне чистой формальной логики, но в «физических» ситуациях на значительно более смутном уровне. Это отличие мне кажется существенным; дополнительные трудности физических ситуаций могут им объясняться. Попытаемся обозреть эти четыре ситуации «путем последовательного и непрерывного движения мысли», как предпочитает говорить Декарт (см. эпиграф в начале этой главы). Представим себе, что наша уверенность в B постепенно изменяется, «непрерывно» уменьшаясь или увеличиваясь. Мы представляем, что B становится менее правдоподобным, затем еще менее правдоподобным, затем в него вряд ли можно поверить, и наконец оно становится ложным. С другой стороны, мы представляем, что B становится более правдоподобным, затем еще более правдоподобным, практически несомненным и, наконец, истинным[97]. Если сила нашего заключения непрерывно изменяется в том же самом направлении, что и сила нашей уверенности в B, то мало сомнений в том, каким должно быть наше заключение, с тех пор как ясны крайние случаи (B ложно, B истинно). Таким образом, мы приходим к следующим схемам:

Из A следует B	Из A следует B
B менее правдоподобно	B более правдоподобно
A менее правдоподобно	A несколько более правдоподобно

Слово «несколько» во второй схеме вставлено для того, чтобы напомнить нам, что заключение, конечно, является более слабым, чем в фундаментальной индуктивной схеме. Наша уверенность в предположении зависит от нашей уверенности в одном из его следствий и изменяется в том же направлении. Мы будем называть эти схемы «затушеванными»: первая — затушеванная доказательная схема, вторая — затушеванный вариант фундаментальной индуктивной схемы. Термин «затушеванная» должен указывать ослабление второй посылки: «менее правдоподобно» вместо «ложно», «более правдоподобно» вместо «истинно». Мы уже пользовзлись этим термином в этом смысле в § 12.6.

Мы получили только что введенные затушеванные схемы из их крайних случаев, «modus tollens» и фундаментальной индуктивной схемы, рассмотренных в § 1, ослабляя вторую посылку. Таким же образом мы можем получить другие затушеванные схемы из схем, сформулированных в § 2 и 3. Мы приведем здесь лишь одну (все они выписаны в следующем параграфе). Эвристическая схема § 3 дает следующую затушеванную схему:

253

7. Таблица. Чтобы сжато записать схемы, рассмотренные в этой главе, удобно воспользоваться некоторыми сокращениями. Мы пишем

A → B вместо из A следует B

A ← B вместо A следует из B

A | B вместо A несовместно с B

Введенные символы используются некоторыми авторами, пишущими по символической логике[102]. В этих обоаначениях две формулы

A → B, B ← A,

так же, как и формулы

A | B, B | A,

в точности эквивалентны. Мы будем также сокращать «правдоподобно» на «пр.» и «несколько» на «н.». См. табл. I.

Таблица I

	Доказательная (1)	Затушеванная доказательная (2)	Затушеванная индуктивная (3)	Индуктивная (4)
1. Исследование следствия	A → B B ложно A ложно	A → B B менее пр. A менее пр.	A → B B более пр. A н. более пр.	A → B B истинно A более пр.[103][98]
2. Исследование возможного основания	A ← B B истинно A истинно	A ← B B более пр. A более пр.	A ← B B менее пр. A н. менее пр.	A ← B[104] B ложно A менее пр.
3. Исследование противоречащего предположения	A | B B истинно A ложно	A | B[105] B более пр. A менее пр.	A | B[106] B истинно A н. более пр.	A | B[107] B истинно A более пр.

8. Комбинация простых схем. В математических изысканиях легко может возникнуть следующая ситуация. Мы исследуем теорему A. Эта теорема A ясно сформулирована, но мы не внаем и желаем уанать, истинна она или ложна. Когда пройдет некоторое время, мы наталкиваемся на возможное основание: мы видим, что A может быть выведено из другой теоремы H,

A следует из H,

и поэтому мы пытаемся доказать H. Доказать H нам не удается, но

254

мы замечаем, что одно из его следствий, B, истинно. Вот ситуация:

A следует из H

B следует из H

B истинно

Вытекает ли из этих посылок какое-нибудь разумное ззключение относительно A?

Я думаю, вытекает, и мы можем даже его получить, комбинируя две из схем, рассмотренных в предыдущем параграфе. Действительно, фундаментальная индуктивная схема дает:

Из H следует B

B истинно

H более правдоподобно

Чтобы получить это заключение, мы восползовались только двумя из трех посылок. Скомбинируем неиспользованную третью посылку с только что полученным заключением: одна из наших затушеванных схем (находящаяся на пересечении второй строки со вторым столбцом табл. 1 в § 7) дает:

A следует из H

H более правдоподобно

A более правдоподобно

Результат (как это и должно было быть) сам по себе довольно очевиден: увеличение уверенности в возможном основании H предложения A, возникающее в результате подтверждения следствия B этого основания H, в какой-то мере отражается и на самом A.

9. Об умозаключении по аналогии. Ситуацию, рассмотренную в предыдущем параграфе, можно истолковать как связь между схемами, рассмотренными в этой главе, и одной из наиболее бросающихся в глаза форм правдоподобного умозаключения: умозаключением по аналогии.

Я не думаю, что идею аналогии можно обьяснить во вполне определенных терминах формальной логики; во всяком случае, я на это не претендую. Как мы говорили ранее, в § 2.4, аналогия имеет дело со сходством и намерениями думающего. Если вы подмечаете между двумя объектами (или, предпочтительно, между двумя системами объектов) некоторое сходство и намереваетесь выразить эго сходство в определенных понятиях, то вы мыслите по аналогии.

Например, вы улавливаете некоторое сходство между двумя теоремами A и B; вы замечаете некоторые общие пункты. Быть может, вы думаете, что когда-нибудь будет возможно представить себе более

255

широкую теорему H, которая будет выявлять все существенные общие пункты и из которой и A и B будут естественно следовать. Если вы думаете таким образом, то вы начинаете мыслить по аналогии[108].

Как бы то ни было, рассмотрим аналогию между двумя теоремами A и B как намерение открыть общее основание, из которого следовали бы и A и B:

A следует из H, B следует из H.

Не будем забывать, что у нас нет H; мы только надеемся, что такое H существует.

Теперь нам удалось доказать одну из двух аналогичных теорем, скажем B. Как повлияет это событие на нашу уверенность в другой теореме A? У этой ситуации есть что-то общее с ситуацией, рассмотренной в предыдущем § 8. Там мы пришли к разумному заключению, выраженному составной схемой

A следует из H

B следует из H

B истинно

A более правдоподобно

Существует, конечно, важное отличие, состоящее в том, что теперь у нас нет H, мы только надеемся на H. С этой оговоркой, однако, мы можем рассматривать две посылки

A следует из H

B следует из H

как эквивалентные одной:

A аналогично B.

Подставляя эту одну посылку вместо первых двух посылок в написанную выше составную схему, приходим к фундаментальной схеме правдоподобного умозаключения, впервые указаной в § 12.4:

A аналогично B

B истинно

A более правдоподобно

10. Уточненное умозаключение. Возвратимся опять к фундаментальной индуктивной схеме. Это — первая введенная нами схема и наиболее бросающаяся в глаза форма правдоподобного рассуждения. Эта схема относится к подтверждению следствия из предположения

256

и получающемуся в результате изменению в нашем мнении. Она кое-что говорит о направлении этого изменения; такое подтверждение может только увеличить нашу уверенность в предположении. Она ничего не говорит о величине этого изменения; увеличение уверенности может быть большим или малым. В действительности оно может быть чудовищно большим и ничтожно малым.

Цель настоящего параграфа — выяснить обстоятельства, от которых зависит такое важное различие. Мы начинаем с напоминания об одном из примеров (§ 12.3).

Посудимый обвиняется во взрыве яхты отца своей приятельницы, и обвинение предъявляет расписку, подписанную подсудимым, подтверждающую покупку такого-то количества динамита.

Эта улика против подсудимого кажется очень сильной. Почему? Выделим главные черты этого случая. Существенную роль играют два утверждения:

A: Подсудимый взорвал эту яхту.

B: Подсудимый приобрел взрывчатое вещество.

В начале процесса суд должен рассматривать A как предположение. Обвинение стремится сделать A более правдоподобным для присяжных, защита старается сделать его менее правдоподобным.

В начале процесса и B тоже должно рассматриваться как предположение. Позднее, после представления в суд упомянутой расписки (подлинность подписи не оспаривалась защитой), B должно рассматриваться как доказанный факт.

Некоторые связи между A и B, однако, должны были быть ясны с самого начала.

A без B невозможно. Если подсудимый взорвал яхту, то у него было взрывчатое вещество. Он как-то приобрел это взрывчатое вещество: путем покупки, кражи, получения подарка, получения наследства или как-нибудь иначе, т. е.

Из A следует B.

B без A не невозможно, но с самого начала должно казаться крайне невероятным. Покупка динамита, во всяком случае, очень необычна для обыкновенного гражданина. Покупка динамита без намерения что-нибудь или кого-нибудь взорвать была бы бессмыслицей. Легко заподозрить, чго подсудимый имел весьма сильные эмоциональные и финансовые основания для взрыва этой яхты. Трудно подозревать какую-либо цель покупки динамита, исключая взрыв яхты. Таким образом, как мы сказали, B без A кажется крайне невероятным.

Особо выпишем эту важную характеристику ситуации: правдоподобность B до события, рассматриваемая при допущении, что A не истинно. Мы сократим это точное, но длинное описание так «правдоподобность B без A». Итак, мы можем сказать:

B без A едва ли правдоподобно.

257

Теперь мы можем видеть существенные посылки и всю схему правдоподобного умозаключения, которая производит на нас впечатление своей убедительностью:

Из A следует B

B без A едва ли правдоподобно

B истинно

A гораздо более правдоподобно

Чтобы лучше понять, представим себе, что эта важная характеристика ситуации, правдоподобность B без A, постепенно изменяется, непрерывно переходя от одного крайнего случая к другому.

Из A следует B. Если, наоборот, и из B следует A, так что A и B взаимно имплицируют друг друга, то правдоподобность B без A достигает своего минимума, исчезает. В этом случае, если B истинно, то и A достигает своего минимума.

Из A следует B, т. е. когда A истинно, B несомненно. Если правдоподобность B без A приближается к своему максимуму, то, когда A ложно, B почти несомненно. Следовательно, B в любом случае почти несомненно. Когда происходит событие, которое заранее кажется почти несомненным, мы не получаем много новой информации и, таким образом, не можем вывести неожиданных следствий. (Например, покупка буханки хлеба едва ли когда-нибудь может дать такую сильную улику, как покупка динамита.)

Допустим, как в § 6, что сила заключения непрерывно изменяется в одном и том же направлении, когда увеличивается или когда уменьшается этот имеющий большое влияние фактор: правдоподобность B без A. Тогда они должны изменяться в противоположных направлениях, и мы приходим к важному уточнению силы заключения в фундаментальной индуктивной схеме:

Из A следует B

B истинно

A более правдоподобно

Уточнение это состоит в том, что когда правдоподобность B без A уменьшается, сила заключения увеличивается.

Выпишем рядом два крайних случая:

{	Из A следует B B без A едва ли правдоподобно
B истинно
A гораздо более правдоподобно

258

{	Из A следует B B почти несомненно в любом случае
B истинно
A чуть-чуть более правдоподобно

Первые две посылки заключены в скобки[99], чтобы выразить, что вторая рассматривается как уточнение первой. То, что из A следует B, является первой посылкой в фундаментальной индуктивной схеме. Здесь мы уточняем эту посылку; мы добавляем уточнение, имеющее большое значение для определения силы заключения. Для сравнения вспомним, что в § 6 мы уточнили фундаментальную индуктивную схему в другом направлении, ослабив ее вторую посылку.

11. О последовательных подтверждениях. Мы уже подтвердили n следствий B₁, B₂, …, B_n некоторого предположения A. Теперь мы переходим к новому следствию B_n+1, проверяем его и находим, что и B_n+1 иет истинно. Какое влияние оказывает этот добавочный довод на нашу уверенность в A? Конечно,

Из A следует B_n+1

B_n+1 истинно

A более правдоподобно

Но насколько сильно это заключение? Это зависит, как мы видели в предыдущем параграфе, от правдоподобности B_n+1 без A.

Так вот, мы могли иметь хорошие основания верить в B_n+1 до того, как оно было подтверждено, даже при допущении, что A не истинно. Мы ранее видели, что B₁, B₂, …, B_n истинны. Если B_n+1 очень похоже на B_n+1, то мы можем по аналогии предвидеть, что и B_n+1 будет истинно. Если B_n+1 очень отличается от B₁, B₂, …, B_n, то оно не подкрепляется такой аналогией, и у нас может быть очень мало оснований верить в B_n+1без A. Следовательно, когда аналогия вновь подтвержденного следствия с ранее подтвержденными следствиями уменьшается, сила добавочной уверенности, возникающей в результате добавочною подтверждения, увеличивается.

Это, в сущности, выражает то же, что и дополнительные схемы, сформулированные в § 12.2, но, пожалуй, немножко лучше. В самом деле, явное упоминание об аналогии мы можем рассматривать как преимущество.

12. О соперничающих предположениях. Если существуют два различных предположения, A и B, предназначенные для объяснения одного и того же явления, то мы рассматриваем их как противодействующие одно другому, даже если не доказано, что они логи-

259

чески несовместны. Эти предположения A и B могут быть совместны или несовместны, но одно из них стремится сделать другое излишним. Это — достаточное противодействие, и мы рассматрнваем A и B как соперничающие предположения.

Бывают случаи, когда с соперничающими предположениями мы обращаемся почти так, как будто они несовместны. Например, мы имеем два соперничающих предположения A и B, но, несмотря на некоторое усилие, не можем придумать третьего предположения, объясняющего то же явление; тогда каждое зз двух предположений A и B является «единственным очевидным соперником» другого. Краткая схематическая иллюстрация может пояснить смысл этого термина.

Пусть, скажем, A — корпускулярная теория света, восходящая к Ньютону, B — волновая теория света, берущая начало от Гюйгенса. Представим также себе, что мы обсуждаем эти вопросы во времена после Ньютона и Гюйгенса, но до Юнга и Френеля, когда и в самом деле имело место очень неокончательное обсуждение этих теорий. Никто не показал или не претендовал на то, чтобы показать, что эти две теории логически несовместны, и еще менее, что они являются едиственными возможными логическими альтернативами; но не существовало никаких других теорий света, которые были бы достаточно известны, хотя физики имели широкую возможность изобретать такие теории: каждая теория была единственным очевидным соперником другой. Таким образом, любой аргумент, который казался говорящим против одной из двух соперничающих теорий, легко интерпретировался как говорящий в пользу другой.

Вообще, отношение между двумя соперничающими предположениями похоже на отношение между соперниками в любом другом виде соревнования. Если вы соревнуетесь на приз, то ослабление позиции любого из ваших соперников означает некоторое усиление вашей позиции. Вы немного выигрываете при легкой задержке одного из ваших многочисленных неясных соперников. Вы выигрываете много, если такая задержка случилась с опасным соперником. Вы выигрываете еще больше, если ваш наиболее опасный соперник выбывает из состязания. Если же вы имеете единственного очевидного соперника, то любое ослабление или усиление его позиции ощутимо сказывается на вашей позиции. И нечто подобное происходит между состязающимися предположениями. Существует схема правдоподобного рассуждения, которую мы попытаемся сделать несколько более ясной в табл. II.

Строение табл. II почти само собой понятно. Эта таблица содержит четыре схемы, расположенные в двух строках и двух столбцах. Первая строка содержит две уже рассмотренные схемы, см. § 3, конец § 6 и последнюю строку табл. I. Переходя от первой строки ко второй, мы ослабляем первую посылку; действительно, вместо ясной связи формальной логики между A и B мы подставляем

260

Таблица II

A несовместно с B B ложно	A несовместно с B B менее правдоподобно
A более правдоподобю	A несколько более правдоподобно
A соперник B B ложно	A соперник B B менее правдоподобно
A немного более правдоподобю	A чуть-чуть более правдоподобно

какую-то расплывчатую связь, имеющую, однако, практический смысл. Это ослабление первой посылки делает заключение соответственно слабее, что и пытается передать словесное выражение. Переходя от первого столбца ко второму, мы ослабляем вторую посылку, что делает соответственно слабее заключение. У схемы, находящейся в юго-восточном углу, нет ни одной посылки, которая имела бы смысл в доказательной логике, и ее заключение является самым слабым.

Важно подчеркнуть, что употребляемые словесные выражения слегка вводят в заблуждение. В действительности характеристики, прибавляемые к слову «правдоподобно» («несколько», «немного», «чуть-чуть»), должны были бы передавать не какую-то абсолютную, а только относительную степень правдоподобности. Они указывают только изменение силы, когда мы переходим от одной строки к другой, от одного столбца к другому. Даже наиболее слабая из этих четырех схем может давать весомое заключение, если убеждение, что предположение A не имеет другого опасного соперника, кроме B, достаточно сильно. Фактически эта схема будет играть некоторую роль в следующей главе.

13. О судебном доказательстве. Рассуждения, с помощью которых суд приходит к решению, можно сравнить с индуктивными рассуждениям, с помощью которых натуралист подкрепляет свои обобщения. Такие сравнения уже предлагались и обсуждались авторитетами по судебной процедуре[109]. Начнем обсуждение этого интересного вопроса с рассмотрения примера.

(1) Управляющий популярного ресторана, открытого допоздна, возвратился в свой загородный дом, как обычно, значительно позже полуночи. Когда он оставил автомобиль, чтобы открыть дверь своего гаража, он был остановлен и ограблен двумя субъектами в масках. Полиция, обследовавшая место происшествия, в палисаднике дома

261

жертвы нашла темно-серую тряпку. Эта тряпка могла быть использована одним из грабителей в качестве маски. Полиция допросила в близлежащем городе нескольких лиц. Один из допрошенных имел пальто с большой дырой в подкладке, но в остальном находившееся в хорошем состоянии. Тряпка, найденная в палисаднике, была из того же материала, что и подкладка, и в точности соответствовала дыре. Обладатель этого пальто был арестован и обвинен в участии в ограблении.

(2) Многие из нас, вероятно, почувствуют, что такое обвинение достаточно оправдывается обстоятельствами дела. Но почему? На какой идее это основано? Это обвинение является не изложением фактов, а выражением подозрения, выражением предположения:

A. Обладатель пальто участвовал в ограблении.

Такое официальное обвинение, однако, не должно быть беспричинным предположением, а должно подкрепляться относящимися к делу фактами. Предположение A подкрепляется фактом:

B. Тряпка, найденная в палисаднике дома жертвы ограбления, была из того же материала, что и подкладка пальто обвиняемого, и точно соответствовала дыре в подкладке.

Однако почему мы рассматриваем B как оправдание для A? Нам не следует забывать, что A — только предположение: оно может быть истинно или ложно. Если мы хотим поступать справедливо, мы должны рассматривать обе возможности.

Если A истинно, то B можно понять без труда. Мы легко можем себе представить, что человек, срочно нуждавшийся в маске и не имевший возможности достать более подходящий материал, отрезал кусок от подкладки своего пальто. Спеша удрать после преступного акта, такой человек мог потерять свою маску. Или в испуге он даже мог в тот же момент отбросить свою маску, вместо того чгобы положить ее в карман и бросить в безопасном месте. Короче, B вместе с A выглядит очень правдоподобно.

Если, однако, A не истинно, то B кажется необьяснимым. Если этот человек не был участником ограбления или чего-либо подобного, то зачем он должен был бы портить свое хорошее пальго, вырезая большой кусок из подкладки? И почему этот кусок подкладки из всех возможных мест должен был оказаться именно на месте грабежа, совершенного бандитами в масках? Он мог там оказаться конечно, и по-простому совпадению, но такому совпадению трудно поверить. Короче, B без A едва ли правдоподобно.

Итак, мы видим, что умозаключение, которое привело к обвинению обладателя пальто, имеет следующую схему:

{	B вместе с A весьма правдоподобно B без A едва ли правдоподобно
B истинно
A более правдоподобно

262

Но эта схема правдоподобного рассуждения очевидным образом связана с другой схемой правдоподобного рассуждения, которую мы разобрали раньше (в § 10):

{	Из A следует B B без A едва ли правдоподобно
B истинно
A гораздо более правдоподобно

Различие между этими двумя схемами проявляется уже в самом начале. Посылка

B вместе с A весьма правдоподобно

сходна с посылкой

Из A следует B

которая на самом деле может быть высказана и словами: «B вместе с A несомненно», но слабее, чем эта посылка. Итак первая схема (только что открытая) выступает как «ослабленная форма» второй схемы (введенной в § 10) и, таким образом, в конечном счете как уточнение фундаментальной индуктивной схемы (сформулированной в 2 12.1).

Случай, который привел нас к формулировке новой схемы, был довольно прост. Рассмотрим более сложный случай[110].

(3) К моменту убийства Клэренс Б. Хиллер со своей женой и четырьмя детьми жил в двухэтажном доме в Чикаго. Спальни семьи находились на втором этаже. На верхней площадке лестницы, ведущей на второй этаж, на ночь оставалась гореть газовая лампа. Вскоре после двух часов ночи с воскресенья на понедельник миссис Хиллер проснулась и заметила, что эта лампа погасла. Она разбудила мужа и он в ночной рубашке вышел на верхнюю площадку лестницы, где наткнулся на незнакомца. Они начали драться и во время драки скатились к основанию лестницы, где в Хиллера было сделано два выстрела; он умер через несколько секунд. Стрельба произошла приблизительно в 2 часа 25 мин. ночи.

За несколько минут до убийства одна из дочерей Хиллера в дверях своей спальни видела человека, державшего спичку так, что его лица нельзя было разглядеть. Она не испугалась потому, что отец обычно вставал ночью и проверял, все ли в порядке у детей. Никто другой из членов семьи постороннего не видел.

Приблизительно в трех четвертях мили от дома Хиллера имеется трамвайная остановка. Перед рассветом в день, когда произошло

283

убийство, четыре полисмена, у которых незздолго перед тем поблизости окончилось дежурство, сидели на скамье у этой остановки, ожидая трамвая. Примерно в 2 часа 38 мин. ночи они увидели человека, идущего в таком направлении, что скамья не могла быть ему хорошо видна. Когда человек приблизился, полисмены заговорили с ним, но он продолжал идти, держа правую руку в кармане. Полисмены остановили его и обыскали. В кармане был заряженный револьвер, человек вспотел, в разных местах его одежды выступала свежая кровь, на его левом предплечье была легкая рана, слегка кровоточащая. Полисмены (в то время не знавшие об убийстве) привели человека в полицейский участок, где он был допрошен. Этот человек — мы будем называть его подсудимым — позднее был обвинен в убийстве мистера Хиллера.

Суд должен был провести судебное следствие и после следствия отвергнуть или поддержать обвинение, т. е. следующее предположение, выдвинутое обвинительным актом:

A. Подсудимый стрелял в мистера Хиллера и убил его.

Сделаем обзор основных доводов, выдвигаемых в поддержку предположения A.

В₁. В двух гнездах барабана револьвера, найденного у подсудимого, когда он был арестован, имелся сгоревший порох и ощущался запах свежего дыма. По мнению полисменов, из револьвера дважды стреляли в пределах часа до ареста. Пять патронов, которыми был заряжен револьвер, имели в точности ту же фабричную марку, что и три нестреляных патрона, найденных в коридоре дома Хиллера поблизости от мертвого тела.

B₂. Незнакомец проник в дом Хиллера через ззднее окно кухни, с которого он сначала снял ставни. Человек, пролезающий через это окно, мог опереться на перила веранды. На этих перилах, которые были недавно покрашены, имелся отпечаток четырех пальцев левой руки. Два служащих бюро идентификации города Чикаго показали, что, по их мнению, отпечатки на перилах были тождественны отпечаткам пальцев подсудимого.

B₃. Два эксперта, не принадлежащие к чикагской полиции, выразили по поводу отпечатков пальцев то же мнение. (Один был инспектором полиции в Оттаве, Канада; другой — бывший эксперт Федерального правительства в Вашингтоне.)

B₄. Приблизительно в 2 часа 00 мин. ночи, как раз перед убийством мистера Хиллера, в дом, отделенный от дома Хиллера незанятым участком, проник неизвестный. Две женщины видели в дверях своей спальни человека с зажженной спичкой над головой. Обе женщины показали, что этот неизвестный был того же роста и телосложения, что и подсудимый. Одна из женщин вспомнила также, чго неизвестный был в светлой рубашке и с узорчатыми подтяжками. Осмотрев рубашку и подтяжки подсудимого, представленные в суд, свидетельница показала, что, по ее мнению,

264

подсудимый был тем человеком, которого она видела той ночью в дверях.

B₅. Подсудимый, когда он был арестован, назвал фальшивую фамилию и дал фальшивый адрес и отрицал, что он когда-либо находился под арестом. На самом деле он был ранее осужден по обвинению в краже со взломом, освобожден под честное слово, возвращен в каторжную тюрьму за нарушение честного слова и вторично освобожден под честное слово приблизительно за шесть недель до ночи убийства Примерно через две недели после второго освобождения он под фальшивой фамилией купил револьвер, отдал его в залог, получил обратно, заложил снова и вторично получил его обратно за два часа до убийства.

B₆. Подсудимый был не в состоянии удовлетворительно обьяснить ни кровь на своей одежде, ни рану на своем левом предплечье, ни свое местоприбывание в ночь убийства. Относительно своего местопребывания он рассказал две различные истории: одну после ареста, а другую в суде. Люди, которых, как он сначала утверждал, он посетил в ту ночь, отрицали это. Тогда подсудимый сказал суду, что он посетил салун, но не нашлось ни одного свидетеля, который подтвердил бы это.

(4) Все эти факты, события и обстоятельства, сообщенные под заголовками B₁, B ₂, …, B ₆, легко можно понять, если обвинение A справедливо. Все они подкрепляют A, но вес такого подкрепления не один и тот же во всех случаях. Некоторые из этих фактов были бы объяснимы, даже если бы A не было справедливо. Некоторые другие, однако, если бы A не было справедливо, казались бы сверхъестественными совпадениями.

То, что патроны, найденные в револьвере подсудимого, имеют ту же фабричную марку, что и патроны, найденные поблизости от тела жертвы, само по себе доказывает немногое, если патроны этой марки — обычные патроны, продаваемые всеми оружейными мастерами. Однако то, что из этого револьвера выстрелили ровно столько раз, сколько выстрелов было сделано в жертву, и в пределах того же часа, доказывает многое; трудно объяснить такое совпадение. Совпадение отпечатков пальцев на перилах с отпечатками пальцев подсудимого в наше время и само по себе рассматривалось бы как почти решающее доказательство, но еще не рассматривалось так в то время, когда происходил суд, в 1911 г. То, что обвиняемый лгал относительно своей фамилии, адреса и преступного прошлого, когда он был арестован, доказывает немногое: такую ложь можно понять, если обвинение A справедливо, но можно понять и если оно несправедливо: человек во всяком случае предпочел бы, чтобы полиция оставила его в покое. Однако значительный вес имеет то, что подсудимый был не в состоянии удовлетворительно объяснить свое местопребывание в эту роковую ночь. Он должен был знать, что этот вопрос важен, и его защитник, несомненно, знал о важ-

265

ности любого алиби. Если обвинение A было ложно и подсудимый провел ночь, не причинив никому вреда, или совершил какое-нибудь меньшее преступление, то почему он не сказал этого сразу же или по крайней мере до того, как стало слишком поздно?

Все упомянутые подробности легко можно понять, если обвинение A справедливо. Но совпадение такого большого числа подробностей кажется необъяснимым, если обвинение A А несправедливо: крайне трудно поверить, что столько совпадений произошло только по простой случайности. Как бы то ни было, защите не удалось представить состоятельного толкования предъявленных улик.

Для присяжных были, конечно, и другие улики, помимо тех, о которых мы здесь рассказали, и были улики, которые нельзя точно передать никаким описанием: поведение подсудимого и свидетелей. Присяжные признали подсудимого виновным в убийстве, и Верховный суд штата подтвердил приговор. Приведем последнюю фразу из мнения Главного судьи: «Ни одно из этих обстоятельств, рассматриваемое отдельно, не было бы решающим для установления его (подсудимого) вины, но когда все факты и обстоятельства, входящие в число улик, рассматриваются вместе, можно найти оправдание присяжным, которые были уверены, что вердикт о виновности должен последовать как логическое следствиев[111].

(5) Утверждения B₁, B ₂, …, B ₆, перечисленные в (3), довольно хорошо соответствуют схеме, введенной в (2). Они даже лучше соответствуют схеме, отличающейся от нее только в одном пункте:

{	B вместе с A весьма правдоподобно B без A не в такой степени правдоподобно
B истинно
A более правдоподобно

Каждое из утверждений B₁, B ₂, …, B ₆, может быть с полным смыслом подставлено в эту схему вместо B, причем, конечно, A должно интерпретироваться как обвинение. Утверждения B₁, B ₂, …, B ₆, являются составными утверждениями; они имеют части (некоторые из них мы подчеркнули в (4)), каждая из этих частей сама по себе может рассматриваться как существенная улика: каждая такая часть также с полным смыслом может быть подставлена вместо B в приведенную выше схему. Если мы вспомним наш разбор в (4), то, конечно, сможем ясно понять, что чем менее правдоподобно B без A, тем сильнее заключение.

Если мы ясно представим себе, как свидетели один за другим подтверждали перед присяжными на протяжении пропесса множество улик, то мы сможем яснее увидеть, что правдоподобные

266

рассуждения в таких процессах и в научном исследовании, в котором последовательно проверяется несколько следствий из предположения, играют аналогичную роль (ср. особенно § 12.2).

(6) Предыдущее рассмотрение ясно подсказывает составную схему правдоподобного рассуждения, имеющую к схеме, сформулированной в (5), в точности такое же отношение, какое составная схема, введенная в § 12.2, имеет к фундаментальной индуктивной схеме § 12.1. Я не вхожу здесь в этот предмет; читатель, более сведущий в доктрине судебного доказательства, мог бы разработать его с более выразительными примерами и интерпретациями, но я прибавлю еще одну иллюстрзпию этой схемы.

Когда Колумб и его товарищи плыли на запад через неведомый океан, они всякий раз, когда видели птиц, приветствовали их громкими возгласами. Они рассматривали птиц как благоприятный признак, указывающий на близость земли. Хотя в этом они неоднократно бывали разочарованы, лежащее в основании рассуждение мне кажется совершенно правильным. Если сформулировать это рассуждение со всеми подробностями, то оно будет звучать следующим образом:

{	Когда судно близко к земле, мы часто видим птиц. Когда судно далеко от земли, мы видим птиц реже.
Теперь мы видим птиц.
Следовательно, то, что мы близко к земле, становится более правдоподобным.

Это рассуждение в точности соответствует схеме, сформулированной в (5): присутствие птип рассматривается как косвенная улика в пользу близости земли. Спутники Колумба видели нескольких птип в четверг, 11 октября 1492 года, а на следующий день был открыт первый остров Нового Света.

Читатель может заметить, что проиллюстрированная схема лежит в основании многих из наших каждодневных рассуждений.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ XIII

Первая часть

1. Следуя методу § (4) 6, выведите доказательную схему, упомянутую в § 3, из доказательной схемы, упомянутой в § 1.

2. Восполните детали доказательства, намеченного в § 5: выведите эвристическую схему § 2 из эвристической схемы § 1.

3. Выведите эвристическую схему § 3 из эвристической схемы § 1.

4. В кроссворде нам нужно найти слово из 8 букв, и вот к нему ключ: «неприягная форма верности»[112][100].

257

Условие, которому должно удовлетворять неизвестное слово, конечно, высказано двусмысленно. После нескольких неудачных попыток мы можем подметить, что «верность» состоит из восьми букв, как раз из стольких, из скольких состоит и неизвестное слово, и зто может привести нас к следующему предположению:

A. Неизвестное слово означает «неприятное» и является анаграммой слова ВЕРНОСТЬ.

(Анаграмма данного слова — зто слово, составленное из тех же букв, но расположенных в другом порядке.) Это предположение A может казаться весьма вероятным. (Действительно, слова «форма верности» могут наводить на мысль, что на кроссвордном жаргоне речь идет об анаграмме слова «верность»[101].) Стараясь отгадать другие неизвестные слова кроссворда, мы находим вполне правдоподобные решения для двух из них, пересекавших упомянутое восьмибуквенное слово, для которого мы получаем две возможные буквы, расположенные как указаю на следувщей диаграмме:

— — В — — — Т—

Мы можем рассматривать это как довод в пользу нашего предположения A.

(a) Почему? Укажите соответствувщув схему.

(b) Попытайтесь найти требуемое восьмибуквенное слово. [Отыскивая зто слово, вы имеете естественнув возможность оценить вес зтого довода в пользу А. Вот несколько наводящих вопросов: Где наиболее вероятно должен стоять Ь? Куда можно было бы поставить гласные Е и О? См. также Как решать задачу, стр. 79 — 81.]

5. Возвратимся еще раз к судебному случав, уже рассмотренному в § 12.3 и (более полно) в § 10. Рассмотрим снова обвинение [Factum Probandum, факт, который должен быть доказан обвинителем):

A. Подсудимый взорвал яхту.

Однако изменим утверждение B и в качестве B рассмотрим здесь утверждение:

B. Подсудимый купил динамит в такой-то лавке, в такой-то день.

Изменение состоит в том, что В обозначает теперь не общее утверждение, а конкретный факт. [Суд предпочитает или должен был бы предпочитать иметь дело с фактами как можно более точными.) Примем B за доказанное. [Итак, B есть Factum Probandum — факт, подкрепленный доказательством.)

Изменение утверждений, которое мы произвели, не может изменить силу аргументации. Но какова теперь схема?

6. Подсудимые — подрядчик и государственный чиновник. Один обвиняется в том, что дал, а другой в том, что взял взятку.

Обвинение носит конкретный характер: обвинительный акт утверждает, что плата наличными за новый автомобиль чиновника была произведена из кармана подрядчика. Одним из свидетелей обвинения был торговец автомобилями; он показал, что к 29 ноября получил 675 долларов как плату за автомобиль чиновника[102]. Другим свидетелем был управлявший местным банком; он показал, что 27 ноября (того же года) с обычно бездействувщего общего счета подрядчика и его жены было выдано 675 долларов; расписка была подписана женой. Эти факты не оспаривались защитой.

Что вы рассматривали бы как сильный пункт зтих улик? Назовите подходящув схему.

7. Черные, Белые и Зеленые жили на одной и той же улице в Пригородске. Черные и Белые были соседями, а Зеленые жили как раз напротив. Однажды вечером мистер Черный и миссис Белая вели через изгородь продолжительный разговор. Было довольно темно, однако миссис Зеленая не преминула понаблюдать за этим разговором и сделать поспешное заключение — вы знаете, какое заключение: излюбленное предположение миссис Зеленой.

К несчастью, едва ли удастся остановить поток сплетен, начало которому положила миссис Зеленая. Если, тем не менее, взяв на себя страшный риск,

268

вы пожелаете образовать в своем лице совет для зашиты невинных людей, оклеветанных миссис Зеленой, я могу сообщить вам факт: Белые, которые уже давно хотели переехать поближе к конторе мистера Белого, подписали договор об аренде дома, принадлежащего дяде мистера Черного, и зто произошло через несколько дней после упомянутой беседы. Воспользуйтесь зтим фактом.

В чем состоит ваша защита и какова схема?

8. Обвинение пытается доказать:

A. Подсудимый знал и был способен узнать жертву во время совершения преступления.

Обвинение подкрепляет зто неоспоримым фактом:

C. И подсудимый и жертва за три года до совершения преступления в течение нескольких месяцев работали в одной и той же фирме.

Итак, A есть Factum Probandum, а C выдвигается в качестве Factum Probans. Какова схема? [Обозначения придуманы так, чтобы вам помочь. Играет ли какую-нибудь роль величина фирмы?]

9. Об индуктивном исследовании в математике и в физических науках. В § 6 было указано различие между «математической ситуацией» и «физической ситуацией», которое кажется важным с точки зрения правдоподобных рассуждений. По-видимому, существуют и другие различия этого рода, и одно из них будет рассмотрено здесь.

Кулон открыл, что сила взаимодействия между электрическими зарядами изменяется обратно пропорционально квадрату расстояния. Он подкрепил зтот закон обратного квадрата прямыми экспериментами с крутильными весами. Эксперименты Кулона были деликатными, и расхождение между его теоретическими и экспериментальвыми числами было значительным. Мы не можем удержаться от подозрения, что без мощной аналогии закона Ньютона [закона обратного квадрата в гравитационном притяжении) ни сам Кулон, ни его современники не рассматривали бы его зксперименты с крутильными весами как окончательные.

Кавендиш открыл закон обратного квадрата в злектрическом притяжении и отталкивании независимо от Кулона. (Исследования Кавендиша не были опубликованы при его жизни, и приоритет Кулона неоспорим.) Однако Кавендиш, чтобы подкрепить зтот закон, придумал более тонкий эксперимент. Нам нет необходимости входить в детали его метода[113], только одна особенность которого здесь существенна: Кавендиш учитывает возможность того, что сила пропорциональна не r^–2 (r — расстояние между электрическими зарядами), а общее, r^–α, где α — некоторая положительная постоянная. Его эксперимент показал, что число α — 2 по абсолютной величине не может превосходить некоторой дроби.

Экспериментальное исследование Кулона довольно похоже на индуктивное исследование в математике: он сопоставляет частные следствия из предполагаемого физического закона с наблюдениями, как математик сопоставлял бы с наблюдениями частные следствия из предполагаемого теоретико-числового закона. И здесь, и там важную роль в выборе предполагаемого закона может играть аналогия. Однако экспериментальное исследование Кавендиша имеет иной характер; он рассматривает не один лишь предполагаемый закон (закон r^–2), а несколько предполагаемых законов (законы r^–α). Эти законы различны (различные законы злектрического притяжения соответствуют различным значениям параметра α), но они родственны, они принадлежат одному «семейству» законов. Кавендиш сопоставляет с наблюдениями все семейство законов и пытается подобрать закон, который лучше всего с ними согласуется.

Это — наиболее характерное различие между двумя исследованиями: первое направлено на одно предположение, второе — на семейство предположений. Первое сравнивает наблюдения со следствиями одного предположения, второе

269

одновременно сравнивает их со следствиями нескольких предположений. Первое пытается на основании такого сравнения судить, приемлемо ли предлагаемое предположение или нет, второе пытается отыскать наиболее приемлемое (или наименее неприемлемое) предположение. Первый вид индуктивного исследования широко практикуется в математике и не является необычным в физических науках. Второй вид индуктивного исследования широко практикуется в физических науках, но мы очень редко встречаемся с ним в математике.

Фактически, наиболее типичный вид физического эксперимента имеет целью измерение какой-нибудь физической константы, определение ее значения, как эксперимент Кавендиша имел целью определение значения показателя степени α. В математике встречаются такие изыскания, которые мы могли бы рассматривать как индуктивное исследование, имеющее целью определение какой-нибудь математической константы, но такие исследования являются совершенно исключительными[114].

10. Пробные общие формулировки. Часто повторявшиеся Ньютоном слова: «Hypotheses non fingo»[115], несколько односторонни. Было бы ошибкой истолковать их, как «Остерегайтесь предположений»: такой совет, если ему следовать, погубил бы индуктивное исследование. Вот лучший совет: быстро создавай предположения, медленно их принимай. Еще лучше слова Фарадея: »Философ должен быть человеком, который готов выслушать любой совет, но полон решимости судить самостоятельно». Конечно, философ, которого имеет в виду Фарадей, занимается экспериментальной[116], а не традиционной философией.

Мы собираемся сейчас «индуктивно» исследовать правдоподобные рассуждения. Я изложу здесь не стесняясь несколько пробных обобщений. Они относятся к немногим формам правдоподобных рассуждений, но читателю нужно иметь в виду, что перед любой попыткой дальнейшего распространения зтих форм следует тщательно обдумать сначала самую их формулировку.

(1) Монотонность. Рассмотрения § 6 могут натолкнуть на мысль о правиле: «Заключение правдоподобного умозаключения монотонно изменяется, когда монотонно изменяется одна из его посылок». Это соответствует случаю, рассмотренному в § 6, и еще нескольким случаям, часть из которых будет вскоре рассмотрена.

(2) Непрерывность. Нам понадобится один термин доказательной логики. Мы говорим, что

A и B равнозначны,

если A и B взаимно имплицируют друг друга, т. е. если A следует из B и, также, B следует из A. Если A и B равнозначны, то мы можем в данный момент не знать, истинны ли A и B, но мы знаем, что возможны только два случая: или оба они истинны, или оба ложны; A и B стоят или рушатся вместе. Вот наглядное символическое выражение для равнозначности A и B:

A ↔ B[103].

Две стрелки указывают, что мы можем от истинности любого из двух утверждений A и B перейти к истинности другого.

В § 10 мы рассмотрели наводящую на новые мысли связь между двумя утверждениями A и B. Мы рассмотрели логическое отношение

Из A следует B

270

совместно с правдоподобностью B без A. Представим себе, что эта правдоподобность монотонно изменяется: B без A становится все менее и менее правдоподобным. B пределе, когда B без A становится невозможным, из истинности B следует истинность A. Однако мы допустили, что из истинности A следует истинность B, и, таким образом, в пределе A и B взаимно имплицируют друг друга, становятся равнозначными.

Понаблюдаем теперь, как описанное изменение действует на фундаментальную индуктивную схему:

Из A следует B

B истинно

A более правдоподобно

Допустим, что пока первая посылка изменяется, как описано выше, вторая посылка остается неизменной. Когда B без A становится все менее и менее правдоподобным, предположение A в результате подтверждения его следствия B становится все более и более правдоподобным. Иными словами, заключение становится сильнее, вес его увеличивается. В пределе заключение превратится в «A истинно», и, таким образом, наша схема правдоподобного умозаключения станет в пределе следующей (очевидной) схемой доказательного умозаключения:

A и B равнозначны

В истинно

A истинно

Короче, наша схема правдоподобного умозаключения имеет «предельную форму», являющуюся схемой доказательного умозаключения. Когда посылки правдоподобного умозаключения «стремятся» к соответствующим посылкам предельной формы, правдоподобное заключение «приближается» к своей наибольшей предельной силе. Еще короче: от эвристической схемы к доказательной схеме существует непрерывный переход.

Бо́льшая часть этого описания соответствует и ряду других случаев. Некоторые из них показаны в табл. III. В табл. III употребляются символика и обозначения, введенные выше. Мы пользуемся также объясненным выше символом ↔. Вместо не-B, определенного в § 4, применяется более короткий символ B.

Таблица III

Допредельный	A → B B истинно A более пр.	A → B B истинно A н. более пр.	A | B B ложно A более пр.	A | B B менее пр. A н. более пр.
Предельный	A ↔ B B истинно A истинно пр.	A ↔ B B более пр. A более пр.	A ↔ ͞B B ложно A истинно	A ↔ ͞B B менее пр. A более пр.

(3) Правдоподобное из доказательного? Таблица III может натолкнуть нас и на другую мысль. Предельные схемы в этой таблице более очевидны, чем допредельные. Две из этих предельных схем являются доказательными, а две другие, хотя и не являются чисто доказательными, едва ли могут вызывать сомнение. Более спорные допредельные схемы, все являющиеся схемами правдоподобных умозаключений, по-видимому, возникают из соответствующих предельных схем путем равномерного процесса «ослабления»: более сильные утверждения, как например

A ↔ B, A истинно, A более пр.

271

систематически заменяются соответствующими более слабыми утверждениями, как например

A → B, A более пр., A н. более пр.

Не могут ли быть все формы правдоподобного умозаключения каким-нибудь аналогичным образом связаны с формами доказательного или почти доказательного умозаключения?

Вторая часть

Пример 11 следует прочитать вначзле: он вводит (и извиняет) последующее.

11. Более личное, более сложное. Ранее я не подвергал обсуждению предположения из моих собственных опубликованных математических работ. Это упущение, так как в конце концов ни одного математика я не могу знать ближе, чем самого себя. Это упущение могло бы даже некоторым читателям показаться подозрительиым. Я не думаю, что такое подозрение оправдано. Причиной, по которой я не говорил о более сложных специальных вопросах из моих собственных исследований, является не недостаток откровенности, а именно сложность и специальность этих вопросов; я думал, что лучше обсуждать более простые вопросы, имеющие более общий интерес.

Нижеследующие примеры 12—19 предполагают значительно более высокий уровень знаний, чем бо́льшая часть книги. Они взяты из моих собственных исследований. Я пытаюсь предложить характерные образцы. Я включаю несколько предположений, которые уже появлялись в печати, и несколько еще не опубликованных. Я включаю несколько предположений из моих «наивных» ранних работ, когда я еще не начинал в явной форме думать на тему о правдоподобных рассуждениях, и предположения из более поздних, менее наивных работ. Пример 12 относится к моим наивным дням; он рассказывает об эвристических основаниях, которые привели меня к одному результату. Примеры 13, 14, 15 и 16 касаются ранее опубликованных предположений из моих наивных лет, пример 17 — ранее опубликованного предположения из моих менее наивных лет, а примеры 16 и 19 — предположений, которые до сих пор не бьыи опубликованы[117].

Должен прибавить, что даже в мои наивные годы меня поражала и несколько озадачивала сила уверенности, которую вселяли в меня мои собственные предположения, и я недоумевал, какого рода причины могли бы лежать в основании такой уверенности. Следующие слова довольно хорошо выражают мои ранние взгляды на источник новых предположений.

«Существует прямая, соединяющая две данные точки. Новая теорема часто является обобщением, соединяющим два крайних случая, и получается путем своего рода прямолинейной интерполяции. Существует прямая, проходящая через данную точку в данном направлении. Новая теорема часто возникает в счастливый момент, когда общее направление исследования встречается с

272

подходящим частным случаем. Новая теорема может также явиться результатом проведения параллели[118].

12. _Существует прямая, соединяющая две данные точки. Числа A_n^(k), расположенные в виде бесконечного квадрата,

связаны с функцией f(x). (Они выводятся из разложения f(x) по степеням x; A_n^(k) и f(x) предполагаются действительными.) Э. Лагерр открыл, что V(k), число перемен знака в k-ой строке, A₀^(k), A₁^(k), A₂^(k), …, таблицы связано с R, числом корней уравнения f(x) = 0, находящихся между 0 и 1 (границы исключаются):

V(k) ≥ R,

и когда k растет, V(k) может только убывать или оставаться постоянным. Не достигнет ли в конце концов R никогда не возрастающее V(k)? Лагерр пред-

ложил этот вопрос, но оставил его неразрешенным. М. Фекете доказал, что если R = 0, то V(k) в конечном счете достигает R, и этот частный случай подсказывает предположение, что V(k) всегда достигает R. Мне настолько повезло, что я подметил другую связь между числами A_n^(k) и функцией f(x): существуют некоторые положительные числа B_n^(k) (не зависящие от функции f(x)), такие, что

т. е. вертикальное направление в бесконечной квадратной таблице связано с f(0), горизонтальное — с f(1). Эти два крайних направления, вертикальное и горизонтальное, могут напомнить вам две крайние точки, которые требуется соединить: что можно сказать о промежуточных наклонных направлениях? Только на мгновение примите предположение, которое мы хотим доказать, без доказательства: оно[104] влечет за собой некоторую связь между промежуточными направлениями и значениями, которые принимает f(x), когда x изменяется между 0 и 1. Это наводит на мысль, что A_n^(k)/B_n^(k) может стремиться к f(x), где x как-то связан с пределом n/k. В самом деле, я в конечном счете нашел, и зто даже было легко доказать, что

Это соотношение оказалось ключом к решению задачи Лагерра.

13. Существует прямая, проходящая через данную точку в данном направлении. Проведение параллели. В связи с рядом Фурье положительной функции f(x):

273

О. Тёплиц рассмотрел уравнение относительно λ

a0 — λ a1 — ib1 … an-1 — ibn-1 a1 + ib1 a0 — λ … an-2 — ibn-2 ................................... an — 1 + ibn-1 a n-2 + ibn-2 … a0 — λ

= 0.

(*)

Его исследование обнаружило, что n корней этого уравнения

λ_n1, λ_n2, λ_n3, …, λ_nn

«имитируют» n равноотстоящих значений функции f(x)

Например, среднее арифметическое n корней

соответствует пределу

Попытаемся провести параллель: среднее геометрическое n корней

где D_n обозначает определитель n-го порядка, который мы получаем, полагая λ = 0 в левой части уравнения (*). Оно может соответствовать пределу

(**)

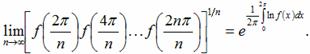На этом этапе естественно поискать удобный частный случай. Для частной функции

f(x) = a₀ + 2a₁ cos x + 2b₁ sin x

нетрудно вычислить D_n и и этот предел оказывается равным значению «**»): общее направление исследования встретилось с подходящим частным случаем, и было бы трудно не высказать предположение: для любой положительной функции f(x)

.

14. Наиболее очевидный случай может оказаться единственным возможным случаем. Если коэффициенты a₀, a₁, a₂ …, a_n, …, степенного ряда

a₀ + a₁z + a₂z² + … + a_nzⁿ + …

являются целыми числами, среди которых бесконечное множество отлично от

274

0, то, очевидно, в точке z = 1 ряд расходится, так как его общий член не стремится к 0. Следовательно, радиус сходимости такого степенного ряда ≤ 1. Крайнее значение 1 радиуса сходимости может достигаться. Очевидный пример — ряд

1+ z + z² + ... + zⁿ + …;

он представляет функцию крайне простого аналитического характера, рациональную функцию 1/(1 — z). Вот другой пример:

z + z² + z⁶ + ... + z^n! + …;

он представляет функцию крайне сложного аналитического характера, непродолжаемую функцию.(Это наиболее обычный пример ряда, для которого граница круга сходимости является особой линией.) Эти два очевидных примера являются примерами функций противоположной природы. Однако, удивительным образом, любой степенной ряд с целыми коэффициентами и радиусом сходимости 1, аналитическую природу которого эффективно можно установить, оказывается похожим на один из этих двух противоположных примеров: он представляет или рациональную функцию, или непродолжаемую функцию. Теоремы Э. Бореля и П. Фату показывают, что обширные классы функций промежуточной природы не могут быть представлены таким рядом. Когда автору удалась доказать подобные же теоремы и справиться с многими примерами, он извлек установочные доводы для гипотезы: «Наиболее простые продолжаемые аналитические функции, представляемые степенным рядом с целыми коэффициентами и радиусом сходимости 1, функции, заведомо рациональные, являются единственными такими функциями». Иными словами, «Если радиус сходимости степенного ряда с целыми коэффициентами достигает крайнего значения 1, то представляемая им функция необходимо является функцией крайнего характера: она — крайне простая, рациональная функция или крайне сложная, непродолжаемая функция».

15. Установление моды. Сила слов. Этот пример имеет различные аспекты, которые я попытаюсь изложить один за другим.

(1) Э. Лагерр открыл несколько последовательностей действительных чисел

α₀, α₁, α₂, …, α_n,

обладающих следующим любопытным свойством: если (в остальном произвольное) уравнение степени n

a₀, + a₁x + a₂x² + … + a_nxⁿ = 0 (I)

имеет только действительные корни, то и уравнение

a₀α₀, + a₁α₁x + a₂α₂x² + …+ a_nα_nx = О (II)

(в которое наша последовательность a₀, ..., a_n преобразует (I)) будет иметь действительные корни. Лагерр предложил, но оставил нерешенной задачу: найти простое необходимое и достаточное условие, характеризующее последовательности этого рода.

Легко найти необходимые условия: просто применим последовательность желаемого рода к любому уравнению, про которое известно, что оно имеет только действительные корни, и тогда получим преобразованное уравнение, все корни которого необходимо являются действительными. Например, применяя последовательность α₀, α₁, …, α_n к уравнениям

1 — x = 0, x² — x⁴ = 0, x⁴ — х⁶ = 0, …,

имеющим, очевидно, только действительные корни, легко находим, что числа α₀, α₂, α₄, α₆, … необходимо[105] одного знака, все они положительны или все отрицательны (в широком смысле: 0 не исключается). Применяя ту же последователыюсть к уравнениям

1 — x³ = 0, x³ — x⁵ = 0, x⁵ — х⁷ = 0, …,

275

находим, что и числа α₁, α₃, α₅, α₇, … необходимо одного знака. Используя эти замечания и применяя последовательность к уравнению

(III)

(все n корней которого равны — 1), получаем необходимое условие, что все корни уравнения

являются действительными и имеют одинаковый знак.

Мы получили это последнее условие путем накопления необходимых условий. Их должно было накопиться уже довольно много; но настольно ли много, чтобы образовать достаточное условие? Если бы это было так, то имело бы место следующее любопытное предложение: «Если оба уравнения (I) и (IV) имеют только действительные корни, и все корни уравнения (IV) одного знака, то и уравнение (II) имеет только действительные корни».

(2) Это предположение пришло мне в голову довольно рано, но я не мог в него поверить: оно выглядело слишком странно. Однако в случае n = 2 предположение легко подтвердилось (случай n = 1 совершенно тривиален).

Позднее случайно я наткнулся на теорему, доказанную Мало́: Если уравнение (I) имеет только действительные корни, а уравнение

a₀, + a₁x + a₂x² + … + a_nxⁿ = 0

имеет только действительные корни одного знака, то уравнение (II) должно иметь только действительные корни. Теорема Мало́ была явно аналогична этому странному предположению, и в результате оно стало казаться значительно менее странным. Более того, теорема Мало́, в чем я легко смог убедиться, была следствием этого предположения, и, таким образом, подтвердилось еще одно широкое и важное следствие предположения: это предположение стало казаться намного более сильным[106].

(3) Как легко видеть, это предположение следующим образом можно высказать иначе: «Если последовательность положительных чисел α₀, α₁, …, α_n преобразует уравнение (III) в уравнение, имеющее только действительные корни, то произвольное уравнение, имеющее только действительные корни, оно преобразует в уравнение той же природы». Другими словами, уравнение (III) устанавливает моду: его отклику на последовательность α₀, α₁, …, α_n подражают все уравнения, все корни которых действительны.

(4) Почему уравнение (III) устанавливает моду? Потому что все его корни совпадают. Этот ответ в каком-то смысле является «правильным» ответом. Во всяком случае, как я обнаружил позднее, уравнения (или функции), все корни (или нули) которых совпадают, в нескольких аналогичных задачах играют аналогичную роль: они устанавливают моду (они являются «tonangebend»[119]).

Однако когда рассматриваемое предположение было еще предположением, я прибег к следующему «объяснению». Все корни уравнения (III) равны — 1. Все эти корни стиснуты в одной точке действительной оси, они так близки друг к другу, как это только возможно. В такой ситуации они, понятно, наиболее склонны выпрыгнуть из действительной оси. Поэтому если последовательности α₀, α₁, …, α_n, когда она[107] применяется к многочлену (1 + x)ⁿ с наиболее стиснутыми корнями, не удается выбить из действительной оси эти корни, то она имеет еще меньше шансов выбить менее стиснутые корни других многочленов.

Логическая ценность этого «объяснения», очевидно, равна нулю, но из этого не следует, что равна нулю и его психологическая ценность. Я убежден, что эта

276

шутливая аналогия лично для меня была крайне важна: она помогла сохранить предположение живым в течение многих лет[108].

Мне следуетздесь упомянуть, что подобные необычные словесные формулировки часто связаны с моей математической работой. Характерный пример — сентенция, приведенная в конце примера 14. Вот еще два примера.

В течение более чем двух десятилетий я очень интересовался хорошо известной теоремой Фабри о пропусках в степенны́х рядах[120]. Было два периода: первый «созерцательный» период и второй «активный» период[109]. В активный период я делал некоторую работу, связанную с этой теоремой, и нашел различные доказательства. Обобщения и аналоги к ней. В созерцательный период я практически не делал никакой работы, связанной с теоремой, я только любовался ею и время от времени вспоминал ее в несколько забавной, притянутой за волосы, формулировке вроде: «Если бесконечно невероятно, чтобы в степенном ряду выбранный наугад коэффициент был отличен от нуля, то не только бесконечно вероятно, но несомненно, что этот степенной ряд непродолжаем». Очевидно, эта сентенция не имеет ни логических, ни литературных достоинств, но она сослужила мне хорошую службу, сохраняя мой интерес живым.

Идея определенного доказательства пришла мне в голову довольно ясно, но в течение нескольких дней после этого я не пытался разработать окончательную форму доказательства. В продолжение этих дней сеня преследовало слово «пересадка». Действительно, это слово описывало решающую идею доказательства настолько точно, насколько возможно одним словом описать сложную вещь.

Я выдумывал, конечно, различные объяснения для этой «силы слов», но, пожалуй, лучше подождать с объяснениями до тех пор, прока не будет больше примеров[121].

16. Это слишком невероятно, чтобы быть всего лишь совпадением. Пусть f обозначает число простых множителей целого числа n. Назовем n «четно факторизуемым» или «нечетно факторизуемым» в соответствии с тем, является ли f четным или нечтным. Например:

30 =	2 × 3 × 5	— нечетно факторизуемо,
60 =	2 × 2 × 3 × 5	— четно факторизуемо.

Простые числа, 2, 3, 5, 7, 11, 13, 17, … нечетно факторизуемы, квадраты — четно факторизуемы, и число 1 должно рассматриваться как четно факторизуемое, так как оно не имеет простых множителей, а 0 — число четное[110]. Среди двенадцати первых чисел

1	2	3	4	5	6	7	8	9	10	11	12
ч	н	н	ч	н	ч	н	н	ч	ч	н	н

пять четно факторизуемы, а семь — нечетно. Если мы посмотрим на последовательность букв «ч» и «н» в предыдущей таблице, то едва ли сумеем обнаружить простое правило. Эти два вида чисел кажутся чередующимися неправильно, непредсказуемо, случайно. Идея случайности приходит нам в голову почти с неизбежностью: естественно думать, что мы получили бы подобную же последовательность, если бы вместо того, чтобы брать на себя труд разлагать предложенное целое число на множители, просто подбрасывали монету и писали «ч» или «н» в зависимости от того, выпала ли

277

решетка или герб[111]. Естественно также подозревать, что эта монета является «честной», что герб и решетка выпадают приблизительно одинаково часто, что два вида целых чисел — четно и нечетно факторизуемые — одинаково часты.

Так вот, можно доказать (доказательство трудное)¸ что если n велико, среди первых n целых чисел приблизительно столько же четно, сколько и нечетно факторизуемых (когда n стремится к ∞, отношение стремится к 1). Это, по-видимому, подкрепляет наши подозрения. Теперь вы более уверенно ожидали бы, что четно и нечетно факторизуемые числа будут следовать одно за другим как случайная последовательность гербов и решеток. Так именно думая, я начал для каждого n записывать, какого рода числа, нечетно или четно факторизуемые находятся среди первых n чисел. Первые записи выглядели несимметрично, кривобоко. Я удивился и перешел к бо́льшим значениям n: они все еще были кривобокими. Я был поажен и перешел к еще бо́льшим значениям n, но они были все так же кривобоки. Я устал от вычислений, когда достиг n = 1500, и должен был признать, что наблюдения являются доводом в пользу предположения: «Среди первых n целых чисел при n ≥2 четно факторизуемые числа никогда не находятся в большинстве».

Вы подбрасываете монету 1500 раз. Вы подсчитываете, сколько гербов вы получили в первых n испытаниях. Легко может случиться, что вы получите меньше решеток, чем гербов («меньше» понимайте в широком смысле: как «не больше»». Может даже случиться, что, начав со второго шага, для n = 2, 3, 4, …, 1500 вы будете получать все время меньше решеток, чем гербов, но это не может так уж легко случиться. Невольно хочется сказать, что это слишком невероятно, чтобы быть всего лишь совпадением. Тем не менее невероятное действительно случилось и наблюдалось, когда мы играли в орлянку с факторизованными числами. Должна же быть какая-то причина. Я сделал то, что должен был сделать: я принял это предположение без доказательства (конечно, на пробу) и попытался вывести из него следствия. Мне настолько повезло, что я заметил два обстоятельства. Во-первых, если бы новое предположение было справедливо, то из него необходимо следовала бы справедливость значительно более важного предположения, принадлежащего Риману (о ζ-функции). Во-вторых, если бы было справедливо немного больше, чем это новое предполжение (если бы четно факторизуемые числа определенно были в меньшинстве для всех n, начиная с некоторого), то необходимо следовало бы другое предположение, принадлежащее Гауссу (о числе классов квадратичных форм). Оба обстоятельства, мне кажется, говорят в пользу нового предположения.

Это предположение давно уже не является новым, но его судьба все еще не решена. А. Ингам вывел из него следствия, которые, возможно, стремятся сделать его менее правдоподобным. С другой стороны, Д. Лемер путем вычислений убедился, что оно верно для чисел до n = 600 000.

17. Совершенство аналогии. «Из всех тел с данным объемом наименьшую поверхность имеет шар». Это — классическая изопериметрическая теорема в пространстве, замечательный физический аналог которой был открыт А. Пуанкаре и строго доказан Г. Сеге: «Из всех тел с данным объемом наименьшую электрическую емкость имеет шар». Естественно думать, что должны существовать и другие аналогичные теоремы, и я разыскивал теорему такого рода. Силовое поле вокруг тела, заряженного электричеством, сходно с полем скоростной жидкости вокруг тела, движущегося с постоянной скоростью в несжимаемой идеальной жидкости. (Оба поля являются полями без источников и безвихревыми и, следовательно, удовлетворяют одному и тому же дифференциальному уравнению в частных производных.) Емкость тела в электростатическом поел в общих чертах соответствует «присоединенной массе» тела в гидродинамическом поле. (Движущееся тело возмущает жидкость и добавляет к своей собственной кинетической энергии кинетическую энергию движущейся жидкости; «присоединенная масса» есть множитель этой добавочной кинетической энергии.) И емкость, и присоединенная масса связаны с энергией соответствующего поля. Однако имеется бросающееся в глаза различие: емкость зависит только

278

от формы и размеров тела, а присоединенная масса зависит также и от направления движения тела. Чтобы сделать аналогию более совершенной, я должен был ввести новое понятие: осредняя присоединенную массу по всем возможным направлениям, мы получаем среднюю присоединенную массу. И таким образом возникло предположение: «Из всех тел с данным объемом наименьшую среднюю присоединенную массу имеет шар.

Эллипсоид является единственным телом, для которого присоединенная масса в явном виде вычислена во всех направлениях. В самом деле, оказалось, что из всех эллипсоидов с данным объемом наименьшую среднюю присоединенную массу имеет шар: предположение подтвердилось в важном частном случае. Я мог бы подкрепить предположение также и аналогией: мне удалось доказать аналогичное гидродинамическое минимальное свойство круга в случае двух измерений. Так подкрепленное предположение заслуживает быть публично высказанным, по крайней мере я так думаю.

Это предположение до настоящего времени не доказано и не опровергнуто, хотя Г. Сеге и М. Шиффер нашли интересные связанные с ним результаты, которые кажутся подкрепляющими его.

18. Новое предположение. Рассмотрим плоскость с прямоугольными координатами x и y и в этой плоскости — область R, ограниченную замкнутой кривой C. Мы разыскиваем функцию u = u(x, y), удовлетворяющую[112] тому или иному из двух граничных условий:

(1) u = 0,

вдоль кривой C и дифференциальному уравнению в частных производных

внутри области R. (2) n обозначает нормаль к кривой C; в (3) v обозначает некоторую константу. Итак мы имеем две различные задачи: в первой мы должны решить дифференциальное уравнение (3) с краевым условием (1), во второй — с (2). Обе задачи важны в физике в связи с различными явлениями колебаний. Обе задачи имеют одно и то же тривиальное решение: u = 0 тождественно. Как та, так и другая задача имеют нетривиальные, т. е не тождественно равные нулю, решения u только для специальных значениv: задача с граничным условием (1) для v = λ₁, λ₂, λ₃, … , задача с граничным условием (2) для v = μ₁, μ₂, μ₃, … При этом

0 < λ₁ < λ₂ ≤λ₃ ≤λ₄ ≤ …,

0 = μ₁ < μ₂ ≤ μ₃ ≤ μ₄ ≤ …

Эти исключительные значения λ₁, λ₂, λ₃, … и μ₁, μ₂, μ₃, … называются собственными значениями, соответственно, первой и второй задач. Собственные значения связаны с частотами характеристических колебаний в соответствующих физических явлениях.

Я хочу сформулировать новое предположение Пусть A обозначает площадь области R; тогда для n = 1, 2, 3, …

μ_n < 4πnA ^{– 1} < λ_n.

Это — предположение, бросающее вызов. Поскольку форма области R может произвольно меняться и n пробегает все целые числа 1, 2, 3, … , это предположение покрывает необъятное разнообразие частных случаев, из которых известны не слишком многие: предположение могло бы быть опровергнуто числовым результатом, касающимся любого из этих частных случаев. Однако предположение не так уж плохо подкреплено

(a) Предположение подтверждается для n = 1, 2, 3, … , когда R прямоугольник. Это был в действительности тот частный случай, который натолкнул на мысль о предположении.

279

(b) Предположение подтверждается для n = 1, 2, когда R имеет произвольную форму. Этот частный случай очень отличен от случая, упомянутого в (a).

(c) Предположение подтвердилось числовыми выкладками в нескольких частных случаях, в которых собственные значения могут быть вычислены в явном виде: для n до 25 и для специальных форм R (круг, несколько круговых секторов, несколько треугольников).

(d) Было давно известно, что

μ₁ ≤ λ₁, μ₂ ≤ λ₂, μ₃ ≤ λ₃, …

Это находится в согласии с предположением.

(e) Известно также, что

и это также находится в согласии с предположением.

Конечно, никакое количество таких подтверждений не может доказать предположения или заставить кого-либо в какой-то степени в него поверить. Однако такие подтверждения могут повысить интерес к предположению, подтолкнуть нас к испытанию дальнейших следствий и прибавить «изюминку» к научному исследованию, которое является raison d’être[113] предположения.

Технические детали о сформулированном предположении (за часть из которых я чрезвычайно обязан Петеру Сеге[114]) будут опубликованы где-нибудь в другом месте.

19. Еще одно новое предположение. «Если F′(x) — алгебраическая функция и все коэффициенты a₁, a ₂, a ₃, … ряда

F(x) = a₁x + a₂x² + a₃x³ + …

Являются целыми числами, то F(x) — также алгебраическая функция». Иными словами: «Если интеграл от алгебраической функции не является сам алгебраической функцией, то он не может быть представлен степенным рядом с целыми коэффициентами».

Для иллюстрации рассмотрим разложение

Производная от arcsin 2x есть алгебраическая функция, и все коэффициенты разложения этой производной являются целыми, как мы видим из приведенной выше формулы. Поэтому если рассматриваемое предположение верно, то в написанном выше разложении должно быть бесконечно много коэффициентов, не являющихся целыми числами. В этом легко убедиться: если 2n + 1 — простое число, то оно не является делителем числа (2n)1[115]. Итак, исследованный случай подкрепляет предположение, которое подкрепляется также (и было подсказано) следующим фактом: если в предлагаемое предположительное утверждение вместо слов «алгебраическая функция» мы подставим слова «рациональная функция»[116], то мы изменим его в верное и доказанное утверждение. Предположение подкрепляется также довольно смутными аналогиями, «атмосферой», окружающей вопрос о степенны́х рядах с целочисленными коэффициентами; см. пример 14.

Существует много случаев, сходных со случаем arcsin 2x, которые легко могли бы быть проверены, но еще не исследованы. Без тщательного исследования этих доступных следствий такое предположение не следовало бы печатать. Я публикую его здесь как пример неразвитого, недостаточно еще подкрепленного предположения.

20. Что типично? Насколько я могу судить, в последних примерах (примеры 12—19) нет ничего, что не было бы согласно с общим впечатлением,

280

выведенным из предыдущих примеров. В этих последних примерах, как в других, рассматриваемое предположение подкреплено дважды: какими-нибудь ясными фактами и «общей атмосферой». Первый вид подкрепления, подкрепление ясными фактами, как мне кажется, находится в рамках схем, намеченных в этой и в предыдущей главах: аналогия и подтвержденные следствия имеют основное значение, некоторую роль играют также просто правдоподобные следствия; подкрепление с двух весьма различных сторон воспринимается как жизнеспособное. В целом примеры 12—19 представляются типичными.

Ни одно из упомянутых в примерах 13—17 предположений не опровергнуто (по крайней мере на сегодня). Это могло бы показаться нетипичным. Я не упоминал здесь, однако, бесчисленное множество других моих предположений, которые были опровергнуты через несколько минут или часов или дней; такие недолговечные предположения очень быстро забываются[117]. Конечно, я опубликовал только предположения, прошедшие все очевидные испытания, которые я смог придумать, и выдержавшие работу над ними по крайней мере в течение нескольких месяцев; это — наиболее стойкие предположения, имеющие наилучшие шансы выжить. В типичном случае исследование состоит в создании многих предположений, опровержении большей части из них и сохранении нескольких.

XIV. СЛУЧАЙ. НЕИЗМЕННОЕ СОПЕРНИЧАЮЩЕЕ ПРЕДПОЛОЖЕНИЕ

…вероятность того, что это совпадение является только делом случай, поэтому значительно меньше, чем (1/2)⁶⁰… Следовательно, это совпадение должно быть произведено какой-то причиной, и может быть определена причина, дающая совершенное объяснение полученных из наблюдения фактов. — Г. Кирхгоф[122]

1. Случайные массовые явления. В обычной речи слова «вероятно», «очень возможно», правдоподобно» употребляются в значениях, которые четко не различаются. Теперь мы выберем слово «вероятно» и научимся употреблять это слово в специфическом значении, как технический термин ветви науки, называемой «Теорией вероятностей»[123][118].

Эта теория имеет огромное разнообразие приложений и аспектов, и поэтому ее можно представлять себе и вводить различными путями[119]. Некоторый авторы рассматривают ее как чисто математическую теорию, другие — как вид или ветвь логики, а еще одни — как часть науки о природе. Эти различные точки зрения могут быть, но могут и не быть несовместимыми. Мы должны начать с изучения одной из них, но нам не следовало бы связывать себя любой из них. В следующей главе мы несколько изменим свою позицию, но в настоящей главе мы выбираем точку зрения, которая наиболее удобна в огромном большинстве приложений и которой начинающий может овладеть наиболее быстро. Мы рассматриваем здесь теорию вероятностей как часть науки о природе, как теорию некоторых доступных наблюдению явлений, случайных массовых явлений[124]. Что означает этот термин, мы можем понять довольноясно, если сравним несколько знакомых примеров таких явлений.

(1) Дождь. Дождь — массовое явление. Оно состоит из очень большого числа отдельных событий, из падения очень большого числа дождевых капель. Эти капли, хотя и очень похожие одна на другую,

282

отличаются в различных отношениях: в размере, в месте, где они падают на землю и т. д.[120] В поведении дождевых капель есть нечто такое, что мы должным образом описываем словом «случайное». Чтобы ясно понять значение этого термина, представим себе такой эксперимент.

Понаблюдаем первые капли на мостовой, когда начал идти дождь. Мы наблюдаем мостовую в середине какого-нибудь большого городского сада, достаточно далеко от строений или деревьев или чего-нибудь, что могло бы помешать дождю. Сосредоточим свое внимание на двух камнях, которые мы назовем «правым камнем» и «левым камнем». Мы наблюдаем капли, падающие на эти камни, и отмечаем порядок, в котором они ударяются. Первая капля упала на левый камень, вторая — на правый, третья — снова на правй, четвертая — на левый и т. д. без видимой закономерности, например:

Л П П Л Л Л П Л П Л П П Л П П

(П для правого, Л для левого). В этой последовательности дождевых капель нет никакой закономерности. Действительно, понаблюдав некоторое число капель, мы не можем разумно предсказать, куда упадет следующая капля. Мы сделали выше пятнадцать записей. Глядя на них, можем ли мы предсказать, какой будет шестнадцатая запись, П или Л? Очевидно, не можем. С другой стороны, в падении дождевых капель какого-то рода закономерность существует. В самом деле, мы можем уверенно предсказать, что в конце дождя оба наши камня будут одинаково мокры, т. е. число капель, упавших на каждый камень, будет почти пропорционально площади его открытой горизонтальной поверхности. В том, что эт так, никто не усомнится, метеорологи, конечно, предполагают, что это так, при конструировании своих дождеметров[121]. Все же здесь есть что-то парадоксальное. Мы можем предвидеть, что произойдет в конечном итоге, но не можем предвидеть деталей. Дождь — типичное случайное массовое явление, непредсказуемое в некоторых деталях, предсказуемое в некоторых числовых пропорциях целого[122].

(2) Мальчики среди новорожденных. В родильном доме новорожденные дети регистрируются в том порядке, в котором они рождаются. Мальчики и девочки (М и Д) следуют друг за другом без видимой закономерности, например:

Д М М Д М Д М М Д Д М М М Д Д

Хотя мы не можем предсказать деталей этой случайной последовательности, мы вполне можем предсказать важное свойство окончательного результата, получаемого суммированием всех таких регистраций в Соединенных Штатах на протяжении года: число мальчиков будет больше, чем число девочек; в действительности отношение этих двух чисел будет мало отличаться от отношения 51,5 : 48,5. Число рождений в Соединенных Штатах составляет приблизительно

283

3 миллиона в год. Мы имеем здесь случайное массовое явление значительного объема[123].

(3) Азартная игра. Мы многократно подбрасываем монету, каждый раз отмечая, какая сторона выпала: «решетка» или «герб» (Р или Г). Так мы получаем последовательность без видимой закономерности, например:

Г Р Р Р Г Р Г Р Р Г Р Г Р Г Г

Если у нас хватит терпения подбросить монету несколько сот раз[124], то выяснится определенное отношение гербов к решеткам, которое значительно не изменится, если мы продолжим наш эксперимент еще дальше. Если наша монета «честная», то в конечном итоге должно было бы появиться отношение 50 : 50. Если монета «нечестная», то обнаружится какое-нибудь другое отношение. Как бы то ни было, мы снова видим характерную особенность случайного массового явления. Хотя детали и непредсказуемы, в конце концов появляется постоянное отношение. Несмотря на иррегулярность индивидуальных событий, имеется общая закономерность.

2. Понятие вероятности. В 1943 г. числа рождений мальчиков, и общее число рождений в Соединенных Штатах, соответствено, были:

1 506 959, 1 427 901, 2 934 860.

Мы называем

1 506 959 частотой рождения мальчиков,

1 427 901 — частотой рождения девочек.

Мы называем

относительной частотой рождения мальчиков и

относительной частотой рождения девочек. Вообще, если событие некоторого рода произошло в m случаях из n, то m мы назыаем частотой появления события этого рода, а m/n его относительной частотой.

Представим себе, что в течение всего года по всем Соединенным Штатам последовательно регистрируются рождения (как в родильном доме, о котором мы упоминали в предыдущем параграфе)[125]. Если мы посмотрим на последовательность рождений мальчиков и девочек, то будем перед собой иметь длинную серию, состоящую из почти трех миллионов записей, начинающуюся примерно так:

Д М М Д М Д М М Д Д М М М Д Д

284

Когда развертывается это массовое явление, мы имеем на каждой стадии наблюдения некоторую частоту рождения мальчиков, а также некоторую относительную частоту. Отметим после 1, 2, 3, … наблюдений частоты и относительные частоты, найденные до этого момента:

Наблюдения	Событие	Частота М	Относительная частота
1	Д	0	0/1 = 0,000
2	М	1	1/2 = 0,500
3	М	2	2/3 = 0,677
4	Д	2	2/4 = 0,500
5	М	3	3/5 = 0,600
6	Д	3	3/6 = 0,500
7	М	4	4/7 = 0,571
8	М	5	5/8 = 0,625
9	Д	5	5/9 = 0,556
10	Д	5	5/10 = 0,500
11	М	6	6/11 = 0,545
12	М	7	7/12 = 0,583
13	М	8	8/13 = 0,615
14	Д	8	8/14 = 0,574
15	Д	8	8/15 = 0,533

В пределах нашей таблицы относительная частота довольно сильно колеблется (между границами 0,000 и 0,677). Однако мы здесь имеем лишь очень небольшое число наблюдений. Когда мы будем идти все дальше и дальше, колебания относительной частоты будет становиться все менее и менее сильными и мы можем с уверенностью ожидать, что в самом конце она будет очень мало колебаться около своего окончательного значения 0,5135. Когда число наблюдений увеличивается, относительная частота несмотря на все непредсказуемые иррегулярности[126] деталей по-видимому устанавливается на устойчивом окончательном значении[127]. Такое поведение, появление в конце концов устойчивой относительной частоты, типично[128] для случайных массовых явлений.

Важной целью любой теории таких явлений должно быть предсказание окончательной устойчивой относительной частоты или относительной частоты дальнего действия. Мы должны рассмотреть теоретическое значение относительной частоты дальнего действия и мы будем называть это теоретическое значение вероятностью.

Постараемся пояснить это понятие вероятности. Естественно, мы начнем с изучения тех массовых явлений, для которых мы можем предсказать относительную частоту дальнего действия с некоторой степенью разумной уверенности.

(1) Шары в мешке. Мешок содержит p шаров различного цвета, среди которых имеется точно f белых шаров. Воспользуемся этим простым устройством[129], чтобы вызвать случайное массовое явление. Мы вытаскиваем шар, замечаем его цвет и пишем Б, если шар белый,

285

и Д, если он другого цвета. Только что вытащенный шар мы кладем обратно в мешок[130], перемешиваем шары в мешке, затем снова вытаскиваем шар и отмечаем цвет этого второго шара, Б или Д[131]. При этом мы получаем случайную последовательность, похожую на последовательности, рассмотренные в § 1:

Б Д Д Д Б Д Д Б Б Д Д Д Б Б Д

Какова относительная частота дальнего действия белых шаров?

Обсудим обстоятельства, при которых с разумной уверенностью мы можем предсказать искомую частоту. Допустим, что шары однородны и точно сферические, сделаны из одного и того же материала и имеют один и тот же радиус. Их проерхности одинаково гладкие, и их различная окраска, если вообще и оказывает какое-нибудь влияние на их механические свойства, то лишь совершенно незначительное. У человек, вытаскивающего шары, завязаны глаза или какая-либо другая причина не позволяет ему видеть шары. Положение шаров в мешке от одного вытаскивания до другого меняется, является непредсказуемым, находится вне нашего контроля. Однако неизменные обстоятельства вполне находятся под контролем: все шары имеют одинаковую форму, размеры и вес: они неразличимы человеком, который их вытаскивает.

При таких обстоятельствах мы не видим никаких причин, почему один шар следовало бы предпочесть другому, и естественно ожидаем, что в конечном счете каждый шар будет вытащен приблизительно одинаково часто. Скажем, у нас хватит терпения произвести 10 000 вытаскиваний тогда мы должны были бы ожидать, что каждый из p шаров появится около

Имеется f белых шаров. Следовательно, за 10 000 вытаскиваний мы ожидаем достать белый шар

Это ожидаемая частота появления белых шаров. Чтобы получить относительную частоту, мы должны разделить частоту на число наблюдений или вытаскиваний, т. е. на 10 000. и, таким образом, мы пришли к утверждению: относительная частота дальнего действия, или вероятность появления белых шаров равна f/p.

Буквы f и p выбраны в согласии с традиционными обозначениями. Когда мы должны вытащить один из p шаров, мы должны выбрать один из p возможных (possible) случаев. Мы имеем достаточно оснований (равные условия для всех p шаров) не предпочитать любой из этих p возможных случаев другому. Если бы мы желали, чтобы был вытащен белый шар (например, если бы мы держали пари о белом шаре), то f белых шаров казались бы нам благоприятствующими

286

(favorable) случаями. Следовательно, мы можем описать вероятность f/p как отношение числа благоприятствующих случаев к числу возможных случаев.

Вытаскивать шар из мешка, класть его обратно в мешок, встряхивать мешок, вытаскивать другой шар и повторять это n раз — по-видимому, довольно глупое занятие. Не теряем ли мы свое время попусту, обучаясь такой примитивной игре? Я так не думаю. Мешок и шары, с которыми мы поступаем описанным способом, порождают случайное массовое явление, особенно простое и доступное. Обобщение, естественно, начинается с наиболее простого, наиболее прозрачного частного случая. Наука динамика родилась, когда Галилей начал изучать падение тяжелых тел. Наука о вероятности родилась, когда Ферма и Паскаль начали изучать азартные игры, в которых приходится бросать кости или вытягивать карты из колоды или вытаскивать шары из мешка[125]. Основные понятия и законы динамики могут бытьизвлечены из простого явления падения тел. Мы пользуемся мешком и шарами, чтобы понять основное понятие вероятности.

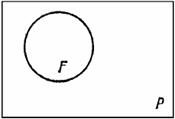
Рис. 14.1. Вероятность, определенная дождем.

(2) Дождь. Возвратимся к рассмотрению случайного массового явления, с которого мы начали в § 1. Площадь горизонтальной поверхности равна P, а площадь некоторой части этой поверхности равна F; см. рис. 14.1. Мы наблюдаем дождевые капли, падающие на площадь П, и интересуемся частотой падения дождевых капель на меньшую площадь F. Мы склонны без колебаний предсказать относительную частоту дальнего действия: доля всего дождя (падающего на всю площадь), приходящаяся на меньшую площадь, если дождь состоит более чем из нескольких капель будет очень близка к F/P. Иными словами, вероятность того, что дождевая капля, падающая на поверхность площади P, упадет на участок площади F, равна F/P. Если мы идеализируем дождь и рассмотрим дождевую каплю как геометрическую точку, то сможем также сказать: вероятность того, что точка, падающая на площадь P, упадет на частичную площадь F, равна F/P.

В последнем утверждении мы рассматриваем каждую точку площади P как возможный слуай, а каждую точку частичной площади F — как благоприятствующий случай. Число благоприятствующих

287

случаев, как и число возможных случаев, бесконечно, и не имело бы смысла[132] говорить об отношении бесконечных чисел. Мы можем, однако, рассматривать площадь поверхности как меру множества точек, содержащихся в этой поверхности. Пользуясь этим термином, мы можем описать вероятность F/P как отношение меры множества благоприятствующих случаев к мере множества возможных случаев.

3. Применение мешка и шаров. При выводе фундаментального принципа статики Лагранж заменил произвольную систему подходящей системой блоков. В свете этого рассуждения Лагранжа (детали которого здесь не нужны) любой случай равновесия проявляется как подходящая комбинация правильно подобранных блоков[126]. Исчисление вероятностей можно рассматривать подобным же образом; фактически такой взгляд подсказывается ранней историей этой науки. С этой точки зрения любую задачу о вероятности, по-видимому, можно сравнить с подходящей задачей о мешках, содержащих шары, и любое случайное массовое явление проявляется как сходное в некоторых существенных отношениях с последовательными вытаскиваниями шаров из системы подходящим образом скомбинированных мешков. Проиллюстрируем это несколькими простыми примерами.

(1) Вместо подбрасывания честной монеты, мы можем вытаскивать шар из мешка, содержащего ровно два шара, один из которых помечен буквой Г, а другой — Р (гербы и решетки). Вместо бросания правильной игральной кости мы можем вытаскивать шар из мешка, содержащего ровно шесть шаров, помеченных, соответственно, 1, 2, 3, 4, 5 и 6 очками. Вместо вытягивания карты из колоды карт мы можем вытаскивать шар из мешка, содержащего 52 соответствующим образом помеченных шара. Интуитивно кажется ясным, что подходящим образом заменяя монеты, кости, карты и другие подобные приспособления мешком с шарами, мы не изменим условий в обычных азартных играх. По крайней мере мы не изменим шансов в тех идеализированных вариантах этих игр, в которых применяемые приспособления (монеты, кости и т. д.) предполагаются совершенно симметричными и некоторые основные шансы соответственно совершенно равными.

(2) Желая изучить случайность в распределении мальчиков и девочек среди новорожденных, мы можем заменить действительное массовое явление последовательными вытаскиваниями шаров из мешка, содержащего 1000 шаров, 515 из которых помечены буквой М и 485 буквой Д. Эта замена является, конечно, теоретической, поскольку каждая теория ограничена, условной и приближенной. Однако гла вное состоит в том, что мешок и шары дают нам возможность сформулировать теорию.

288

(3) Метеоролог регистрирует последовательность дождливых и недождливых дней в какой-то местности. Его наблюдения, по-видимому, показывают, что в целом каждый день стремится походить на предыдущий: за недождливыми днями как будто охотнее, чем дождливые, следуют недождлдивые же дни и, подобным же образом, за дождливыми днями как будто охотнее, чем недождливые, следуют дождливые дни. Конечно, заслуживающая доверия закономерность проявляется только в длинном ряде наблюдений; детали иррегулярны, кажутся случайными[133].

Метеоролог может пожелать более ясно выразить свои впечатления, которые мы только что бегло набросали. Если он хочет сформулировать теорию на языке вероятности, то он может рассмотреть три мешка. Каждый мешок содержит одно и то же число шаров, скажем 1000. Некоторые из шаров белые, другие черные (белые для недождливых дней, черные для дождливых[134]). Однако между мешками имеется важное различие. Каждый мешок имеет надпись, видную человеку, вытаскивающему шары. На одном мешке написано «НАЧАЛО», на другом — «ПОСЛЕ БЕЛОГО», на третьем — «ПОСЛЕ ЧЕРНОГО». Отношение числа шаров разного цвета в различных мешках различно. В каждом мешке отношение числа белых шаров к числу черных приближает наблюдаемое отноешние числа недождливых дней к числу дождливых в различных обстоятельствах. В мешке «НАЧАЛО» отношение равно отношению числа недождливых дней к числу дождливых за весь год, в мешке «ПОСЛЕ БЕЛОГО» это отношение равно отношению числа недождливых дней к числу дождливых дней, следующих за недождливым днем, а в мешке «ПОСЛЕ ЧЕРНОГО» это отношение равно отношению числа недождливых дней к числу дождливых, следующих за дождливым днем. Таким образом, мешок «ПОСЛЕ БЕЛОГО» содержит больше белых шаров, чем мешок «ПОСЛЕ ЧЕРНОГО». Шары вытаскиваются один за другим, и каждый вытащенный шар, когда его цвет отмечен, возвращается в мешок, из которого он был взят. Мешок «НАЧАЛО» используется только один раз для первого шара. Если первый шар белый, то для второго шара мы пользуемся мешком «ПОСЛЕ БЕЛОГО», но если первый шар черный, то второй шар вытаскивается из мешка «ПОСЛЕ ЧЕРНОГО». И так далее, цвет только что вытащенного шара определяет мешок из которого должен быть вытащен следующий шар.

Это только теория, что последовательность белых и черных вытащенных шаров при описанных обстоятельствах с разумным приближением воспроизводит последовательность недождливых и дождливых дней. Однако на первый взгляд эта теория не кажется неуместной. Как бы то ни было, эта теория или какая-нибудь подобная теория могла бы заслуживать того, чтобы ее сопоставили с наблюдениями.

(4) Возьмите любой английский текст (если угодно, из Шекспира) и замените каждую из букв a, e, i, o, u и y на Г, а каждую из остальных двадцати букв — на C. (Г означает гласная, а С — согласная).

289

Вы получите схему вроде

С Г С Г Г С С Г С С Г С Г С С

Эта иррегулярная последовательность в некотором отношении противоположна последовательности, рассмотренной в предыдущем пункте (3): каждый день стремится быть похожим на предыдущий день, но каждая буква стремится быть непохожей на предыдущую букву. Тем не менее мы можем воспроизвести последовательность гласных и согласных букв последовательностью белых и черных шаров, вытаскиваемых из трех мешков, что и раньше [в пункте (3)], однако отношение числа белых шаров к числу черных должно быть не таким, как раньше. Чтобы в согласии с действительностью воспроизвести последовательность гласных и согласных букв, мешок «ПОСЛЕ БЕЛОГО» должен содержать меньше белых шаров, чем мешок «ПОСЛЕ ЧЕРНОГО».

(5) Имеется два мешка. Первый мешок содержит p шаров, среди которых f белых. Второй мешок содержит P фишек, среди которых F белых. Пользуясь обеими руками, я вытаскиваю из обоих мешков одновременно шар левой, а фишку правой рукой. Какова вероятность, что шар и фишка окажутся белыми?

Мы могли бы, конечно, повторить этот простой эксперимент достаточно много, например, тысячу, раз и таким образом[135] получить поиближенное значение для искомой вероятности. Но мы можем также попытаться догадаться, какова эта вероятность, и это более интересно.

Результат двух одновременных вытаскиваний есть «пара», состоящая из шара и фишки. Имеется p шаров и P фишек. Так как каждый шар может быть соединен с любой фишкой, то имеется pP возможных пар; они показаны на рис 14.2, где p = 5, f =2, P = 4, F =3. Нет никаких оснований предпочесть любой из p шаров любому другому шару или любую из P фишек любой другой фишке. По-видимому, нет никаких оснований предпочесть любую из pP пар любой другой паре. В самом деле, когда я произвожу эксперимент с двумя мешками, предполагается, что я действую слепо, наугад, так что каждая рука вытаскивает независимо от другой. «Пусть твоя левая не знает, что делает твоя правая рука». Кажется неправдоподобным, чтобы шансы шара, который я вытаскиваю левой рукой, должны были зависеть от фишки, которую я вытаскиваю правой рукой. Почему шар номер 1 должен быть более привлекательным для фишки номер 1, чем для фишки номер два?[136]

И, таким образом, мы можем вообразить мешок, содержащий pP механически неразличимых предметов (каждый предмет есть пара, шар, соединенный с фишкой); одно вытаскивание из этого единственного мешка равносильно двум одновременным вытаскиваниям из двух мешков, описанных вначале. Мы имеем, таким образом, pP возможных случаев; остается найти число благоприятствующих случаев. Взгляд

290

на рис. 14.2 показывает, что имеется fF пар, состоящих из белого шара и белой фишки. Таким образом мы получаем значение искомой вероятности: она равна

произведению двух вероятностей. В самом деле, f/p есть вероятность вытаскивания белого шара из первого мешка, а F/P есть вероятность вытаскивания белого шара из второго мешка,

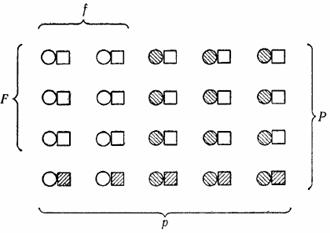
Рис. 14.2. Независимые события.

Для шара и фишки существенно то, что вытаскивание одного из этих предметов не оказывает влияния на шансы вытащить другой. В обычной терминологии исчисления вероятностей такие события называются независимыми одно от другого[137]; совместное наступление обоих событий рассматривается как составное событие. Предыдущее рассмотрение обосновывает правило: Вероятность составного события равна произведению вероятностей составляющих событий, если только эти составляющие события взаимно независимы.

4. Исчисление вероятностей. Статистические гипотезы. Теория вероятностей как мы ее понимаем есть часть науки о природе, теория случайных массовых явлений.

Наиболее поразительным достижением физических наук является предсказание. Астрономы предсказывают солнечные и лунные затмения, положение планет и возвращение комет, которые на несколько лет ускользают от наблюдений. Великому астроному (Леверье) удалось даже предсказать положение планеты (Нептун), самое существование которой ранее было неизвестно. Теория вероятностей с известным[138] успехом предсказывает частоты в некоторых массовых явлениях.

Астрономы основывают свои предсказания на прежних наблюдениях[139], на законах механики, законе тяготения и на длинных трудных вычислениях. Любая из физических наук основывает свои предсказания на какой-то теории или, можно сказать, на каком-то предположении, так как никакая теория не является несомненной[127][140], и, таким образом, каждая теория есть более или менее разумное, более или менее хорошо подкрепленное предположение. Пытаясь предсказать частоты в некотором случайном массовом явлении исходя из теории вероятностей, мы должны сделать какое-то теоретическое допущение относительно этого явления. Такое допущение, которое должно быть выражено на языке вероятности, называется статистической гипотезой.

Когда мы применяем[141] теорию вероятностей, мы должны вычислять вероятности (являющиеся теоретическими приближенными значениями относительных частот). Когда мы пытаемся найти вероятность, мы должны решить задачу. Неизвестным в этой задаче является искомая вероятность. Однако чтобы определить это неизвестное нам нужны данные и условия нашей задачи. Данные обычно являются вероятностями, а условия, от которых зависит связь неизвестной вероятности с данными вероятностями, устанавливает статистическая гипотеза.

Поскольку в приложениях теории вероятностей преобладающую роль играет вычисление вероятностей, эта теория обычно называется исчислением вероятностей. Таким образом, целью исчисления вероятностей является вычисление новых вероятностей на основании данных вероятностей и данных статистических гипотез[142].

Читатель, желающий внимательно прочитать остающуюся часть этой главы, должен быть знаком с элементами исчисления вероятностей, или же ему придется принять некоторые результаты, выведенные из этих элементов, без доказательств. По большей части в тексте эти результаты будут высказываться без вывода; выводы будут даны позже, в первой части Примеров и Примечаний, следующих за этой главой, и в соответствующих решениях. Однако даже если читатель не проверит вывода этих результатов, ему следует несколько вникнуть в лежащие в основании теоретические допущения. Мы можем сделать такие допущения интуитивно понятными: мы сравниваем случайное массовое явление, которое мы исследуем, с вытаскиваниями из подходящим образом наполненных мешков при подходящих условиях, как в предыдущем § 3.

Приложения исчисления вероятностей бесконечно разнообразны[143]. В следующих параграфах этой главы сделана попытка проиллюстрировать главные типы приложений подходящими элементарными

292

примерами. Ударение будет сделано на мотивировке этих приложений, т. е. на таких предварительных рассмотрениях, которые делают выбор приема правдоподобным.

5. Непосредственное предсказание частот. В самом начале своей истории исчисление вероятностей было, в сущности, теорией некоторых азартных игр[128]. Тем не менее предсказания этой теории, вплоть до недавнего времени, в большом масштабе экспериментально не проверялись. Мы начнем с обсуждения одного такого опыта.

(1) В. Ф. Р. Уэлдон Бросил 12 игральных костей 26 306 раз, каждый раз отмечая, на скольких из этих 12 костей выпало больше, чем четыре очка[129]. Результаты этих наблюдений записаны в столбце (4) табл. I; столбец (1) показывает число костей, среди этих 12, на которых выпало пять или шесть очков. Таким образом, в 26306 испытаниях ни одного раза не случилось, чтобы на всех двенадцати костях выпало более чем четыре очка. Наиболее частым был случай, когда пять или шесть очков выпадало на четырех из двенадцати костей; это произошло 6114 раз.

Число пятерок или шестерок (1)	Избыток I (2)	Предсказан. частота I (3)	Наблюдавшаяся частота (4)	Предсказан. частота I (5)	Избыток II (6)
0	+ 18	203	185	187	+ 2
1	+ 67	1215	1149	1146	— 3
2	+ 80	3345	3265	3215	— 50
3	+ 101	5576	5475	5465	— 10
4	+ 159	6273	6114	6269	+ 155
5	+ 176	5018	5194	5115	— 79
6	— 140	2927	3067	3043	— 24
7	— 76	1255	1331	1330	— 1
8	— 11	392	403	424	+ 21
9	— 18	87	105	96	— 9
10	— 1	13	14	15	+ 1
11	— 3	1	4	1	— 3
12	0	0	0	0	0
Всего	0	26 306	26 306	26 306	0

Как может теория предсказать полученные из наблюдений числа, записанные в столбце (4) табл 1? Если мы допустим, что кости являются «честными» и что испытания с различными костями или же с одной и той же костью, произведенные в разное время, независимы одно от другого, то мы сможем вычислить нужные вероятности[144]. При нашем допущении (которе правлиьно называть «статистической

293

гипотезой» вероятность того, что точно на 4 костях из 12 должно выпасть 5 или 6 очков, равна

По определению вероятность есть теоретическое значение относительной частоты дальнего действия. Если событие с вероятностью P наступает в n испытаниях m раз, то мы ожидаем, что

или

m = P_n приближенно.

Поэтому нам следовало ожидать, что точно на 4 костях из 12 пять или шесть очков выпадает приблизительно в

случаях из n = 26306 испытаний. (Заметьте, что мы можем вычислить это число 6273 до того как начались испытания.) И вот, это предсказанное значение 6273 не кажется «очень отличающимся» от полученного из наблюдений числа 6 114, и, таким образом, наше первое впечатление о практической применимости теории вероятностей может быть совсем хорошим[145].

Число 6273 записано в столбце (3) на должном месте, в той же строке, что и число 4 в столбце (1). Подобным же образом получены все числа в столбце (3). Для того чтобы более удобно сравнить предсказанные значения в столбце (3) с полученными из наблюдений числами в столбце (4), мы записали разности (предсказанное минус наблюденное) в столбце (2). Помня о значении столбцов (2), (3) и (4), просмотрим эти столбцы. Является ли согласие между опытом и теорией удовлетворительным? Достаточно ли близки полученные из наблюдений числа к предсказанным значениям?

Очевидно, некоторое согласие между столбцами (3) и (4) существует. Оба столбца чисел имеют один и тот же общий вид: максимум достигается в одном и том же месте (в той же строке) и числа сперва возрастают до максимума, а затем монотонно убывают до 0 — во многих отношениях весьма сходно в обоих столбцах. Отклонения чисел, полученных из наблюдений, от предсказанных значений в большинстве случаев кажутся сравнительно малыми; согласие на первый взгляд кажется совсем хорошим. С другой стороны, однако, число испытаний 26306 представляется довольно большим. Можем ли мы считать отклонения достаточно малыми, учитывая это большое число испытаний?

Это как будто правильный вопрос. Однако мы не можем на него ответить экспромтом; лучше его отложить до тех пор, пока мы не

294

узнаем немножко больше; см § 7 (3). Тем не менее без каких-либо специальных знаний, имея только немного здравого смысла, мы можем вывести из табл. I вполне определенное заключении. В отношении столбцов (3) и (4) физик легко заметил бы следующее. Разности записаны в столбце (2). Некоторые из этих разностей положительны, другие отрицательны. Если бы эти разности были распределены случайно, то знаки + и — должны были бы чередоваться каким-нибудь беспорядочным образом. В действительности, однако, знаки + и — резко отделены: теоретические значения до некоторого места слишком велики, а затем, начиная с этого места, слишком малы. В подобном случае физик говорит о систематическом отклонении теории от эксперимента и такое систематическое отклонение он рассматривает как серьезное возражение против теории.

Итак, согласие между теорией вероятностей и наблюдениями Уэлдона, которое сначала казалось совсем хорошим, начинает выглядеть значительно хуже.

(2) Но за счет чего получилось это систематическое отклонение? Теоретические значения вычислены в соответствии с правилами исчисления вероятностей на основании некоторого допущения, «статистической гипотезы». Нам не следует порицать правил этого исчисления; дефект может заключаться в статистической гипотезе. Действительно, эта статистическая гипотеза имеет слабое место: мы допустили, что кости, которыми пользовались при эксперименте, были «честными». Когда джентльмен играет в кости, он должен допустить, что кости «честные», но для натуралиста такое допущение не оправдано[146].

В самом деле, посмотрим на пример физика. Галилей открыл закон падения тел, который мы сегодня, в обычных обозначениях, записываем как уравнение

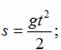
s обозначает путь (расстояние), t — время. точнее, Галилей форму зависимости s от t: расстояние пропорционально квадрату времени t. Однако он не сделал никакого теоретического предсказания относительно постоянной g, входящей в эту пропорциональность; подходящее значение g должно быть найдено с помощью экспериментов. В этом отношении, как и во многих других отношениях, естествознание следует примеру Галилея; в бесчисленном множестве случаев теория дает общую форму какого-нибудь закона природы, а эксперимент должен определить числовые значения постоянных, входящих в математическое выражение закона. Этот прием годится и в нашем примере.

Если кость «честная»[147], то ни одну из шести граней нельзя предпочесть другой и, таким образом, вероятность выпадения 5 или 6 очков равна

295

Даже в том случае, если кость не является честной, существует определенная вероятность p выпадения 5 или 6 очков; p может отличаться от ⅓. (Однако для обыкновенной кости не очень сильно; в противном случае мы рассматривали бы ее как «налитую свинцом»[148]) Рассмотрим p как константу, которую следует определить с помощью экспериментов. И теперь мы видоизменим нашу первоначальную статистическую гипотезу; мы допустим, что все двенадцать костей, которыми пользовался Уэлдон, имеют одну и ту же возможность p выпадения 5 или 6 очков. (Это простое допущение, но, конечно, довольно произвольное. Мы не можем верить, что оно в точности соответствует истине; мы можем только надеяться, что оно не очень далеко от истины. В сущности, не бывает случая, чтобы кости были в точности одинаковы, но они могут только слегка отличаться.) Мы сохраним неизменной другую часть прежней статистической гипотезы (различные кости и различные испытания рассматриваются как независимые).

На основании этой статистической гипотезы мы снова можем указать теоретические значения, соответствующее наблюдениям, записанным в столбце (4) табл. I. Например, теоретическое значение, соответствующее полученному из наблюдений значению 6114, равно

495p⁴(1— p)⁸26 306;

оно зависит от p так же, как и теоретические значения¸ соответствующие другим числам в столбце (¸ соответствующие другим числам в столбце (4), зависят от p.

Остается определить p из экспериментов, которые мы исследуем. Мы не можем надеяться определить вероятность p из экспериментов точно, а можем надеяться определить ее только с некоторым разумным приближением. Если мы изменим на минуту свою точку зрения и рассмотрим в качестве испытания бросание единственной кости, то следует считать, что было выполнено

12 × 26 306 = 315 672

испытаний; это очень большое число. Частота события пить или шесть очков может легко быть выведена из столбца (4) табл. I. Мы находим в качестве значения относительной частоты

эту относительную частоту, получившуюся в результате очень большого числа испытаний¸ мы принимаем за значение p. ) Мы допустили, таким образом, для p значение чуть большее, чем ⅓.)

Раз p выбрано, мы можем вычислить теоретические значения, соответствующие полученным из наблюдения частотам. Эти теоретические значения записаны в столбце (5) табл. I. Таким образом, столбцы (3) и (5) дают теоретические значения, соотвествующие одним и тем же полученным из наблюдения числам, но вычисленные

296

при различных статистических гипотезах. В действительности эти две статистических[149] гипотезы[150] отличаются только значением p; в столбце (3) мы пользуемся p = ⅓, в столбце (5) — чуть-чуть бо́льшим значением, выведенным из наблюдений. (числа из столбца (3) могут быть вычислены до наблюдений, но числа из столбца (5) до наблюдений вычислить нельзя.) Разности между соответствующими числами столбцов (5) и (4) записаны в столбце (6).

Вряд ли приходится сомневаться в том, что теоретические значения в столбце (5) значительно лучше соответствуют наблюдениям, чем значения в столбце (3). По абсолютной величине разности в столбце (6) за одним лишь исключением меньше или равны разностям в столбце (2) (равны ровно в трех случаях, значительно меньше в бо́льшей части случаев). В противоположность столбцу (2), знаки + и — в столбце (6) чередуются, так что они не дают никаких оснований ожидать систематического отклонения теоретических значений в столбце (5) от экспериментальных данных в столбце (4).

Как сообщается аккуратной официальной Швейцарской статистической службой, за тридцать лет, с 1871 по 1900 г. в Швейцарии было точно 300 случаев рождения тройни (т. е. родилось 900 детей. Говоря о рождениях, мы считаем матерей, а не младенцев.) Число всех рождений (несколько рождений тройни, несколько — двойни и большая часть, конечно, рождений одного ребенка) за тот же период в той же стране равнялся 2 6123 246. итак, мы имеем здесь массовое явление значительного объема, но рассматриваемое событие, рождение тройни, является редким событием. Среднее число рождений за год равно

2 6123 246/30 = 87 075,

среднее же число рождений тройни равно только

300/30 = 10.

Конечно, это событие в одни годы наступало чаще, в другие реже, чем, в среднем, 10 раз, а в некоторые годы — точно 10 раз. Табл II в столбце (2) дает соответствующие подробности. Мы видим там (в строке, в которой в первом столбце стоит 10), что в рассматриваемый период было точно 4 года, когда имели место ровно 10 рождений тройни. Как показывает тот же столбец (2), за этот период ни в один год не было меньше, чем 3 таких рождений[151], ни в один год не было больше, чем 17 и каждое из этих крайних чисел достигалось только в один год.

297

Таблица II

Тройни, родившиеся в Швейцарии в 1871—1900 гг.

Рождения (1)	Наблюдавшиеся годы (2)	Теоретические годы (3)	(2) накопл. (4)	(3) накопл. (5)
0	0	0,00	0	0,00
1	0	0,00	0	0,00
2	0	0,09	0	0,09
3	1	0,21	1	0,30
4	0	0,57	1	0,87
5	1	1,14	2	2,01
6	1	1,89	3	3,90
7	5	2,70	8	6,60
8	1	3,39	9	9,99
9	4	3,75	13	13,74
10	4	3,75	17	17,49
11	4	3,42	21	20,91
12	3	2,85	24	23,76
13	2	2,16	26	25,92
14	1	1,59	27	27,51
15	2	1,02	29	28,53
16	0	0,66	29	29,19
17	1	0,39	30	29,58
18	0	0,21	30	29,799
19	0	0,12	30	29,91

Числа в столбце (2) кажутся разбросанными каким-то случайным образом. Интересно отметить, что исчисление вероятностей в состоянии сопоставить неправильно выглядящие полученный из наблюдений числа в столбце (2) с теоретическими числами, следующими простому закону; см. столбец (3). Согласие столбцов (2) и (3), если судить по беглому взгляду, не кажется плохим; разность между двумя числами — полученным из наблюдений и теоретическим — во всех случаях, за исключением двух, по абсолютной величине меньше, чем 1. Однако в этих двух случаях (строки с 7 и 8 в первом столбце) разность по абсолютной величине больше, чем 2.

Существует прием, позволяющий несколько лучше судить о согласии этих двух рядов чисел. Столбец (4) табл. II содержит числа столбца (2) «в накапливаемом виде». Например, рассмотрим строку, имеющую в столбце (1) число 7; в столбце (2) она имеет 5, а в столбце (4) — 8. при этом.

8 = 0 + 0 +0 + 1 +0 + 1 + 1 + 5,

т. е. 8 есть сумма, или «накопление» всех чисел, стоящих в столбце (2) каждое в своей строе, до числа 5 включительно. (Иными словами, 8 есть число тех лет этого периода, когда число рождений тройни не превосходило 7.) Столбец (5) содержит «в накапливаемом виде» числа столбца (3), и, таким образом, столбцы (4) и (5) выведены аналогичным образом, соответственно, из полученных из

298

наблюдения чисел в столбце (2 и теоретических чисел в столбце (3). Согласие между столбцами (4) и (5) выглядит блестяще; разность по абсолютной величине меньше, чем 1, исключая лишь один случай, где она, все же, меньше, чем 2.

6. Объяснение явлений. Идеи, связанные с понятием вероятности, играют известную роль в объяснении явлений, и это верно для явлений, относящихся к любой науке от физики до общественных наук. Рассмотрим два примера.

(1) Грегор Мендель (1822—1884), экспериментируя со скрещиванием растений, стал основателем новой науки генетики. Мендель был, кстати сказать, аббатом в Моравии и проводил свои эксперименты в саду монастыря. Его открытие, несмотря на свою важность, очень просто. чтобы его понять, нам нужно только описание одного эксперимента и интуитивное представление о вероятности. Чтобы еще облегчить нашу задачу, мы разберем не какой-либо из собственных экспериментов Менделя, а эксперимент, проведенный одним из его последователей[130].

Из двух близко родственных растений (разные виды одного и того же рода) одно имеет белые цветы, а другое — темно-красные. Эти два растения так близко родственны, что могут оплодотворять одно другое. Семена, получающиеся в результате такого скрещивания, развиваются в гибридные растения, имеющие промежуточный характер; гибриды имеют розовые цветы. (на рис. 14.3. красные изображены сильнее, а розовые — слабее затушеванными.) Если гибридные растения допускают самооплодотворение, то получающийся в результате семена развиваются в третье поколение растений, в котором представлены все три типа: имеются растения с белыми, растения с розовыми и растения с красными цветами. Рис. 14.3 схематически изображает отношения между тремя последовательными поколениями.

Однако наиболее поразительная особенность этого явления состоит в числовой пропорции, в которой появляются три различных типа растений третьего поколения. В описанном эксперименте наблюдалось 564 растения третьего поколения. Среди них те два типа растений, которые были похожи на то или другое прародительское растение, были приблизительно равночисленны: в третьем поколении имелось 141 растение с белыми цветами и 132 растения с красными цветами. Но растений, похожих на гибридные растения, было больше: в третьем поколении имелось 291 растение с розовыми цветами. Эти числа удобно окинуть взглядом на рис 14.3. Легко замечаем, что эти три числа, полученные с помощью эксперимента, находятся приближенно

в простой пропорции:

141 : 291 : 132, почти как 1 : 2 : 1.

Эта простая пропорция требует простого объяснения.

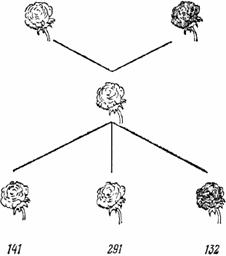
Рис. 14.3. Три поколения в эксперименте последователя Менделя[152].

Начнем с самого начала. Эксперимент начался со скрещивания двух различных типов растений. Любое цветковое растение возникает из объединения двух половых клеток (яйцеклетки и пыльцевого зерна). Розовоцветные[153] гибриды второго поколения возникли из двух половых клеток различного происхождения. Поскольку розовоцветные растения третьего поколения похожи на растения второго поколения, естественно допустить, что они, подобно второму поколению, были получены с помощью двух половых клеток различных типов. Это приводит нас к предположению, что розовоцветные гибриды второго поколения имеют два различных типа половых клеток. Однако допуская это, мы можем уловить возможность объяснения смешанного отпрыска. В самом деле, посмотрим внимательнее, что́ случилось бы, если бы розовоцветные гибриды второго поколения действительно имели два различных типа половых клеток, которые мы можем называть «белыми» и «красными» клетками. Когда комбинируются две такие клетки, возможна комбинация белой с белой или красной с красной или одного цвета с другим, и эти три различные комбинации могли бы объяснить три различных типа растений в третьем поколении; см. рис. 14.3.

После этого замечания не трудно будет объяснить числовые пропорции. Отклонение фактически наблюдавшейся пропорции 141 : 291 : 132 от простой пропорции 1 : 2 : 1 кажется случайным, т. е. оно выглядит похожим на отклонение полученных из наблюдений частот от лежащих в основании вероятностей. Это заставляет нас попытаться выяснить, каковы вероятности этих двух типов клеток или в какой пропорции производятся «белые» и «красные» клетки. Поскольку в третьем поколении имеется приблизительно столько же белоцветных, сколько и красноцветных растений, мы едва ли сможем

300

удержаться, чтобы не попробовать самое простое: допустим, что «белые» и «красные» половые клетки производятся розовоцветными растениями в равных количествах. В конце концов мы почти подведены к сравнению случайной встречи двух половых клеток со случайным вытаскиванием двух шаров и, таким образом, мы приходим к следующей простой задаче.

Имеется два мешка, содержащих белые и красные шары и ни одного шара другого цвета. Каждый мешок содержит ровно столько же белых, сколько и красных шаров. Обеими руками я вытаскиваю шары из обоих мешков, по одному шару из каждого. Найти вероятность вытаскивания двух белых шаров, двух шаров различного цвета и двух красных шаров.

Как легко видеть [см. § 3 (5)], искомые вероятности, соответственно, равны

Мы осознаем теперь простую причину пропорции 1 : 2 : 1, которая, по-видимому, лежит в основании полученных из наблюдения чисел, и при этом мы очень близко подходим к сущности представлений Менделя.

(2) Понятие случайного массового явления играет важную роль в физике. Чтобы проиллюстрировать эту роль, рассмотрим скорость химических реакций.

Сравнительно грубых наблюдений достаточно, чтобы натолкнуть на мысль, что скорость химического изменения зависит от концентрации реагирующих веществ. (Под концентрацией вещества мы понимаем его количество в единичном объеме.) Эта зависимость скорости химической реакции от концентрации реагентов была обнаружена рано, но открытие математической формы этой зависимости произошло намного позднее. Важный частный случай был подмечен Вильхельми в 1850 г., а общий закон был открыт двумя норвежскими химиками, Гульдбергом и Вааге, в 1867 г. сейчас мы наметим в частном случае и насколько сумеем просто некоторые из рассмотрений, которые привели Гульдберга и Вааре к их открытию.

Рассмотрим бимолекулярную реакцию. Это означает, что в реакции участвуют два различных вещества A и B, и реакция состоит в соединении одной молекулы первого вещества A с одной молекулой второго вещества B. Вещества A и B растворены в воде, и химическое изменение имеет место в этом растворе. Вещества, получающиеся в результате реакции, в дальнейшем в химической деятельности участия не принимают, они в том или ином отношении являются неактивными. Например, они могут быть не растворимы в воде и осаждаться в твердой форме.

Раствор, в котором имеет место реакция, состоит из очень большого числа молекул. В соответствии с идеями физиков (кинетиче-

301

ская теория материи) эти молекулы находятся в бешеном движении, перемещаются с различными скоростями, некоторые с очень высокой скоростью, и время от времени сталкиваются. Если молекула A сталкивается с молекулой B, то они могут настолько тесно сблизиться, что обменяются несколькими из своих атомов: химическая реакция, которой мы интересуемся, как мы себе представляем, состоит из такого обмена. Возможно, для такого обмена необходимо, чтобы молекулы могли сталкиваться с очень высокой скоростью или чтобы в момент столкновения они находились в благоприятном положении одна по отношению к другой. Как бы то ни было, чем чаще случается, что молекула A сталкивается с молекулой B, тем больше возможности для химического соединения двух таких молекул и тем выше будет скорость химической реакции. И, таким образом, мы приходим к предположению: скорость реакции пропорциональна числу столкновений между молекулами A и молекулами B.

Мы не могли бы точно предсказать число таких столкновений. Мы имеем перед собой случайное массовое явление, похожее на дождь. Вспомним рис. 14.2; там также мы не могли бы точно предсказать, сколько дождевых капель упадет на частичную площадь F. Однако мы могли бы предсказать, что число капель, падающих на частичную площадь, будет пропорционально числу капель, падающих на всю площадь P. (Пропорциональность является приближенной, и множитель пропорциональности, как указано в конце § 2, равен F/P.) Подобным же образом мы можем предсказать, что число столкновений, которыми мы интересуемся (между произвольной молекулой A и произвольной молекулой B), будет пропорционально также числу молекул A. Конечно, оно будет пропорционально также числу молекул B и, таким образом, в конечном счете пропорционально произведению этих двух чисел. Однако число молекул вещества пропорционально концентрации этого вещества, и поэтому наше предположение приводит к следующему утверждению: скорость реакции пропорциональна произведению концентраций.

Мы пришли к частному случаю общего закона действующих масс, открытого Гульдбергом и Вааге. Это — частный случай, соответствующий рассмотренным условиям. На основании закона действующих масс можно в любой данный момент вычислить концентрацию реагирующих веществ и предсказать все течение реакции.

7. Оценка статистических гипотез. Начнем с анекдота[131].

(1) «Однажды в Неаполе преподобный Галиани увидел человека из Базиликаты, который, встряхивая три игральные кости в чашке, держал пари, что выбросит три шестерки; и действительно он немедленно получил три шестерки. Вы скажете, что такая удача возможно. Однако человеку из Базиликаты это удалось во второй раз, и пари

302

повторилось. Он клал кости назад в чашку три, четыре, пять раз и каждый раз выбрасывал три шестерки. «Sangue di Bacco[132], — вскричал преподобный Галиани, — кости налиты свинцом». И так оно и было. Но почему его преподобие употребил нечестивое выражение?

Преподобный Галиани вывел правдоподобное заключение очень важного типа. Если он внезапно открыл для себя этот важный тип правдоподобного умозаключения, то его возбуждение вполне понятно, и я лично не упрекнул бы его за недостаточно благочестивое выражение.

Правильно будет к каждому относиться как к джентльмену, если нет каких-либо определенных доказательств противного. Совершенно таким же образом правильно будет участвовать в азартной игре при допущении, что она ведется честно. Я не сомневаюсь, что его преподобие поступал правильно и сначала допустил, что этот человек из Базиликаты имел честные кости и пользовался ими честно. Такое допущение, правильно сформулированное в терминах вероятности, является статистической гипотезой. Статистическая гипотеза, вообще, вводит (допускаемые ею) значения некоторых вероятностей. Так, его преподобие сначала в более или менее явной форме принял, что на любой из трех костей шесть очков будет выпадать с вероятностью 1/6. (Мы имеем здесь в точности ту же статистическую гипотезу, что и в § 5 (1).)

Исчисление вероятностей позволяет нам вычислить искомые вероятности по данным вероятностям на основании данной статистической гипотезы. Так, на основании статистической гипотезы, принятой его преподобием сначала, мы можем вычислить вероятность выпадения на трех костях трех шестерок; она равна

(1/6)³ = 1/216,

— довольно малая вероятность. Вероятность повторения этого фокуса два раза, т. е. выпадения трех шестерок и в первом, и во втором испытании, равна

(1/216)² = (1/6)⁶ = 1/46 656;

действительно, это очень маленькая вероятность, однако человек из Базиликаты повторил эту необычайную ведь пять раз. Запишем соответствующие вероятности

Повторения	Вероятность
1	1/6^3 = 1/216
2	1/6^6 = 1/46 656
3	1/6^9 = 1/10 077 696
4	1/6^12 = 1/2 176 782 336
5	1/6^15 = 1/470 184 984 576

303

Возможно, преподобный Галиани принял свое первоначальное допущение из простой вежливости; глядя на человека из Базиликаты, он, быть может, имел сомнения в отношении честности костей. Его преподобие сохранял молчание, пока три шестерки выпали последовательно дважды, событие, которое при исходном допущении должно было бы произойти не намного чаще, чем один раз за пятьдесят тысяч испытаний. Он сохранял молчание даже дольше. Однако когда события становились все более и более невероятными, достигли и возможно превзошли ту степень невероятия, которую люди рассматривают как сверхъестественную, его преподобие потерял терпение, вывел свое заключение, отказался от первоначального допущения и энергично высказался[154].

(2) Анекдот, который мы только что обсудили, интересен только в одном отношении: он типичен. Он ясно показывает обстоятельства, при которых мы можем разумно отказаться от статистической гипотезы. Специальный интерес вызывают следствия, касающиеся какого-либо события, которое с точки зрения нашей статистической гипотезы выглядит как очень невероятное[155]; я имею в виду события, вероятность которых, вычисленная на основании этой статистической гипотезы, очень мала. Теперь мы обращаемся к опыту: мы наблюдаем испытание, которое может вызвать это якобы невероятное событие. Если это событие несмотря на его вычисленную низкую вероятность в действительности произошло, то оно дает сильный аргумент против предложенной статистической гипотезы. В самом деле нам трудно поверить, что могло произойти нечто столь невероятное. Однако неоспоримо — оно все-таки произошло. Тогда мы ясно осознаем, что любая вероятность вычисляется на основании некоторой статистической гипотезы, и начинаем сомневаться в правильности основания, на котором было построено наше вычисление столь малой вероятности. И таким образом возникает аргумент против первоначальной статистической гипотезы.

(3) Как и преподобный Галиани, мы также почувствовали себя обязанными отвергнуть гипотезу честных костей, когда исследовали обширные наблюдения, приведенные в § 5 (1); наши доводы для того, чтобы ее отвергнуть, были, однако, не совсем такие отчетливые, как его. Не могли бы мы в свете предыдущего обсуждения найти лучшие доводы?

Вот факты: из 315 672 попыток выбросить игральными костями пять или шесть очков было 106 602 случая успеха; см. § 5 (2). Если бы все бросавшиеся кости были честными, то вероятность успеха была бы равна ⅓. Поэтому мы должны были ожидать приблизительно

315 672/3 = 105 224

успеха из 315 672 испытаний. Таким образом, число, полученное из наблюдений, отклоняется от ожидаемого числа на

106 602 —105 224 = 1378

304

единиц. Говорит ли такое отклонение за или против гипотезы честных костей? Должны ли мы рассматривать отклонение 1378 как маленькое или как большое? Вероятность такого отклонения высока или низка?

Последний вопрос, по-видимому, имеет смысл. Однако мы нуждаемся еще в разумном истолковании короткого, но важного слова «такое». Мы отвергнем статистическую гипотезу, если вероятность, вычислением которой мы интересуемся окажется низкой. Однако вероятность того, что отклонение будет в точности равно 1378 единиц во всяком случае очень мала — была бы очень мала даже вероятность того, чтобы отклонение точно равнялось 0. Поэтому мы должны принять в расчет все отклонения по абсолютной величине не меньшие, чем наблюдаемое отклонение 1378. И, таким образом, наше суждение зависит от решения следующей задачи. Дано, что вероятность успеха равна ⅓ и что испытания независимы; найти вероятность того, что в 315 672 испытаниях число успехов будет больше, чем 106 601[156] или меньше, чем 103 847.

Зная немного исчисление вероятностей, мы находим, что искомая вероятность приближенно равна

0,0000001983;

это, значит, меньше чем два шанса на десять миллионов. Иными словами, произошло событие, которое выглядит крайне невероятным, если принять статистическую гипотезу, лежащую в основании нашего вычисления вероятности. Нам трудно поверить, что такое невероятное событие действительно произошло, и, таким образом, представляется крайне невероятной лежащая в основании гипотеза честных костей. Уже в § 5 (1) мы видели достаточные основания отвергнуть гипотезу честных костей, но теперь мы видим еще лучшее, более ясное основание отказаться от нее.

(4) Действительное появление события, которому некоторая статистическая гипотеза приписывает маленькую вероятность, является аргументом против этой гипотезы, и чем меньше вероятность, тем сильнее аргумент.

Для того чтобы ясно себе представить это существенное обстоятельство, рассмотрим последовательность

Из статистической гипотезы следует, что вероятность некоторого события равна ¹/₁₀. Событие происходит. Должны ли мы отказаться от этой гипотезы? При обычных обстоятельствах большинство из нас не чувствовало бы себя вправе от нее отказаться; аргумент против гипотезы не кажется еще достаточно сильным. Если происходит другое событие, которому статистическая гипотеза приписывает вероятность ¹/₁₀₀, то стимул для отказа от этой гипотезы

305

становится более сильным. Если предполагаемая вероятность равна ¹/₁₀₀₀ и тем не менее событие происходит, то доводы против гипотезы становятся еще сильнее. Если статистическая гипотеза приписывает событию вероятность

или один шанс на миллиард и тем не менее событие происходит, то почти каждый стал бы рассматривать эту гипотезу как безнадежно дискредитированную, хотя и не существует никакой логической необходимости отказаться от гипотезы именно на этом основании. Если, однако, эта последовательность продолжается без перерыва, так что одно за другим происходят события, которым статистическая гипотеза приписывает вероятности, монотонно убывающие до 0, то для каждого разумного человека раньше или позже наступает критический момент, когда ему представляется оправданным отказаться от гипотезы, сделавшейся несостоятельной из-за все более и более невероятных следствий. И именно это обстоятельство ясно подсказывается историей преподобного Галиани. Вероятность первого выпадения трех шестерок была равна 1/216; а вероятность последовательности пяти выпадений каждый раз трех шестерок равна 1/470 184 984 576.

Предыдущее обсуждение имеет для нас особую важность, если мы принимаем точку зрения, согласно которой теория вероятностей является частью науки о природе. Любая естественная наука должна возвращаться к наблюдениям. Поэтому она должна принимать правила, как-то определяющие те условия, при соблюдении которых ее утверждения считаются подтвержденными или опровергнутыми опытом. Именно это мы и сделали для теории вероятностей. Мы описали некоторые условия, при соблюдении которых разумно можем рассматривать статистическую гипотезу как практически опровергнутую наблюдениями. С другой стороны, если статистическая гипотеза выдержала несколько возможностей опровержения, мы можем рассматривать ее как до некоторой степени подтвердившуюся.

(5) Вероятность, как она определена в § 2, есть теоретическое значение относительной частоты дальнего действия. Предыдущее дало нам возможность ясно понять несколько вещей. Во-первых, теоретическое значение зависит, конечно, от нашей теории, от наших исходных допущений, от принятой статистической гипотезы. Во-вторых, такое теоретическое значение может очень сильно отличаться от действительного значения.

Подходящие обозначения могут помочь нам пояснить наши идеи. Пусть P — вероятность события E, вычисленная на основании некоторой статистической гипотезы H. Тогда P зависит и от E и от H. (Фактически мы могли бы вместо P пользоваться более явным символом P(E, H), подчеркивающим зависимость P от E и H.[157])

306

В некоторых из предыдущих приложений мы принимали гипотезу H (по крайней мере на время) как не требующую доказательства и, вычисляя P на основании H, пытались предсказать доступную наблюдению частоту события E. Однако в этом параграфе мы шли в другом направлении. Понаблюдав за наступлением события E, мы вычисляли P на основании статистической гипотезы H и, принимая во внимание полученное значение P, пытались оценить надежность гипотезы H. Мы ощущаем здесь новую сторону вероятности P. Чем меньше P, тем большую склонность мы чувствуем отказаться от гипотезы H и тем более неправдоподобной кажется нам гипотеза H: P указывает правдоподобие гипотезы H. Мы будем, начиная с этого момента, говорить, что P есть правдоподобие статистической гипотезы H, оцененное, принимая во внимание тот факт, что событие E наблюдалось[158].

Эта терминология, по существу согласующаяся со словоупотреблением статистиков, подчеркивает одну сторону зависимости P от события E и статистической гипотезы H. Наша первоначальная терминология делала ударение на другой из этих двух сторон той же самой зависимости: P есть вероятность события E, вычисленная на основании статистической гипотезы H.

Нужна некоторая практика в употреблении этой двойной терминологии, чтобы убедить нас в том, что ее преимущества достаточно перевешивают ее опасности.

8. Выбор между статистическими гипотезами. Следующий пример может обеспечить первую ориентировку в приложениях теории вероятностей в статистическом исследовании.

(1) Потребитель покупает у производителя некоторое изделие большими партиями. Этот потребитель является крупным потребителем, крупным торговцем или промышленной фирмой или правительственным агентом. Производитель также является крупным и производит указанное изделие в большом масштабе. Это изделие может быть гвоздем или кнопкой или каким-нибудь другим промышленным товаром; интересным примером является фитиль, используемый для воспламенения взрывчатого вещества в боеприпасах или при подрывных работах[159]. Изделие должно удовлетворять некоторым условиям. Например, гвоздь должен быть не длиннее чем 2,04 дюйма, не короче, чем 1,96 дюйма, аналогичным образом должна быть обусловлена его толщина и, возможно, его минимальное разрушающее напряжение, обусловливается время сгорания фитиля и т. д.[160] Изделие, не удовлетворяющее этим условиям, рассматривается как дефектное. Даже наиболее тщательно изготовленная партия может содержать небольшую долю дефектных изделий. Поэтому прежде чем партия перейдет от производителя к потребителю, она должна быть проверена. Партия может быть проверена полностью, т. е. может быть испытано, удовлетворяет ли требуемым условиям каждое изделие в этой

307

партии. Такая сплошная проверка была бы непрактичной для партии из 10 000 гвоздей и абсурдной для партии фитилей, даже если бы эта партия была невелика; чтобы измерить время сгорания фитиля, вы должны были бы его сжечь, и не было бы большого смысла в том, чтобы при проверке уничтожить всю партию. Поэтому во многих случаях вместо проверки перед приемкой всей партии из этой партии делается небольшая выборка. Простая процедура такой приемки, основанная на выборочном контроле, характеризуется следующим правилом.

«Произведем случайную выборку n изделий из представленной на рассмотрение партии, состоящей из N изделий. Испытаем каждое изделие из этой выборки. Если число дефектных изделий в выборке не превышает некоторого согласованного числа c, так называемого приемочного числа, то потребитель партию принимает, но он от нее отказывается и производитель берет ее обратно, если в выборке дефектных изделий больше, чем c».

Результаты, получаемые с помощью этого правила, зависят от случая. Случайно доля дефектных изделий в выборке может оказаться значительно ниже или значительно выше, чем во всей партии. Если выборка лучше, чем вся партия, то случай работает против потребителя, но если выборка хуже, чем вся партия, то он работает против производителя. Несмотря на этот риск, некоторая процедура такого типа кажется необходимой, и сформулированное правило может быть вполне разумным. Мы должны выяснить, как действует эта процедура, как ее результат зависит от качества представленной партии. И, таким образом, мы приходим к формулировке следующей задачи:

Дана вероятность p того, что выбранное наугад в рассматриваемой партии изделие является дефектным; найти вероятность a того, что партия будет принята.

В наиболее важных на практике случаях объем партии, N, велик даже по сравнению с объемом выборки, n. В подобных случаях мы можем допустить, что N бесконечно; мы мало потеряем в точности и много выиграем в простоте. Допуская, что N = ∞, легко находим

Примем это выражение для a, вероятности приемки, без доказательства и сосредоточим свое внимание на обсуждении некоторых его практических приложений.

Начертим график вероятности a как функции p; см. рис 14.4. если бы мы начертили график 100a как функции 100p, то форма кривой осталась бы без изменений. Но 100p есть процент дефектных изделий в рассматриваемой партии. С другой стороны, если бы несколько партий с одним и тем же процентным содержанием

308

дефектных изделий были подвергнуты одной и той же процедуре проверки, то относительная частота приемки, т. е. отношение числа принятых партий к числу представленных на рассмотрение партий, была бы близка к a. Следовательно, в конечном счете 100a будет процентом принятых партий среди представленных на рассмотрение партий. Это объясняет наименование осей на рис. 14.4. Кривая на рис. 14.4. позволяет нам обозреть, какое влияние оказывает эта процедура на партии различного качества, и, таким образом, ее правильно называть оперативной характеристикой.

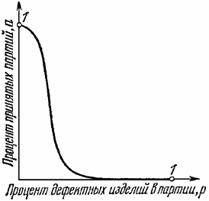
Рис. 14.4. Оперативная характеристика процедуры приемки, основанной на выборочном контроле.

Если судить по результатам этой процедуры, кажется ли она разумной? Вот вопрос, который мы хотим рассмотреть.

Если в партии дефектных изделий нет, то не должно быть никаких шансов, чтобы она была отвергнута. Действительно, если p = 0, то наша формула, как и должно быть, дает a = 1. Если в партии имеются только дефектные изделия, то не должно быть никаких шансов, чтобы она была принята. Действительно, если p = 1, то наша формула, как и должно быть, дает a = 0. Обе крайние точки графика оперативной характеристики, очевидно, разумны.

Если число дефектных изделий возрастает, вероятность приемки должна убывать. Действительно, дифференцируя с некоторым умением, легко находим удивительно простое выражение

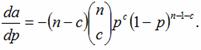
Производная всегда отрицательна, следовательно, оперативная характеристика необходимо является убывающей кривой, как и изображено на рис. 14.4, который вновь оказался таким, как и следовало.

Абсолютная величина производной, или — da/dp, также имеет некоторое практическое значение. Дифференциал dp абсциссы представляет изменение качества партии. Дифференциал da ординаты представляет изменение шансов приемки, производимое изменением качества. Чем больше отношение этих изменений da/dp по абсолютной величине, тем более резкое различие делает наша процедура между двумя мало различающимися партиями. В особенности точку, в которой da/dp достигает максимума своей абсолютной величины, правильно называть «точкой наиболее резкого различения». Эту точку легко узнать на графике: она является точкой перегиба, если

309

такая существует, а в противном случае — левым концом кривой. (Ее абсцисса p = c/(n — 1).)

(2) Это правило кажется разумным и с другой точки зрения. Оно имеет известную гибкость. Выбором n, объема выборки, и c, приемочного числа, мы можем приспособить это правило к конкретным требованиям. И потребитель, и производитель требуют предохранения от риска, связанного с выбором. Плохая партия иногда может дать хорошую выборку, а хорошая партия — плохую, и, таким образом, существует два вида риска: процедура выбора может принять плохую партию и забраковать хорошую партию. Потребитель против приемки плохой партии, а производитель против браковки хороших партий. Однако оба вида нежелательных решений время от времени обязательно случаются и единственное, что мы можем разумно требовать, состоит в том, чтобы они не случались слишком часто. Это требование ведет к конкретным задачам вроде следующей:

«Определить объем выборки и приемочное число так, чтобы имелся менее чем один шанс на десять, что будет принята партия с 5% дефектных изделий, и менее чем пять шансов на сто, что будет забракована партия только с 2% дефектных изделий».

В этой задаче два неизвестных: объем выборки n и приемочное число c. Условие задачи требует выполнения следующих двух неравенств:

a > 0,95, когда p = 0,02,

a < 0,1, когда p = 0,05.

Можно одновременно удовлетворить обоим этим условиям, но, чтобы найти наименьший объем n и соответствующее приемочное число c, для которых имеют место требуемые неравенства, нужна значительная вычислительная работа.

Мы не будем заниматься этой вычислительной работой. Мы гораздо больше заинтересованы здесь в том, чтобы ясно представить себе эту задачу, чем в том, чтобы ее решить. Остановимся поэтому еще немного на некоторых связанных с ней обстоятельствах. Как мы уже сказали, нежелательны и принятие плохой партии, и браковка хорошей партии: первое — с точки зрения потребителя, а второе — с точки зрения производителя. Однако эти две нежелательные возможности могут быть неодинаково нежелательны и интересы потребителя и производителя могут оказаться не столь уж резко противоположными. Принятие плохой партии не совсем в интересах производителя; оно может повредить его репутации. Но браковка хорошей партии может очень сильно идти против интересов потребителя; он может срочно нуждаться в изделиях, браковка может быть причиной значительной задержки. Кроме того, повторная браковка хорошей партии или даже опасность такой браковки может повысить цену. Если принять во внимание интересы обеих сторон, то браковка хорошей партии может быть еще менее желательной,

310

чем принятие плохой партии. На этом фоне, по-видимому, разумно то, что условия нашей задачи обеспечивают большее предохранение от браковки партии лучшего качества, чем от принятия партии худшего качества. (Для первого нежелательного события допускаются только 5 шансов на сто, а для второго — 10 шансов на сто.)

(3) Задача, рассмотренная в (2), допускает другую, несколько отличную от прежней, интерпретацию.

Юрисконсульт производителя утверждает, что в партии имеется не более чем 2% дефектных изделий. Однако юрисконсульт потребителя настаивает на том, что в партии имеется по крайней мере 5% дефектных изделий. По какой-либо причине (это может быть партия фитилей) полная проверка невозможна; поэтому решить, какое из этих двух утверждений верно, должна какая-то процедура, основанная на выборе. Для этой цели можно подходящим образом воспользоваться процедурой, намеченной в (1), с числовыми данными, указанными в (2).

Действительно, противоречащие утверждения двух юрисконсультов подсказывают идею. Мы можем допустить, что в отношении партии имеются ровно две возможности: процент дефектных изделий в партии или в точности равен 2% или в точности равен 5%. Конечно дефектных изделие менее желательна, чем принятие, никто такой выдумке не поверит, но статистик может найти ее удобной: она ограничивает его задачу выбором между двумя ясными и простыми альтернативами. Если стороны согласны, что браковка партии с 2% дефектных изделий менее желательна, чем принятие партии с 5% дефектных изделий, то статистик может разумно принять процедуру, намеченную в (1), с числовыми данными, предписанными в (2). Удовлетворит ли выбор статистика юрисконсультов или философов, я не рискую сказать, но он, несомненно, имеет ясную связь с рассматриваемыми фактами. Правило статистика, примененное к большому числу аналогичных случаев, принимает хорошую партию (с 2% дефектных изделий) приблизительно 950 раз из 1000 и бракует ее только 50 раз, но это правило бракует плохую партию (с 5% дефектных изделий) приблизительно 900 раз из 1000 и принимает ее приблизительно только 100 раз. Иными словами, нельзя ожидать, что правило статистика, основанное на выборе, каждый раз даст правильное решение, но можно разумно ожидать, что оно даст правильное решение в назначенном проценте случаев в конечном счете.

(4) Дать адекватную идею того, что делают статистики, на основании одного лишь примера — это, конечно, безнадежное предприятие. Однако, пользуясь предыдущим примером, мы можем получить представление о задаче статистика, которое, несмотря на свою неполноту, будет не так уж сильно искажено: статистик составляет правила той же природы, что и процедура приемки, основанная на выборочном контроле, намеченная в (1) и рассмотренная в связи с числовыми данными в (2). Мы можем понять задачу статистика,

311

если поняли природу правил, которые он составляет. Поэтому мы должны в общих терминах сформулировать то, что кажется существенным в нашем частном правиле; я имею в виду правило, которое мы обсуждали в предыдущих пунктах (1), (2) и (3). Наше правило предписывает выбор между двумя решениями: принятием и браковкой. Однако задача в форме, рассмотренной в (3), более пригодна для обобщения. Там мы рассматривали выбор между двумя статистическими гипотезами. (Вот они: «эта случайная выборка берется из большой партии с 2% дефектных изделий» и «эта случайная выборка берется из большой партии с 5% дефектных изделий».о) Любой разумный выбор должен быть сделан с надлежащим учетом предыдущего опыта и будущих следствий. Действительно, наше правило составляется с учетом и того, и другого.

В соответствии с нашим правилом выбор зависит от множества ясно обусловленных наблюдений (испытание n изделий и число дефектных изделий, обнаруженных среди n испытанный изделий). Эти наблюдения образуют подходящий опыт, на котором основывается выбор. Поскольку наше правило отдает предпочтение одной гипотезе по сравнению с другой на основании наблюдений, его с полным правом можно называть индуктивным правилом.

Наше правило составляется, чтобы с его помощью находить вероятные следствия. Статистик не может предсказать следствия любого отдельного приложения правила. Он предвидит только как правило будет работать в конечном счете. Если выбор, предписанный правилом, производится много раз в таких-то условиях, то он в конечном счете приведет к такому-то результату в таком-то проценте испытаний. Наше правило составляется, чтобы с его помощью находить следствия дальнего действия.

Если подвести итоги, наше правило составляется для того, чтобы делать выбор между статистическими гипотезами, оно основывается на обусловленном множестве наблюдений и имеет целью получить следствия дальнего действия. Если мы можем рассматривать наше правило как достаточно типичное, то мы имеем представление о том, что делает статистики: они составляют правила этого рода.

(В действительности они пытаются придумать «наилучшее» правило этого рода. Например, они хотят сделать шансы такого-то нежелательного эффекта минимальными при заданном объеме выборки, от которого зависят труд и расходы, необходимые для наблюдений.)

(5) Взятие из партии случайной выборки в статистическом исследовании является важной операцией. Имеется другая задача, связанная с этой операцией, которую мы должны здесь обсудить. В формулировке задачи мы сохраняем свои предыдущие обозначения.

В очень большой партии 100p процентов изделий являются дефектными. Чтобы получить некоторую информацию относительно p, мы берем выборку из n изделий, среди которых

312

находим m дефектных изделий. Какое значение мы должны были бы разумно приписать p, на основании этого наблюдения?

Есть очевидный ответ, подсказываемый самим определением вероятности. Однако задача важна и заслуживает, чтобы ее исследовали под различными углами зрения.

Наше наблюдение дает некоторую информацию относительно p. В частности, если m оказалось отличным от 0, то мы заключаем, что p отлично от 0. Подобным же образом, если m меньше, чем n, то мы заключаем, что p меньше, чем 1. Однако как бы то ни было, p остается неизвестным, и в качестве p могут быть взяты все значения между 0 и 1. Если мы приписываем p одно из этих значений, то мы делаем догадку, принимаем предположение, выбираем статистическую гипотезу.

Перед тем как мы сделаем наш выбор, подумаем о следствиях этого выбора. Если мы имеем для p какое-нибудь значение, то мы можем вычислить вероятность того события, наблюдение которого является нашим существенным данным. Я имею в виду вероятность появления точно m дефектных изделий в случайной выборке, состоящей из n изделий. Обозначим эту вероятность буквой P. Тогда

Значение вероятности P зависит от p, меняется вместе с p, может быть больше или меньше. Если бы, однако, эта вероятность P наблюденного события оказалась очень малой, мы должны были бы отвергнуть лежащую в основании статистическую гипотезу. Было бы глупо выбрать такую неправдоподобную статистическую гипотезу, от которой немедленно приходится отказаться. Выберем поэтому наименее неправдоподобную гипотезу, ту гипотезу, для которой опасность ее отвергнуть является наименьшей. Иначе говоря, выберем значение p, для которого P является насколько возможно большим.

Теперь, если P максимально, то максимально и ln P, следовательно,

Это уравнение дает

Таким образом, после некоторого рассмотрения мы сделали выбор, который соблазнялись сделать с самого начала: в качестве разумного приближения для p, т. е. для лежащей в основании вероятности, мы выбираем m/n, полученную из наблюдения относительную частоту.

Но наше рассмотрение не было простой уловкой. Мы можем на этом рассмотрении многому научиться.

313

Начнем с исследования роли P. P есть вероятность некоторого наблюденного события E (m дефектных изделий в выборке объема n). Эта вероятность вычисляется на основании статистической гипотезы H_p, состоящей в том, что 100p есть процент дефектных изделий в партии. вероятность P изменяется вместе с гипотезой H_p (со значением p). Чем меньше P, тем менее приемлемой, менее правдоподобной кажется H_p. Таким образом, мы приходим к рассмотрению P в качестве указателя правдоподобия гипотезы H_p. Термин «правдоподобие» был введен ранее [в § 7 (5)] в том же самом смысле, но теперь мы можем яснее видеть, чем мотивируется его введение.

Подчеркнем, что мы выбираем среди различных допустимых статистических гипотез H_p (с 0 ≤ p ≤) ту, для которой P, правдоподобие H_p, является насколько возможно большим. За этим выбором стоит принцип, который правильно назвать принципом максимального правдоподобия и которым статистик руководствуется и в других случаях, менее очевидных, чем наш случай.

9. Оценка нестатистических предположений. Рассмотрим несколько примеров, чтобы с различных точек зрения проиллюстрировать одну и ту же основную ситуацию.

(1) Однажды я познакомился с неким м-ром Моргенштерном. Эта фамилия не очень обычна[161], но не является для меня неизвестной. Существовал немецкий писатель Моргенштерн, к бессмысленной поэзии которого я питал большую симпатию. Ах да, мой двоюродный брат, живущий в Атланте, штат Джорджия, недавно начал работать в конторе «Марк Моргенштерн и К°, инженеры-консультанты».

В начале я ничего не думал о м-ре Моргенштерне. Однако через некоторое время я услышал, что он занимается инженерным делом. Затем просочилась другая информация. Я услышал, что имя моего нового знакомого Марк и что место его работы — Атланта, штат Джорджия. На этом этапе очень трудно не поверить, что мой двоюродный брат работает у этого м-ра Моргенштерна. Я прямо спросил м-ра Моргенштерна и убедился в том, что так оно и есть.

Эта тривиальная маленькая история очень поучительна. (Она основана, между прочим, на действительном опыте, но имена, конечно, изменены, как и некоторые не относящиеся к делу обстоятельства.) Не невероятно, чтобы два различных человека имели точно одну и ту же фамилию, если эта фамилия очень распространена, как Джонс или Смит. Более невероятно, чтобы два различных человека имели одни и те же имя и фамилию, особенно когда это нераспространенные имя и фамилия, как Марк Моргенштерн. Чтобы два различных человека имели одну и ту же профессию или жили в одном и том же большом городе, не невероятно. Однако очень невероятно, чтобы два различных человека, взятых наугад, имели одну и ту же необычную

314

фамилию, жили в одном и том же городе и имели одно и то же занятие. Случайному совпадению было трудно поверить, и, таким образом, мое предположение о моем новом знакомом, м-ре Моргенштерне, было вполне разумно. Оно оказалось правильным, но это в действительности имеет небольшое отношение к существу дела. Мое предположение было разумно, законно, оправдано на основании рассматриваемых вероятностей. Даже если бы мое предположение оказалось неправильным, у меня не было бы причины стыдиться его.

В этом примере не дано никакого числового значения для вероятности, решающим образом связанной с задачей, но грубая оценка для нее могла бы быть с некоторым трудом получена.

(2) Два друга, неожиданно встретившись, решили написать открытку третьему другу. Однако они были не совсем уверены в адресе. Оба помнили город (это был Париж) и улицу (это был бульвар Распайль[162]), но оба они не помнили точно номера[163] дома. «Подожди, — сказал один из друзей, — подумаем о номере не разговаривая, и каждый из нас пусть запишет номер, когда решит, что он его вспомнил». Это решение было принято, и оказалось, что оба друга вспомнили один и тот же номер: бульвар Распайль, 79. Они написали этот адрес на открытке, и открытка пришла к третьему другу. Адрес был правильным.

Однако какие основания были принять номер 79? Не разговаривая между собой, два друга вспомнили независимо. Оба они знали, что бульвар Распайль достаточно длинен, чтобы иметь здания с номерами по крайней мере до 100[164]. Поэтому кажется разумным предположить, что вероятность случайного совпадения двух чисел не больше ¹/₁₀₀. Но эта вероятность мала, и, таким образом, гипотеза о случайном совпадении кажется неправдоподобной. Отсюда уверенность в номере 79.

(3) Согласно утверждению банка, баланс моего лицевого счета в конце прошлого месяца составлял 331 доллар 49 центов. Я вычислил свой баланс на ту же дату на основании своих заметок и нашел ту же самую сумму. Согласие этих двух вычислений привело меня к убеждению, что сумма, относительно которой они были в согласии, правильно. Несомненно ли это? Никоим образом. Хотя оба вычисления привели к одному и тому же результату, этот результат мог бы оказаться ошибочным, а согласие могло быть случайным. Правдоподобно ли это?

Эта сумма, выраженная в центах, является пятизначным числом. Если последняя его цифра была выбрана наугад, то она могла в такой же мере быть как 0, 1, или 2, или 8, так и 9, и, таким образом, вероятность того, что последняя цифра есть 9, равна ¹/₁₀. Это же верно для каждой другой цифры. Действительно, если все цифры выбраны наугад, то наше число может быть любым из следующих

000,00, 000,01, 000,02, …, 999,99.

315

Я, очевидно, имею здесь 100 000 чисел. Если моя система из пяти цифр, 33149, была получена каким-либо чисто случайным путем, то в равной мере могли бы возникнуть все такие системы. И так как имеется 100 000 таких систем, то вероятность того, что будет получена какая-нибудь наперед заданная система, равна

Но 10^-5 = 0,00001 — очень маленькая вероятность. Если, пытаясь получить эффект с такой маленькой вероятностью, кто-нибудь ухитрится добиться успеха в самом первом испытании, то его исход легко может показаться сверхъестественным. Я, однако, не склонен верить, что в моем скромном банковском счете есть что-либо сверхъестественное. Случайному совпадению трудно поверить, и поэтому я вывел заключение, что согласие двух вычислений объясняется правильностью результата. Обычные, нормальные люди вообще так и думают в сходных обстоятельствах, и после предыдущих рассмотрений мнение такого рода представляется довольно разумным.

(4) С каким языком теснее связан английский язык, с венгерским или польским? Чтобы ответить на этот вопрос, достаточно очень небольших лингвистических познаний, но, разумеется забавнее получить ответ собственными силами, чем принять его, опираясь на авторитет какой-либо книги. Вот основанный на здравом смысле подход к ответу.

И форма, и значение слов на протяжении истории изменяются. Первое можно понять, если обратить внимание на то, что слова одного и того же языка по-разному произносятся в различных местностях, а второе, если сообразить, что значение слов не жестко закреплено, а колеблется и меняется вместе с контекстом. Во втором отношении существует, однако, бросающееся в глаза исключение: значение наименований чисел один, два, три, … понемногу, без скачков изменяться, конечно, не может. Это — достаточное основание подозревать, что наименования чисел на протяжении истории языков своего значения не изменяли. Будем основывать поэтому первое сравнение указанных языков на одних лишь наименованиях чисел. В табл. III записаны наименования первых десяти чисел на английском, польском, венгерском и семи других современных европейских языках. Рассматриваются только языки, пользующиеся латинским алфавитом (это объясняет отсутствие русского и современного греческого языка). Некоторые диакритические знаки (ударения, седили[165]), неизвестные в английском языке, опускаются (в шведском, немецком, польском и венгерском).

Рассматривая табл. III и наблюдая, как пишутся одни и те же числа в разных языках, мы легко подмечаем различные сходства и совпадения. Первые пять языков (английский, шведский, датский, голландский и немецкий) кажутся довольно сходными один с другим,

316

Англий- ский	Швед- ский	Датский	Голланд- ский[166]	Немец- кий	Фран- цузский	Испан- ский	Италь- янский	Поль- ский	Венгер- ский
one	en	en	een	ein	un	uno	uno	jeden	egy
two[167]	tva	to	twee	zwei	deux	dos	due	dwa	ketto
three	tre	tre	drie	drei	trois	Tres	tre	trzy	harom
four	fyra	fire	vier	vier	quatre	cuatro	quattro	cztery	negy
five	fem	fem	vijf	funf[168]	cinq	cinco	cinque	piec	ot
six	sex	seks	zes	sechs	six	seis	sei	szesc	hat
seven	sju	syv	zeven	sieben	sept	siete	sette	siedem	het
eight	attta	otte	acht	acht	huit	ocho	otto	osiem	nyolc
nine	nio	ni	negen	Neun	neuf	nueve	nove	dziewiec	kilenc
ten	tio	ti	tien	zehn	dix	diez	dieci	dzeisiec	tiz

а следующие три языка (французский, испанский и итальянский), по-видимому, находятся даже в еще более тесном согласии; таким образом, мы имеем две группы: одна состоит из пяти¸ а другая: одна состоит из пяти, а другая из трех языков. Однако даже эти две группы кажутся как-то связанными друг с другом; заметьте совпадение написаний 3 на шведском, датском и итальянском и написание 6 на английском и французском языках. Польский язык кажется в одних отношениях ближе к одной группе, а в других — с другой; ставните 2 в шведском и польском, 7 в испанском и польском. Но венгерский не обнаруживает таких совпадений ни с одним из других девяти языков. Эти наблюдения приводят к впечатлению, что венгерский язык мало связан с девятью другими языками, которые все как-то связаны между собой. В частности, и это является ответом на наш первоначальный вопрос, английский язык, по-видимому, определенно теснее связан с польским, чем с венгерским языком[169].

Однако имеется несколько возражений. Первое возражение состоит в том, что «сходство» и «согласие» — неясные слова; нам следовало бы точнее сказать, что мы имеем в виду. Это возражение указывает правильное направление. Следуя его совету, мы принесем в жертву часть наших доводов, чтобы сделать остальную часть более точной. Рассмотрим только начальные буквы наименований чисел, записанных в табл. III. Сравним два слова, выражающих одно и то же число на двух различных языках; назовем их находящимися в «согласии», если они имеют одно и ту же начальную букву, и в «разногласии», если их начальные буквы различны. Таблица IV содержит число случаев согласия для каждой пары языков. Например, число 7 в той же строке, что и буквы «Исп.», и в том же столбце, что и буквы «Польск.» указывает, что испанский и польский языки имеют ровно семь чисел, находящихся в согласии, из десяти воз-

317

можных случаев. Читателю следует проверить это и несколько других чисел в табл IV. Последний столбец табл IV показывает, сколько вообще случаев согласия имеет каждый язык с девятью другими языками. Этот последний столбец очень ясно показывает изолированное положение венгерского языка: он имеет вообще только 8 случаев согласия, тогда как для других девяти языков число случаев согласия колеблется между 22 и 46.

Таблица IV

Согласие начальных букв наименований чисел на десяти языках

Англ	8	8	3	4	4	4	4	3	1	39
	Шв.	9	5	6	4	4	4	3	2	45
		Дат.	4	5	4	5	5	4	2	46
			Гол.	5	1	1	1	0	2	22
				Нем.	3	3	3	2	1	32
					Фр.	8	9	5	0	38
						Исп.	9	7	0	41
							Ит.	6	0	41
								Польск.	0	30
									Венг.	8

Однако, пожалуй, любое определенное заключение, полученное из таких данных, было бы поспешным: совпадение начальных букв могло быть вызвано случайностью. Это возражение легко возникает, но на него столь же легко ответить. Случай может проникнуть в нашу картину через различные каналы. Может существовать элемент случайности, проистекающий из того факта, что соответствие между буквами и произношением никоим образом не является жестким. Это верно даже для одного языка (особенно английского). Тем более одна и та же буква часто довольно различно произносится в различных языках и, с другой стороны, различные буквы иногда произносятся очень сходно. Мы должны допустить, что наблюдаемые совпадения несвободны от некоторого элемента случайности. Однако вот в чем вопрос: вероятно ли, чтобы такие совпадения, как те, которые мы наблюдали, были вызваны простой случайностью?

Если мы желаем ответить на этот вопрос точно, численно, то должны принять какую-либо точную, численно определенную статистическую гипотезу и вывести из нее следствия. Которые можно было бы сопоставить с наблюдениями. Однако выбор подходящей гипотезы не слишком очевиден. Рассмотрим здесь две различные статические гипотезы.

I. Имеется два мешка. Каждый мешок содержит по 26 шаров, каждый шар помечен буквой латинского алфавита, и различные шары одного и того же мешка помечены различными буквами. Обеими руками я вытаскиваю шары одновременно из обоих мешков, по

одному шару из каждого мешка. Две буквы, вытащенные таким образом, могут совпадать или нет; их совпадение уподобляется совпадению начальных букв одного и того же числа, записанного на двух различных языках (а несовпадение уподобляется несовпадению). Вероятность совпадения равна ¹/₂₆.

II. Совпадение начальных букв одного и того же числа, записанного да двух разных языках, снова уподобляется совпадению двух букв, одновременно вытащенных из двух различных мешков, и снова оба мешка наполняются, как и раньше, шарами, помеченными буквами. Однако теперь каждый мешок содержит по 100 шаров и каждая буква алфавита используется для пометки стольких различных шаров в мешке, сколько в табл. III имеется наименований чисел, начинающихся с этой буквы. Вероятность совпадений найдена равной 0,0948.

При обеих гипотезах сравнение наименований десяти первых чисел уподобляется десяти независимым вытаскиваниям одной и той же природы.

Мы можем сравнить обе гипотезы с наблюдениями, если вычислим соответствующие вероятности. Нужный материал содержат табл. V и VI.

Таблица V

Абсолютные и относительные частоты и вероятности для n или более совпадений начальных букв[170]

n	Частоты				Вероятности
(1)	10 языков		9 яз. с венг.		Гип. II	Гип. I
	(2)	(3)	(4)	(5)	(6)	(7)
0	45	1,000	9	1,000	1,000000	1,000000
1	40	0,889	5	0,556	0,630644	0,324436
2	35	0,778	3	0,333	0,243824	0,054210
3	31	0,689	0	0,000	0,061524	0,005569
4	25	0,556	0	0,000	0,010612	0,000381
5	15	0,333	0	0,000	0,001281	0,000018
6	9	0,200	0	0,000	0,000108	0,000001
7	7	0,156	0	0,000	0,000006	0,000000

Таблица V сравнивает фактически найденные относительные частоты с вычисленными вероятности. Столбцы (2) и (3) табл V относятся ко всем 45 парам языков, рассмотренных в табл IV. Столбцы (4) и (5) табл. V относятся только к девяти парам, образованным венгерским языком с остальными девятью языками. Для конкретности сосредоточим свое внимание на строке, имеющей дело с 6 или более совпадениями (n = 6). Такие совпадения случаются, как показывает столбец (2), в 9 случаях из 45. Поэтому наблюдаемая относительная частота 6 или более совпадений равна ⁹/₄₅ = 0,2, тогда как шансов на такое число совпадений немногим более, чем

319

Таблица IV

Общее число совпадений, наблюдаемых и теоретических

(Гипотеза II)

	Совпадения		Отклонения
	Наблюдаемые	Ожидаемые	Фактические	Стандартные
10 языков	171	42,66	128,34	7,60
9 яз с венг.	8	8,53	— 0,53	2,78

Один на десять тысяч по гипотезе II и только один шанс на миллион по гипотезе I; см., соответственно, столбцы (6) и (7). Подобные же замечания относятся и к другим столбцам табл. V: то, что фактически наблюдается, по любой из гипотез кажется крайне невероятным, так что имеются серьезные основания отвергнуть обе гипотезы. Однако столбцы (4) и (5) представляют иную картину: наблюдаемые совпадения являются несколько невероятными по гипотезе I, но они кажутся совсем обычными и нормальными с точки зрения гипотезы II. Впечатление, получаемое из табл. V, подкрепляется табл. VI. Если мы рассмотрим все 45 пар языков, то фактически наблюдаемое общее число совпадений резко превышает число совпадений, которое мы должны ожидать на основании гипотезы II, однако ожидаемые и наблюдаемые числа находятся в тесном согласии, если мы рассматриваем только 9 пар, в которые венгерский язык входит вместе с 9 другими языками. (По гипотезе I в обоих случаях мы имеем значительно более сильное расхождение.)

Короче говоря, нет никакой очевидной интерпретации «случайности», которая позволила бы нам объяснить случайностью все совпадения, наблюдаемые в табл. III; их там слишком много. Однако мы вполне разумно можем объяснить случайностью совпадения между венгерским и другими языками. Таким образом, оправдано объяснение, гласящее, что венгерский язык не связан с указанными языками, которые все связаны между собой.

Главное здесь то, что это объяснение было оправдано рассмотрением вероятностей с помощью такого небольшого числа наблюдений.

Главное здесь то, что это объяснение было оправдано рассмотрением вероятностей с помощью такого небольшого числа наблюдений. Само по себе оно подкрепляется подавляющим множеством филологических доказательств.

(5) Из соответствующих наблюдений (с телескопом и спектроскопом) мы можем заключить, что некоторые элементы, найденные в коре земного шара, представлены также в Солнце и некоторых других звездах. Это заключение основано на физическом законе, открытом Г. Кирхгофом почти сто лет назад (этот закон в общих чертах говорит о том, что светящиеся пары поглощают в точности те же лучи света, которые они испускают). Однако в этом заключении известную роль играют вероятности, а именно на этом пункте

320

мы здесь и остановимся; физическую часть рассуждения мы сведем к схематическому наброску.

Пользуясь подходящим прибором (призмой или дифракционной решеткой)¸ мы можем обнаружить в излучении Солнца (в солнечном спектре) некоторую последовательность линий. Мы можем обнаружить последовательность линий также и в излучении, испускаемом некоторыми веществами, например железом, превращенным при высокой температуре в лаборатории в пар. (Фактически линии в спектре Солнца, фраунгоферовы линии, темные, а линии в спектре железа светлые.) Кирхгоф исследовал 60 линий железа и нашел, что каждая из этих линий совпадает с какой-нибудь солнечной линией. (См. грубо схематический рис 14.5.) Эти совпадения вполне понятны, если мы допустим, что на Солнце имеется железо. (Точнее, эти совпадения вытекают из закона Кирхгофа об излучении и поглощении, если мы допустим, что в атмосфере Солнца имеются пары железа, которые поглощают часть световых лучей, испускаемых центральной частью Солнца, раскаленной до некоторой еще более высокой температуры.) Однако, возможно (вот снова неизменное возражение), эти совпадения вызываются случайностью.

Рис. 14.5. Совпадения.

Это возражение заслуживает серьезного рассмотрения. В самом деле,никакое физическое наблюдение не является абсолютно точным. Две линии, которые мы рассматриваем как совпадающие, могли бы в действительности быть различными и только случайно столь близкими одна к другой, что в пределах точности наших наблюдений нам не удалось обнаружить их различия. Мы должны признать, что любое полученное из наблюдений совпадение может быть только кажущимся совпадением, а фактически может иметься небольшое различие. Однако зададим вопрос: вероятно ли, чтобы каждое из 60 наблюдаемых совпадений имело причиной случайное различие, столь малое, что его не удалось обнаружить применяемыми средствами наблюдения?

Кирхгоф, отметивший наблюденные линии на (произвольной) сантиметровой шкале, оценил доступную ему точность, заметив, что он не мог бы не обнаружить различия, превосходящего ½ миллиметра на своей шкале. На этой шкале среднее расстояние между двумя соседними линиями солнечного спектра приблизительно рав-

321

нялась двум миллиметрам. Если бы 60 линий железа были проведены на этом чертеже наугад независимо одна от другой, то какова была бы вероятность того, что каждая из них окажется ближе, чем на ½ миллиметра к какой-нибудь солнечной линии?

Мы приблизим этот вопрос к решению, сформулировав равносильный вопрос в более знакомой области. На полу проведены параллельные прямые; среднее расстояние между двумя соседними прямыми равно 2 см. Мы бросаем монету на пол 60 раз. Если диаметр монеты равен 1 см, то какова вероятность того, что монета каждый раз накроет какую-нибудь прямую?

Рис. 14.6. Равноотстоящие прямые.

В этой последней формулировке на вопрос легко ответить. Допустим сначала, что прямые на полу являются равноотстоящими (как на рис. 14.6.), так что расстояние от каждой прямой до соседней равно 2 см. Если монета накроет прямую, то центр монеты будет находиться самое большее на расстоянии ½ см от этой прямой, и потому он будет лежать где-то в полосе (заштрихованной на рис 14.6) ширины 1 см., которая делится этой прямой пополам. Очевидно, вероятность того, что монета, брошенная на пол 60 раз, каждый раз накроет какую-нибудь прямую, равна (½)⁶⁰.

Допустим теперь, что прямые на полу не являются равноотстоящими; среднее расстояние между двумя соседними прямыми все еще предполагается равным 2 см. Представим себе, что мы переместили в их теперешнее положение прямые, которые первоначально были равноотстоящими, последовательно одну за другой. Если прямая (как прямая b на рис. 14.7) перемещается так, что ее расстояние от ближайшей соседней прямой остается больше чем 1 см, то вероятность для монеты накрыть какую-либо прямую остается неизменной. Если, однако, прямая перемещается таким образом (как прямая d на рис. 14.7), что ее расстояние от соседней прямой становится меньше, чем 1 см., то две (заштрихованные) полосы перекрываются и вероятность для монеты накрыть прямую уменьшается. Поэтому искомая вероятность меньше, чем (½)⁶⁰.

Подведем итоги: если бы линии железа были проведены на солнечном спектре по слепой случайности, то вероятность 60

322

совпадений, наблюдавшихся Кирхгоформ была бы меньше, чем 2^-60 и, значит, меньше, чем 10^-18‑, или

«Эта вероятность, — говорит Кирхгоф, которого мы уже цитировали в эпиграфе к этой главе, — представляется мне еще меньшей из-за того факта, что чем ярче видна данная линия железа, тем темнее, как правило, кажется соответствующая солнечная линия. Следовательно, это совпадение должно быть произведено какой-то причиной, и может быть определена причина, дающая совершенное объяснение полученных из наблюдения фактов».

Рис. 14.7. Прямые на неодинаковых расстояниях.

(6) Следующий пример не основан на действительном наблюдении, но иллюстрирует часто возникающую типичную важную ситуацию.

Крайне опасная болезнь лечится в одной и той же местности двумя различными методами, которые мы будем различать как «старый метод лечения» и «новый метод лечения». Из 9 пациентов, к которым был применен старый метод, 6 умерли и только 3 остались в живых, тогда как из 11 пациентов, лечившихся по новому методу умерли только 2, а остались в живых 9. эти двадцать случаев ясно показаны в табл. VII.

Таблица VII

Корреляционная таблица

Пациенты	Умерли	Остались в живых	Всего
Старый метод	6	3	9
Новый метод	2	9	11
Всего	8	12	20

Первый взгляд на эту таблицу может произвести впечатление, что записанные наблюдения убедительно говорят в пользу нового

323

метода относительная частота смертных случаев равна

⁶/₉, или 67% при старом методе лечения,

²/₁₁, или 18% при новом методе лечения.

Однако, немного подумав, мы можем усомниться, достаточно ли велики полученные из наблюдений числа, чтобы дать нам разумную степень уверенности в только что вычисленных процентах, 67% и 18%. Как бы то ни было, остается фактом, что число смертных случаев при новом методе лечения было намного ниже. Такая низкая смертность могла бы, однако, объясняться случайностью. Насколько легко случайность может вызвать такой результат?

Последний вопрос кажется правильны, но, во всяком случае, этот вопрос, прежде чем на него можно будет дать ответ, должен быть поставлен более точно. Мы должны объяснить точное значение, в котором мы пользуемся словами «случайность» и «такой». Слово «случайность» будет объяснено, если мы уподобим настоящий случай какой-нибудь подходящей азартной игре. Хорошая интерпретация слов «такой результат», по-видимому, гласит: мы рассматриваем все исходы, в которых число смертных случаев при втором методе лечения не выше, чем действительно наблюдавшееся. Таким образом, мы можем прийти в конечном счете к следующей формулировке:

Имеются два игрока, м-р Старый и м-р Новый, и 20 карт, из которых 8 являются черными, а 12 — красными. Карты раздаются таким образом, что м-р Старый получает 9 карт, а м-р Новый получит 2 или менее черные карты?

Эта формулировка насколько возможно просто и отчетливо выражает вопрос, который мы должны исследовать: гипотезу, состоящую в том, что различие между старым и новым методом не является реальным фактом, не имеет реального влияния на смертность, а наблюдавшийся исход был вызван простой случайностью.

Искомая вероятность оказывается равной

Иными словами, исход, кажущийся столь же благоприятным для нового метода лечения, как и наблюдавшийся исход, или даже более благоприятным (поскольку допускаются и случаи с 0 или 1 смертными исходами), будет случайно получен приблизительно один раз из 25 испытаний. И такие числовые доводы в пользу превосходства нового метода лечения над старым не могут быть отклонены, но, разумеется, не являются очень сильными.

Чтобы ясно разобраться в этом вопросе, перейдем на минуту к ситуации, в которой числовые данные привели бы нас к вероят-

324

ности 1/10 000 вместо 1/25. При таких данных было бы очень трудно поверить, что наблюдаемое различие в смертности вызывается простой случайностью, но, конечно, и они еще сразу не доказали бы превосходства нового метода лечения. Эти данные представляли бы очень сильный аргумент в пользу существования какого-то неслучайного различия между течением болезни в этих двух случаях. Какова действительная природа этого различия, эти числа сказать не могут. Если по новому методу лечились только молодые и сильные люди, а по старому только старые и немощные, то аргумент в пользу медицинского превосходства одного метода лечения над другим был бы крайне слабым.

(7) Я думаю, что читатель наметил некоторый параллелизм между шестью предыдущими примерами этого параграфа. Теперь этот параллелизм, пожалуй, созрел для того, чтобы вывести его на чистую воду и сформулировать в общих терминах. Однако будем лучше, насколько это возможно, следовать примеру натуралиста, тщательно сравнивающего относящиеся к делу детали, чем примеру тех философов, которые главным образом полагаются на слова. При рассмотрении наших примеров мы вдавались в множество деталей; если мы тщательно не учтем эти относящиеся к делу подробности, наш труд потерян.

В каждом примере имеются совпадение и объяснение. (Фамилия, имя, занятие и город, где он живет, человека, которого я встретил, совпадает с фамилией, именем, занятием и городом, где он живет, человека, о котором я слышал. Объяснение: эти два человека тождественны. — Два числа, которые вспомнили или вычислили два различных человека, совпадают. Объяснение: число, к которому, работая независимо, пришли два человека, правильно. — Начальные буквы нескольких пар слов, обозначающих на двух различных языках одно и то же число, совпадают. Объяснение: эти два языка связаны. — Светлые линии в спектре железа, наблюдаемые при лабораторном эксперименте, совпадают с некоторыми темными линиями солнечного спектра. Объяснение: в атмосфере Солнца имеются пары железа. — Новый метод лечения болезни совпадает с более низкой смертностью. Объяснение: новый метод лечения более эффективен.)

В противоположность этим специфическим объяснениям, характер которых изменяется вместе с изменением характера примера, существует иное объяснение, которое во всех примерах можно сформулировать в одних и тех же выражениях: наблюдаемые совпадения вызваны случайностью.

Специфические объяснения небезосновательны, некоторые из них разумно убедительны, но ни одно из них не является логически необходимым или строго доказанным. Поэтому ситуация в каждом примере в сущности одинакова[171]: имеются два соперничающих предположения, специфическое предположение и «универсально применимая гипотеза «случайности», приписывающая совпадения случаю.

325

Однако, если мы взглянем на «гипотезу случайности» более пристально, то мы поймем, что эта гипотеза неясна. Утверждение «этот эффект вызван случайностью» неопределенно, так как случай может действовать в соответствии с различными схемами. Если мы желаем получить из этого утверждения какое-нибудь более определенное указание, то мы должны сделать гипотезу случайности более точной, более конкретной; короче, мы должны возвести ее в ранг статистической гипотезы.

В повседневных делах мы обычно не тратим усилий, чтобы с точностью высказать статистическую гипотезу или вычислить ее правдоподобие. Все же мы можем сделать первый шаг в этом направлении [как в примере (1)] или пойти даже немножко дальше [как в примерах (2) или (3)]. В научных вопросах, однако, мы должны ясно формулировать соответствующую статистическую гипотезу и следовать ей вплоть до численной оценки ее правдоподобия, как в примерах (5) и (6).

При переходе от общей и потому несколько расплывчатой идеи случайности к конкретной статистической гипотезе мы должны сделать выбор. Имеются случаи, в которых мы едва ли замечаем этот выбор, так как мы можем придумать лишь одну статистическую гипотезу, достаточно простую и довольно хорошо подходящую к данному случаю; в подобном случае выбранная гипотеза кажется «естественной» [как в примерах (3), (5) и (6)]. В других случаях необходимость выбора нетрудно заметить; мы сразу не видим статистической гипотезы, которая была бы достаточно проста и подходила бы к случаю в какой-то мере «реально»; таким образом, мы после бо́льших или меньших колебаний делаем выбор [как в примере (4)].

В конечном счете имеются два соперничающих предположения, противостоящих одно другом: нестатистическое, скажем, «физическое предположение Ф и статистическая гипотеза С. теперь наблюдалось некоторое событие Е. Это событие Е связано и с Ф, и с С и связано так, что его появление может оказать влияние на наш выбор между двумя соперничающими предположениями Ф и С. Если физическое предположение Ф истинно, то Е кажется легко объяснимым, его появление легко можно понять. В наиболее прозрачных случаях [как в примере (5)] Е вытекает из Ф, является следствием Ф. С другой стороны, с точки зрения статистической гипотезы С событие Е кажется «совпадением», вероятность p которого может быть вычислена на основании гипотезы С. Если вероятность p события Е оказывается низкой, появление события Е не легко объяснить «случайностью», т. е. статистической гипотезой С; это ослабляет нашу уверенность в С и, соответственно, усиливает нашу уверенность в Ф. Наоборот, если вероятность p наблюдавшегося события Е высока, то Е может казаться объяснимым случайностью, т. е. статистической гипотезой С; это несколько усиливает нашу уверенность в С и соответственно ослабляет уверенность в Ф.

326

Следует отметить, что предыдущее находится в согласии с тем, что мы говорили по поводу соперничающих предположений в § 13.12, и несколько уточняет схему правдоподобного рассуждения, рассмотренную в § 12.3.

Вездесущая гипотеза случайности является альтернативой к любому другому виду объяснения. Это, по-видимому, глубоко коренится в человеческой природе. «Нарочно или нечаянно?» «Существует ли определенная причина или это только случайное совпадение?» Какой-то вопрос такого рода приходит в голову почти при каждом обсуждении или обдумывании, в обычной беседе и в судебном заседании, в повседневных делах и в науке.

10. Оценка математических предположений. Сравним некоторые примеры, рассмотренные в предшествующих главах, друг с другом и с примерами, рассмотренными в предыдущем параграфе.

(1) Вспомним историю замечательного открытия, рассказанную в § 2.6. Эйлер исследовал бесконечный ряд

Сначала он нашел различные преобразования этого ряда. Затем, пользуясь одним из этих преобразований, он получил приближенное числовое значение для суммы ряда, значение 1,644934. наконец, с помощью нового и дерзкого приема он догадался, что сумма ряда равна π²/6. Эйлер сам чувствовал, что его прием был дерзким, даже вызывающим возражения, но он имел достаточные основания верить в свое открытие: значение, найденное с помощью числовых выкладок, 1,644934, в тех знаках, которые были вычислены, совпадало с угаданным значением

и Эйлер был уверен. Однако была ли его уверенность разумной? Такое совпадение может быть вызвано случайностью?

Действительно, не вполне невозможно, чтобы такое совпадение было вызвано случайностью; однако имеется один шанс на десять миллионов, чтобы случилось такое совпадение: вероятность того, чтобы такое совпадение семи десятичных знаков произошло по случайности, просто интерпретированной, равна 10^–7; ср. § 9 (3) и пример 11. И поэтому мы не должны порицать Эйлера за то, что он отверг объяснение случайным совпадением и оставался верным своей догадке: π²/6. В конце концов он доказал, что его догадка была верна. Но мы не должны придавать слишком большого значения тому факту, что это было доказано. С доказательством или без доказательства, догадка Эйлера сама по себе является не только блестящей, но и разумной.

327

(2) Взглянем снова на § 3.1. и, в частности, на рис. 3.1., на котором изображены девять многогранников. Для каждого из этих многогранников мы определили числа Г, В, и Р, т. е., соответственно, число граней, вершин и ребер, и найденные числа записали в таблицу (стр. 57). Затем мы подметили закономерность: всюду в таблице

Г + В = Р + 2.

Нам показалось невероятным, чтобы такая упорная закономерность оказалась простым совпадением, и, таким образом, мы пришли к предположению, что наблюдаемое в девяти случаях соотношение является верным вообще.

В этом рассуждении имеется пункт, который можно было бы сделать более точным: какова вероятность такого совпадения? Чтобы ответить на этот вопрос, мы должны предложить определенную статистическую гипотезу. Я не в состоянии придумать гипотезу, полностью подходящую к нашему случаю, но есть гипотеза, имеющая некоторое отношение к этой ситуации. Я выскажу ее, положив Г — 1 = X, В — 1 = Y, P = Z. После этого изменения обозначений предполагаемое соотношение приобретает вид X + Y = Z.

Имеем три мешка, каждый из которых содержит n шаров, занумерованных числами 1, 2, 3, …, n. Мы вытаскиваем по одному шару из каждого мешка, и пусть X, Y и Z, соответственно, обозначают номера шаров из первого, второго и третьего мешка. Какова вероятность того, что мы случайно получим соотношение

X + Y = Z

между этими тремя числами X, Y и Z?

Подразумевается, что три вытаскивания взаимно независимы. При этом условии искомая вероятность вполне определена и мы легко находим, что она равна

Применим это к нашему примеру. Сосредоточим свое внимание на том моменте, когда нам удалось подтвердить гипотетическое соотношение для нового многогранника. Например, после девяти многогранников, которые мы исследовали первоначально (в § 3.1.), мы перешли к случаю икосаэдра (в § 3.2). Для икосаэдра, как мы нашли, Г = 20, В = 12, Р = 30, и, таким образом, действительно,

(Г — 1) + (В — 1) = 19 + 11 = 30 = Р.

Не является ли это простым случайным совпадением? Применим нашу формулу, взяв n = 30 (мы, разумеется, не можем сделать n меньше 30), и найдем, что такое событие имеет вероятность

328

т. е у него несколько ме́ньшие шансы, чем один шанс на 60. Мы можем колебаться, следует ли нам приписать подтверждение предполагаемого соотношения простой случайности или нет. Однако если нам удается убедиться, что оно верно и для другого многогранника с Г, В и Р приблизительно такими же, как для икосаэдра и мы склонны рассматривать эти два подтверждения как независимые, то мы встречаем событие (совместное подтверждение в обоих случаях) с вероятностью меньшей, чем (1/60)²; шансов произойти для этого события меньше, чем 1 шанс из 3600, и поэтому его уже труднее объяснить случайностью. Если подтверждения продолжаются без перерыва, то раньше или позже наступит момент, когда мы почувствуем себя обязанными отвергнуть объяснение случайностью.

(3) В предыдущем примере мы не должны делать особого ударения на полученных нами численных значениях вероятностей. Для руководства нашим суждениям ясное понимание того, что вероятность неуклонно возрастает, когда подтверждение следует за подтверждением, пожалуй, полезнее, нежели найденные числовые значения. Как бы то ни было, существуют случаи, когда было бы трудно предложить подходящую статистическую гипотезу, и, таким образом, невозможно вычислить нужные вероятности, и когда тем не менее исчисление вероятностей все еще дает полезные указания.

В § 4.8 мы сравнили два предположения относительно суммы четырех квадратов. Назовем их соответственно предположением A и предположением B. Предположение A, которое мы открыли в конце § 4.6) выдвигает замечательное правило, точно определяющее, сколькими способами целое число некоторого вида можно представить в виде суммы четырех нечетных квадратов. Предположение B (предположение Баше) утверждает, что любое целое число может быть представлено в виде суммы четырех квадратов одним или более способами. Каждое из этих двух предположений предлагает предсказание в отношении суммы четырех квадратов, но предсказание предлагаемое A, точнее предлагаемого B. Именно для того, чтобы это подчеркнуть, рассмотрим на минуту совершенно неправдоподобное допущение. Допустим, что из какого-то (таинственного источника мы знаем, что в известном случае число представлений имеет равные шансы принять любое из r + 1 значений 0, 1, 2, …, r и не может принять значения[172], превосходящего, превосходящего r, которое является очень большим числом (и это должно иметь место и при условиях, требуемых в A, и при условиях, требуемых в B, — довольно нелепое допущение). И вот A предсказывает, что это число больше нуля. Поэтому вероятность того, что при этом допущении окажется верным A, равна 1/(r + 1), тогда как вероятность того, что окажется верным B, равна r/(r + 1). В действительности и A, и B в этом случае оказываются верными ; оба предположения подтверждаются, и возникает вопрос, какое подтверждение дает более убедительные

329

доводы? Ввиду того, что мы только что сказали, значительно труднее приписать случайности подтверждение A, чем подтверждение B. Благодаря этому обстоятельству (в согласии со всеми подобными же примерами, рассмотренными в этой главе) подтверждение более точного предсказания A должно иметь больше веса, чем подтверждение менее точного предсказания B. В § 4.8 мы пришли к тому же мнению, в явной форме не рассматривая вероятностей.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ XIV

Первая часть

Каждый пример в этой первой части начинается со ссылки на какой-нибудь параграф или пункт этой главы и дает формулы или выводы, опущенные в тексте. Решения требуют некоторого знания исчисления вероятностей.

1 [§ 3 (3)]. Примите схему § 3 (3) для представления последовательности дождливых и недождливых дней. Будем для удобства говорить «солнечный» вместо «недождливый» и пусть r_r, s_r, r_s, s_s[173] обозначают вероятности:

r_r — дождливого дня после дождливого дня?

s_r — солнечного дня после дождливого дня,

r_s — дождливого дня после солнечного дня и

s_s — солнечного дня после солнечного дня.

(a) Докажите, что r_r — r_s = s_s — s_r.

(b) Было сказано, что за «дождливым днем охотнее, чем недождливый¸ следует дождливый день». Каково значение этих слов?

2 [§ 3 (4)]. Было сказано, что «каждая буква стремится быть непохожей на предыдущую букву». Каково точное значение этих слов?

3 [§ 5 (1)]. Найдите общее выражение для чисел в столбце (3) табл. I.

4 [§ 5 (2)]. Найдите общее выражение для чисел в столбце (5) табл. I.

5 [5 (3)]. (a) Найдите общее выражение для чисел в столбце (3) табл. II. (b) Чтобы обнаружить систематическое отклонение, если оно имеется, исследуйте разности соответствующих чисел (в одной и той же строке) столбцов (4) и (5); запишите знаки.

6 [§ 7 (1)]. Если испытание состоит в бросании трех честных игральных костей и успех состоит в выпадении шести очков на каждой кости, то какова вероятность n успехов при n испытаниях?

7 [§ 7 (2)]. Какое из различных событий, сообщенных в истории преподобного Галиани, которая была рассказана в § 7 (1), дает наиболее сильный аргумент против гипотезы честных костей?

8 [§ 7 (2)]. (a) Напишите формулу, приводящую к числовому значению 1,983·10^–7.

(b) Вероятность успеха равна ⅓. Найдите вероятность того, что 315 672 испытания дадут точно 315 672/3 успеха.

9 [§ 8 (1)]. Выражение, приведенное для a представляет собою сумму. Каждый член этой суммы на самом деле является вероятностью: чего?

10 [§ 8 (1)]. Найдите абсциссу точки перегиба кривой, изображенной на рис. 14.4.

11 [§ 9 (3)]. Дано n-значное число. Последовательность n цифр задается случайно, быть может, обезьяной, играющей клавишами счетной машины. Какова вероятность того, что так полученная последовательность совпадет с данным числом? [Является ли ответ математически определенным?]

12 [§ 9 (4)]. Объясните вычисление вероятности 0,0948.

13 [§ 9 (4)]. Найдите общее выражение для чисел (а) в столбце (6), (b) в столбце (7) табл. V.

14 [§ 9 (4)]. Объясните вычисление ожидаемых чисел совпадений в табл. VI: (a) 42, 66, (b) 8,53.

330

15 [§ 9 (4)]. Объясните вычисление стандартного отклонения 2,78 в последней строке и последнем столбце табл. VI.

16 [§ 9 (5)]. Почему (1/2)⁶⁰?

17 [§ 9 (6)]. Объясните вычисление вероятности 0,399. [Обобщите.]

18 [§ 9 (6)]. Выведите выражение (n — 1)/2n² для искомой вероятности.

Вторая часть

19. О понятии вероятности. Параграф 2 не определяет, «что такое» вероятность, а пытается только объяснить, что вероятность стремится описать: относительную частоту «дальнего действия», «окончательную устойчивую» относительную частоту, или относительную частоту в «очень длинном ряде наблюдений[174]. Насколько такой ряд предполагается длинным, не говорилось. Это упущение.

Однако такие упущения в науке нередки[175]. Возьмем наиболее старую физическую науку, механику, и определение скорости неравномерного прямолинейного движения: скорость есть путь, описываемый движущейся точкой за некоторый промежуток времени, деленный на длину этого промежутка, при условии, что этот промежуток «очень мал». насколько малым предполагается такой промежуток, не говорится.

Практически, вы берете измеренный промежуток времени настолько коротким или наблюденный статистический ряд настолько длинным, насколько вам позволяют средства наблюдения. Теоретически, вы можете перейти к пределу. Физик при определении скорости заставляет промежуток времени стремиться к бесконечности[133]).

20. Как не следует истолковывать понятие вероятности, основанное на частоте. Д-р Тел покачал головой, когда закончил исследование пациента. (Д-р Тел означает доктор телепатии; несмотря на энергичное противодействие медицинских работников, практика телепатии была законно признана в пятьдесят третьем штате США[134].[176] «У вас очень серьезная болезнь, — сказал д-р Тел. — Из десяти человек, заболевших ею, выживает только один». Когда пациент был достаточно напуган этим сообщением, д-р Тел продолжал: «Но вы счастливчик. Вы останетесь живы, потому что вы обратились ко мне. У меня уже было девять пациентов, и все они умерли от этой болезни».

Возможно, д-р Тел так и думал. Его дед был матросом, корабль которого был поражен в морском бою снарядом. Матрос засунул свою голову в дыру, проделанную снарядом в корпусе корабля, и чувствовал себя в безопасности, «потому что, — рассуждал он, — очень невероятно[177], чтобы снаряд попал в одно и то же место дважды».

21. Чиновник, которому было поручено наблюдать за выборами в определенной местности, нашел 30 фальшивых регистраций среди 38, которые он проверил в первое утро. Ежедневная газета утверждает, что по крайней мере 99% регистраций в этой местности правильны и выше подозрений. Как должно выглядеть это утверждение газеты в свете наблюдения чиновника?

22. В окне лавки часового мастера выставлено четверо часов с кукушкой, причем все они идут. Трое из этих часов расходятся меньше чем на две минуты: можете ли вы положиться на время, которое они показывают? Имеется естественное предположение: часы первоначально были поставлены правильно, но они не очень точны (они ведь часы с кукушкой), а одни часы не в порядке. Если этот так, то вы можете положиться на время, показываемое тремя часами. Однако

331

существует, конечно, соперничающее предположение: эти трое часов находятся в согласии просто случайно. Какова вероятность такого события?

23. Если a, b, c, d, e и f — выбранные наугад целые числа, не превосходящие по абсолютной величине данного положительного целого числа n, то какова вероятность того, что система

ax + bx = e,

cx + , dx = ef

двух уравнений с двумя неизвестными имеет только одно решение?

24. Вероятность и решение задач. В кроссворде одно неизвестное слово из 5 букв пересекается с двумя неизвестными словами, каждое из которых состоит из четырех букв.

Вы догадываетесь, что неизвестное пятибуквенное слово ВЫШКА, и после этого имеете ситуацию, указанную на приведенной диаграмме. Чтобы проверить вашу догадку, вам хотелось бы найти то или другое четырехбуквенное слово, пересекающее предполагаемую ВЫШКУ. Одно из пересекающих слов могло бы подтвердить Ы, другое — К. Какое подтверждение имело бы больший вес? И почему?

25.

I	II
1005	1004
1033	1038
1075	1072
1106	1106
1132	1139
1179	1173
1205	1206
1231	1239
1274	1271
1301	1303

Один из столбцов «правильный», а другой «неправильный». Правильный столбец содержит десять последовательных мантисс четырехзначной таблицы десятичных логарифмов. Числа неправильного столбца в первых трех знаках совпадают с соответствующими числами правильного столбца, но четвертые знаки могли бы быть результатом работы ненадежного вычислителя: они были выбраны «наугад». Который столбец является каким? [Укажите регулярный прием, позволяющий отличить правильный столбец от неправильного.]

26. Фундаментальные правила исчисления вероятностей. При вычислении вероятностей мы можем ясно себе представить совокупность возможных случаев и интуитивно увидеть, что ни один из них не является привилегированным, или же мы можем действовать в соответствии с правилами. Для начинающего важно ясно понять, что к одному и тому же результату мы можем прийти этими двумя различными путями. Правила практически важны, когда мы рассматриваем теорию вероятностей как чисто математическую теорию. Эти правила будут играть важную роль в следующей главе. По всем этим причинам мы введем здесь фундаментальные правила исчисления вероятностей, пользуясь мешками и шарами[135]; ср. § 3.[178]

332

Мешок содержит p шаров. Некоторые из шаров помечены буквой A, другие — буквой B, некоторые обеими буквами и некоторые не помечены вовсе. (Имеется p возможных случаев и два «свойства», или «события» A и B.) Символом Ā будем обозначать отсутствие A, или «не-A». (Мы берем «͞ » в качестве знака отрицания, но помещаем этот знак не перед буквой, а над ней.) имеются четыре возможности, четыре категории шаров.

Шар с A, но без B. Обозначим эту категорию символом A^͞B, а число таких шаров — буквой a.

Шар с B, но без A. Обозначим эту категорию символом ĀB, а число таких шаров — буквой b.

Шар и с A, и с B. Обозначим эту категорию символом AB, а число таких шаров — буквой c.

Шар без A, и без B. Обозначим эту категорию символом Ā^͞B, а число таких шаров — буквой d.

Таким образом, очевидно,

a + b + c + d = p.

Пусть P{A} сокращенно обозначает вероятность A, а P{B} — вероятность B. При таких обозначениях, очевидно, имеем

Пусть P{AB} сокращенно обозначает «вероятность A и B», т. е. вероятность совместного появления A и B. Очевидно,

Пусть P{A или B} обозначает вероятность появления A или B или и A, и B[136][179]. Очевидно,

Легко видеть, что

P{A} + P{B} = P{AB}+ P{A или B},

и отсюда следует наше первое фундаментальное правило (правило «или»):

P{A или B} = P{A} + P{B} — P{AB}. (1)

Мы хотим теперь определить условную вероятность P{A/B} словами: вероятность A, если B, (допуская B, при условии B, при гипотезе B, …). И эта вероятность предназначена для представления относительной частоты дальнего действия. Мы вытаскиваем шары из мешка раз за разом, каждый раз

333

по одному шару, возвращая вытащенный шар перед тем, как вытащить следующий, как это подробно описано в §2 (1). Однако мы принимаем в расчет только шары с B. Если среди первых n таких вытащенных шаров имеется m шаров, помеченных также A, то m/ n есть относительная частота, которая, когда n достаточно велико, должна приближенно равняться P{A/B}. Кажется довольно очевидным[180], что

Действительно, среди b + шаров с B имеется c шаров с A; можно повторить и рассуждение из §2 (1); с известной точки зрения мы могли бы в качестве определения рассматривать и указанное выражение P{A/B}. Как бы то ни было, сравнивая выражения входящих сюда вероятностей, легко находим, что

P{A/B} = P{A/B}/P{B}.

Меняя местами A и B, находим второе фундаментальное правило (правило «и»)

P{AB} = P{A}P{B/A} = P{B}P{A/B}. (2)

Из (1) и (2) мы можем вывести много других правил. Замечая, что

P{A или Ā} = 1, P{AĀ} = 0

из (1) получаем, подставляя Ā вместо B,

P{A} + P{Ā} = 1,

что мы, конечно, могли бы увидеть и непосредственно. Подобным же образом, так как

P{AB или ĀB} = P{B}, P{(AB)(ĀB)} = 0,

из (1) получаем, подставляя AB вместо A и ĀB вместо B,

P{B} = P{AB} + P{ĀB}.

Отметим здесь следующее обобщение (2):

P{AB/H} = P{A/H}P{B/HA} = P{B/A} P{A/HB}.

Мы можем также ясно увидеть (5), пользуясь мешком и шарами.

27. Независимость. Мы называем два события независимыми друг от друга, если наступление (или ненаступление) одного из них не оказывает никакого влияния на шансы другого. Оставим, однако, на время это неформальное определение и рассмотрим два следующих формальных определения:

(1) A называется независимым от B, если

P{A/B} = P{A/^͞B} = P{A}, P{B/A} = P{B/Ā} = P{B}.

Очевидно, если A и B взаимно независимы, то A независимо[181] от B. пользуясь правилами примера 26, докажите теорему: Если ни одна из вероятностей P{A}, P{B}, P{Ā}, P{^͞B} не равна нулю и если любое из двух событий A и B не зависимо[182] одно от другого, то они взаимно независимы.

28. Сравните § 3(5) с примером 27.

29. Машина¸ следующая из города M в город N, может проехать через город A, а также через город B. Это верно для обеих систем дорог (I) и (II), изобра-

334

женных на рис. 14.8. Ответьте на следующие вопросы (a), (b) и (c) сначала в предположении, что полную систему дорого между M и N изображает (1), а затем в таком же предположении относительно (II).

Системы дорог из города M в город N с существенным различием.

(a) Пусть A обозначает событие, состоящее в том, что машина, следующая из M в N, проезжает через город A, а B — событие, состоящее в том, что она проезжает через B. Допустите [ для обеих систем (I) и (II)], что тремя дорогами, начинающимися в M, пользуются одинаково часто (с одинаковой вероятностью), а также что одинаково часто пользуются дорогами, оканчивающимися в N [их 2 в (I) и 6 в (II)]. Найдите вероятности P{A}, P{A/B}, P{A/^͞B} P{B}, P{B/A}, P{B/Ā}.

(b) Найдите P{A/B}, пользуясь правилом (2) примера 26.

(c) Проверьте, что

P{A} = P{B}P{A/B} + P{^͞B}P{A/^͞B},

P{B} = P{A}P{B/A} + P{Ā}P{B/Ā}.

(d) Что вы рассматриваете как наиболее важное различие между (I) и (II)?

30. Перестановки и вероятность. Чтобы определить порядок, в котором должны показать свое мастерство n участников спортивного состязания, фамилия каждого из них записывается на листке бумаги и затем n листков вытаскиваются из шапки один за другим, случайно. Какова вероятность, что n фамилий появятся в алфавитном порядке.

Мы изложим два решения и выведем из их сравнения заключение.

(1) Пусть E₁ — событие, состоящее в том, что листок, вытащенный первым, является и первым по алфавиту, E₂ — событие, состоящее в том, что листок, вытащенный вторым, является и вторым по алфавиту и т. д. Искомая вероятность равна

Действительно, первое преобразование мы получаем, применяя правила (2) и (5) примера 26, а второе преобразование, подмечая, что для E₁ имеется n возможных случаев, для E₂ после E₁ — (n — 1) случаев, для E₃ после E₁ и E₂ — (n — 2) случаев и т. д., тогда как для каждого из этих событий имеется только один благоприятствующий случай.

(2) Пусть P_n — число всех возможных расположений (перестановок, линейных упорядочений, …) n различных предметов. Тогда n фамилий могут быть вытащены из шапки P_n способами, ни один из этих P_n случаев, по-видимому, не имеет преимущества по сравнению с другими и среди этих P_n

335

случаев только один (алфавитный порядок) является благоприятствующим. Следовательно, искомая вероятность равна 1/ P_n.

(3) Результаты, выведенные в (1) и (2), должны быть одинаковы. Сравнивая их, находим P_n:

P_n = 1·2·3 … n = n1.

31. Сочетания и вероятность. М-с Смит купила n яиц, не зная, что r из этих яиц тухлые. Ей нужны r яиц, она выбирает их из своих n яиц наугад. Какова вероятность того, что все r яиц окажутся тухлыми?

Как и в примере 30, мы изложим два решения, и из их сравнения выведем заключение.

(1) Пусть E₁ — событие, состоящее в том, что первое разбитое м-с Смит яйцо оказалось тухлым, E₂ — событие, состоящее в том, что второе яйцо оказалось тухлым, и т. д. Искомая вероятность равна

Первое преобразование получается по правилам (2) и (5) примера 26, второе — из рассмотрения возможных и благоприятствующих случаев для E₁, для E₂ после E₁ и т. д.

(2) Имеем множество из n различных предметов. Любые r предметов, выбранных среди этих n предметов, образуют подмножество мощности r данного множества мощности n; обозначим через C′ число всех таких подмножеств. (Обычно C′_n называется числом «сочетаний» из n элементов по r). В случае яиц м-с Смит имеется C′_n возможных случаев, ни один из которых не имеет преимуществ по сравнению с другими, и среди этих C′_n случаев только один благоприятствующий (если получение тухлых яиц можно называть «благоприятствующим»[183]). Следовательно, искомая вероятность равна 1/C′_n.

(3) Сравнивая (1) и (2), находим C′_n:

32. Выбор соперничающего статистического предположения. Пример. Один человек взял в определенный день 875 долларов со своего сберегательного счета, а другой человек двумя днями позже получил 875 долларов. Совпадение этих двух сумм, одной взятой, а другой полученной, может рассматриваться как косвенная улика, как указание, что было совершено преступление; ср. пример 13.6. Если присяжные найдут слишком трудным поверить, что это совпадение вызвано простой случайностью, то результатом может быть осуждение[184]. Отсюда задача: какова вероятность такого совпадения? Чем меньше вероятность, тем труднее приписать совпадение случайности и тем сильнее улики против обвиняемых[185].

Однако мы не можем вычислить вероятность, не принимая какой-либо определенной статистической гипотезы. Какую гипотезу следовало бы нам принять? В серьезном случае нам следует высказать по подобному вопросу серьезные соображения. Рассмотрим несколько возможностей.

(1) Поскольку число 875 состоит из трех цифр, мы можем рассматривать в качестве допустимых положительные целые числа, состоящие не более чем из трех чисел, и можем считать их равновозможными. Вероятность того, что два таких числа, выбранных наугад независимо друг от друга, совпадут, очевидно, равна 1/999. Эта вероятность довольно мала, но разумно ли допущение, на котором основано ее вычисление?

336

(2) Поскольку 875 состоит меньше чем из пяти цифр, мы могли бы рассматривать в качестве допустимых и равновозможных все положительные целые числа, состоящие из менее чем пяти цифр. Это приводит к вероятности совпадения 1/9999. Эта вероятность в самом деле очень мала, но наше допущение притянуто за волосы, даже несерьезно.

(3) Если вопрос представляется важным, суд может назначить проверку банковских книг или вызвать в качестве свидетеля одного из компетентных служащих банка. Пусть таким путем было установлено, что непосредственно перед тем как со счета была взята сумма 875 долларов, на счете находилась сумма 2581 доллар 48 центов. Владея этой существенной информацией, мы можем рассматривать в качестве допустимых и равновозможных случаев суммы 1, 2, 3, …, 2581, которые могли бы взять со счета. Лишь один из этих случаев, 875, должен быть назван благоприятствующим, и таким образом мы приходим к вероятности совпадения 1/2581. Это — небольшая вероятность, но наше допущение может казаться довольно реалистичным.

(4) Мы могли бы рассматривать не только суммы в долларах, но и суммы в долларах и центах, как, например, 875 долларов 31 цент. Если мы будем рассматривать как равновозможные все такие случаи, то вероятность совпадения станет равной 1/258248. Это — очень маленькая вероятность, но наше допущение может казаться менее реалистичным: суммы в долларах и центах, как, например, 875 долларов 31 цент, обычно берут с чекового счета, а не со сберегательного.

(5) Напротив, кто-нибудь мог бы убеждать нас, что суммы, взятые со сберегательного счета, обычно бывают «круглыми» суммами, делящимися на 100, или на 50, или на 25. Ну вот, 875 делится на 25. если мы рассмотрим в качестве допустимых и равновозможных только суммы, кратные 25, то наша вероятность станет равной 1/103.

Конечно, мы могли бы вообразить и другие, более сложные, способы вычисления этой вероятности, но нам нет необходимости слишком долго останавливаться понапрасну на таком прозрачном примере[186]. Этот пример послужил своей цели, если читатель может теперь осознать следующие два обстоятельства:

(a) Хотя некоторые из пяти обсуждавшихся допущений могут казаться более приемлемыми, чем другие, ни одно из них не является явно превосходящим другие и мало надежды найти допущение, которое было бы во всех отношениях удовлетворительным и могло бы рассматриваться как наилучшее.

(b) Каждое из пяти рассмотренных допущений приписывает фактически наблюдавшемуся совпадению довольно малую вероятность и, таким образом, наше рассмотрение поддерживает точку зрения, основанную на здравом смысле: трудно поверить, что это совпадение вызвано простой случайностью»[187].

33. Выбор соперничающего статистического предположения. Общие замечания. Попытаемся на рассмотренном частном примере (пример 32) научиться кое-чему более общему. Вновь рассмотрим общую ситуацию, которую мы обсуждали в § 14.9 (7). Событие E произошло и наблюдалось. Относительно этого события имеются два соперничающих предположения, противостоящих одно другому: «физическое» предположение Ф и статистическая гипотеза С. Если мы примем физическое предположение Ф, то E можно легко и довольно разумно объяснить. Если мы примем статистическую гипотезу С, то мы сможем вычислить вероятность p того, что произойдет событие E. Если p «мала», то мы можем склониться к тому, чтобы отвергнуть статистическую гипотезу С. Как бы то ни было, малость p ослабляет нашу уверенность в С и, следовательно, несколько усиливает нашу уверенность в соперничающем предположении Ф.

Однако пример 32 заставляет нас осознать, что в описанном рассуждении играет роль качество статистической гипотезы С. Статистическая гипотеза С может казаться неестественной, неподходящей, притянутой за волосы, несерьезной, дешевой, ненадежной с самого начала. Или же С может казаться естественной, подходящей, реалистичной, разумной, сама по себе надежной.

337

Далее, p, вероятность события Е, вычисленная на основании гипотезы С, может быть так мала, что мы отвергаем С: соперница предположения Ф выбывает из состязания. Это повышает шансы предположения Ф, но может их повысить значительно или только немного: это зависит от качества соперницы. Если статистическая гипотеза С первоначально казалась нам подходящей и надежной, то С была опасной соперницей и ее падение ощутимо усиливает Ф. Если, однако, С с самого начала казалась нам неподходящей и ненадежной, то С была слабой соперницей: ее падение неудивительно и усиливает Ф очень мало.

Если дана ясная статистическая гипотеза С, то вероятность p события Е является вполне определенной и статистик может ее вычислить. Однако заказчик статистика, который может быть биологом или психологом или деловым человеком или каким-нибудь другим нестатистиком, должен решить, что в его случае означает это числовое значение p. Он должен решить, насколько малого p достаточно, чтобы отвергнуть или ослабить статистическую гипотезу С. Но заказчик обычно даже не интересуется соперничающим «физическим» предположением Ф. И он должен решить, насколько отказ от гипотезы С или ее ослабление усилит Ф. Это последнее решение, очевидно, не может зависеть от одного лишь числового значения p: оно, конечно, зависит и от выбора С.

Я боюсь, что заказчик статистика, желающий воспользоваться числовым значением p, которое ему дал статистик, без ясного понимания важности статистической гипотезы С для его задачи, просто обманывает себя. Он едва ли сможет понять важность гипотезы С, если ясно не поймет, что его физическому предположению могут быть также противопоставлены и статистические гипотезы, отличные от С. Ср. пример 15.5.

XV. ИСЧИСЛЕНИЕ ВЕРОЯТНОСТЕЙ И ЛОГИКА ПРАВДОПОДОБНЫХ РАССУЖДЕНИЙ

Трудно оценить вероятность результатов индукции. — Лаплас[137]

Мы знаем, что вероятность хорошо установленной индукции велика, но когда нас просят назвать ее степень, мы этого сделать не можем. Здравый смысл говорит нам, что некоторые индуктивные аргументы сильнее, чем другие и что некоторые являются очень сильными. Но насколько сильнее или насколько сильными, выразить мы не можем. — Джон Майнард Кейнс[138]

1. Правила правдоподобных рассуждений. В трех предыдущих главах мы собрали схемы правдоподобных рассуждений. Образуют ли эти «схемы» «правила» правдоподобных рассуждений? Насколько и в каком отношении являются они обязательными, повелительными, императивными? Существует некоторая опасность заблудиться в чисто словесных объяснениях. Поэтому я хочу рассмотреть этот вопрос более конкретно, даже немножко лично.

(1) Я вспоминаю один разговор об изобретении и правдоподобных рассуждениях. Он происходил очень давно. Я беседовал с другом, который был намного старше меня и имел за своей спиной выдающийся перечень открытий, изобретений и успешной профессиональной работы. Когда он говорил о правдоподобных рассуждениях и изобретении, он, несомненно, знал, о чем говорит. С необычайным жаром и силой убеждения он отстаивал тот взгляд, что изобретение и правдоподобные рассуждения не имеют никаких правил. Предчувствия и догадки, говорил он, зависят от опыта и интуиции, но не от правил: нет никаких правил, не может быть никаких правил, не должно быть никаких правил, и если бы существовали какие-нибудь правила, они, во всяком случае, были бы бесполезны. Я защищал противоположный взгляд — разговор был бы неинтересен, если бы не было никакого различия в мнениях, — но я чувствовал силу его позиции. Мой друг был хирургом. Ошибочное решение хирурга может стоить жизни, и иногда, когда больной внезапно начинает истекать кровью или задыхаться, правильное решение должно найтись в секунду. Я понимал, что люди, которые должны принимать такие ответственные быстрые решения, не нуждаются в правилах. Времени слишком мало, чтобы должным образом применить правило, и любая установленная схема могла бы ввести вас в заблуждение; то, что вам

339

нужно, это глубоко сосредоточиться на находящейся перед вами ситуации. И, таким образом, люди начинают недоверять[188] «правилам» и полагаются на свою «интуицию» или на свой «опыт» или на «интуицию и опыт»[189].

В случае моего друга было, возможно, еще нечто другое. Он немножко любил командовать. Он очень не любил[190] уступать власть. Он чувствовал, возможно, что признание правила подобно передаче части его полномочий машине, и потому он был против него[191].

Отметим: недоверие к правилам рассуждений может естественно возникнуть у умных людей.

(2) Два человека, которым представлены одни и те же доводы, могут оценивать их очень различно[192]. Двое присяжных, участвующих в одном и том же процессе, могут быть несогласны[193]: один думает, что представленные доводы являются достаточным доказательством виновности подсудимого, а другой думает, что это не так. Такое несогласие может иметь тысячу различных оснований: людей могут толкать в противоположных направлениях опасения, надежды, предубеждения и симпатии или личные различия[194]. Быть может, один из этих присяжных глупый, а другой умный или один спал на протяжении всего процесса, а другой внимательно слушал. Однако индивидуальные различия, лежащие в основании несогласия, могут быть и более тонкими. Быть может, оба присяжных честны и разумно непредубежены[195], оба внимательно следят за процессом и оба умны, но по-разному. Первый присяжный, возможно, лучше замечает, как ведут себя люди. Он наблюдает за выражением лица свидетелей, за вздрагиваниями подсудимого: он подмечает, когда ответ дается с запинками; в его уме запечатлеваются быстрые движения глаз и небольшие жесты рук. Другой присяжный, возможно, менее искусно наблюдает за выражением лица[196], но лучше оценивает социальные отношения: он лучше понимает среду и условия жизни людей, вовлеченных в процесс. Видя одно и то же разными глазами, честно и не неразумно, двое присяжных приходят к противоположным заключениям.

Не будем игнорировать очевидного и отметим: два человека, которым представлены одни и те же доводы, .могут честно быть несогласны.

(3) Мой друг и я оба интересуемся предположением A. (Этот друг математик, и A — математическое предположение.) Мы оба знаем, что A влечет за собой B. И теперь мы находим, что B, это следствие A, верно. Мы согласны, — как мы честно и должны быть согласны, — что это подтверждение следствия B предположения A является доводом в пользу A, но не согласны в отношении значения, или веса этого довода. Один из нас считает, что это подтверждение очень мало прибавляет к правдоподобности A, а другой, — что оно прибавляет много.

Это несогласие можно было бы понять, если бы мы были очень неодинаково знакомы с предметом и один из нас знал бы значительно

340

больше ранее подтвержденных следствий, чем другой. Но это не так. Мы знаем примерно одни и те же следствия A, подтвержденные ранее. Мы согласны даже, что между только что подтвержденным следствием B и этими ранее подтвержденными следствиями аналогия невелика. Мы согласны также, — как мы честно и должны быть согласны, — что это обстоятельство усиливает указанный довод в пользу A. Но один из нас говорит «лишь немного усиливает», а другой говорит «значительно усиливает», и мы не согласны[197].

Мы оба подозревали, даже совсем недавно, что B неверно, и то, что B оказалось верным, для нас явилось сюрпризом. В самом деле, с точки зрения достаточно естественного допущения (или статистической гипотезы) B кажется довольно невероятным[198]. Мы оба сознаем, что это усиливает указанный довод в пользу A. Но один из нас говорит«лишь немного усиливает», а другой говорит «значительно усиливает», и мы сохраняем наше несогласие.

Мы оба, я полагаю, совершенно честны, и наше несогласие является не только делом темперамента. Мы не согласны[199] потому, что его фон[139] отличен от моего. Хотя у нас была приблизительно одинаковая научная подготовка, мы развивались в различных направлениях. Его работа привела его к недоверию к гипотезе A. Он, может быть, надеется, что когда-нибудь будет в состоянии опровергнуть это предположение A. Что до меня, то я не смею надеяться, что когда-нибудь докажу A. Однако я должен признаться, что хотел бы доказать A, но не хочу обманывать себя иллюзией, что когда-нибудь буду в состоянии доказать A. Такая не полностью признанная надежда может оказать влияние на мое суждение, на мою оценку веса довода. Однако я могу помимо этого иметь и другие основания: еще более неясные, едва ли сформулированные смутные основания. И мой друг может иметь какие-либо основания, в которых он еще себе не признается. Как бы то ни было, такие различия в наших фонах могут объяснить ситуацию: мы несогласны[200] в отношении силы довода, хотя мы и согласны по всем ясно осознаваемым пунктам, которые должны были бы оказывать влияние на силу указанного довода в объективном суждении в соответствии с универсально принятыми разумными стандартами[201]

Отметим: два человека, которым представлены одни и те же доводы и которые применяют одни и те же схемы правдоподобных умозаключений, могут честно быть не согласны[202].

(4) Мы пытались увидеть правдоподобные рассуждения в действии, конкретно, в поведении людей, встречающих конкретные задачи. Мы имеем теперь, я надеюсь, несколько более ясное представление о том, в каком отношении наши схемы являются «обязательными», в какой степени их можно рассматривать в качестве правил.

341

Однако имеются другие подходы к исследованию. Формальная логика и исчисление вероятностей имеют ясные строгие правила, которые представляются как-то связанными с нашими схемами. Какова природа этой связи? Вот вопрос, который мы обсудим в следующих параграфах.

2. Один аспект доказательного рассуждения. На этом этапе может быть полезным сравнение правдоподобного рассуждения с доказательным рассуждением. Однако правдоподобные рассуждения на том уровне, которого мы достигли, не могут, конечно, выдержать сравнения с чрезвычайно сложной ступенью, которой достигла теория доказательных рассуждений к настоящему времени в результате развития на протяжении более чем двух тысяч лет, из которых последние пятьдесят были особенно плодотворными. Более полезным может оказаться сравнение с более примитивным аспектом доказательного рассуждения. Поставим себя, насколько возможно, в положение современника Аристотеля.

Аристотель подметил, что рассуждения соответствуют некоторым схемам. Он наблюдал, я себе представляю, такие схемы в философских или политических или судебных или повседневных рассуждениях, узнавал эти схемы, когда они встречались, отделял от всего лишнего и формулировал их. Эти схемы — силлогизмы. Примеры, которыми Аристотель находит необходимым подкреплять свои силлогизмы, по-видимому, свидетельствуют о том, что он открыл эти силлогизмы с помощью какого-то рода индукции — а как он мог бы открыть их иначе? Как бы то ни было, идея, что силлогизмы могли быть открыты индуктивно, сближает их с нашими схемами правдоподобных рассуждений.

Вместо силлогизма «о присущем», столь дорогого Аристотелю и еще более дорогого его схоластическим последователям, рассмотрим «modus tollens» «гипотетического» силлогизма, который мы уже рассматривали в § 12.1:

Из A следует B

B ложно

A ложно

Даже с крайне примитивной точки зрения мы можем увидеть у этой схемы рассуждения различные замечательные свойства: она объективна, универсальна, самостоятельна и окончательна.

(1) Пользуясь словом объективна, мы подчеркиваем, что справедливость рассуждения не зависит от личности рассуждающего, от его настроения или вкуса или класса или убеждений или цвета кожи.

(2) Пользуясь словом универсальна, мы подчеркиваем, что рассматриваемые утверждения (обозначенные буквами A и B) не обязаны

342

принадлежать к той или иной специальной области знаний, к математике или физике, юриспруденции или логике, но могут принадлежать к любой из этих областей или вообще к какой угодно области. Они могут относиться к любому достаточно ясному объекту человеческих размышлений: силлогистическое умозаключение применяется ко всем таким объектам.

(3) Чтобы понять следующий пункт, нам следует ясно осознать, что наши знания и наши разумные представления под влиянием новой информации могут измениться. Однако в рассматриваемом силлогизме есть нечто неизменное. Раз мы приняли посылки, мы не можем получить новую информацию относительно затронутых в нашем силлогистическом рассуждении объектов. Если, однако, эта информация не меняет того факта, что мы принимаем заключение. Умозаключение демонстративного силлогизма не требует ничего постороннего; оно независимо от чего бы то ни было, не упомянутого в посылках. В этом смысле силлогизм самостоятелен: ничего кроме посылок не нужно, чтобы сделать законное заключение, и ничто не может сделать его незаконным, если посылки остаются прочными.

Эта «самостоятельность», или «автаркия» силлогизма является, возможно, его наиболее заслуживающим внимания свойством. Процитируем самого Аристотеля: «Силлогизм же есть высказывание, в котором при утверждении чего-либо из него необходимо вытекает нечто отличное от утвержденного и именно в силу того, что это есть. Под словами же „в силу того, что это есть“ я разумею, что это отличное вытекает благодаря этому, а под словами „вытекает благодаря этому“ — что оно не нуждается ни в каком постороннем термине, чтобы следовать с необходимостью»[140].

(4) Если посылки неоспоримо достоверны, то мы можем «отделить заключение от силлогизма. Иными словами, если вы достоверно знает и что «из A следует B», и что «B ложно», то вы можете забыть об этих посылках и сохранить только заключение «A ложно» в качестве вашего окончательного умственного владения.

Мы исследовали только один из нескольких видов силлогизмов, но исследованный силлогизм является типичным: и другие силлогизмы также объективны, универсальны, самостоятельны и окончательны. И эти свойства обрисовывают общий характер доказательного рассуждения.

3. Соответствующий аспект правдоподобного рассуждения. Сравним схему доказательного рассуждения («modus tollens»), рассмотренную в предыдущем параграфе, со схемой правдоподобного

343

рассуждения, введенной в § 12.1:

Из A следует B

B истинно

A более правдоподобно

Между этими двумя схемами, «доказательной» и «правдоподобной», существует некоторое внешнее сходство. (Доказательная схема традиционна, а вторая схема, конечно, была составлена по ее образцу.) Сравним, однако, их более детально.

Обе схемы имеют одну и ту же первую посылку:

Из A следует B

Вторые посылки

B ложно B истинно

в точности противоположны, но они одинаково ясны и определенны; они находятся на одном и том же логическом уровне. Однако между двумя заключениями

A ложно A более правдоподобно

имеется огромное различие. Эти заключения находятся на разных логических уровнях. Заключение доказательной схемы находится на том же уровне, что и посылки, но заключение нашей схемы правдоподобного рассуждения другой природы является менее четким, менее полно определенным.

Правдоподобное заключение можно сравнить с механической силой, имеющей направление и величину. Это заключение толкает нас в известном направлении: A становится более правдоподобным. Это заключение имеет также известную силу: A может стать намного более правдоподобным или лишь _немножко более правдоподобным. Это заключение не полностью определено и не полностью подкреплено посылками. Направление определено и следует из посылок, а сила — нет. Для любого разумного человека посылки влекут за собой, что A становится более правдоподобным (заведомо не менее правдоподобным), но мой друг и я можем быть не согласны[203], насколько более правдоподобным становится A. Направление объективно, но сила субъективна. Мой друг и я можем честно быть не согласны[204] в отношении веса заключения, так как наши темпераменты, наши фоны[205] и наши несформулированные доводы могут быть различными. Однако сила заключения существенна. Если двое присяжных различно оценивают силу заключения, то один из них может быть за оправдание, а другой — против. Если двое ученых различно оценивают силу заключения, то один из них может быть за то, чтобы предпринять известный эксперимент[206], а другой — против[207].

344

Заключение нашей схемы правдоподобного умозаключения, когда оно сравнивается с действительными представлениями и действиями разумных людей, кажется односторонним: оно определяет только одну сторону и игнорирует другие. Если мы ясно это поймем, то природа правдоподобного рассуждения может нам казаться менее озадачивающей и неуловимой. Как бы то ни было, мы теперь лучше подготовлены к тому, чтобы сравнить наши схемы, доказательную и правдоподобную, пункт за пунктом. Каждый из следующих пунктов относится к соответствующему пункту предыдущего § 2.

(1) Когда мы рассуждаем в соответствии с нашей схемой правдоподобного умозаключения, мы следуем принципу: подтверждение следствия усиливает предположение[208]. Этот принцип, по-видимому, является общепризнанным независимо от субъективных различий и своеобразных особенностей данного человека. Таким образом, наша схема кажется объективной.

Мы расплачиваемся, однако, за такую «объективность». Нашей схеме удается быть объективной потому, что она является односторонней, ограничена одной стороной правдоподобного умозаключения. Когда мы ставим вопрос: насколько усиливается предположение в результате подтверждения этого следствия?» — мы открываем дверь для субъективных различий.

(2) На большом числе примеров в предыдущих главах мы старались показать, что, имея дело с математическими предположениями, мы естественно следуем нашей схеме правдоподобного умозаключения. Лежащий в основании принцип общепризнан в естественных науках и неявно допускается в суде и в повседневной жизни. подтверждение следствия рассматривается как разумный довод в пользу предположения в любой области. Таким образом, наша схема кажется универсальной.

Мы расплачиваемся, однако, за такую «универсальность». Нашей схеме удается быть универсальной потому, что она является односторонней, ограничена одной стороной правдоподобного умозаключения. Когда мы ставим вопрос: «Каков вес такого довода?», — эта универсальность расплывается[209]. Чтобы оценить вес довода, вы должны быть знакомы с данной областью; чтобы оценить вес с уверенностью, вы должны быть специалистом в этой области[210]. Однако вы не можете быть знакомы со всеми областями и еще менее вы можете быть специалистом во всех областях. И, таким образом, каждый из нас достаточно быстро заметит, что имеются практические пределы универсальности правдоподобного умозаключения.

(3) Правдоподобное заключение, в той мере, в какой оно определено, подкрепляется посылками. На основании доводов, которые даются посылками, разумно относиться к A с большей уверенностью. Когда-нибудь позже, однако, мы можем получить новую информацию, которая, не меняя нашей уверенности в посылках, может изменить

345

наше мнение об A.: мы можем найти A менее правдоподобным или же нам, может быть, даже удастся доказать, что A ложно.

Это не является возражением против нашей схемы рассуждения: насколько сохраняют силу доводы, выраженные в посылках, заключение оправдано. Вердикт присяжных может осудить невиновного и оправдать преступника. Однако такую несправедливость вердикта можно простить: на основании имеющихся в распоряжении улик не был возможен никакой лучший вердикт[211]. Такова природа правдоподобного умозаключения, и, таким образом, наша схема правдоподобного умозаключения может быть, названа самостоятельной.

Однако этот вид самостоятельности, или «автаркии» еще не означает неизменной прочности. Сверх того, вес довода, не упоминаемый в заключении нашей (односторонней) схемы, но тем не менее важный, зависит от чего-то, не упоминаемого[212] в посылках. Сила заключения (не его направление) требует чего-то, находящегося вне посылок.

(4) Мы не можем «отделить» заключение нашей схемы правдоподобного рассуждения. Слова «A делается более правдоподобным» лишены смысла без тех посылок, которые объясняют, ввиду каких обстоятельств оно таким делается. Вместе с посылками правдоподобное заключение получает совершенно ясный смысл и является совершенно разумным, но его ценность может с течением времени уменьшиться, хотя посылки остаются в неприкосновенности. Правдоподобное заключение может быть очень ценным в момент, когда оно возникало, но увеличение знаний, вероятно, уменьшит его ценность: его значение кратковременно, преходяще, недолговечно, условно.

Короче, наша схема правдоподобного рассуждения является односторонней и оставляет достаточных простор для несогласия в отношении существенных вещей. Однако ценой такой односторонности ей удается быть объективной и универсальной, даже в известной степени самостоятельной. Все же она не может избежать того, чтобы быть только условной.

Было бы глупо жалеть, что в некоторых отношениях нашей схеме правдоподобного рассуждения недостает совершенства доказательного рассуждения. Напротив, мы должны были бы испытывать некоторое удовлетворение из-за того, что нам удалось в известной степени выяснить различие, о котором мы могли подозревать с самого начала.

С самого начала было ясно, что эти два вида рассуждений имеют разные задачи. С самого начала они казались очень различными: доказательное рассуждение казалось определенным, окончательным, «машиноподобным», а правдоподобное рассуждение — смутным, условным, специфически «человеческим». Теперь мы можем видеть различие немного отчетливее. В противоположность доказательному умозаключению, правдоподобное умозаключение оставляет неопределенным в высшей степени существенный пункт: «силу», или «вес» заключения. Этот вес может зависеть не только от выясненных

346

оснований, таких, как основания, выраженные в посылках, но и от невыясненных, невыраженных оснований где-нибудь в фоне человека, выводящего заключение. У человека есть фон, а у машины его нет. Действительно, вы можете построить машину, которая выводила бы за вас доказательные заключения, но, я думаю, вы никогда не сумеете построить машину, которая будет выводить правдоподобные заключения[213].

4. Один аспект исчисления вероятностей. Трудности. В высшей степени важным шагом в построении физической теории является ее формулировка в математических терминах. Мы подошли к тому месту нашего исследования, где нам следует предпринять такой шаг: нам следует сформулировать наши взгляды на правдоподобные рассуждения в математических терминах.

Никакая попытка сформулировать теорию правдоподобных рассуждений не может игнорировать исторический факт: исчисление вероятностей рассматривалось Лапласом и многими другими выдающимися учеными в качестве подходящего выражения плавил правдоподобных умозаключений. Имеются определенные доводы в пользу такого мнения и известные возражения против него. Мы начнем с рассмотрения некоторых трудностей.

Мы хотим воспользоваться исчислением вероятностей, чтобы сделать более точными наши взгляды на правдоподобные рассуждения. Однако мы могли бы иметь в этом отношении кое-какие опасения, потому что в предыдущей главе мы видели, что исчисление вероятностей является (вполне приемлемой) теорией случайных массовых явлений. Как могло бы исчисление вероятностей быть и теорией массовых явлений, и логикой правдоподобных умозаключений?

Это несерьезное[214] возражение: здесь нет реальной трудности. Исчисление вероятностей могло бы быть и тем, и другим, могло бы иметь две интерпретации. Действительно, математическая теория может иметь несколько различных интерпретаций. Одно и то же дифференциальное уравнение (уравнение Лапласа) описывает установившееся безвихревое течение несжимаемой идеальной жидкости и распределение сил в электростатическом поле. то же самое уравнение описывает также остановившееся течение тепла, установившееся течение электричества, диффузию соли, растворенной в воде при подходящих условиях, и другие явления. И, таким образом, a priori не исключено, что одна и та же математическая теория может служить двум целям. Возможно, мы можем пользоваться исчислением вероятностей и при описании случайных массовых явлений и при систематизации наших правил правдоподобных умозаключений.

Важно, однако, ясно различать эти две интерпретации. Таким образом, мы можем пользоваться символом P{A} (см. пример 14.26) в обеих интерпретациях, но только с некоторыми предосторож-

347

ностями, и мы должны с полной ясностью понимать оба значения этого символа и видеть различие между этими двумя значениями.

В предыдущей главе о случайных массовых явлениях мы рассматривали некоторого рода событие A, как, например, рождение мальчика или падение дождевой капли в указанном месте или выпадение указанного числа очков на игральной кости и т. д. Мы пользовались символом P{A} для обозначения вероятности события A, т. е. теоретического значения относительной частоты дальнего действия события A.

В настоящей главе, однако, мы должны иметь дело с правдоподобными рассуждениями. Мы рассматриваем некоторое предположение A и интересуемся надежностью[215] этого предположения A, силой доводов в пользу A нашей уверенностью в A, степенью доверия, которое нам следовало бы иметь к A, короче, правдоподобностью[141][216] предположения A. Мы воспользуемся символом P{A} для обозначения правдоподобности A.

Итак, в настоящей главе, если ясно не высказано противное, мы будем пользоваться символом P{A} в его втором значении в качестве «правдоподобности». Такое употребление этого символа не является предосудительным, но мы должны тщательно обсудить понятие правдоподобности, если не желаем услышать серьезных возражений.

Прежде всего нужно избежать двусмысленности. Символ P{A} должен представлять правдоподобность A, или силу доводов в пользу предположения A[217]. Такие доводы являются сильными, если они убедительны. Они убедительны, если кого-либо убеждают. Однако мы не сказали, кого они должны были бы убеждать: вас или меня или м-ра Смита или м-с Джонс или кого-нибудь еще? Силу этих доводов можно было бы также понимать объективно. Если мы так ее и понимаем, то степень веры в рассматриваемое предположение, которую можете случайно иметь вы или я или любой человек, несущественна, но что существенно — это степень разумной веры, которую любой из нас должен иметь. Мы не сказали, однако, и должны еще решить, в каком точном смысле нам следует пользоваться термином «правдоподобность A» и соответствующим символом P{A}.

Имеется другая трудность. Величины, рассматриваемые физиками, например, «масса, «Электрический заряд или «скорость реакции», имеют операционное определение; физик точно знает, какие операции он должен произвести, если желает, например, установить величину электрического заряда. Определение «относительной частоты дальнего действия», хотя в каком-то отношении и менее четко, чем определение электрического заряда, все же является операционным; оно подсказывает определенные операции, которые мы должны

348

выполнить, чтобы получить приближенное числовое значение такой частоты. Затруднение с понятием «правдоподобности предположения» состоит в том, что мы не знаем для нее[218] никакого операционного определения. Какова правдоподобность предположения, что м-р Джонс неверен своей жене? Эта правдоподобность может в данный момент в уме м-с Джонс иметь определенное значение (мы надеемся, ничтожно малое значение), но мы не знаем, как это значение определить численно. Какова правдоподобность закона всемирного тяготения, оцениваемая на основании наблюдений, изложенных в первом издании Начал Ньютона? Этот вопрос для некоторых из нас (возможно, не для м-с Джонс, но для Лапласа или Кейнса, если бы они еще были живы, — см. эпиграфы, предпосланные этой главе) мог бы представлять большой интерес. Но никто не отважился предложить для такой правдоподобности определенное числовое значение[219].

Мы должны еще дать подходящую интерпретацию термина«правдоподобность предположения A» и соответствующего символа P{A}. Эта интерпретация должна быть такой, чтобы трудность операционного определения не служила для нее препятствием. Кроме того, и это главное, эта интерпретация должна дать нам возможность рассматривать правила правдоподобных рассуждений систематически и реалистично.

5. Один аспект исчисления вероятностей. Попытка. Вы только что были представлены м-ру Кто-нибудь и должны сказать ему несколько слов. Вы оба совершенно незнакомы друг с другом. И поэтому ваш разговор, вероятно, будет осторожным. Тем не менее вы не можете не затронуть различных утверждений вроде «Завтра будет дождь». «Следующую Большую Игру выиграют Синие», Корпорация Такая-то выплатит в будущем году более высокие дивиденды», «М-с Некто, о разводе которой говорят в городе, изменяла своему мужу», «Полиомиелит вызывается вирусом» или каких-нибудь других утверждений A, B, C, D, E, … М-р Кто-нибудь приписывает утверждению A определенную степень веры P{A}. Если вы очень умны, то после некоторого времени, проведенного с м-ром Кто-нибудь, вы можете почувствовать высока ли P{A} или низка. Каким бы, однако, вы ни были умным, я не могу поверить, что вы в состоянии приписать P{A}, правдоподобности утверждения A в глазах м-ра Кто-нибудь, определенное числовое значение. (Хотя это было бы интересно; значения P{A}, P{B}, P{C}, … могли бы метко охарактеризовать личность м-ра Кто-нибудь.)

Будем реалистичны и признаем невозможность задачи, которая, очевидно, находится за пределами наших средств: рассмотрим P{A}, правдоподобность предположения A в глазах м-ра Кто-нибудь как определенную положительную дробь:

0 < P{A} < 1,

349

числового значения которой, однако, мы не знаем. И подобным же образом будем интерпретировать P{B}, P{C}, …, если B, C, … — предположения, т. е. ясно сформулированные (возможно, математические) утверждения, относительно которых, однако, м-р Кто-нибудь к настоящему времени не знает, истинных они или ложны. Если, однако, A истинно и м-р Кто-нибудь это знает, то положим P{A} = 1. Если же A, однако, ложно и м-р Кто-нибудь это знает, то положим P{A} = 0.

Мне кажется, что наше незнание числовых значений P{A}, P{B}, … не может нам реально повредить. Фактически, мы не интересуемся здесь личными мнениями м-ра Кто-нибудь. Мы интересуемся объективными и универсальными правилами правдоподобных умозаключений. Мы хотим прежде всего знать, существуют ли такие правила вообще, а затем мы хотим знать, раскрывают ли такие правила исчисление вероятностей (что отстаивал Лаплас и другие). В настоящий момент мы скорее надеемся, что такие правила имеются и что м-р Кто-нибудь как разумный человек в соответствии с такими правилами заключает, какие степени веры P{A}, P{B}, P{C}, … он в данным момент приписать рассматриваемым утверждениям A, B, C, … И, таким образом, я не могу понять, почему бы наше незнание числовых значений P{A}, P{B}, P{C}, … должно было нам повредить.

Попытаемся же применить в соответствии с этой интерпретацией правила исчисления вероятностей к правдоподобностям P{A}, P{B}, P{C}, … — положительным дробям, измеряющим степени уверенности этого мифического или идеализированного человека, м-ра Кто-нибудь. Мы хотим понять, можем ли бы, так поступая, извлечь что-либо, что мы могли бы разумно истолковать как объективное и универсальное правило правдоподобных рассуждений. Наша попытка может, конечно, не удаться, но я не могу в этот момент понять, почему бы она должна была не удаться, и, таким образом, я осторожно надеюсь[142].

6 Исследование следствия. М-р Кто-нибудь исследует некоторое предположение A. Это предположение A ясно сформулировано, но м-р Кто-нибудь не знает, истинно ли A или нет, и очень хочет узнать,

350

как обстоит дело: истинно A или ложно? Он подмечает некоторое следствие B предположения A. Он убеждается, что

Из A следует B

Однако он не знает, истинно B или ложно, и иногда, когда он устает исследовать A, он думает переключиться на исследование B.

Эту ситуацию мы рассматривали много раз, и теперь мы хотим рассмотреть ее в свете исчисления вероятностей. Мы хотим обратить должное внимание на три правдоподобности: P{A}, P{B} и P{A/B}. М-р Кто-нибудь очень хорошо знает, что A и B не доказаны и не опровергнуты, но он до некоторой степени в них верит, и степень его веры выражается соответственно правдоподобностями P{A} и P{B}. В его размышлениях играет важную роль и P{A/B}, степень веры, которую он мог бы приписать A, если бы знал, что B истинно.

У нас нет никаких средств приписать любой из этих правдоподобностей числовое значение, хотя мы иногда можем себе представить, в каком направлении изменение в состоянии знаний м-ра Кто-нибудь изменило бы значение той или иной правдоподобности. Как бы то ни было, исчисление вероятностей дает связь между ними.

В самом деле, по одной из фундаментальных теорем о вероятностях [см. пример 14.26 (2)],

P{A}P{B/A} = P{B}P{A/B}.

Но теперь, так как из A следует B, то если A истинно, должно быть истинным и B и, таким образом,

P{B/A} = 1.

Отсюда мы получаем

P{A} = P{B}P{A/B}. (I)

Представим себе отчетливо, что это равенство означает.

(1) М-р Кто-нибудь решил исследовать следствие B своего предположения A. Ему все же не удалось довести это исследование до заключения. Однако иногда он видел указания, что B может быть истинно, а иногда — указания на обратное. Его уверенность в B, которую мы обозначаем символом P{B}, соответственно, возрастала и падала. Однако он не заметил ничего, что изменило бы его мнение о соотношении между A и B, или о P{A/B}. Какое влияние все это оказывает на P{A}, его уверенность в A?

Равенство (I) показывает, что если P{A/B} остается неизменной, то P{A} изменяется в том же направлении, что и P{B}. Это согласуется с нашими прежними замечаниями, в частности, с замечаниями в § 13.6. (Заметьте, что мы рассматриваем только направление изменения, которое иногда мы можем установить, а не величину, которую мы никогда не можем знать точно.)

351

(2) М-ру Кто-нибудь удалось доказать B, являющуюся следствием предположения A, которое мы первоначально исследовали. Перед тем как доказать B, он имел некоторую уверенность в B, степень которой мы обозначим символом P{B}; он имел также некоторую уверенность в A, степень которой есть P{A}. Иногда он рассматривал P{A/B}, уверенность в A, которую он имел бы после доказательства B. После доказательства B его уверенность в B достигает максимального значения 1 и его уверенность в A становится равной P{A/B}. (Подставляя 1 вместо P{B} в равенство (I), мы формально приходим к новому значению правдоподобности A.) Мы допускаем здесь, что его мнение о соотношении между A и B остаются неизменными.

Замечая, что если B не доказано и не опровергнуто, то 0 < P{B} < 1, из равенства (I) выводим неравенство

P{A} < P{A/B}. (II)

Здесь P{A} и P{A/B} представляют, соответственно, правдоподобность A до и после доказательства B. Поэтому неравенство (II) является формальным выражением принципа, с которым мы так часто встречались: подтверждение следствия делает предположение более правдоподобным; ср., например, § 12.1.

(3) Но мы можем на равенстве (I), которое мы запишем в виде

научиться большему. Левая часть, правдоподобность A после подтверждения B, выражается через уверенности, соответственно, в A и в B, которые исследователь имеет до такого подтверждения. Сравним различные случаи успешного подтверждения следствия[220]. Во всех этих случаях имеет место одно общее обстоятельство: до подтверждения следствия B предположения A (которому посвящено исследование) мы относились к предположению A с одной и той же уверенностью P{A}. Однако эти случаи отличаются в другом отношении: следствие B (которое было в конечном счете подтверждено) в одних случаях ожидалось с большей уверенностью, а в других с меньшей[221]. Иначе говоря, мы рассматриваем P{A} как постоянную, а P{B} — как переменную. Какое влияние оказывает изменение P{B} на вес доводов, получающихся в результате подтверждения следствия B?

Обратим должное внимание на крайние случаи. Так как B является следствием A, то B, несомненно, истинно, когда A истинно и, таким образом, P{B}, правдоподобность B, не может быть меньше, чем P{A} правдоподобность A. С другой стороны, никакая правдоподобность не может превышать достоверности[222]: P{B} не может быть больше, чем 1. Мы определили границы, между которыми

352

содержится P{B}:

P{A} ≤ P{B} < 1.

Нижняя граница достигается, когда не только A следует из B, но и из B следует A, т. е. когда оба утверждения: A и B — равнозначны, стоят и рушатся вместе; в этом случае, конечно, они одинаково правдоподобны[223]. Верхняя граница, 1, не может в действительности достигаться: если бы она достигалась, B было бы до исследования достоверным и мы не включили бы этот случай в наше рассмотрение. Однако верхняя граница может быть приближена: B до исследования может быть почти достоверным. Как изменяются доводы, получающиеся в результате подтверждения B, когда P{B} меняется между своими крайними границами?

Эти доводы сильнее, когда P{A/B}, новая уверенность в A, получающаяся в результате подтверждения следствия B, больше.

Из соотношения (III) имеем

Когда P{B} убывает он 1 до P{A}, P{A/B} возрастает от P{A} до 1.

Это утверждение выражает на новом языке принцип, который мы признали ранее (12.3): прирост нашей уверенности в предположении, вызываемый подтверждением одного из его следствий, изменяется обратно правдоподобности следствия до такого подтверждения. Чем более неожиданно следствие, тем более весомо его подтверждение[224]. Подтверждение наиболее неожиданного следствия наиболее убедительно, тогда как подтверждение следствия, в котором мы почти при любых обстоятельствах не сомневались (P{B} почти 1), имеет в качестве довода небольшую ценность.

(4) Только что разобранную ситуацию можно рассмотреть и с другой точки зрения. Пользуясь некоторыми простыми правилами исчисления вероятностей [ср. пример 14.26, формулы (4), (2), (3) в этом порядке], получаем

P{B} = P{AB} + [P{ĀB} = P{A}P{B/A} + P{Ā}P{B/Ā} = P{A} + [1 — P{A}]P{B/Ā}.

При переходе к последней строке[225] мы пользовались тем, что P{B/Ā} = 1; это выражает тот факт, что B есть следствие A. Подставляя вместо P{B} только что выведенное значение из (III), получаем

(IV)

Допустим, как прежде, что P{A} постоянно, т. е. рассмотрим различные случаи, в которых уверенность в A, исследуемом предпо-

353

ложении, до испытания следствия B из предположения A была одной и той же. однако P{A/B}, правдоподобность A после подтверждения B, все еще зависит от P{B/Ā}, правдоподобности B (конечно, до подтверждения), рассматриваемой при допущении, что A не истинно. И P{B/Ā} может меняться; в действительности она может принимать любые значения между 0 и 1. Теперь, по нашей формуле (IV):

Когда P{B/Ā} убывает от 1 до 0, P{A/B} возрастает от P{A} до 1.

Это утверждение на новом языке выражает принцип, который мы обсуждали ранее (§ 13.10). посмотрим на крайние случаи. Если B без A едва ли правдоподобно (P{B/Ā} почти 0), то подтверждение следствия B подводит предположение A близко к достоверности[226]. С другой стороны, подтверждение следствия B, в котором мы вряд ли сомневались бы, даже если бы A было ложно (P{B/Ā} почти 1), мало прибавляет к нашей уверенности в A.

7. Исследование возможного основания. После широкого и осмотрительного обсуждения в предыдущем параграфе мы можем немного тверже перейти к обзору сходных ситуаций.

Вот ситуация такого рода: цель нашего исследования — некоторое предположение A. Мы подмечаем возможное основание для A, т. е. предположение B, из которого вытекало бы A:

A следует из B.

Начинаем исследовать B. Если бы нам удалось доказать B, то A тоже было бы доказано. Однако B оказалось ложным. Как повлияет опровержение B на нашу уверенность в A?

Пусть на этот вопрос ответит исчисление вероятностей. Так как A следует из B, то

P{A/B} = 1.

Скомбинируем это с некоторыми основными формулами [см. пример 14.26 (4), (2), (3)]:

P{A} = P{AB} + P{A^͞B} = P{B}P{A/B} + P{^͞B}P{A/^͞B} = P{B} + [1 — P{B}]P{A/^͞B}.

Отсюда получаем, что

(I)

Левая часть представляет правдоподобность A после того, как B (являющееся возможным основанием для A) было опровергнуто.

354

Правая часть относится к ситуации, имевшей место до того как B было опровергнуто. Между прочим, эта правая часть может быть преобразована так, чтобы равенство (I) приняло вид

отсюда мы видим, что

P{A^͞B} < P{A}. (II)

Обе части этого неравенства представляют правдоподобность предположения A, левая часть — после опровержения B, правая часть — до этого опровержения. Следовательно, неравенство (II) выражает правило: когда возможное основание для предположения рушится, наша уверенность в предположении может только уменьшиться (ср. § 13.2).

Однако мы можем на равенстве (I) научиться большему. Рассмотрим P{A} как постоянную, а P{B} — как переменную[227]. Иначе говоря, попытаемся обозреть различные случаи, которые отличаются друг от друга в одном важном отношении: в нашей уверенности в B[228]. Наша уверенность в B может быть очень мала, но она не может быть произвольно велика: она никогда не может превзойти нашей уверенности в A, так как если B истинно, то и A тоже истинно. (Однако A может еще быть истинным, даже если B ложно.) Итак, мы определили крайние значения, между которыми может изменяться P{B}:

0 < P{B} ≤ P{A}.

Из равенства (I) имеем:

Когда P{B} возрастает от 0 до P{A}, P{A^͞B} убывает от P{A} до 0.

Иными словами, чем с большей уверенностью мы относимся к возможному основанию нашего предположения, тем больше будет потеря веры в наше предположение, когда возможное основание будет опровергнуто.

8. Исследование противоречащего предположения. Рассмотрим теперь другую ситуацию: мы исследуем два противоречащих предположения, A и B. Когда мы говорим, что A противоречит B, или

A несовместимо с B,

Мы подразумеваем, что из истинности одного из них следует ложность другого. На самом деле в первую очередь мы интересуемся A и начали исследовать B, потому что думали, что исследование B могло бы пролить на A некоторый свет. Действительно, доказательство B опровергло бы A. Однако нам удалось опровергнуть B. Как повлияет этот результат на нашу уверенность в A?

355

Пусть даст ответ исчисление вероятностей. Начнем с выражения на языке этого исчисления того, что A и B несовместны[229]. Это, иначе говоря, означает, что A и B оба не могут быть истинны и, таким образом,

P{AB} = 0.

Теперь на основе наших формул [ср. пример 14.26 (4), (2), (3)] заключаем:

P{A} = P{AB} + P{A^͞B} = P{A^͞B} = P{^͞B}P{A^͞B}= (1— P{B}P{A/B},

что в конечном счете дает

Из равенства (I), очевидно, вытекает неравенство:

P{A^͞B} < P{A}. (II)

Левая его часть относится к ситуации после опровержения B, правая часть — к ситуации до этого опровержения. Следовательно, мы можем прочитать (II) следующим образом: когда рушится несовместное соперничающее предположение, наша уверенность в данном предположении может только возрасти (ср. § 13.3).

Однако мы можем на равенстве (I) научиться большему[230]. Рассмотрим P{A} как постоянную, а P{B} — как переменную. Определим границы, между которыми может изменяться P{B}. Конечно, P{B} может быть произвольно мала. Однако P{B} не может быть сколь угодно велика; действительно, она никогда не может превзойти P{Ā}. Если B истинно, то Ā и подавно истинно. Так как P{Ā} равна 1 — P{A}, то

0 < P{B} ≤ 1 — P{A}.

Из равенства (I) мы имеем:

Когда P{B} возрастает от 0 до 1 — P{A}, P{A/B} возрастает от P{A} до 1.

Иными словами, чем больше доверие, с которым мы относимся к несовместному сопернику нашего предположения, тем больше будет прирост веры в наше предположение, когда этот соперник будет опровергнут.

9. Исследование одного за другим нескольких следствий. Рассмотрим теперь следующую важную ситуацию: целью нашего исследования является некоторое предположение A. К данному моменту мы не видим, как мы могли бы решить, истинно A или нет. Однако

356

мы видим несколько следствий B₁, B₂, B₃, … предположения A: из A следует B₁, из A следует B₂, из A следует B₃, …. Следствия B₁, B₂, B₃, … более доступны, чем само A[231], и мы принимаемся их исследовать одно за другим. (Это типичный прием естествознания: мы не имеем никаких средств для исследования общего закона A самого по себе, и поэтому мы исследуем его посредством испытания нескольких следствий.) Мы уже исследовали следствия B₁, B₂, …, B_n, и нам удалось их все подтвердить: B₁, B₂, …, B_n оказались истинными. Теперь мы испытываем еще одно следствие B_{n + 1}. Какое влияние исход испытания окажет на нашу уверенность в A?

Чтобы найти ответ в свете исчисления вероятностей, начнем с одного общего правила этого исчисления [см. пример 14.26 (5)]:

P{A/H}P{B/HA} = P{B/H}P{A/HB}.

Положим B = B_{n + 1}. Теперь, так как B_{n + 1} является следствием A,

P{B/HA} = P{B_{n + 1}/HA} = 1,

и, таким образом, мы находим, что

P{A/H} = P{B_{n + 1}/H}P{A/HB_{n + 1}}.

Положив H = B₁, B₂, …, B_n, получим решающую формулу:

P{A/B₁ … B_n} = P{B_{n + 1}/B₁ … B_n}P{A/B₁ … B_nB_{n + 1}} (I)

Чтобы правильно понять (I), мы должны ясно себе представлять, что

P{A/B₁ … B_n} и P{B_{n + 1}/B₁ … B_n},

Соответственно, обозначают правдоподобности

A и B_{n + 1} после того, как были подтверждены B₁, B₂, …, B_n, но, конечно, до того, как было подтверждено B_{n + 1}; P{A/B₁ … B_nB_{n + 1}} обозначает правдоподобность A после подтверждения его n + 1 следствия B₁, B₂, …, B_n и B_{n + 1};

Мы должны помнить значение этих символов[232], и тогда мы можем читать (I) как точное и содержательное предложение об индуктивных рассуждениях.

Сосредоточим свое внимание прежде всего на P{B_{n + 1}/B₁ … B_n}; значение этой правдоподобности в большинстве случаев будет меньше 1, и оно будет равно 1 только в том случае, если правильность B₁, B₂, …, B_n делает достоверной правильность B_{n + 1}, т. е. если из B₁, B₂, …, B_n вместе взятых следует B_{n + 1}. Если это не так, то из (I) мы можем вывести неравенство

P{A/B₁ … B_n} < P{A/B₁ … B_nB_{n + 1}}.

Иными словами, если новое следствие не вытекает из ранее подтвержденных следствий, то подтверждение нового следствия увеличивает нашу уверенность в предположении.

357

Напишем равенство (I) в форме:

Левая часть относится к ситуации подтверждения B_{n + 1}; правая часть относится к ситуации до этого подтверждения. Рассмотрим связь A с B₁, B₂, …, B_n как фиксированную, а связь B_{n + 1} с B₁, B₂, …, B_n — как переменную. Тогда мы можем прочитать (III) следующим образом: увеличение нашей уверенности, вызываемое подтверждением нового следствия (или вес[233] доводов, даваемых этим подтверждением), изменяется обратно правдоподобности нового следствия, оцениваемой (конечно, до его подтверждения) в свете ранее подтвержденных следствий.

Мы можем выразить то же правило другими словами. Когда мы начинаем испытывать следствие B_{n + 1} нашего предположения A, мы сталкиваемся с возможностью того, что B_{n + 1} окажется ложным и в этом случае A будет опровергнуто. Принимая во внимание ранее подтвержденные следствия B₁, B₂, …, B_n, шансы подорвать A, доказав, что B_{n + 1} ложно, кажутся сильными, когда P{B_{n + 1}/B₁ … B_n} мала. Поэтому мы можем прочитать (III) следующим образом: чем больше шансов опровергнуть рассматриваемое предположение имеет следствие, если судить по предыдущим подтверждениям, тем более сильные индуктивные доводы оно дает, если подтверждается несмотря на предчувствия. Еще короче: «чем больше опасность, тем больше чести». Если предположение избежит опасности быть опровергнутым, то его должны ценить пропорционально имевшемуся риску[234].

С самого начала нашего обсуждения мы рассматривали индуктивные доводы, даваемые последовательными подтверждениями нескольких следствий данного предположения. Крайние случаи были наиболее бросающимися в глаза. Просмотрим их еще раз (добавляя лишь немножко красок) и сосредоточим свое внимание на моменте, когда, подтвердив следствия B₁, B₂, …, B_n предположения A, мы начинаем внимательно рассматривать новое следствие B_{n + 1}.

Новое следствие B_{n + 1}, которое мы рассматриваем, может казаться «мало отличающимся» от ранее подтвержденных следствий B₁, B₂, …, B_n. Такой случай не слишком интересен. Мы с уверенностью ожидаем (по аналогии, предположительно), что B_{n + 1}, подобно другим следствиям, подтвердится (т. е. P{B_{n + 1}/B₁ … B_n} близка к 1, своему максимуму). Мы едва ли ожидаем, что исследование B_{n + 1}, обнаружит какую-нибудь совсем новую сторону или что оно опрокинет предположение A, но зато, когда B_{n + 1} в конце концов подтверждается, доводы в пользу A не очень усиливаются.

С другой стороны, новое следствие B_{n + 1}, которое мы рассматриваем, может казаться «очень отличающимся» от ранее подтвержденных следствий B₁, B₂, …, B_n. Такой случай может быть интересным. Аналогия с B₁, B₂, …, B_n дает нам мало оснований ожидать, что

358

B_{n + 1} подтвердится (P{B_{n + 1}/B₁ … B_n} близка к своему минимуму). Мы ясно понимаем, что исследование B_{n + 1} рискует опрокинуть предположение A, но оно имеет также шансы обнаружить какую-нибудь новую сторону и когда в конечном счете B_{n + 1} подтверждается, доводы в пользу A могут значительно усилиться.

Читателю следует просмотреть некоторые из наших прежних примеров и рассуждений (ср. §§ 3.1—3.7, гл VI, § 12.2, § 13.11 и несколько других мест). После должного сравнения равенство (III) настоящего параграфа, возможно, покажется ему наиболее сжатым и точным выражением принципа, о котором идет речь. Как бы то ни было, если он сможет понять значение равенства (III) на некоторых из наших примеров, то он сделал хороший шаг в направлении выяснения своих представлений о важном вопросе.

10. О косвенных уликах[235]. Рассмотрим теперь ситуацию, с которой мы встречались, когда занимались рассуждениями на юридические темы: исследуем предположение A. (Это предположение A может быть обвинением, выдвинутым обвинителем.) Мы (присяжные) должны выяснить, верно A или нет. Представлено (обвинителем) на рассмотрение обстоятельство B, так связанное с предположением A, что

B вместе с A более правдоподобно, чем без A.

На протяжении процесса это обстоятельство B так сильно подтвердилось, что мы можем его рассматривать как доказанный факт. (Возможно, что B даже не оспаривалось защитой.) Какое влияние все это окажет на нашу веру в A?

Пусть ответ на этот вопрос ответит исчисление вероятностей. Существенное допущение о связи между A и B выражается неравенством

P{B/A} > P{B/Ā}. (I)

По основным формулам теории вероятностей (ср. пример 14.26)

P{A}P{B/A} = P{B}P{A/B}, P{B} = P{A}P{B/A} + (1 — P{A})P{B/Ā}.

Из этих двух равенств получаем

Пользуясь (I), из (II) заключаем, что

P{A} < P{A/B}. (III)

Обе части этого неравенства представляют правдоподобности предположения A, левая часть — до подтверждения обстоятельства B, правая часть — после подтверждения B. Следовательно, неравенство (III) выражает правило: если какое-либо обстоятельство более правдоподобно вместе с некоторым предположением, чем без него,

359

то подтверждение этого обстоятельства может только увеличить правдоподобность этого предположения. (Ср. § 13.13.)

Мы можем на равенстве (II) научиться большему. Будем рассматривать P{A} и P{B/A} как постоянные, а P{B/Ā} как переменную. Тогда P{A/B} зависит от P{B/Ā}:

Когда P{B/Ā} убывает от P{B/A} до 0, P{A/B} возрастает от P{A} до 1.

Иными словами, чем менее правдоподобным кажется обстоятельство без некоторого предположения, тем более подтверждение этого обстоятельства увеличит правдоподобность этого предположения. Рассмотрение примеров в § 13.13 очень близко подвело нас к этому правилу.

Результатом нескольких доказанных совпадений, если все эти совпадения указывают на одно и то же заключение, являются сильные судебные улики; см. § 13.13 (4). Если имеется несколько обстоятельств B₁, B₂, B₃, …, каждое из которых более правдоподобно вместе с A, чем без A, и если они одно за другим подтверждаются, то улики в пользу A с каждым шагом возрастают. Вес добавочных улик, возникающих в результате доказательства, зависит от различных условий. Особый вес имеет новое обстоятельство, которое очень отличается от ранее исследованных обстоятельств (новый свидетель, явно независимый от ранее допрошенных свидетелей). Мы могли бы выразить эти условия, введя в рассмотрение формулы, так же не связанные формулами, введенными в настоящем параграфе, как формулы, полученные в § 9, связаны с формулами, введенными в § 6.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ XV

1. Исследуйте ситуацию, обсуждавшуюся в § 13.8, с помощью исчисления вероятностей.

2. Исследуйте схему, встретившуюся в решении примера 13.8, с помощью исчисления вероятностей.

3. Вновь исследуйте примера 13.10 с помощью исчисления вероятностей.

4. Вероятность и правдоподобность[236]. Своеобразное «неколичественное» применение исчисления вероятностей, изложенное в §§ 5—10, было задумано, чтобы объяснить некоторые схемы правдоподобных рассуждений. Эти схемы были подсказаны, главным образом, эвристическими рассуждениями по поводу математических предположений. Можем ли мы таким образом применить исчисление вероятностей к примерам другого типа?

(1) Пусть A_n обозначает предположение, состоящее в том, что на честной игральной кости, которую я собираюсь бросать, выпадет n очков (n = 1, 2, …, 6)[237]. Предположения A₁, A₂, … A₆ принадлежат к такому типу, который мы не хотели специально исследовать в §§ 5—10. однако попытаемся рассмотреть их тем же способом: рассмотрим их правдоподобности P{A₁}, P{A₂}, …, P{A₆} и применим к ним исчисление вероятностей. Поскольку A₁, A₂, … A₆ взаимно исключают одно другое и исчерпывают все возможности[238],

P{A₁} + P{A₂} + … + P{A₆} = 1.

360

Так как кость, о которой идет речь, честная[239], то ее грани взаимозаменяемы, никакая из этих шести граней не имеет преимуществ по сравнению с любой другой гранью, и, таким образом, мы вынуждены допустить, что

P{A₁} = P{A₂} = … = P{A₆} = 1/6,

и, таким образом, мы приписали рассматриваемым правдоподобностям определенные числовые значения. М-р Кто-нибудь[240] (наш друг из § 5), я думаю, пришел бы к тому же самому заключению.

Оказывается правдоподобность предположения A₁ имеет такое же числовое событие, как и вероятность события, как и вероятность события, состоящего в том, что на честной кости выпадет одно очко. Но это совсем не удивительно: мы приняли те же правила и допустили ту же взаимозаменяемость (или симметрию) при вычислении правдоподобностей, что и для вероятностей. (Читатель не должен, конечно, забывать, что правдоподобность и вероятность определяются совершенно по-разному[241].)

(2) Предыдущие соображения относятся и ко многим другим случаям.

Тремя прямыми, проходящими через центр круга, круг делится на шесть равных секторов. Дождевая капля должна упасть на поверхность этого круга. Пусть A₁ — утверждение, состоящее в том, что капля упадет на первый сектор, A₂ — что она упадет на второй сектор и т. д. Здесь ситуация, по существу, та же, что и ситуация, рассмотренная в (1), и результат, конечно, тоже одинаков: каждое из шести утверждений A₁, A₂, … A₆ имеют одну и ту же правдоподобность 1/6. Обобщение очевидно: нам не нужно придерживаться числа 6 и дождевых капель. Мы можем разделить круг на n секторов и рассмотреть случайное событие какого-нибудь другого типа. Мы можем также перейти от круга к окружности, и, таким образом, мы приходим к следующей ситуации: точка будет случайно выбираться на окружности, причем никакая конкретная точка этой окружности не имеет никакого преимущества по сравнению с другими точками. Некто предполагает, что эта точка будет лежать на определенной дуге. Правдоподобность этого предположения равна отношению длины взятой дуги к длине всей окружности[242].

От окружности мы можем перейти к сфере. Допустим для простоты, что поверхность Земли есть настоящая сфера и что метеориты, падающие на Землю, не оказывают предпочтения никакому конкретному направлению. Некто предполагает, что следующий метеорит, падающий на Землю, попадет в определенную область. Какова правдоподобность этого предположения?[243] Математическое рассмотрение может быть более сложным, если мы проведем его в мельчайших подробностях, но результат так же интуитивно понятен, как и для окружности, искомая правдоподобность равна отношению площади этой области к площади всей поверхности сферы.

Нам нет необходимости переходить к дальнейшим аналогичным или более общим ситуациям. Рассмотрим, однако, два частных случая.

Правдоподобность предположения, что точка, выбранная наугад на окружности, будет лежать на расстоянии одного градуса от данной точки окружности, равна 1/180.

Правдоподобность предположения, что следующий метеорит, падающий на землю, упадет на расстоянии одного градуса от центра Нью-Йорка, равна 0, 00007615. (Это — отношение площади малой сферической площадки к площади всей поверхности сферы.)

Окружность и сфера обладают высокой степенью симметрии: подходящим вращением, не изменяющим положения фигуры как целого, точку этой фигуры можно перевести из любого данного положения на фигуре в любое другое данное положение. Этой симметрии самой по себе не достаточно[244], чтобы оправдать предыдущие результаты. При их выводе мы должны допустить «физическую» симмет-

361

рию, взаимозаменяемость любых двух точек геометрической фигуры по отношению к рассматриваемому физическому действию[245].

Вычисленные правдоподобности не могут претендовать на значительную новизну: они совпадают с соответствующими вероятностями, давно известными и успешно применявшимися к различным массовым явлениям.

Может показаться, что вычисленные правдоподобности не способны вступить в противоречие с теми правдоподобностями, которыми мы в первую очередь интересуемся. В этом, однако, не следует чувствовать себя слишком уверенным.

(3) Кеплер[246] знал только шесть планет, обращающихся вокруг Солнца, и даже придумал геометрическую аргументацию, почему должно быть в точности шесть планет; см § 11.5. Однако телескопы не послушались его аргументации. В 1781 году, приблизительно через 150 лет после смерти Кеплера, астроном Гершель заметил медленно движущуюся звезду и предположил, что это комета; но она оказалась седьмой планетой (Ураном), обращающейся за орбитой Сатурна. В 1801—1806 годах подобным же образом были открыты четыре малые планеты (Церера, Паллада, Юнона и Веста) между орбитами Марса и Юпитера. (Сотни таких малых планет были открыты позднее.)

На основании теории Ньютона[247] астрономы пытались вычислить движение этих планет. Им это не особенно удавалось с планетой Уран; различия между теорией и наблюдениями казались превосходящими допустимые пределы ошибки. Некоторые астрономы подозревали, что эти отклонения могут быть вызваны притяжением планеты, обращающейся за орбитой Урана, и французский астроном Леверье[248] исследовал это предположение тщательнее, чем его коллеги. Исследуя различные предложенные объяснения, он нашел, что имеется только одно, которое могло бы объяснить наблюдаемые неправильности в движении Урана: существование за-урановой планеты. Он попутался вычислить орбиту такой гипотетической планеты, исходя из неправильностей урана. В конце концов Леверье удалось указать гипотетической планете определенное положение на небе. Он написал об этом другому астроному, обсерватория которого была наилучшим образом оборудована для исследования этой части неба. Письмо пришло 23 сентября 1846 года, а вечером того же дня новая планета была найдена в пределах одного градуса от места, указанного Леверье. Это была большая за-урановая планета, которая имела приблизительно массу и орбиту, предсказанные Леверье.

(4) Теория, делающая возможным такое необычайное предсказание, должна быть замечательной теорией. Это может быть нашим первым впечатлением. Попытаемся сделать это впечатление более ясным с помощью исчисления вероятностей.

Пусть T обозначает теорию, лежащую в основании астрономических вычислений: это — теория Ньютона, состоящая из его законов механики и его закона всемирного тяготения[249].

Пусть N обозначает утверждение Леверье: в данный день в окрестности такой-то точки неба должна находиться новая планета, имеющая (приблизительно) такую-то массу и такую-то орбиту. Точнее, пусть N обозначает ту часть утверждения Леверье, которая была подтверждена последующими наблюдениями.

Пусть P{T} обозначает степень уверенности в теории T, основанную на всех фактах, известных астрономам до открытия новой планеты.

Пусть P{T/N} обозначает степень уверенности, вызываемую той же теорией T, когда к фактам, известным ранее прибавилось подтверждение предсказания Леверье N.

Мы думаем, что подтверждение предсказания Леверье увеличивает доверие к теории T, и, таким образом, мы подозреваем, что P{T/N} больше, чем P{T}. Действительно, мы находим [ в силу примера 14.26 (2)], что

Здесь P{N} есть правдоподобность утверждения Леверье «самого[250] по себе», т. е. без ссылки на истинность или ложность теории T; лежащее в основании состояние знаний то же, что и предположенное при оценке правдоподобности

362

P{T}. Это P{N} должно быть крайне мало: если мы игнорируем теорию Ньютона T, то какое основание мы могли бы иметь для подозрения, что существует за-урановая планета с такими-то и такими-то точными свойствами, столь близкая к данной точке неба?

Далее, P{N/T} есть правдоподобность утверждения Леверье N в свете вычислений Леверье, основанных на теории T, и, таким образом, это — понятие, очень отличное от P{N}. Возможно Леверье окончательно не показал, что существование за-урановой планеты с такими-то и такими-то свойствами является единственным объяснением, совместимым с теорией T. Однако он довольно близко подошел к тому, чтобы показать именно это и, таким образом, P{N/T}не может быть слишком далека от достоверности. Подводя итоги, мы можем рассматривать P{N/T} как довольно большую дробь, не очень отличающуюся от 1, а P{N} — как очень малую дробь, близкую к 0. но если мы так думаем, то отношение P{N/T}/P{N} кажется очень большим, и таким же должно казаться отношение P{T/N}/ P{T}, имеющее в силу написанного выше равенства то же самое значение, что и предыдущее отношение. Поэтому P{T/N}, наша уверенность в теории T после подтверждения предсказания Леверрье, кажется гораздо большей P{T}, нашей уверенности в той же теории до этого подтверждения.

(Предыдущее рассмотрение остается в рамках, которыми мы предусмотрительно ограничили себя в § 5. однако отбросим на время предосторожности и позволим себе несколько рискованных грубых оценок.

Предсказание Леверье N охватывает много деталей, из которых мы выберем только одну: новая планета будет близка к такой-то точке неба. Она была найдена фактически в пределах одного градуса от указанной точки (на расстоянии 52′). Однако вероятность того, что точка, выбранная наугад на сфере, окажется в пределах одного градуса от предложенной точки, может быть вычислена при простых допущениях, как мы установили выше, в (2). Мы находим, что P{N} значительно меньше, чем 0,00007615. Мы едва ли можем рассматривать P{N/T} как точно равную 1, но не без оснований мы можем думать, что, полагая

P{N} = 0,00007615, P{N/T} = 1,

Мы значительно больше переоцениваем скорее первую, чем вторую правдоподобность. И, таким образом, мы приходим к неравенству

Конечно, такая оценка сомнительна. Могут быть соображения аналогии, полностью независимые от теории Ньютона T, наталкивающие на мысль, что у новой планеты больше шансов быть ближе к плоскости земной орбиты, чем дальше от нее. Если мы так думаем, то вместо 0,00007615 мы должны были бы подставить бо́льшую дробь, но все же меньшую,

чем 1/180 = 0, 005556;

ср. (2).

Такие оценки можно было бы обсуждать бесконечно. Например, так как P{N/T}, разумеется, меньше, чем 1, то предложенное неравенство влечет за собой

P{T} < 0,00007615.

Нам может показаться соблазнительным увидеть в этом опровержение предложенного неравенства, как бы некоторое «reductio as absurdum». Действительно, теория Ньютона T могла бы в 1846 году, даже до открытия Нептуна, рассматриваться как неколебимо установленная и, таким образом кажется абсурдом приписывать T такую низкую правдоподобность. Я не думаю, однако, что таком случае мы обязаны рассматривать правдоподобность 10^–5 как низкую: мы могли бы думать, что логическая несомненность, которой мы приписываем правдоподобность 1, несравнимо больше, чем уверенность, с которой мы отно-

363

симся к наилучшим образом установленному индуктивному обобщению, правдоподобность которого мы могли бы даже рассматривать как бесконечно малую; ср. пример 8.

После всего этого мы можем счесть более безопасным возвратиться к точке зрения §§ 5—10, которой мы, в сущности, придерживались в (4). Представляйте себе качественно, какое влияние на вашу уверенность окажет изменение в той или иной компоненте ситуации, но не связывайте себя никакой количественной оценкой.

5. Правдоподобие и правдоподобность[143]. У нас может быть какое-нибудь предположение относительно вероятностей. Например, вы можете предположить, что игральная кость, которую вы держите в руках, является идеально честной, т. е., каждая ее грань имеет одну и ту же вероятность 1/6. Конечно, этому предположению трудно поверить. Или вы можете предположить, что каждая грань этой кости имеет вероятность между 0,16 и 0,17, что было бы более правдоподобно[251]. Предположение относительно вероятностей есть статистическая гипотеза. Часто случается, что мы имеем только два очевидных соперничающих предположения: «физическое» предположение Ф и статистическую гипотезу С, ср. § 14.9(7) и пример 14.33. В таком случае нас может серьезно интересовать P{С}, правдоподобность статистической гипотезы С.

Статистическая гипотеза С соответствующим образом испытывается статистическим наблюдением. Пусть E обозначает предсказание, состоящее в том, что статистическое наблюдение даст такой-то результат. Рассмотрим правдоподобность P{E/С} и допустим, что эта правдоподобность имеет числовое значение, равное вероятности того, что событие типа, предсказанного E, произойдет, вычисленной на основании статистической гипотезы С. Как мы видели в примере 4, некоторые (вполне естественные) допущения о взаимозаменяемости или симметрии (входящие в статистическую гипотезу С) могут даже заставить нас приравнять правдоподобность вероятности[252].

Эту правдоподобность, или вероятность, P{E/С}, как мы говорили в § 14.7(5), можно рассматривать с двух различных точек зрения, ср. также § 14.8(5). С одной стороны, P{E/С} есть вероятность события типа, предсказанного E, вычисленная на основании статистической гипотезы С. С другой стороны, если такое событие происходит и действительно наблюдается, то мы склонны думать, что С тем менее правдоподобна, чем меньше числовое значение P{E/С}, и по этой причине мы называем P{E/С} правдоподобием статистической гипотезы С, оцениваемым, принимая во внимание тот факт, что событие, предсказанное E, действительно произошло. Ср. § 14.7(5), так же, как и § 14.8(5)[253].

Теперь из примера 14.26 (2) следует, что

В этом равенстве P{E/С} является не только правдоподобностью, но и вероятностью и имеет определенное числовое значение. Однако P{С/E}, P{С} и P{E}, являются только правдоподобными и не предполагается, что они обладают определенными числовыми значениями[144]. В частности, и P{С}, и P{С/E} обозначают правдоподобность одной и той же статистической гипотезы С, но первая — до, а вторая — после наблюдения события, предсказанного E. Перепишем наше равенство в менее условной форме, подчеркивая один из аспектов P{С/E}:

Правдоподобность после события	=	Правдоподобие · Правдоподобность до события	.
		Правдоподобность события

364

Наблюдая событие, предсказанное E, мы сталкиваемся с необходимостью принять решение: должны ли мы отвергнуть статистическую гипотезу С и принять соперничающее физическое предположение Ф или что же мы должны сделать? Наше решение должно быть основано на самой последней информации и, следовательно, на P{С/E}, правдоподобности статистической гипотезы после наблюдения события. Одним из множителей этой правдоподобности P{С/E} является правдоподобие P{E/С}: оно, пожалуй, является наиболее важным множителем, потому что оно обладает числовым значением, вычисленным с помощью ясного и знакомого приема, но все же только множителем, не полным выражением этой правдоподобности.

Правдоподобие — важное указание, но оно еще не все. Статистик может благоразумно ограничить себя вычислением правдоподобия,но заказчик статистика поступит неблагоразумно, если не будет учитывать другие множители. Он должен тщательно взвесить P{С}, правдоподобность статистической гипотезы С до события; фактически, эту P{С} мы имеем в виду, когда говорим о том, насколько «подходящей» или «реалистичной» является гипотеза С; ср. пример 14.33

6. Попытка Лапласа связать индукцию с вероятностью. Мешок содержит черные и белые шары в неизвестной пропорции; последовательно вытащены и вновь опущены m белых и n черных шаров. Какова вероятность того, что m′ + n′ последующих вытаскиваний дадут m′ белых и n′ черных шаров?

Частный случай этой явно безобидной задачи о мешке и шарах можно интерпретировать как фундаментальную задачу об индуктивном умозаключении, сведенную к своему простейшему выражению. Действительно, рассмотрим случай, когда n = n′ = 0. Мы вытащили из мешка неизвестного состава m шаров, и все вытащенные шары оказались белыми. Мы можем уподобить эту ситуацию положению натуралиста, который испытал m следствий предположения и нашел, что все m наблюдений находятся в согласии с предположением. Натуралист планирует дополнительные наблюдения. Какова вероятность того, что следующие m′ наблюдений также окажутся в согласии с предположением? Этот вопрос можно истолковать как частный случай n = n′ = 0 предлагаемой задачи о мешке и шарах.

В этой задаче имеется темный и озадачивающий пункт: отношение числа черных шаров к числу белых шаров в мешке неизвестно. Однако если принять во внимание интерпретацию, которую мы имеем в виду, этот пункт представляется существенным[254]: натуралист не может знать «внутренний механизм» природы[255]. Он знает только то, что наблюдал, и мы знаем только то, что к этому моменту мешок дал столько-то белых шаров за столько-то высказываний[145].[256]

Здравый смысл, казалось бы, говорит нам, что мы не можем вычислить искомую вероятность, если ничего не известно о составе мешка: задача без достаточных данных неразрешимо. Однако Лаплас дал решение — спорное решение. Как ему вообще удалось подойти к решению?

Чтобы компенсировать недостаток данных, Лаплас вводит новый принцип; этот принцип спорен. «Когда вероятность простого события неизвестна, то можно предполагать ее равною всем числовым значениям от нуля до единицы», — говорит Лаплас[146]. «Это равное распределение незнания», — насмехаются его оппоненты.

Раз спорный принцип Лапласа принят, вывод решения непосредственен; нам нет необходимости его здесь рассматривать. Вот его результат: если m вытаскиваний дали только белые шары, то вероятность того, что m′ последующих вытаскиваний также дадут только белые шары, равна

365

Назовем это правило «Общим правилом последования». Наиболее известный частный случай относится к m′ = 1; если m вытаскиваний дали только белые шары, то вероятность того, что и следующее вытаскивание даст белый шар, равна

Назовем это «Специальным правилом последования»[147].

Приемлемы ли эти правила, если «белые шары» мы будем интерпретировать как «находящиеся в согласии наблюдения одной и той же природы», а «вероятность» — как «степень разумной уверенности»? Этот вопрос уместен, и мы его обсудим.

(1) Рассмотрим снова наш первый пример индуктивного рассуждения. Предположение Гольдбаха утверждает, что, начиная с 6 = 3 + 3, любое четное число является суммой двух простых нечетных чисел. Таблица в § 1.3 подтверждает это предположение для четных чисел до 30. Убедившись, что оно верно до 30, мы с большей или меньшей уверенностью ожидаем, что оно окажется верным и в следующем случае, для 32. специальное правило последования можно понимать как означающее следующее: после того как предположение Гольдбаха подтвердилось в первых m случаях, мы имеем право ожидать, что оно подтвердится в следующем случае с вероятностью

Разберемся в том, что это значит. Когда m возрастает, вероятность также возрастает; в самом деле, чем больше случаев подтвердилось в прошлом, тем более уверенно мы ожидаем, что предположение подтвердится в следующем случае. Если m стремится к ∞, то вероятность стремится к 1: накапливая все больше и больше подтверждений, мы могли бы надеяться все ближе и ближе подойти к достоверности. Рассмотрим теперь разность между двумя вероятностями, одна из которых соответствует m + 1, а другая m — предшествующим подтверждениям[257]:

[258]

Когда m возрастает, эта разность убывает: верно, что каждое новое подтверждение увеличивает нашу уверенность, но увеличивает все меньше и меньше, когда это подтверждение производится после все большего и большего числа предшествующих сходных подтверждений. (Сходство подтверждений в этом месте существенно[259]; ср. § 12.1.)

Перейдем теперь к Общему правилу последования. Его можно понимать как означающее следующее: после того как предположение Гольдбаха подтвердилось в первых m случаях, мы имеем право ожидать, что оно подтвердится в следующих m′ случаях с вероятностью

Если мы фиксируем m′, а m будем увеличивать, то эта вероятность будет убывать: в самом деле, чем дальше мы пытаемся предсказать будущее на основании прошлых наблюдений, тем менее уверенно мы его можем предсказать. Если m′ неограниченно возрастает, то m стремится к 0. в самом деле, подтверждение для всех значений m′ означало бы, что предположение Гольдбаха истинно. Очевидно, на основании данного числа m наблюдений мы не можем утверждать, что предположение истинно. Из этого правила, по-видимому, следует более сильное утверждение: на основании m наблюдений мы не можем даже приписать предпо-

366

ложению Гольдбаха вероятность отличную от нуля, и такое сильное утверждение может указывать верное направление.

(2) До этого момента Правило последования казалось довольно приемлемым. Но посмотрим на него более конкретно. Припишем m числовое значение и не будем игнорировать повседневных ситуаций. Будет достаточно рассмотреть Специальное правило последования.

Я испытал четные числа 6, 8, 10, …, 24 и нашел, что каждое из них есть сумма двух нечетных простых чисел. Правило говорит, что я должен был бы с вероятностью 11/12 ожидать, что и 26 является суммой двух нечетных простых чисел.

В иностранном городе, где я едва понимал язык, я питался в ресторане с большими опасениями. Однако после 10 посещений ресторана я не почувствовал никаких болезненных последствий и поэтому совершенно уверенно шел в ресторан одиннадцатый раз. Правило говорит, что вероятность того, что я не буду отравлен во время следующего посещения, равна 11/12[260].

Мальчику 10 лет. Правило говорит, что, прожив 10 лет, он имеет вероятность 11/12 прожить еще один год. Дедушка этого мальчика достиг 70 лет. Правило говорит, что он имеет вероятность 71/72 прожить еще один год.

Эти применения кажутся глупыми, но нет ничего глупее следующего применения, принадлежащего самому Лапласу. «Если отнести древнейшую историческую эпоху, — говорит он, — за пять тысяч лет, или за 1 826 213 дней назад и принять во внимание, что солнце постоянно восходило за этот промежуток времени при каждой смене суток, то будет 1 826 214 шансов против одного за то, что оно взойдет и завтра»[148]. Я, конечно остерегся бы предложить такое пари норвежскому коллеге, который мог бы для нас обоих устроить воздушное путешествие в какое-нибудь место за полярным кругом[261].

Однако правило может превзойти и эту нелепость. Применим его к случаю m = 0: вывод правила имеет такую же силу для этого случая, как и для всякого другого. Но для m = 0 правило утверждает, что любой предположение без какого бы то ни было подтверждения имеет вероятность ½. Каждый может придумать примеры, демонстрирующие чудовищность такого утверждения. (Кстати, оно и противоречиво.)[262]

(3) Наше обсуждение было длинным. Если бы мы выражались более осторожно, оно было бы еще более длинным и могло бы быть продолжено, но вот к чему оно сводится: правило последования может казаться мудрым, если мы избегаем числовых значений, но оно, несомненно, кажется глупым, если мы спускаемся до числовых значений. Пожалуй, оно указывает на мораль: в применениях исчисления вероятностей к правдоподобным рассуждениям принципиально избегайте числовых значений. Во всяком случае, именно эту точку зрения мы отстаиваем в этой главе.

7. Почему не количественно. Эта глава развивает тезис: исчисление вероятностей к правдоподобным рассуждениям применять следует, но только качественно. Но есть сильный соблазн применять его количественно и поэтому мы должны рассмотреть еще несколько связанных с этим вопросов.

(1) Несравнимы. Имеются некоторые доводы в пользу того, что предположение Гольдбаха относительно сумм двух нечетных простых чисел правильно; см. §§ 1.2, 1.3. Имеются некоторые доводы в пользу того, что древние скандинавы высаживались на американский материк задолго до Колумба. Какие доводы сильнее?

В самом деле, это, по-видимому, очень глупый вопрос. С какой целью могут сравнивать два таких совершенно различных случая? И кто должен был бы их сравнивать? Чтобы со знанием дела оценить эти доводы, вы должны были бы быть специалистом. В одном случае доводы должен был бы оценивать историк, специалист по древней истории Скандинавии. Едва ли найдется человек, который был бы специалистом и в той, и в другой области[263].

367

Как бы то ни было, наш явно глупый вопрос указывает одну возможность. Может случиться, то нет никакого разумного решения, никакого разумного способа сказать, какие доводы сильнее других[264]. Эта возможность так важна, что заслуживает специального термина. Если нет разумного способа решить, какие доводы сильнее, E₁ или E₂, то назовем E₁ несравнимыми с E₂. Мы могли бы в предыдущей главе найти несколько примеров, которые более ясно и более убедительно, чем пример, с которого мы здесь начали, наводят на мысль, что одни доводы могут быть не сравнимы[265] с другими[266]. См. § 4.8.[267]

(2) Сравнимы. После того как указано на возможность того, что доводы могут быть несравнимы, посмотрим несколько случаев, когда они очевидным образом сравнимы.

Пусть E₁ обозначает доводы в ползу предположения Гольдбаха (§ 1.2), возникающие в результате подтверждения его для всех четных чисел до 1000. пусть E₂ обозначает доводы в пользу того же предположения, возникающие в результате подтверждения его для четных чисел до 2000. очевидно, доводы E₂ сильнее, чем доводы E₁. теперь изменим обозначения и пусть E₁ обозначает существующие доводы в пользу высадки древних скандинавов на американский континент до Колумба. Пусть E₂ обозначает доводы, в которые превратились бы доводы E₁., если бы кто-либо открыл, скажем, где-нибудь на берегу Лабрадора, место захоронения, содержащее щиты и мечи, сходные со щитами и мечами, сохраняемыми где-нибудь со времен викингов. Очевидно, доводы E₂ были бы сильнее, чем доводы E₁.

Рассмотрим еще одинн, несколько более тонкий случай. Пусть теперь E₁ обозначает доводы в пользу предположения A, возникающие в результате подтверждения одного из его[268] следствий B. После того как следствие B подтвердилось, кто-нибудь замечает, что B само по себе очень невероятно[269]. (Это замечание могло бы быть вполне точным; вероятность B, вычисленная на основании простой и явно подходящей статистической гипотезы, могла бы быть очень мала.) Это замечание изменяет доводы E₁ в пользу предположения A в доводы E₂. Доводы E₂ сильнее, чем доводы E₁. (Мы это уже говорили, возможно, немножко менее четко, в § 12.3.)

Во всех трех примерах мы получили доводы E₂ из доводов E₁, прибавляя какое-либо уместное наблюдение. Однако если между E₁ и E₂ нет такой простой связи, то как мы сможем решить, какие доводы сильнее? Этот вопрос делает еще более очевидной возможность того, что доводы могут быть несравнимы.

(3) Сравнимы, но все же не количественно. В предыдущем пункте (2) мы встретили случаи, когда доводы E₂ можно разумно считать более сильными, чем доводы E₁. Но насколько более сильными? Мне кажется, что на этот вопрос ни в одном из предыдущих случаев нет никакого разумного ответа. И, таким образом, мы все же остаемся на качественном уровне.

(4) Как бы это выглядело? В § 4 мы начали с того, что взяли символ P{A} для обозначения правдоподобности предположения A. В последующих параграфах этой главы мы пытались справиться со своей задачей, не придавая P{A} никакого определенного числового значения: в этом состоит «качественная точка зрения, которую отстаивает эта книга. «Количественная точка зрения состояла бы в том, чтобы придавать P{A} определенное числовое значение всякий раз, когда исчисление вероятностей применяется к правдоподобным рассуждением относительно предположения A.

Тяжесть доказательства всецело ложится на тех, кто защищает количественные приложения теории вероятностей к правдоподобным рассуждениям. От них требуется только получить класс нетривиальных предположений A, для которых правдоподобность P{A} может быть вычислена с помощью ясного метода, по крайней мере в нескольких случаях приводящего к приемлемым результатам[149].

368

Никто еще не предложил ясного и убедительного метода вычисления правдоподобностей в нетривиальных случаях, и если мы ясно представим конкретные ситуации, в которых важна правильная оценка правдоподобностей (что мы уже сделали), то мы легко сможем понять, что любое приписывание правдоподобностям определенных числовых значений подвергается большой опасности показаться глупым.

Правдоподобности, имеющие определенные числовые значения, сравнимы: два числа или равны, или одно из них больше другого. Однако после обсуждения в (1) и (2) нам будет трудно допустить, что любые два предположения должны быть сравнимы по правдоподобности. Возьмите два предположения, с которых мы начали обсуждение: предположение Гольдбаха и упомянутое относящееся к истории предположение относительно открытия Америки. Если бы мы приписали их правдоподобностям числовые значения. То силу доводов, говорящих в пользу одного из них, можно было бы сравнить с силой доводов, говорящих в пользу другого, однако такое сравнение кажется бесполезное и глупым.

(5) Стоит ли? Есть другой вопрос, не зависящий от предыдущего обсуждения, который следует рассмотреть. Вес правдоподобной аргументации может быть крайне важен, но эта важность является условной, недолговечной, переходящей: стоит ли связывать числовое значение с чем-то столь недолговечным. Какова правдоподобность закона тяготения Ньютона, если судить по фактам, собранным в первом издании Начал? Вообразим на минуту, что существует метод, позволяющий численно оценить такую правдоподобность. Однако мы не должны ни на минуту воображать, что эта оценка может быть легкой: ввиду сложности фактов и их взаимоотношений оценка должна быть тонкой, а вычисления длинными. Стоит ли ее предпринимать? Возможно, стоило бы для нас ввиду исторический и философской важности открытия Ньютона. Но едва ли для Ньютона и его современников: вместо вычисления правдоподобности этой теории они при таких же усилиях могли бы изменить эту правдоподобность, развивая теорию и умножая наблюдения. Кажется нелепым посвятить десять лет вычислению степени правдоподобности, которая имеет силу только одну секунду.

8. Бесконечно малые правдоподобности? Подтвердился новый частный случай какого-нибудь теоретико-числового предположения (например, предположения Гольдбаха; ср. §§ 1.2, 1.3). Такое подтверждение следует рассматривать как повышающее вес доводов, или правдоподобность этого предположения. Но никакое количество таких подтверждений не может доказать предположение. Возможно, мы даже чувствуем, что никакое количество таких подтверждений не может заметно приблизить предположение к доказательству. [Ср. примеры 4(5), 6(1).] Такие чувства могут навести на мысль ввести бесконечно малые в исчисление вероятностей.

Современной математикой бесконечно малые могут трактоваться совершенно ясно. Мы рассматриваем «величины» a, b, …, представленные «формальными степенными рядами»:

a = a₀ + a₁ε + a₂ε² + a₃ε³ + …;

Мы говорим, что a положительно, если первое неравное нулю число в последовательности a₀, a₁, a₂,… положительно. Из этого определения легко выводим два основных правила:

Или a = 0 или a положительно или — a положительно и эти три возможности являются взаимно исключающими.

Сумма и произведение двух положительных величин положительны.

369

Мы говорим, что a > b, если a — b положительно. Из этих определений следует, что любое положительное число больше, чем ε (т. е. больше, чем формальный степенной ряд 0 + ε + 0 · + 0 · ε² + 0 · ε³ + …), хотя ε² положительно. И, таким образом, ε есть «актуальная» бесконечно малая.

Мы могли бы теперь рассмотреть некоторую форму исчисления вероятностей, в которой вероятности (или правдоподобности) не являются необходимо числами, но величинами a только что описанного вида, подчиняющимися условию 0 ≤ a ≤ 1. В таком исчислении правдоподобность предположения Гольдбаха после 1 000 000 или любого другого числа подтверждений могла бы все еще быть бесконечно малой, т. е. величиной a с a₀ = 0.

Я воздерживаюсь от комментариев в отношении перспектив такого плана. Как бы то ни было, он открывает возможность рассматривать нечисловые правдоподобности под другим углом зрения.

9. Правила допустимости. Я желаю, чтобы читатель вывел свои собственные заключения и сформировал свое собственное мнение. Поэтому я отложил выражение своего мнения на критический вопрос до этого последнего примечания к главе. Я имею в виду вопрос, поставленный первым параграфом этой главы: существуют ли для правдоподобных рассуждений правила какого-либо типа?

Довольно очевидно, что правдоподобные рассуждения не имеют правил того же типа, что и доказательные рассуждения. Пусть нам предложено доказательство. Если оно расчленено на достаточно малые шаги, то правильность каждого шага может быть проверена с помощью правил формальной логики[150]. Если все шаги соответствуют этим правила, то доказательство верно, но оно неверно, если есть шаг, нарушающий правила. Таким образом, правила доказательной логики являются решающими: они могут решить, является ли предложенное доказательное рассуждение обязательным или нет. Схемы правдоподобных рассуждений, которые мы собрали, таких функций выполнять не могут. Пусть нам предложено правдоподобное рассуждение. Каждый его шаг имеет целью сделать более правдоподобным некоторое предположение, и он[270] это осуществляет, следуя какой-нибудь принятой схеме. Проследив каждый шаг всего этого рассуждения, вы не обязаны в какой-нибудь определенной степени полагаться на это предположение.

Однако существуют правила различных типов. Логические правила очень отличаются от судебных правил. Суду следует выслушать все заинтересованные стороны, но он не обязан прислушиваться к тому, что не имеет отношения к делу. Поэтому суд должен иметь власть исключать из своего рассмотрения все, не относящееся к делу, и такая власть регулируется правилами допустимости. Без каких-либо правил такого типа не могло бы быть никакого организованного отправления правосудия: суд не мог бы ограничить беспринципного адвоката, который с помощью нечестных и не относящихся к делу вопросов мог бы постепенно измотать неблагоприятных свидетелей, противную сторону, присяжных и судью или беспредельно затянуть процесс[271].

Схемы правдоподобных рассуждений, собранные в предыдущих главах, могут рассматриваться как правила допустимости в научной дискуссии. Вы никоим образом не обязаны придавать предположению определенную степень веры, если подтвердились какие-либо из его следствий. Однако во время обсуждения этого предположения, несомненно, допустимо упомянуть такие подтверждения и будет честным и разумным к ним прислушаться. Наши схемы отмечают различные обстоятельства, относящиеся к таким подтверждения, которые могли бы оказать разумное влияние на вес доводов (как аналогия или отсутствие аналогии с предыдущими подтверждениями и т. д.). Будет честным и разумным допустить обсуждение и таких обстоятельств. Когда автор собирал эти схемы, его намерение состояло в том, чтобы записать те общие обстоятельства, которые в соответствии с обычаями хороших ученых допустимы в научной дискуссии и

370

имеют целью оказать разумное влияние на правдоподобность обсуждаемого предположения.

В суде присяжных власть суда разделена между присяжными и председательствующим судьей. Это разделение власти (как оно понимается некоторыми юридическими авторитетами и в какой-то степени принято судебной практикой некоторых штатов и стран) представляет для нас большой интерес. Присяжные и судья имеют различные функции, они решают различные вопросы. На вопросы, касающиеся допустимости доводов, отвечает судья, на вопросы, касающиеся правдоподобности допущенных доводов, отвечают присяжные. Дело судьи решить, какие доводы заслуживают рассмотрения присяжных. Дело присяжных определить, имеют ли представленные на рассмотрение доводы достаточный вес. При решении, что заслуживает рассмотрения присяжных, а что нет, судья должен знать и уважать прецеденты, судебные обычаи и формулированные правила допустимости. При взвешивании представленных доводов присяжный, возможно, не имеющий вообще никакой юридической подготовки, должен полагаться на свой собственный здравый смысл.

Короче говоря, власть суда так делится между судьей и присяжными, как власть оценки рассматриваемого предположения в каждом из нас делится между объективными правилами и субъективным здравым смыслом. Судья играет роль правил, присяжные — роль вашей личной проницательности. Дело объективных правил правдоподобных рассуждений решить, какого рода доводы заслуживают рассмотрения. Однако дело вашего субъективного здравого смысла решить, имеют ли только что представленные конкретные доводы достаточных вес или нет[151]

XVI. ПРАВДОПОДОБНЫЕ РАССУЖДЕНИЯ В ИЗОБРЕТЕНИИ И ОБУЧЕНИИ

Слова состоят из букв алфавита, предложения из слов, которые можно найти в словаре, и книги из предложений, которые можно найти и у других авторов. Однако если то, что я говорю, содержательно и связано таким образом, что следует одно из другого, то вы столь же можете порицать меня за заимствование моих предложений у других, сколь и за заимствование моих слов у словаря. — Декарт[152]

1. Предмет настоящей главы. Примеры в первой части этого труда и рассмотрения предыдущих глав второй части, я надеюсь, проливают некоторый свет на роль правдоподобных рассуждений в открытии математических фактов. Но математик не только догадывается; он должен также решать задачи и должен доказывать факты, о которых он догадался. Какова роль правдоподобных рассуждений в открытии решения или в изобретении доказательства? Вот вопрос, который будет рассмотрен в настоящей главе. И вот, между прочим, вопрос, привлекший внимание автора, который, первоначально интересуясь методами решения задач, в конечном счете пришел к теме настоящей книги.

Правдоподобные рассуждения являются темой тонкой и неуловимой, и такой же темой являются методы решения. Пожалуй, было правильно отложить вопрос, объединяющий две такие деликатные темы, до последней главы. Последующее рассмотрение будет кратким; главная цель — указать связь с ранее обсуждавшимися вопросами. Более пространное изложение подошло бы для другой книги о методах решения задач.

2. Рассказ о маленьком открытии. Решение любой простой, но не совсем стандартной математической задачи может потребовать некоторого напряжения и доставить вам триумф открытия. Рассмотрим следующий пример: Построить четырехугольник, если даны его четыре стороны a, b, c и d и угол φ, образованный противоположными сторонами a и c.

Данные задачи показаны на рис. 16.1: четыре отрезка и один угол, обломки фигуры, разорванной на части, которые мы должны воссоединить, чтобы удовлетворить всем требованиям, предписанным в задаче.

372

Подразумевается, что стороны a, b, c и d следуют одна за другой вокруг искомого четырехугольника в этом порядке, так что a противоположна c, а b противоположна d. Угол φ, образованный противоположными сторонами a к c, не является ни одним из четырех углов четырехугольника.

Зададим несколько обычных вопросов, которые могут приблизить к нам задачу.

Достаточно ли данных для определения неизвестного? Одних четырех сторон было бы, очевидно, недостаточно для определения четырехугольника: четыре палки, соединенные гибкими шарнирами в их соответствующих концах, образуют четырехугольник, который способен двигаться, деформироваться, не является жестким, не имеет определенной формы. Однако, если один из его четырех углов фиксирован, шарнирный четырехугольник не может больше двигаться: четырехугольник определяется четырьмя своими сторонами и одним из своих углов. Мы можем догадаться, что он определяется также четырьмя сторонами и каким-нибудь другим углом, и, таким образом, данные нашей задачи кажутся достаточными.

Рис. 16.1. Обломки.	Рис. 16.2. Холодно.

Сделайте рисунок. Мы чертим рис. 16.2, на котором изображены все пять данных, соединенных так, как они должны были бы быть соединены в соответствии с условиями предложенной задачи. По-видимому, мы должны воспользоваться всеми данными.

Может случиться, что в этом месте мы застрянем, и в течение известного времени нам в голову не придет никакой полезной идеи. Действительно, рис. 16.2 выглядит неуклюжим. Стороны a, b, c, d находятся, конечно, на своих правильных местах, но положение угла φ кажется неудачным. Этот угол — одно из наших данных, мы должны им воспользоваться. Но как мы можем им воспользоваться, если он расположен так далеко, в таком необычном месте?

Человек, имеющий опыт в решении задач, попытался бы переделать рисунок, он попытался бы поместить этот угол φ где-нибудь в другом месте. Он может, таким образом, напасть на мысль начертить рис. 16.3, где угол φ образован стороной a и параллелью к стороне c, проведенной через конец стороны a. Рис. 16.3 выглядит более многообещающим, чем никчемный рис. 16.2.

373

Но почему же рис. 16.3 кажется многообещающим? Даже хорошие студенты, довольно уверенно это чувствующие, могут не суметь ясно ответить на такой вопрос.

«Он мне кажется хорошим».

«Данные расположены более компактно».

Только студент, исключительно одаренный или опытный, будет в состоянии дать полное объяснение: «На рис. 16.2 угол φ входит в треугольник, однако этот треугольник не годится для построения: у него известны только угол φ и сторона b. А вот если угол φ расположен как на рис. 16.3, то он имеет больше шансов войти в подходящий треугольник. Это желательно, так как обычно построение такого рода сводится к построению треугольника по подходящим данным».

Рис. 16.3. Теплее.

Последний ответ указывает, по-видимому, на общую идею: многообещающей кажется любая черта, в отношении которой можно обнаружить, что нынешняя ситуация находится в согласии с удачными ранее встречавшимися ситуациями.

Как бы то ни было, рис. 16.3 оправдывает наши ожидания. В самом деле, угол φ действительно входит в треугольник, который мы легко можем построить (по сторонам a и c и углу φ между ними, см. рис. 16.4). Когда построен этот треугольник, решение совсем близко. В самом деле, к только что построенному треугольнику примыкает другой треугольник, который мы можем построить (по сторонам b, d и ранее построенной стороне, см. рис. 16.5). Начертив оба треугольника, мы завершаем требуемое построение, строя параллелограмм со сторонами b и с.

Рис. 16.4. Жарко!	Рис. 16.5. Сделано!

Для большинства людей, решающих задачи, главным шагом в предыдущем решении, изображенном последовательностью из пяти рисунков, является переход от рис. 16.2 к рис. 16.3; этому шагу может

374

предшествовать длительный период колебаний. Но как только угол φ расположен удачно, развитие решения от рис. 16.3 через рис. 16.4 к заключительному рис. 16.5 может быть очень быстрым.

Предыдущее решение может выявить один или два момента, играющих известную роль и в более важных открытиях.

3. Процесс решения. Решение задачи — крайне сложный процесс. Никакое описание или теория этого процесса не может исчерпать многообразия его сторон, любое его описание или теория обязательно являются неполными, схематичными, чрезвычайно упрощенными. Я хочу указать место правдоподобных рассуждений в этом сложном процессе и выберу наиболее простое описание, какое я в состоянии найти, в котором это место может быть опознано. И здесь будет достаточно даже начала такого простого описания.

(1) Постановка задачи для себя. Задача становится задачей для вас, когда вы ставите себе целью ее решить. Задача еще не является вашей задачей только потому, что вам на экзамене предложено ее решить. Если вы хотите, чтобы кто-нибудь пришел и подсказал вам ответ, то я подозреваю, что вы еще не поставили себе эту задачу всерьез. Но если вам очень хочется найти ответ самому, своими собственными силами, то вы сделали задачу действительно вашей, вы относитесь к ней серьезно.

Постановка задачи для себя есть начало решения, существенный первый ход в игре, означающий решимость взяться за задачу.

(2) Избирательное внимание. Вам не нужно мне говорить, что вы поставили себе эту задачу, вам не нужно говорить это себе самому; что вы это сделали, покажет все ваше поведение. Ваш ум становится избирательным; он становится более доступным для всего того, что выглядит связанным с задачей, и менее доступным для всего, что кажется несвязанным. Вы энергично ухватываетесь за любое воспоминание, замечание, намек или факт, который мог бы помочь вам решить вашу задачу, и закрываете дверь для всего другого. Когда дверь закрыта так плотно, что вас не достигают даже наиболее настоятельные призывы внешнего мира, люди говорят, что вы поглощены задачей.

(3) Регистрирование темпа продвижения. Есть и другое обстоятельство, показывающее, что вы серьезно заняты своей задачей; вы становитесь чувствительны. Вы остро чувствуете темп вашего продвижения; у вас поднимается настроение, когда он быстр, вы приходите в уныние, когда он медленен. Обо всем, что бы ни пришло вам на ум, вы быстро составляете мнение: «Это выглядит неплохо», «Это могло бы помочь» или «Плохо», «Не поможет». Такие суждения, конечно, не безошибочны. (Хотя, по-видимому, они чаще правильны, чем нет, особенно у одаренных или опытных людей.) Как бы то ни было, такие суждения и чувства для вас лично важны; они направляют ваши усилия.

375

(4) Где появляются правдоподобные рассуждения. Несколько более конкретно рассмотрим типичную ситуацию.

Вы пытаетесь добиться решения в известном направлении, на определенном пути. (Например, пытаясь решить геометрическую задачу из § 2, вы отказываетесь от рис. 16.2 и пробуете работать с более обнадеживающим рис. 16.3.) Вы можете очень остро чувствовать, что движетесь в правильном направлении, что вы на многообещающем пути, что вы идете по следу. Между прочим, вы можете это чувствовать, не формулируя свое чувство словами. Или, даже если вы говорите что-нибудь вроде «Это выглядит неплохо», вы не делаете усилий, чтобы проанализировать свою уверенность, вы не спрашиваете «Почему это выглядит неплохо?». Вы просто слишком заняты, идя по следу.

Однако вам может не повезти. Вы наталкиваетесь на трудности, у вас нет больше продвижения, ничего нового не приходит в голову, и тогда вы начинаете сомневаться: «Было ли это хорошим началом? Правильное ли это направление?» А затем вы можете начать анализировать свое чувство: «Направление казалось вполне правдоподобным — но почему оно правдоподобно?» Затем вы можете приняться обдумывать ситуацию, и вам в голову могут прийти какие-нибудь более ясные соображения:

«Эта ситуация не так уж плоха. Я могу ввести треугольник. В подобных задачах всегда вводят треугольники».

«В конце концов, это было, вероятно, правильное начало. Похоже на то, что это правильное решение. Что мне нужно для решения задачи этого типа? Вот это и это у меня есть. А это? И это есть. А...»

Было бы интересно более отчетливо понять, как люди рассуждают в такой ситуации, в действительности наша главная цель и состоит именно в том, чтобы это понять. Однако, чтобы расширить базу наших наблюдений, нам нужен по крайней мере еще один пример.

4. Deus ex machina[153][154]. Следующий пример немножко менее прост, чем пример из § 2. Он будет дан в § 6 после некоторых приготовлений в этом параграфе и в следующем.Параграф 6 доставит нам доказательство, изложенное таким способом, который находится в контрасте с обычным способом изложения. Чтобы подчеркнуть этот контраст, сначала рассмотрим это доказательство, как оно было бы изложено в (рассчитанном на более подготовленных читателей) учебнике или в математическом журнале.

376

Математическая книга или лекция прежде всего должна быть правильной и недвусмысленной. Тем не менее мы знаем по тяжелому опыту, что совершенно недвусмысленное и правильное изложение может быть далеким от удовлетворительного и может казаться невдохновляющим, утомительным или разочаровывающим, даже если излагаемый вопрос сам по себе интересен. Наиболее бросающийся в глаза недостаток в остальном приемлемого изложения есть «deus ex machina». Перед дальнейшими замечаниями я хочу привести конкретный пример. Взглянем на доказательство следующей, не совсем элементарной теоремы[155].

Если члены последовательности a₁, a₂, a₃, ... — неотрицательные действительные числа, не все равные 0, то

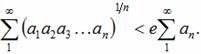
Доказательство. Определим числа c₁, c₂, c₃, ... равенствами

c₁c₂c₃ ... c_n = (n + 1)ⁿ

для n=1, 2, 3, ... Мы пользуемся этим определением, затем неравенством между средним арифметическим и средним геометрическим и, наконец, тем фактом, что последовательность с общим членом [(k+1)/k]^k, определяющая e, является возрастающей. Получаем

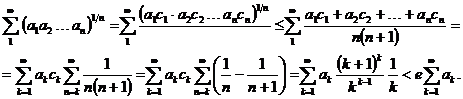(d)

377

5. Эвристическое оправдание. Критический пункт вывода (d) — определение последовательности c₁, c₂, c₃, ... Этот пункт с самого начала, без какой-либо подготовки, кажется правильным, как типичный «deus ex machina». Каковы возражения против него?

«Он кажется кроликом, вытащенным из шляпы».

«Он внезапно появляется из ничего. Он выглядит таким произвольным. Он не имеет никакой видимой мотивировки или цели».

«Я терпеть не могу ходить в темноте. Я терпеть не могу делать шаг, когда не вижу, почему бы он должен был подвести меня ближе к цели».

«Возможно, автор знает цель этого шага, но я ее не знаю, и потому не могу следовать за ним с доверием».

«Послушайте, я здесь не для того, чтобы только восхищаться вами. Я хочу научиться, как самому решать задачи. Но я не могу понять, как человек мог напасть на ваше … определение. Так чему же я могу здесь научиться? Как смог бы я найти такое … определение сам?»

«Этот шаг не тривиален. Он кажется решающим. Если бы я мог видеть, что он имеет известные шансы на успех, или увидеть для него какое-нибудь предварительное правдоподобное оправдание, то я смог бы представить себе и как он был придуман и, во всяком случае, мог бы следовать за дальнейшим рассуждением с бóльшим доверием и с бóльшим пониманием».

Первые ответы не очень ясны, следующие лучше, а последний — самый лучший. Обнаруживается, что разумный читатель или слушатель желает две вещи:

Во-первых; понять, что настоящий шаг рассуждения является правильным.

Во-вторых, понять, что настоящий шаг является подходящим.

Шаг математического рассуждения является подходящим, если он существенно связан с целью рассуждения или если он подводит нас ближе к цели. Недостаточно, однако, чтобы шаг был подходящим: нужно, чтобы, он казался таким читателю. Если шаг простой, совсем тривиальный, обычный шаг, то читатель легко сумеет себе представить, как он мог бы быть связан с целью рассуждения. Если порядок изложения тщательно спланирован, то на мысль о связи этого шага с целью может наталкивать контекст. Если, однако, шаг явно важен, но его связь с целью вообще не видна, то он появляется, как «deus ex machina», и можно понять, что разумный читатель или слушатель разочарован.

В нашем примере определение c_n появляется, как «deus ex machina». Но этот шаг является несомненно подходящим. Действительно, рассуждение, основанное на этом определении, доказывает нашу теорему, и доказывает ее довольно быстро и ясно. Трудность состоит в том, что рассматриваемый шаг, хотя в конце и оправдывается, не кажется оправданным сначала.

378

Но как автор мог бы оправдать его с самого начала? Полное оправдание требует некоторого времени; оно дается полным доказательством. Что нужно — это не полное, а неполное оправдание, правдоподобный предварительный довод, просто намек, что этот шаг имеет некоторые шансы на успех, короче, некоторое эвристическое оправдание.

6. Рассказ о другом открытии. Почти нет необходимости напоминать читателю, что лучшие рассказы не представляют правды в чистом виде. Они должны, однако, содержать некоторые существенные элементы правды, в противном случае они не были бы даже хорошими. Нижеследующее является несколько «рационализированным» изложением шагов, которые привели меня к доказательству, изложенному в § 4; иными словами, в нем должным образом подчеркивается эвристическое оправдание последовательных шагов.

Теорема, доказанная в § 4, сама по себе удивительна. Мы удивлялись бы меньше, если бы знали, как она была открыта. Мы естественно приходим к ней, пытаясь доказать теорему: Если ряд с положительными членами

a₁ + a₂ + a₃ + ... + a_n + ...

сходится, то и ряд

a₁ + (a₁a₂)^1/2 + (a₁a₂a₃)^1/3 + ... + (a₁a₂a₃...a_n)^1/n + ...

также сходится. Я попытаюсь подчеркнуть некоторые соображения, которые могут нам помочь найти доказательство.

(1) Подходящая известная теорема. Естественно начать с обычных вопросов.

В чем состоит посылка? Мы допускаем, что ряд ∑ a_n сходится, что его частные суммы остаются ограниченными, что

a₁ + a₂ + ... + a_n   не велико.

В чем состоит заключение? Мы хотим доказать, что сходится ряд ∑ (a₁a₂...a_n)^1/n, что

(a₁a₂...a_n)^1/n малó.

Знаете ли вы теорему, которая могла бы оказаться полезной? Что нам нужно — это какая-нибудь связь между суммой n положительных величин и их средним геометрическим. Встречали ли мы ранее что-нибудь в этом роде? Если вы когда-нибудь слышали о неравенстве между средним арифметическим и средним геометрическим, то довольно велика вероятность, что вам придет на ум эта связь:

379

Это неравенство показывает, что (a₁a₂...a_n)^1/n малó, когда a₁ + a₂ + ... + a_n не велико. Оно имеет так много точек соприкосновения с нашей задачей, что мы едва ли сможем устоять от искушения его применить:

— полная неудача! Ряд ∑ (1/n) расходится, последнее выражение в (a) не имеет смысла.

(2) Учиться на неудаче. Трудно допустить, чтобы наш план был ошибочным. Хотелось бы верить, что по крайней мере некоторая его часть правильна. Вот полезные вопросы:Что в нашем плане было ошибочно? Какую его часть мы могли бы спасти?

Ряд a₁ + a₂ + ... + a_n + ... сходится. Следовательно, когда n велико, a_n малó. Но когда не все a₁, a₂, ..., a_n равны, две части неравенства (a.-g.) различны, и когда a₁, a₂, ..., a_n очень неравны, они могут быть очень различны. В нашем случае a₁ намного больше, чем a_n, и, таким образом, между двумя частями (a.-g.) может существовать значительный разрыв. Вот, вероятно, причина, по которой наше применение неравенства (a.-g.) оказалось недостаточным.

(3) Видоизменение подхода. Ошибка состояла в применении неравенства (a.-g.) к величинам

a₁, a₂, a₃, ..., a_n,

которые были слишком неравны. Так почему бы не применить его к каким-нибудь родственным величинам, которые имеют больше шансов быть равными? Мы могли бы испытать

1a₁, 2a₂, 3a₃, ..., na_n.

Быть может это идея! Мы можем ввести возрастающие компенсирующие множители, например 1, 2, 3, ..., n. Нам не следует, однако, связывать себя больше, чем это необходимо, стоило бы сохранить себе некоторую свободу действий. Нужно, пожалуй, рассмотреть с большей общностью величины

1^λa₁, 2^λa₂, 3^λa₃, ..., n^λa_n.

Можно было бы λ оставить на время неопределенным и выбрать наиболее выгодное значение позже. Этот план имеет столько

380

хороших черт, что кажется созревшим для исполнения:

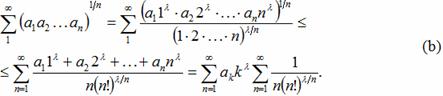
Мы натолкнулись на трудное место. Оценить последнюю сумму мы не можем. Даже если мы вспомним различные приемы, имеющие отношение к данному случаю, то все же будем вынуждены работать с «сырыми равенствами» (обозначение ≈, вместо =):

Вводя это в последнюю сумму формулы (b), мы очень близко подходим к доказательству того, что

где C — некоторая постоянная, возможно e^λ/λ^–1. Такое неравенство, конечно, доказало бы теорему, которую мы имеем в виду.

(4) Вновь просматривая предыдущее рассуждение, мы вынуждены повторить вопрос: «Какое значение λ наиболее выгодно?» Вероятно, то λ, которое делает e^λ/λ^–1 наименьшим. Мы можем найти это значение с помощью дифференциального исчисления:

λ = 1.

Это определенно наводит на мысль, что наиболее очевидный выбор и наиболее выгоден: в качестве компенсирующего множителя при a_n нужно взять n¹ = n или какое-нибудь число, не очень отличающееся от n, когда n велико. Это может привести в (b') к простому значению C = e.

(5) Больше гибкости. В нашем предыдущем рассуждении (b) мы оставили λ неопределенным. Это придало нашему плану известную гибкость: значение λ оставалось в нашем распоряжении. Почему бы не придать нашему плану еще большую гибкость? Мы могли бы оставить компенсирующий множитель при a_n совсем неопределенным; обозначим его буквой c_n и распорядимся его значением позднее, когда яснее увидим, что нам нужно. Перейдем к этой дальнейшей модификации нашего первоначального подхода:

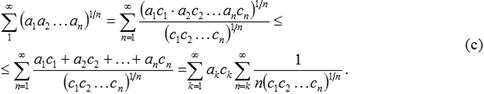
Как нам следовало бы выбрать c_n? Это — решающий вопрос, и мы больше не можем откладывать ответ.

Во-первых, мы легко видим, что множитель пропорциональности должен оставаться произвольным. Действительно, последовательность cc₁, cc₂, ..., cc_n, ... приводит к тем же результатам, что и c₁, c₂, ..., c_n, ...

Во-вторых, наша предшествующая работа наводит на мысль, что и c_n и (c₁c₂...c_n)^1/n должны были бы быть асимптотически пропорциональны n:

c_n ~ Kn, (c₁c₂ … c_n)^1/n ~ e^–1 Kn = K′n

В-третьих, больше всего желательно, чтобы мы были в состоянии найти сумму ряда

В этом месте нам понадобятся все наши знания о простых рядах. Если мы знакомы с рядом

то велика вероятность, что в этой связи мы о нем вспомним. Этот ряд обладает тем свойством, что его сумма имеет простое выражение не только от n = 1 до n = ∞, но и от n = k доn = ∞, — очень большое преимущество! Этот ряд подсказывает выбор

c₁c₂ ... c_n = (n + 1)ⁿ

Теперь, очевидно, n + 1 ~ n для большого n — хороший признак! А как обстоит дело с самими c_n?

382

Поскольку

c₁c₂ ... c_n–1c_n = (n + 1)ⁿ, c₁c₂ ... c_n–1 = n^n–1,

асимптотическая пропорциональность n является хорошим признаком! И возникает число e — очень хороший признак!

Мы выбираем эти c_n, и после этого выбора снова возвращаемся к выводу (d) в § 4 с бóльшим доверием, чем прежде.

Теперь мы можем понять, как человек мог открыть то определение c_n, которое появилось в § 4 как «deus ex machina». Вывод (d) также становится более понятным. Он выступает теперь в качестве последней и единственной успешной попытки в цепи последовательных испытаний (a), (b), (c) и (d). И объясняется само происхождение теоремы. Мы понимаем теперь, каким образом можно было открыть роль числа e, которая сначала казалась такой удивительной.

7. Несколько типичных указаний. Мы рассмотрели в предыдущих параграфах два примера. Сначала мы исследовали «задачу на нахождение» (в § 2), а затем «задачу на доказательство» (в § 6)[156]. Чтобы должным образом проиллюстрировать роль правдоподобных рассуждений в изобретении плана решения, нужно было бы значительно большее разнообразие примеров. Как бы то ни было, из наших примеров мы можем извлечь несколько типичных указаний, позволяющих оценивать план. Имея дело с другими указаниями такого рода, мы будем апеллировать ко всему тому опыту, который читатель приобрел в решении математических задач.

Перечисляя такие оценивающие указания, мы не будем пытаться добиться полноты. В некоторых случаях мы будем находить необходимым делать различие между задачами на нахождение и задачами на доказательство. В таких случаях мы будем давать две параллельные формулировки и первой давать формулировку, относящуюся к задачам на нахождение.

Рассмотрим ситуацию, в которой человек, решающий задачу, естественно сталкивается с правдоподобным рассуждением. Вы заняты интересной задачей. Вы задумали план решения, но почему-то он вам не очень нравится. У вас есть сомнения, вы не совсем уверены, что ваш план осуществим. Обдумывая это, вы фактически исследуете предположение:

A. Этот план решения можно осуществить.

Когда вы исследуете ваш план под различными углами зрения, вам может прийти на ум несколько за и против. Вот некоторые бросающиеся в глаза типичные указания, которые могут говорить в пользу предположения A.

383

B₁. Этот план принимает в расчет все данные.

Эта формулировка относится к задачам на нахождение. Имеется параллельная формулировка, относящаяся к задачам на доказательство: этот план принимает в расчет все части посылки. Например, рис. 16.3 соединяет все данные, и это хороший признак. И рис. 16.2 содержит все данные, но между этими двумя фигурами существует различие, которое могут сделать ясным следующие пункты.

B₂. Этот план обеспечивает связь между данными и неизвестным.

Имеется параллельная формулировка, относящаяся к задачам на доказательство: этот план обеспечивает связь между посылкой и заключением. Например, в § 6 (1) неравенство между средним арифметическим и средним геометрическим обещало создать связь между посылкой и заключением, и такое обещание побуждает нас работать с этим неравенством. Рис. 16.3, по-видимому, обеспечивает более тесную связь, и поэтому кажется более многообещающим, чем рис. 16.2.

B₃. Этот план имеет черты, часто оказывающиеся полезными при решении задач такого типа.

Например, план, начинающийся с рис. 16.3, на более позднем этапе (рис. 16.4) приводит к построению треугольника. Это хороший признак, так как задачи на геометрические построения часто сводятся к построению треугольников.

B₄. Этот план похож на план, с помощью которого удалось решить аналогичную задачу.

B₅. С помощью этого плана удалось решить задачи в частном случае.

Например, у вас есть план для решения трудной задачи, относящейся к произвольной замкнутой кривой. Прямое проведение этого плана, по-видимому, требует большой работы, и поэтому вы колеблетесь. Однако вы замечаете, что в частном случае, когда замкнутая кривая есть окружность, ваш план осуществляется и дает правильный результат. Это хороший признак, и вы чувствуете себя ободренным.

B₆. С помощью этого плана удалось решить часть задачи (найти некоторые из неизвестных или доказать более слабое заключение).

Этот перечень ни в коем случае не является исчерпывающим. Существуют и другие типичные указания и признаки, но нам нет необходимости их здесь перечислять. Во всяком случае, было бы бесполезно перечислять их без должной иллюстрации[157].

8. Индукция в изобретении. Предположение A человека, решающего задачу (что его план решения можно осуществить), может

384

быть подкреплено одним, двумя или большим числом указаний B₁, B₂, B₃, ... (того же типа, что и перечисленные в предыдущем § 7). Такие указания могут прийти ему на ум одно за другим, каждое указание увеличивает его уверенность в своем плане. Наши предыдущие обсуждения приводят нас к сравнению такого процесса решения задачи с индуктивным процессом, в котором исследователю, рассматривающему предположение A, удается подтвердить одно за другим несколько следствий B₁, B₂, B₃, ... Мы можем также сравнить его с судебной процедурой, в течение которой присяжные, исследуя обвинение A, замечают одно за другим несколько подтверждающих улик B₁, B₂, B₃, ... Нам не следует наивно ожидать тождественности этих трех процессов, но мы должны исследовать их сходство или различие без предвзятого мнения.

(1) Когда человек, решающий задачу, обдумывает свой план решения, этот план обычно является скорее «текучим», чем «жестким», он больше чувствуется, чем формулируется. В самом деле, для этого человека было бы глупо преждевременно фиксировать свой план. Умный человек не связывает себя жестким планом. Даже на более позднем этапе, когда план более созреет, он сохраняет этот план пригодным для видоизменений, оставляет ему некоторую гибкость, принимает во внимание непредвиденные трудности, к которым он может оказаться вынужденным приспосабливать свой план. Поэтому, когда он исследует осуществимость своего плана, он рассматривает изменчивый, иногда очень недолговечный объект.

С другой стороны, предположения, которые исследует математик или натуралист, обычно являются довольно определенными: они ясно сформулированы или по крайней мере разумно близки к ясной формулировке. И присяжные должны исследовать довольно определенное предположение: обвинительный акт, выражения которого тщательно подобраны обвинением.

Отметим это существенное различие между исследованием человеком, решающим задачу, осуществимости его плана и индуктивным исследованием математического или физического предположения или судебным исследованием обвинения: это различие между изменчивым, или очень недолговечным, и неизменным, сравнительно хорошо определенным объектом.

(2) Заседания и решения суда присяжных заносятся в протокол. Предположение, исследуемое натуралистом, и доводы, собранные за или против него, также предназначены для постоянного протоколирования. Не так обстоит дело с предположением человека, решающего задачу, относительно осуществимости его схемы или с признаками, говорящими за или против нее: их значение мимолетно. Они крайне важны в то время, когда они руководят действиями человека, решающего задачу. Но когда его работа вступает в новую фазу, сам план может измениться, и тогда указания, говорящие за или против этого плана, теряют почти всякий интерес. В конце,

385

когда решение достигнуто и задача решена, все такие аксессуары отбрасываются. Окончательная форма решения может быть записана, но изменявшиеся планы и аргументы за или против них в большей части или целиком забываются. Воздвигнутое здание остается на виду, но леса, которые были необходимы, чтобы его воздвигнуть, удаляются.

Отметим этот аспект различия между индуктивным или судебным исследованием, с одной стороны, и оценкой человеком, решающим задачу, перспектив своего плана — с другой: первое постоянно протоколируется, а второе нет.

(3) Предположение A и указания B₁, B₂, B₃, ..., перечисленные в § 7, можно интерпретировать с известной широтой. После предыдущих замечаний [в (1) и (2)] нам не следует ожидать, что слишком часто будет применима четко определенная интерпретация. Все же есть некоторое преимущество в том, чтобы начать с такой интерпретации. Рассмотрим предположение A человека, решающего задачу, и указание B, подкрепляющее это предположение, в следующих формулировках:

A. Этот план решения можно осуществить в его теперешней форме.

В. Этот план решения принимает в расчет все данные.

Чтобы описать эту ситуацию точнее, прибавим: Известно, что каждое из данных необходимо. Если это так, то

Из A следует B.

Действительно, если бы план мог быть осуществлен и дать правильное решение, он должен был бы использовать все данные, каждое из которых необходимо для решения.

Теперь важно ясно себе представить ситуацию: A — предположение, в котором человек, решающий задачу, естественно заинтересован, B — утверждение, которое может быть истинным или нет. Исследуем обе возможности.

(4) Если для решения необходимы все данные, но наш план решения не принимает всех данных в расчет, то наш план в его теперешней форме не может быть осуществлен. (Он мог бы быть осуществлен в видоизмененной форме.) Иными словами, если B ложно, то и A должно быть ложно.

Теперь важно отметить, что мы могли бы прийти к этому заключению и с помощью формального рассуждения. Действительно, мы следовали здесь классической элементарной схеме рассуждения «modus tollens», так называемого гипотетического силлогизма:

Из A следует B
В ложно

A ложно

(5) Если, однако, наш план решения действительно принимает в расчет все данные, то естественно рассматривать это обстоятельство

386

как благоприятный признак, как хорошую примету, что наш план может быть осуществлен. (Я представляю себе вид человека, решающего задачу, когда он замечает, что данное, которое, как ему казалось сначала, его план не учитывает, в конце концов оказалось использованным планом, и при этом хорошо использованным.) Короче говоря, если B истинно, то A становится более правдоподобным. Теперь важно отметить, что в действительности мы могли бы прийти к этому заключению, просто следуя нашей фундаментальной индуктивной схеме:

Из A следует B

В истинно

A более правдоподобно

(6) Рассмотрим теперь другую ситуацию. Она сходна с ситуацией, объясненной в (3) и разобранной в (4) и (5), но явным образом от нее отлична. Снова мы интересуемся предположением A человека, решающего задачу, и указанием B, подкрепляющим это предположение. Однако ситуация теперь иная (менее четко определенная). A и B имеют значения:

A. Этот план решения может быть осуществлен (быть может, в видоизмененной форме).

B. Этот план решения принимает в расчет все данные.

Чтобы охарактеризовать эту ситуацию более полно, прибавим: Мы сильно подозреваем, хотя и не знаем определенно, что все данные необходимы.

Как и выше, A — предположение, в котором человек, решающий задачу, очень заинтересован, а B — утверждение, которое может быть истинным или нет. Мы должны исследовать обе возможности.

Если B оказывается ложным, то появляется довод против A, но он не является полностью решающим. Поскольку B ложно, наш план не принимает в расчет всех данных; тем не менее мы можем придерживаться нашего плана (если мы имеем для него какое-нибудь сильное, хотя и ясно не сформулированное основание). Может иметься некоторое (еще не ставшее ясным) основание надеяться, что в конечном счете какая-нибудь модификация нашего плана будет учитывать все данные. Некоторое влияние на нас могло бы оказать и сомнение в том, что все данные необходимы.

Если B оказывается истинным, то мы можем принять это обстоятельство за ободряющий признак. Действительно, даже если из A не следует B, и, таким образом, B вместе с A не является несомненным, все же может быть, что

B вместе с A весьма правдоподобно,

B без A не в такой мере правдоподобно.

В таком случае подтверждение можно рассматривать как своего рода косвенную улику в пользу A. [Ср. § 13.13 (5).]

387

(7) В предыдущих пунктах (3), (4), (5) и (6) мы рассмотрели указание, обозначенное в § 7 символом B₁ (мы обозначали его просто B). Рассмотрение других указаний, перечисленных в § 7 (указаний B₂, B₃, ..., B₆), обнаружило бы подобную же картину.

Как мы уже видели, из A может следовать B₁, но даже если это и не так и B₁ не обязательно присоединяется к A, могут иметься сильные шансы в пользу того, что A будет сопровождаться B₁. Такой же характер имеет отношение A к B₂ (или B₃, или B₄, ...). Если план человека, решающего задачу, хорош, то он должен создавать какую-то связь между данными и неизвестным (или между посылкой и заключением); ср. B₂. Не является абсолютно необходимым, чтобы решение было сходно с решением какой-либо ранее решенной сходной задачи, однако обычно довольно велики шансы того, чтобы это было так; ср. B₃, B₄. Если план осуществляется для всей. задачи, то он должен, конечно, осуществляться для любого частного случая или любой части этой задачи; ср. B₅, B₆.

Следовательно, если мы сомневаемся в предположении A, но нам удалось наблюдать B₁, или B₂, или B₂, ..., то мы можем разумно рассматривать наше наблюдение как некоторого рода индуктивные доводы или косвенные улики в пользу A, как указание в пользу предположения человека, решающего задачу, что его план можно осуществить.

(8) Если, несмотря на значительный труд, натуралисту удается подтвердить только несколько, не слишком уж неожиданных следствий своего предположения, то он может быть вынужден от него отказаться. Если против подсудимого предъявлено слишком мало улик, суд может прекратить дело. Если после долгих и напряженных усилий человеку, решающему задачу, пришло на ум только несколько слабых указаний в пользу его плана, то он может быть вынужден радикально изменить свой план или даже совсем его отбросить.

С другой стороны, если было подтверждено несколько следствий, было предъявлено несколько улик против подсудимого, было подмечено несколько указаний, то доводы в пользу предположения натуралиста, в пользу обвинения или в пользу плана человека, решающего задачу, могут значительно усилиться. Однако даже более важную роль, чем число, может играть разнообразие. Следствия, очень отличающиеся одно от другого, свидетели, являющиеся очевидно независимыми, указания, приходящие с различных сторон, следует рассматривать как более веские.

(9) Несмотря на такое сходство, существует и заметное различие. Цель натуралиста — собрать за или против своего предположения столько доводов, сколько ему удастся. Цель суда — исследовать все относящиеся к делу предъявленные улики. Однако цель человека, решающего задачу, отнюдь не состоит в том, чтобы собрать столько, сколько ему удастся, доводов за или против своего плана решения или до самого конца обдумать эти доводы: его цель — решить

388

задачу любыми средствами, следуя своему плану решения, или какому-нибудь другому плану, или не следуя никакому плану.

Даже ошибочный план может служить цели человека, решающего задачу. Чтобы решить свою задачу, он должен мобилизовать и организовать относящиеся к рассматриваемому вопросу части своего прошлого опыта. Работая с ошибочным планом, но с настоящим напряжением, он может расшевелить какую-нибудь подходящую идею, которая в противном случае осталась бы скрытой и не пробужденной[272] в его фоне[158]; это может дать ему новую отправную точку. При решении задачи плохой план часто оказывается полезным; он может вести к лучшему плану.

(10) Два человека, которым представлены одни и те же доводы, могут честно быть не согласны, даже если они руководствуются одними и теми же схемами правдоподобных рассуждений. Их фоны могут быть различными. Мои несформулированные, неясные основания, весь мой фон может оказывать влияние на мою оценку экспериментальных данных или судебных улик. Еще большее влияние могут они оказывать на мою оценку указаний за или против моего плана решения, и это не неразумно. Разумно, что, работая над решением задачи, больше веса, чем при других условиях, я должен придавать внушениям моего фона, и меньше веса — отчетливо сформулированным основаниям: расшевелить подходящий материал, скрытый где-то в фоне, — вот для чего я работаю.

Тем не менее мне кажется, что одно из главных достоинств человека, закаленного в решении задач, состоит в том, что он может проницательно оценивать указания за или против осуществимости своего плана, как прошедший хорошую школу натуралист оценивает экспериментальные данные или опытный юрист — судебные улики.

9. Несколько слов преподавателю. Математику можно рассматривать с различных точек зрения. Многим учащимся, я опасаюсь, математика кажется собранием жестких правил, часть из которых перед заключительными экзаменами следует выучить наизусть, и все их после этого можно позабыть. Некоторым преподавателям математика кажется системой строгих доказательств, от изложения которых в классе следует, однако, воздержаться, а вместо них изложить какой-нибудь более доступный, хотя и не имеющий силы доказательства рассказ, которого вы немножко стыдитесь. Математику, являющемуся активным исследователем, математика иногда может казаться игрой в догадки: вы должны догадаться о математической теореме, перед тем как ее докажете, вы должны догадаться об идее доказательства, перед тем как проведете его в деталях.

Философу с довольно широкими взглядами, я думаю, все разумные приобретения знаний должны иногда казаться игрой в догадки. В науке, как и в повседневной жизни, встретившись с новой ситуацией, мы начинаем с какой-нибудь догадки. Наша первая догадка может бить мимо цели, но мы испытываем ее и в соответствии со степенью успеха более или менее ее видоизменяем. В конечном счете после нескольких испытаний и нескольких видоизменений, толкаемые наблюдениями и ведомые аналогией, мы можем прийти к более удовлетворительной догадке. Неспециалист не находит удивительным, что натуралист работает таким образом. Знания натуралиста могут быть лучше упорядочены с целью отбора подходящих аналогий, его наблюдения могут быть более целеустремленны и более тщательны, он может давать своим догадкам более причудливые названия и называть их «ориентировочными обобщениями», но натуралист подобно обычному человеку приспосабливает свой ум к новой ситуации с помощью догадок. И неспециалист не удивляется, когда слышит, что натуралист подобно ему самому догадывается. Неспециалисту может казаться несколько более удивительным, что и математик также догадывается. Результат творческой работы математика — доказательное рассуждение, доказательство, но доказательство открывают с помощью правдоподобных рассуждений, с помощью догадки.

Если это так, а я верю, что это так, то для догадки должно быть место и в преподавании математики. Обучение должно подготавливать к изобретению, или по крайней мере давать некоторое представление об изобретении. Во всяком случае, обучение не должно подавлять в учащемся ростки изобретательности. Учащийся, немного интересующийся рассматриваемой в классе задачей, ожидает решение определенного типа. Если учащийся смышлен, то он в какой-то мере предвидит решение: результат может выглядеть так-то и так-то, и есть шансы, что он может быть получен с помощью такого-то и такого-то приема. Преподаватель должен пытаться ясно понять, что могли бы ожидать учащиеся, он должен узнать, что они на самом деле ожидают, должен указать, что они должны были бы разумно ожидать. Если учащийся менее смышлен и особенно если ему надоело, то он, вероятно, будет высказывать дикие и безответственные догадки. Преподаватель должен показать, что догадки в области математики могут быть разумными, серьезными, ответственными. Я обращаюсь к преподавателям математики всех степеней и говорю: Давайте учить догадываться!

Я не говорю, что мы должны пренебрегать доказательствами. Наоборот, нам следует учить и доказывать и догадываться, учить обоим видам рассуждений: доказательному и правдоподобному. Для учащегося ценнее, чем любому частному математическому факту или приему, теореме или аппарату, научиться двум следующим вещам:

Во-первых, отличать строгое доказательство от нестрогой попытки, доказательство от догадки.

Во-вторых, отличать более разумную догадку от менее разумной догадки.

390

Существуют частные случаи, когда важнее учить догадываться, чем доказывать. Возьмите преподавание дифференциального и интегрального исчисления студентам технических учебных заведений. (Я имею длительный и разнообразный опыт такого преподавания.) Инженерам нужна математика, совсем немногие из них имеют здоровый интерес к математике, но они не приучаются понимать ε-доказательства, не имеют времени для ε-доказательств, не интересуются ε-доказательствами. Преподавать им правила дифференциального и интегрального исчисления как догму, ниспосланную свыше, было бы непедагогично. Делать вид, что ваше доказательство является полным, когда на самом деле это не так, было бы нечестно. Спокойно признайте, что ваши доказательства являются неполными, но дайте достойные правдоподобные основания для неполно доказанных результатов, пользуясь примерами и аналогией. Тогда вам не нужно будет стыдиться поддельных доказательств, и некоторые студенты смогут помнить то, чему вы их учили, и после экзаменов. На основании долгого опыта я сказал бы, что одаренным студентам технических учебных заведений обычно более доступны хорошо изложенные правдоподобные доводы, чем строгие доказательства, и студенты более благодарны таким доводам.

Я сказал, что желательно учить догадываться, но не сказал, что этому учить легко. Нет никакого абсолютно верного метода для догадок, и потому не может быть никакого абсолютно верного метода для обучения тому, как догадываться. Я мог, пожалуй, в предыдущем сказать несколько глупостей, но, надеюсь, я избежал наибольшей глупости — претензии на то, что у меня есть безошибочный метод, позволяющий учить догадываться.

Тем не менее учить догадываться не невозможно. Я надеюсь, что в этом отношении могут оказаться полезными некоторые из подробно объясненных примеров и некоторые из предложенных в этой книге упражнений. Они имеют наилучшие шансы попасть на плодородную почву у преподавателей, имеющих длительный опыт в решении задач.

Возьмите, скажем, пример, рассмотренный в §§ 4 и 6. Два изложения в §§ 4 и 6 очень различны. Наиболее бросающееся в глаза различие состоит в том, что одно из них короткое, а другое длинное. Наиболее существенное различие состоит в том, что одно дает доказательства, а другое — правдоподобности. Одно предназначено для того, чтобы проверить доказательные заключения, оправдывающие последовательные шаги. Другое приспособлено для того, чтобы дать известную возможность заглянуть в эвристические мотивы некоторых шагов. Доказательное изложение следует принятому способу, обычному со времен Евклида; эвристическое изложение крайне необычно в печати. Однако наблюдательный преподаватель может пользоваться обоими способами изложения. Действительно, он мог бы придумать, если нужно, третье изложение, находящееся между

391

этими двумя, с должным учетом имеющегося в распоряжении времени интереса своих учеников, всех условий, в которых он работает[159].

Эта книга главным образом адресуется учащимся, желающим развить свои способности, и читателям, желающим узнать о правдоподобных рассуждениях и их не столь уж банальных связях с математикой. Не игнорировались, я надеюсь, и интересы преподавателя, но они удовлетворялись скорее косвенно, чем прямо. Я надеюсь когда-нибудь восполнить этот пробел. Тем временем я повторяю свою надежду, что эта книга, как она есть, может быть полезной некоторым преподавателям, по крайней мере тем преподавателям, которые имеют настоящий опыт в решении задач. Трудность состоит в том, что существует так мало преподавателей математики, имеющих этот опыт. И даже наилучший педагогический институт до сих пор не добился успеха в выпуске изумительного преподавателя, имеющего настолько превосходную выучку в методах преподавания, что он может заставить своих учеников понять даже то, чего не понимает сам.

ПРИМЕРЫ И ПРИМЕЧАНИЯ К ГЛАВЕ XVI

1. Преподавателю: некоторые типы задач. Эта книга предназначена служить различным категориям читателей: тем, кто желает понять, как догадываются, тем, кто желает научиться догадываться, и тем, кто желает учить догадываться. Читатель последней категории редко является непосредственным адресатом, но наблюдательный преподаватель мог бы кое-чему научиться и на изложенных в этой книге примерах и на способе изложения. Он мог бы, например, увидеть, что имеются способы постановки задач, очень отличающиеся от обычного способа. Я хочу указать несколько типов задач — задачи «догадаться и доказать», задачи «испытать следствия», задачи «вы можете сделать ошибочную догадку» и задачи «теория в малом масштабе». Все эти типы задач могут быть использованы наблюдательным преподавателем, чтобы привлечь интерес своих более смышленых учеников и освободить их от однообразных и стандартных задач, наполняющих учебники.

Догадаться и доказать. О математических фактах сначала догадываются, а затем их доказывают, и почти каждое место в этой книге старается показать, что это — нормальный образ действий. Если изучение математики должно иметь какое-нибудь отношение к математическим открытиям, то учащемуся должна быть дана какая-то возможность делать те задачи, в которых он сначала догадывается о некотором математическом факте, а затем доказывает его на подходящем уровне. Тем не менее обычные учебники этой возможности не предоставляют: примеры 1.2, 5.1, 5.2, 7.1—7.6 (и многие другие) предоставляют такую возможность.

Испытать следствия. Философы и нефилософы расходятся в мнениях относительно почти всего, касающегося индукции, но существует мало сомнений в том, что наиболее обычный индуктивный прием состоит в исследовании общего утверждения путем испытания его частных следствий. Этот индуктивный прием ежедневно применяется в математическом исследовании и мог бы ежедневно применяться в классе с реальной пользой для учащихся. См. пример 12.2 и примеры 12.3–12.6. Ср. пример 6.

Вы можете сделать ошибочную догадку. Вам следовало бы приобрести некоторый опыт в догадках. Вам следовало бы из личного соприкосновения

392

с реальными вещами знать, что догадки могут быть серьезными, что догадки могут вести к ошибке и что даже ваши собственные вполне серьезные догадки могут вести к ошибке. Для такого опыта решите примеры 11.1–11.12.

Теория в малом масштабе. Почти на каждой странице этой книги какая-нибудь относительно элементарная задача обсуждается таким образом, чтобы обсуждение проливало некоторый свет на вопросы, которые могут возникнуть в связи с другими, не столь элементарными задачами. Есть основание предпочитать такое «исследование в малом масштабе»: менее элементарная задача может показать рассматриваемый вопрос в масштабе, производящем более сильное впечатление, но она требовала бы значительно более длинных объяснений и значительно больших предварительных знаний. Не слишком легко «уменьшить масштаб»: элементарные задачи, достаточно ярко показывающие существенные свойства правдоподобных рассуждений или рассуждений, связанных с изобретением, может оказаться трудным найти. Возможно также, но это еще труднее, придумать элементарные задачи, чтобы проиллюстрировать действия ученого при построении теории. Нижеследующие примеры 2, 3 и 4 предлагают такие задачи «теории в малом масштабе», примеры 5 и 6 несколько сходны с ними.

2. Четырехугольник разрезается своими двумя диагоналями на четыре треугольника. Назовем два из этих треугольников «противоположными», если они имеют общую вершину, но не имеют общей стороны. Докажите утверждения:

(a) Произведение площадей двух противоположных треугольников равно произведению площадей двух других противоположных треугольников.

(b) Четырехугольник является трапецией в том и только в том случае, если существуют два равновеликих противоположных треугольника.

(c) Четырехугольник является параллелограммом в том и только в том случае, если все четыре треугольника равновелики.

3. (a) Докажите следующую теорему: Точка лежит внутри равностороннего треугольника и имеет соответственно расстояния x, y и z от трех его сторон; h — высота треугольника. Тогда x + y + z = h.

(b) Точно сформулируйте и докажите аналогичную теорему пространственной геометрии относительно расстояний внутренней точки от четырех граней правильного тетраэдра.

(c) Обобщите обе теоремы так, чтобы они относились к любой точке соответственно на плоскости или в пространстве (а не только к точкам внутри треугольника или тетраэдра). Дайте точные формулировки и доказательства.

4. Рассмотрите предложения (I)–(IV), которые не обязательно верны:

(I) Если многоугольник, вписанный в окружность, является равносторонним, то он также и равноугольный.

(II) Если многоугольник, вписанный в окружность, является равноугольным, то он также и равносторонний.

(III) Если многоугольник, описанный вокруг окружности, является равносторонним, то он также и равноугольный.

(IV) Если многоугольник, описанный вокруг окружности, является равноугольным, то он также и равносторонний.

(a) Установите, какие из этих четырех предложений верны и какие неверны, давая в каждом случае доказательство вашего утверждения.

(b) Если вместо произвольных многоугольников мы рассматривали бы только четырехугольники, то какие из этих четырех предложений были бы верны и какие неверны?

(c) Как обстоит дело с пятиугольниками?

(d) Можете вы догадаться о каких-нибудь более широких утверждениях или, быть может, даже доказать их? Они должны объяснить ваши наблюдения (b) и (c).

5. Пусть α, β и γ — углы треугольника. Покажите, что

(b) sin 2α + sin 2β + sin 2γ = 4sin α·sin β·sin γ,

(c) sin 4α + sin 4β + sin 4γ = –4sin 2α·sin 2β·sin 2γ.

393

6. Рассмотрите усеченную правильную пирамиду с квадратными основаниями. Назовите «средним сечением» сечение усеченной пирамиды плоскостью, параллельной основаниям и находящейся от них на одинаковом расстоянии. Назовите «промежуточным прямоугольником» прямоугольник, одна сторона которого равна стороне нижнего, а другая — стороне верхнего основания.

Четыре различных ваших друга согласны, что объем этой усеченной пирамиды равен произведению высоты на некоторую площадь, но они расходятся в мнениях относительно этой площади и делают четыре различных предположения:

(I) Площадь среднего сечения.

(II) Среднее арифметическое площадей нижнего и верхнего оснований.

(III) Среднее арифметическое площадей нижнего и верхнего оснований и среднего сечения.

(IV) Среднее арифметическое площадей нижнего и верхнего оснований и промежуточного прямоугольника.

Пусть h — высота усеченной пирамиды, a — сторона ее нижнего основания и b — сторона ее верхнего основания. Выразите каждое из четырех предложенных правил в математических обозначениях, решите верно оно или нет и докажите ваш ответ.

7. Qui nimium probat, nihil probat. Иными словами, если вы доказываете слишком много, то вы ничего не доказываете. Я не могу сказать, в каком смысле изобретатель этой классической поговорки намеревался ею пользоваться, но хочу объяснить то значение этого изречения, которое с тех пор, как я приступил к математической работе, я нахожу чрезвычайно полезным. Это изречение напоминает мне об одном из наиболее полезных признаков, с помощью которых мы можем судить об осуществимости плана решения.

Вот ситуация: вы хотите доказать какое-то предложение. Это предложение состоит из заключения и посылки, которая имеет несколько пунктов, и вы знаете, что каждый из этих пунктов необходим для заключения, т.е. что ни один из них не может быть отброшен без того, чтобы заключение вашего предложения не стало несправедливым. Вы задумали план доказательства и взвешиваете шансы вашего плана. Если ваш план не вовлекает в игру все эти пункты, то вам следует видоизменить ваш план или же отвергнуть его: если бы он был осуществим, как он есть, и привел бы к доказательству заключения, хотя он и не учитывает тот или иной пункт посылки, то он доказал бы слишком много, т.е. нечто ложное, и таким образом он не доказал бы ничего.

Я сказал, что ваш план должен вовлекать в игру эти пункты. Я имею в виду, что одних лишь словоизлияний не достаточно, простое их упоминание в счет не идет: ваш план должен обеспечивать существенное использование каждого пункта посылки в доказательстве. Каркас, который должен поддерживать заключение, не может быть воздвигнут, если он не имеет крепкой опоры в каждом пункте посылки.

Может оказаться очень трудным придумать план, должным образом вовлекающий в игру все пункты посылки. Поэтому, если план обещает уловить все эти пункты, то мы приветствуем его с облегчением: это превосходный признак, сильное указание на то, что план можно осуществить.

По поводу соответствующих «задач на нахождение», все данные которых необходимы, см. § 8 (3), (4), (5).

Если вы предпочитаете латинской поговорке французское изречение, то вот оно: «La mariée est trop belle» — новобрачная слишком красива. Я не думаю, что мне нужно распространяться на эту тему; после предыдущего читатель может сам представить себе все подробности.

8. Близость и правдоподобность. Насколько далеко решение? Сколько остается доделать? Такие вопросы тяжелым грузом лежат на сознании учащегося, который должен окончить свою задачу за назначенное время, но они присутствуют в сознании каждого человека, решающего задачу.

(1) Мы даже в состоянии до некоторой степени ответить на такие вопросы, конечно, не точно, но я склонен верить, что в среднем довольно правильно.

394

Например, посмотрим снова на рис. 16.1—16.5 и на процесс решения, который они изображают. Человек, решающий задачу, может чувствовать, что рис. 16.3 значительно ближе к решению, чем рис. 16.2; и как только он придет к рис. 16.4, он может чувствовать, что решение в пределах легкой достижимости.

Оценивая близость решения, мы можем полагаться на неясные чувства или на более отчетливые признаки. Любой признак, указывающий, что наш план решения осуществим, может быть истолкован также и как признак продвижения к решению и может помочь нам оценить расстояние, которое нам еще осталось пройти.

(2) Рассмотрим решение «задачи на доказательство». Цель состоит в доказательстве (или опровержении) некоторой теоремы. Человек, решающий задачу, может верить или не верить в теорему, которую он доказывает. Однако, если он сколько-нибудь хорошо умеет решать задачи, то он должен быть готов к пересмотру своих мнений. И, таким образом, вопросы «Правдоподобна ли теорема? Насколько она правдоподобна?» всегда присутствуют в его сознании, хотя иногда более, а иногда менее на переднем плане. Если в его поле зрения попадает что-либо новое, то у него есть два вопроса: «Это делает теорему более правдоподобной или менее правдоподобной? Приближает ли это решение или нет?» Его внимание, конечно, может быть настолько поглощено новым фактом, что он не находит времени для формулировки этих вопросов в словах. Он может и ответ себе дать без слов. Даже если он говорит «Хороший признак» или «Плохой признак», то он едва ли даст себе труд подробно выразить, что он имеет в виду. Есть это признак близости решения или признак правдоподобности теоремы? Однако, если он хорошо умеет решать задачи, то он достаточно хорошо знает важное различие между близостью и правдоподобностью, и это различие проявится в его работе, в его подходе к задаче.

(3) Припоминание когда-то известной, но теперь забытой фамилии является задачей более простой, чем математическая задача, но несколько с ней сходной. Мы часто можем наблюдать людей, пытающихся припомнить фамилию, и на таких наблюдениях мы могли бы научиться нескольким интересным вещам.

В разговоре ваш друг хочет назвать вам какую-то фамилию (хозяина магазина, или фамилию знакомого, или, может быть, автора). Он запинается, и вы слышите его слова: «Сейчас я ее назову», или «Подождите немножко, я через некоторое время ее вспомню», или «Как это ни глупо, но я не могу теперь вспомнить, хотя уверен, что эта фамилия придет мне в голову через несколько часов, возможно, завтра утром». Очевидно, ваш друг пытается оценить близость этой фамилии, пытается измерить своего рода «психологическое расстояние». Я высказал бы догадку, что его предсказание окажется приблизительно верным, что его оценка этого «психологического расстояния» в общих чертах правильна.

С точки зрения возможного сравнения с решением задачи интересно также отметить, что человек, который не в состоянии вспомнить фамилию полностью, может быть в состоянии вспомнить ее частично или, пожалуй, лучше сказать, он может быть в состоянии вспомнить некоторые черты этой фамилии. Вы можете слышать, как ваш друг говорит: «Фамилия не Баттенберг — он, в конце концов, не муж королевы[160],⁵ — но это немецкая фамилия из трех слогов, очень похожая на Баттенберг». И (я наблюдал такие случаи) ваш друг, может быть, совершенно прав во всех этих подробностях, хотя правильная фамилия придет ему на ум только через несколько дней.

Совсем таким же образом математик, хотя он еще и не решил свою задачу, может предвидеть некоторые черты ее решения вполне надежно.

Те аспекты решения задач, которые наиболее интересны для будущего математика или для преподавателя, не легко поддаются обычным методам экспе-

395

риментальной психологии. Возможно, припоминание фамилии, процесс в каких-то отношениях сходный с решением математической задачи, может быть легче введено в рамки психологических экспериментов.

9. Вычисления и правдоподобные рассуждения. Хотя числа часто рассматриваются как символы наиболее высокой достижимой достоверности, результаты вычислений никоим образом не являются достоверными; они только правдоподобны. Вычисления во многих отношениях зависят от правдоподобных рассуждений.

(1) Вы должны проделать длинное вычисление. Окончательный результат достигается последовательностью шагов. У вас очень хорошие шансы сделать правильно любой отдельный шаг, но шагов много, в каждом шаге есть возможность ошибиться, и окончательный результат может быть неверным. Как предохранить себя от ошибки?

Вычислите искомое число дважды с помощью как можно более отличающихся способов. Если эти два вычисления дадут различные результаты, то, несомненно, по крайней мере один из них неверен, но, возможно, что и оба неверны. Если два вычисления находятся в согласии, то никоим образом не несомненно, что дважды полученный результат правилен, но он может оказаться правильным, а согласие является указанием его правильности. Вес этого указания зависит от различия между двумя способами, которыми мы воспользовались.

Например, этот вес очень мал, если, проделав вычисление один раз, вы немедленно после этого повторите его без какого бы то ни было изменения в методе: с первым вычислением, еще свежим в вашем уме и в ваших пальцах, вы легко можете оступиться на том же месте, где оступились в первый раз. Повторить вычисление после того, как пройдет известное время, немножко лучше, дать проделать его во второй раз другому человеку значительно лучше, проделать второе вычисление совсем другим методом еще лучше.

Действительно, если два совершенно различных способа приводят к одинаковому результату, то мы имеем только два очевидных предположения: результат может быть правильным или согласие может быть вызвано случайностью. Если вероятность согласия из-за простой случайности очень мала, то второе из двух соперничающих предположений соответственно неправдоподобно, мы склонны его отвергнуть, и, таким образом, мы расположены с большим доверием относиться к первому предположению, т.е. мы можем больше полагаться на правильность результата.

Чем больше отличаются способы двух вычислений, тем более реалистична простейшая оценка вероятности их согласия: вероятность того, что два вычисления из-за простой случайности приведут к одним и тем же n цифрам, равна 10^–n; ср. § 14.9 (3), пример 14.11, но также и пример 14.32 и пример 12.

При вычислениях большого масштаба является хорошим обычаем делать случайность совпадения еще более невероятной посредством введения многократного контроля. Два вычисления выполняются методами, настолько различными, насколько возможно по обстоятельствам, однако так, чтобы, если они правильны, совпадали не только их окончательные результаты, но и несколько промежуточных результатов. Когда степень согласия возрастает, становится все более и более трудно приписать его простой случайности, хотя, конечно, случайность никогда не может быть полностью исключена и результат никогда не может быть полностью гарантирован.

(2) До сих пор мы молчаливо допускали как известное, что два вычисления, результаты которых мы сравниваем, теоретически строго эквивалентны. Однако в прикладной математике мы часто должны работать с приближениями и можем сравнивать числовые результаты, которые не обязаны полностью совпадать, даже если все совершаемые арифметические операции безошибочны; мы только надеемся, что они будут «грубо» совпадать. Кроме того, теория метода приближения, с которым мы работаем, может быть очень плохо известна. При таких обстоятельствах, конечно, сфера приложения правдоподобных рассуждений является даже более широкой и такие рассуждения более рискованны. Ср. пример 11.23.

396

(3) Два математика, A к B, исследовали одно и то же множество из девяти комбинаторных задач. Нам нет необходимости знать содержание этих задач (они относятся к гиперкубу в четырехмерном пространстве), но важно знать, что они расположены в порядке возрастающей трудности. Первые две задачи тривиальны, третья легкая, четвертая труднее, затем они становятся все более и более сложными, а последняя задача является наиболее трудной.

И A, и B решили задачи, но их результаты не вполне согласны. Вот их решения этих девяти задач:

A:  1  1  4  6  19  27  47  55  78;

B:  1  1  4  6  19  27  50  56  74.

Иными словами, A и B согласны в отношении первых шести задач, более легких, но несогласны в отношении трех последних задач, более трудных. На самом деле, они следовали различным методам.

A решал каждую из этих девяти задач независимо от других. Его метод для каждой задачи несколько иной, и по мере того, как он переходит к более трудным задачам, его метод становится все более сложным.

B решал задачи с помощью единого метода. Его работа состояла из двух частей. Первая часть, более трудная, была подготовительной для решения всех девяти задач. Вторая часть, более стандартная, применяла результат первой части к каждой отдельной задаче в соответствии с единообразным правилом. При решении задач методом математика B они кажутся значительно менее отличающимися по трудности, чем при их решении методом математика A.

Мне кажется, что описанная ситуация дает нам разумное основание больше верить решению B, чем решению A.

Поскольку эти два очень различных метода приводят к одинаковым результатам в первых шести задачах и эти задачи как-никак более легкие, то существует достаточное основание верить, что решение этих задач правильно. В отношении первых трех задач нет никаких сомнений.

Так как результат первой части работы математика B в 3 случаях из 9 подтверждается своими следствиями и, по-видимому, подтверждается еще в трех случаях (он не подтверждается и не опровергается в 3 остающихся случаях), то имеется серьезное основание доверять этому результату.

Если, однако, первая часть работы B была правильна (как это, по-видимому, и есть), то он мог бы ошибиться только во второй, более стандартной части, решая последние три задачи. Но A имел наибольшие трудности в их решении. И таким образом, по-видимому, A имеет больше шансов ошибиться, чем B[161].⁶

Только что рассмотренный случай является довольно специальным, но он показывает, что существуют дальнейшие возможности в исследовании схем правдоподобных рассуждений. Например, благодарной может оказаться задача выразить, как можно лучше, только что изложенное правдоподобное рассуждение в формулах исчисления вероятностей.

10. Вы должны сложить столбец из десяти шестизначных чисел, начинающийся, например, так:

159 603

164 607

178 110

. . . . . . .

Опишите различные способы, которыми можно это сделать.

11. Назовите «элементарным шагом» прибавление написанного однозначного числа к двузначному числу, которое вы держите в уме; включите, однако, возможность (делающую шаг более легким), что второе число также написано или

397

что оно имеет только один знак. Сколько потребуется элементарных шагов, чтобы выполнить упомянутое в примере 10 сложение наиболее обычным способом?

12. Производя вычисление, вы получаете сначала два девятизначных числа, а затем окончательный результат как их разность, которая оказывается трехзначным числом. При другом способе вычисления то же самое трехзначное число вы получаете в результате как разность двух семизначных чисел. Пользуясь формулой, приведенной в примере 9 (1),вычислите вероятность того, что такое согласие вызвано случайностью.

13. Формальное доказательство и правдоподобные рассуждения. Вы должны проделать длинное вычисление. Окончательный результат достигается последовательностью шагов и должен быть правильным, если правилен каждый шаг. Каждый отдельный шаг (например, сложение 3 + 7 или умножение 3 × 7) так прост и знаком, что при сколько-нибудь благоприятных обстоятельствах, когда ваше внимание «не отвлечено», вы не можете ошибиться. Тем не менее, подобно всякому другому, вы можете делать ошибки в вычислении. После того как вы весьма тщательно выполните эти последовательные шаги, вам не следовало бы без проверки доверять окончательному результату.

Вы проводите длинное математическое доказательство. Предполагается, что это доказательство разлагается на шаги, каждый из которых вы полностью можете проверить, и окончательное заключение должно быть правильным, если правилен каждый шаг. Однако подобно всякому другому, вы можете делать ошибки. Весьма тщательно проверив эти последовательные шаги, можете ли вы доверять окончательному заключению? Не более, а возможно и менее, чем окончательному результату длинного вычисления.

Действительно, математик, проверивший детали доказательства шаг за шагом и нашедший каждый шаг в порядке, все же может быть не убежден. Для убежденности ему нужно нечто большее, чем правильность каждой детали. Что же?

Он хочет понять доказательство. После того как он пробился через доказательство, шаг за шагом, он берет на себя больший труд: он пересматривает, перерабатывает, переформулирует и перерасполагает эти шаги до тех пор, пока ему не удается сгруппировать детали в доступное пониманию целое. Только тогда он начинает доверять доказательству.

Я не отважился бы анализировать, что составляет «понимание». Некоторые говорят, что оно основано на «интуиции», и ощущение целого и группировку деталей в хорошо упорядоченное гармоничное целое они приписывают интуиции. Я не отважился бы этому противоречить, хотя у меня есть некоторые опасения[162].⁷ Однако я хочу привлечь внимание к одному обстоятельству, на мысль о котором настойчиво наводят примеры и обсуждения в этой книге.

Некоторая практика может убедить нас, что аналогия и частные случаи могут быть полезны и в отыскании, и в понимании математических доказательств. С помощью аналогии могут быть подсказаны или сделаны более ясными общий план или значительные части доказательства. Доказательство могут подсказывать и частные случаи (см., например, § 3.17); с другой стороны, мы можем проверить уже сформулированное доказательство, наблюдая, как оно проходит в знакомых или критических частных случаях. Однако аналогия и частные случаи являются наиболее обильными источниками правдоподобных рассуждений: возможно, они не только помогают создавать доказательное рассуждение и делать его более понятным, но и увеличивают наше доверие к нему. И это заставляет нас подозревать, что значительная часть нашей уверенности в доказательных рассуждениях может проистекать из правдоподобных рассуждений.

РЕШЕНИЯ

Среди предложенных для решения примеров есть примеры, взятые из двух сборников: William Lowell Putnam Mathematical Competition, Stanford University Competition Examination in Mathematics. Этот факт указывается в начале решения вместе с годом, когда была предложена задача, как «Путнэм 1948» или «Стэнфорд 1946». Задачи из «Putnam Examination» ежегодно публикуются в журнале «American Mathematical Monthly» и большая часть «Stanford Examination» также была опубликована там же.

ГЛАВА I

1. Простые числа, оканчивающиеся на 1.

2. [Стэнфорд 1948]

(n² + 1) + (n² + 2) + … + (n + 1)² = n³ + (n + 1)³.

Члены в левой части равенства образуют арифметическую прогрессию.

3. 1+ 3+ … + (2n — 1) = n².

4. 1, 9, 36, 100, … — квадраты.

5. [Стэнфорд 1949]

в зависимости от того, является ли n нечетным или четным. Единый закон для двух случаев: целое число, ближайшее к (n + 1)²/4.

6. Первый вопрос: Да. Второй вопрос: Нет, 33 — не простое число.

7. Не для вас, если у вас есть некоторый опыт в отношении простых чисел [примеры 1, 6, 9]. В действительности (1) можно доказать [как частный случай одной теоремы Kaluza, Mathematische Zeitschrift, 28 (1928), 160—170], а (2) опровергнуть: следующий коэффициент при x⁷) равен –3447 = –3·3·383. слова «формальные вычисления» имеют ясный смысл: полагая

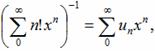
определяем u = 1 и u₁, u₂, u₃, … последовательно из равенств

0! u_n + 1! u_n—1 + 2! u_n—2, + … + (n—1)! u₁ + n! u₀ = 0

для n = 1, 2, 3, …

8. На основании полученных из наблюдения данных вполне разумно подозревать, что A_n положительно и возрастает вместе с n. Однако это предположение полностью ошибочно. С помощью более сложного аппарата (интегральное исчисление, теория аналитических функций комплексного переменного) мы можем доказать, что для большого n значение A_n приближенно равно (–1)^n—1 (n—1)! (1n n)^–2.

10. В случае 2n = 60 мы должны сделать 9 или 7 испытаний (p = 3, 5, 7, 11, 13, 17, 19, 23, 29 или p' = 31, 37, 41, 43, 47, 53, 59) в зависимости от того, следуем ли мы первому или второму приему. Скорее всего, для бо́льших значений n различие между числом испытаний будет еще значительней в пользу второго приема.

Нет решения: 9, 11, 12, 13, 14.

399

ГЛАВА II

1. Я думаю, что C или D являются «правильными обобщениями, B «бьет мимо цели». B слишком общо, чтобы дать какой-либо совет, полезный в нашем конкретном случае. Вы можете предпочесть C или D; выбор зависит от вашего фона[163]). Но и C и D наталкивают на мысль начать с линейных уравнений и в конечном счете ведут к следующему плану: из первых двух (линейных!) уравнений выразить два неизвестных через третье и, подставив эти выражения в последнее уравнение, получить для третьего неизвестного квадратное уравнение. (Можете ли вы выразить из первых двух уравнений в A любые два неизвестных?) Есть два решения:

(x, y z) = (1, –2, 2), (29/13, – 2/13, 2).

2. Если повернуть пирамиду на 180° вокруг ее оси, то она совпадет сама с собой. Правильным обобщением этой пирамиды является тело, имеющее ось симметрии этого вида, а простейшее решение есть плоскость, проходящая через эту ось и данную точку (Существует бесконечное множество других решений; в силу непрерывности мы можем провести такую секущую плоскость через любую прямую, содержащую данную точку.) Заметьте, что правильная пирамида с пятиугольным основанием не допускает сравнимого по простоте решения. Сравните «Как решать задачу», стр. 114—115.

3. A является частным случаем B, если в B мы допускаем, что P может совпадать с O; однако эти две задачи равносильны: плоскости, которые требуется провести в A и B, параллельны между собой и, таким образом, из решения любой из этих задач вытекает решение другой.

Более общая задача B более доступна, если P ≠ O; выберите на двух других прямых точки Q и R так, чтобы OP = OQ = OR. Плоскость, проходящая через P, Q и R, удовлетворяет условиям задачи. Поэтому, если предложена задача A, то выгодно перейти к более общей задаче B.

4. A есть частный случай B (при p = 1), однако эти две задачи равносильны: подстановка x = yp^½ сводит B к A.

Более общая задача B более доступна: дважды продифференцируйте простой интеграл

по параметру p. Поэтому если предложена задача A, то выгодно перейти к более общей задаче B.

Заметьте, что в примере 3 мы встретились с параллельной ситуацией.

6. Крайний частный случай, когда одна из окружностей вырождается в точку, более доступен, и мы сможем к нему общий случай. Действительно, общая внешняя касательная двух окружностей остается параллельной себе, когда оба радиуса уменьшаются на одну и ту же величину, а общая внутренняя касательная остается параллельной себе, когда один из радиусов увеличивается, а другой уменьшается на ту же величину. В обоих случаях мы можем стянуть одну из окружностей в точку, не изменяя направления общей касательной.

8. «Ведущим является частный случай, когда одна из сторон угла с вершиной на окружности проходит через центр круга. Из двух таких углов путем сложения или вычитания мы можем составить произвольный угол с вершиной на окружности (Это основная идея классического доказательства; Евклид III, 20). Поразительный пример «ведущего» частного случая см. в «Как решать задачу», стр. 189—195.

12. Если две прямые на плоскости пересекаются тремя параллельными прямыми, то соответствующие отрезки пропорциональны. Это помогает доказать

400

более трудную аналогичную теорему пространственной геометрии; см. Евклид XI, 17.

13. Диагонали параллелограмма пересекаются в их общей середине.

14. Сумма двух сторон треугольника больше третьей стороны. Более простая из этих вдух аналогичных теорем (Евклид I, 20) используется в доказательстве более трудной (Евклид XI, 20).

15. Параллелепипед, прямоугольный параллелепипед (ящик), куб, биссектор двугранного угла (т. е. плоскость, делящая этот угол пополам). Биссекторы шести двугранных углов тетраэдра пересекаются в одной точке, являющейся центром шара, вписанного в тетраэдр[273].

16. Призма, прямая призма, шар. Объем шара равен объему пирамиды, основание которой имеет ту же площадь, что и поверхность шара, и высота которой равна радиусу.

17. Назовем пирамиду равнобедренной пирамидой, если все ребра, выходящие из ее вершины, равны. Все боковые грани равнобедренной пирамиды являются равнобедренными треугольниками. Основание равнобедренной пирамиды, вписано в круг, а высота равнобедренной пирамиды проходит через центр этого круга. Ср. пример 9.26.

22. Да. Замена x на –x не изменяет x², а поэтому и произведения[274], которое в соответствии с Э представляет (sin x)/x.

23. Предсказание: из Э следует

и, таким образом, по определению производной, при x→π

Подтверждение:

24. 1/6. Как пример 23 или как частный случай k = 2 примера 25.

25. Предсказание: если k — положительное число, то

Подтверждение: для N ≥ k + 1

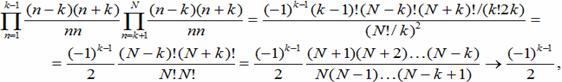
когда N стремится к ∞.

26. π/4, площадь круга диаметра 1. Из Э при x = π/2 получаем

401

Эта формула, принадлежащая Валлису (1616—1703), была хорошо известна Эйлеру. Есть другой способ записи формулы Валлиса:

27. x = πz в примере 21 и определение бесконечного произведения.

28. Да. Из примера 27 получаем

29. Из примера 27 и примера 26 получаем

30. Да. Из Э и примера 29 получаем

31. Предсказание: при x = π пример 29 дает cos π множителей

32. Предсказание: пример 29 дает cos 2π = 1.

Подтверждение: как пример 31 или как пример 31 и пример 35.

33. Предсказание: при x = nπ (n = 1, 2, 3, …) пример 29 дает

Подтверждение: из cos 0 = 1 и примера 35 или непосредственно как пример 31.

34. Да. Как пример 22.

35. Да. С помощью результата или метода примера 28.

402

36.

мы полагаем x = πz. В силу примера 27

37. Логарифмируя и дифференцируя в примере 21 или примере 27. вот точный смысл правой части:

38. В силу примера 37

Положим

для n = 1, 2, 3, … Для того чтобы найти коэффициенты a₁, a₂, a₃, …, пользуемся дифференциальным уравнением

y' + y² = –1.

Подставляя вместо y и y' их разложения и сравнивая коэффициенты при

403

одинаковых степенях x, получаем соотношения между коэффициентами a₁, a₂, a₃, …, которые наиболее удобно мы можем обозреть в таблице

		x^-2	1	x^2	x^4	x^6	…
y'		–1	a1	3a2	5a3	7a3	…
y^2	{	1	2a1	2a2	2a3	2a4	…
				a^21	2a1a2	2a1a3	…
						a^22	…
							…
		0	–1	0	0	0	…

Ср. пример 5.1. Мы получаем, таким образом, соотношения

3a₁ = –1, 5a₂ + a²₁ = 0, 7a₃ + 2a₁a₂ = 0, …

и отсюда последовательно

при n = 1, 2, 3, 4, …

39. Метод примеров 37 и 38 применяется к результату примера 36. мы полагаем теперь

Тогда

Теперь y удовлетворяет дифференциальному уравнению

2y' = 1 + y²,

которое (если заметить, что b₁ = 1) дает таблицу

		1	x	x^2	x^3	x^4	…
		1					…
y^2	{	1	2b2	2b3	2b4	2b5	…
					2b2b3	2b2b4	…
							…
							…
2y'		2b2	4b3	6b3	8b5	10b6	…

Отсюда мы получаем сначала соотношения 2b₂ = 2, 4b₃ = 2b₂, 6b₃ = 2b₃ + , …, а затем значения для

n = 1, 2, 3, 4, 5, 6, …

404

40. Вообще,

Этим можно воспользоваться для контроля вычислительной работы в примерах 38 и 39:

41.

Теперь вычислите интеграл, с которого мы начали (= (π/2)²/2) и воспользуйтесь примером 40. Ср. Euleer, Opera Omnia, ser. 1, vol. 14, p. 178—181.

42.

Теперь вычислите интеграл, с которого мы начали (=(π/2)³/3). Разложение (arcsin x)², которым мы воспользовались будет выведено в примере 5.1. Ср. Euleer, Opera Omnia, ser. 1, vol. 14, p. 181—184.

43. (a)

проинтегрируйте по частям, а затем введите в качестве новой переменной интегрирования s = 1—t.

(b) x = ½, которое делает большее из двух значений x и 1 — x насколько можно малым.

405

44. Если P_n(x) = 0, то мы имеем

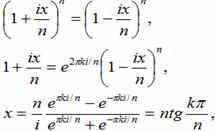
где мы берем k = 0, 1, 2, …, n — 1, если n нечетное.

45. Если n нечетное, то мы можем взять в выражении корней (см. пример 44)

k = 0, ± 1, ± 2, …, ± (n — 1)/2.

Следовательно,

Заметьте, что для фиксированного k

Для того чтобы перейти от достигнутого теперь пункта к доказательству, приемлемому с точки зрения современных стандартов, нужен лишь сравнительно небольшой шаг. Несколько другое построение рассуждения Эйлера, принадлежащее Коши, по-видимому, послужило в качестве модели Абелю, когда он, руководствуясь аналогией, открыл представление эллиптических функций в виде бесконечных произведений. Ср. Cauchy A., Œuvres complètes, ser. 2, vol. 3, p. 462—465, и Abel N. H., Œuvres complètes, vol. 3, p. 335—343.

46. Сумма конечного числа членов одна и та же, в каком бы порядке ни были взяты эти члены. Было бы ошибкой некритически распространить это утверждение на бесконечное число членов, т. е. допустить, что сумма бесконечного ряда одна и та же, в каком бы порядке ни были взяты члены. Допущенное утверждение неверно; что оно неверно, показывает наш пример. Предохранение от такой ошибки состоит в том, чтобы обратиться к определениям терминов, которыми мы пользуемся, и полагаться только на строгие доказательства, основанные на этих определениях. Так, сумма бесконечного ряда по определению есть предел некоторой последовательности (последовательности «частных сумм»), а переставляя бесконечное множество членов, что мы делали, мы существенно изменяем определяющую последовательность. (При некотором ограничительном условии перестановка членов бесконечного ряда не изменяет его суммы; см. Харди Г. Х., Курс чистой математики, М., 1949, стр. 346, 376, 380. Однако это условие в настоящем случае не удовлетоворяется.)

Нет решения: 5, 7, 9, 10, 11, 18, 19, 20, 21.

ГЛАВА III

1. Да. Г = 2n, В = n + 1, Р = 3n.

2. (1) Да: Г = m (p + 1), В = pm + 2, Р = m (p + 1) + pm; (2) p = 1, m = 4.

3. (1) Исключите на время тетраэдр; остальные шесть многогранников образуют три пары. два многогранника, входящие в одну и ту же пару, например куб и октаэдр, связаны таким образом, что у них одно и то же Р, но Г одного многогранника равно В другого. Тетраэдр остается в одиночестве, но он не связан

406

этим специфическим образом с самим собой. (2) Возьмите куб. возьмите две соседние грани куба и соедините их центры прямой. Таким путем получаем 12 прямых, образующих ребра правильного октаэдра. Этот октаэдр вписан в куб, шесть его вершин лежит в центрах шести граней куба. Наоборот, центры восьми граней правильного октаэдра являются восемью вершинами куба, вписанного в октаэдр. Подобная же взаимная связь имеет место между многогранниками, принадлежащими к одной паре и в других случаях. (Для додекаэдра и икосаэдра воспользуйтесь картонными моделями.) Тетраэдр имеет эту специфическую связь с самим собой: центры его четырех граней являются вершинами вписанного тетраэдра. (3) Переход от одного многогранника произвольной пары к другому сохраняет формулу Эйлера.

4. Сфера делится P красными граничными линиями на Г стран; существует В точек, принадлежащих границе более чем двух стран. Выберите в каждой стране точку, «столицу» страны. Соедините столицы любых двух соседних стран «дорогой» так, чтобы каждая дорога пересекала лишь одну граничную линию и различные дороги не пересекались между собой; нарисуйте эти дороги синим. Имеется точно Р синих линий (дорог), они деля сферу на Г' стран с В' точками, принадлежащими границе трех или более из этих стран. Убедитесь, что В' = Г и Г' = В. Связь между красным и синим подразделениями сферы взаимна, переход от одного к другому сохраняет формулу Эйлера.

5. Формула Эйлера имеет место после «пристройки крыши» «§ 4) в том и только в том случае, если она имела место до пристройки крыши. Но, пристраивая крыши ко всем нетреугольным граням данного многогранника, мы получаем другой многогранник, имеющий только треугольные грани.

6. Аналогично примеру 5: «усечение» вводит вершины с тремя ребрами, как «пристройка крыши» вводит треугольные грани. Мы могли бы также свести этот случай к примеру 5, пользуясь примером 4.

7. (1) N₀ = В, N₁ = Р, N₁ = Р, N₂ = Г — 1. Индексы 0, 1, 2 указывают соответствующую размеренность, см. § 7. (2) N₀ — N₁ + N₂ = 1.

8. (1) Положите l + m = c₁, lm = c₂. Тогда

N₀ = (l + 1) (m + 1) = 1 + c₁ + c₂,

N₁ = (l + 1) m + (m + 1) l = c₁ + 2c₂,

N₂ = lm = c₂.

(2) Да, N₀ — N₁ + N₂ = 1, хотя это простое разбиение прямоугольника не может быть получено в точности так, как в примере 7.

9. N₂·180° = (N₀ — 3)·360° + 180° Пытаясь ближе подойти к нашей цели, которой является равенство (2) в решении примера 7, последовательно преобразуем это равенство так:

2N₀ — N₂ — 0,

2N₀ — 3N₂ + 2N₂ — 3 = 2.

Подсчитывая число ребер двумя различными способами, получаем

3N₂ = 2N₁— 3.

Последние два равенства дают

N₀ — N₁ + N₂ = 1,

что, согласно примеру 7 (2), доказывает формулу Эйлера.

10. (1) Пусть l + m + n = c₁, lm + ln + mn = c₂ и lmn = c₃. Тогда

N₀ = (l + 1) (m + 1) (n + 1) = 1 + c₁ + c₂ + c₃,

N₁ = l (m + 1) (n + 1) + m (l + 1) (n + 1) + n (l + 1) (m + 1) = + c₁ + 2c₂ + 3c₃,

N₂ = (l + 1) mn + (m + 1) ln +(n + 1) lm = c₂ + 3c₃,

N₃ = lmn = c₃.

407

(2) Да, N_{0 —} N₁ + N₂ — N₃ = 1.

11. Со случаем n = 3 мы имели дело в § 16. Рассматривая этот случай, мы не пользовались никаким упрощающим обстоятельством, специфичным для частного случая n = 3. Следовательно, этот частный случай хорошо может «представлять» общий случай (в смысле примера 2.10), на что мы намекали уже в § 17. Читателю следовало бы повторить рассуждение из § 16, заменяя 3 на n, 4 на n + 1, 7 на L_n и 11 на L_n+1 с некоторой осторожностью. См. также пример 12.

12. Следуйте советам § 17 и аналогии с примером 11. Пусть даны n плоскостей, находящихся в общем положении. Они разбивают пространство на S_n частей. Добавьте еще одну плоскость; она пересекается предыдущими n плоскостями по n прямым, которые, находясь в общем положении, определяют на ней L_n областей. Каждая такая плоская область действует как «диафрагма»; она разбивает каждую старую часть (одну из упомянутых S_n частей) на две новые части, уничтожает одну старую часть и создает две новые части и, таким образом, в конечном счете добавляет к прежнему числу S_n частей единицу. Отсюда получается соотношение, которое мы хотели доказать.

13. См. третий столбец таблицы в § 14.

14. Второй столбец таблицы в § 14 находится в согласии с формулой

мы воспользовались обычным обозначением для биномиальных коэффициентов.

15. Конечных 3, бесконечных 8.

16. Пусть L_n^∞ обозначает число бесконечных частей среди L_n частей, определенных в примере 11. по наблюдениям, для

n = 1, 2, 3

L_n^∞ = 2, 4, 6.

Догадка: L_n^∞ = 2n. Доказательство: Возьмите точку в одной из конечных частей и представьте себе постоянно возрастающий круг с центром в этой точке. Когда этот круг становится очень большим, L_n = L_n^∞ конечных частей практически совпадает с его центром. Далее, n различных прямых, проходящих через центр круга, пересекают окружность в 2n точках и делят ее на 2n частей. Поэтому действительно L_n^∞ = 2n,

Например ответ в случае примера 15 таков:

1 — 1 — 4 + 6 = 3.

17. Так же, как пример 18, по аналогии с решением примера 16.

18. Так же, как пример 19.

19. См. пример 20.

20. Рассмотрим n окружностей на плоскости, любые две из которых пересекаются, в общем положении. Число частей, на которые эти окружности делят плоскость, принимая во внимание примеры 17, 18 и 19, обозначим символом S_n^∞. По аналогии с § 16 заметьте, что число частей, на которые окружность делится n

408

окружностями, ее пересекающими (предполагается общее положение), равно 2n. Найдите (пользуясь всеми тремя интерпретациями S_n^∞):

n	=	1	2	3	4,
2n	=	2	4	6	8,
Sn^∞	=	2	4	8	14

Догадка: S^∞_{n + 1} = S_n^∞ + 2n. Доказательство: как примеры 11, 12. Например,

S₅^∞ = S₄^∞ + 8 = 14 + 8 = 22.

Это решение примеров 17, 18 и 19. Дальнейшие догадки:

21. См. примеры 22—30.

22. Ненормально: Г = 1, В = Р = 0, 1 + 0 ≠ 0 + 2.

23. Ненормально: Г = 2, В = 0, Р = 1, 2 + 0 ≠ 1 + 2.

24. Ненормально: Г = 3, В = 2, Р = 3, 3 + 0 ≠ 2 + 2.

25. Нормально: Г = 3, В = 2, Р = 3, 3 + 2 = 3 + 2.

26. Ненормально: Г = p + 1, В = 0, Р = p, (p + 1) + 0 ≠p + 2; см. примеры 22, 23, 24 соответственно для случаев p = 1, 2, 3. Заметьте, что в настоящем случае решение примера 2 (1) становится неприменимым.

27. Случай m = 3, p = 0 нормален, см. пример 25, и нормальным же, но более общим является случай m ≥ 3, Г = m, В = 2, Р = m, m + 2 = m + 2. Случай m = 0, p = 0 ненормален, см. пример 22. остающиеся два случая можно интерпретировать так, что они окажутся нормальными. (1) m = 1, p = 0: одна страна с внутренней перегородкой, имеющей два конца. Г = 1, В = 2, Р = 1, 1 + 2 = 1 + 2. (2) m = 2, p = 0: две страны, отделенные двумя дугами и двумя углами, Г = 2, В = 2, Р = 2, 2 + 2 = 2 + 2. Более очевидная интерпретация, данная в примере 23, приводит к ответу: «ненормально». С настоящей интерпретацией решение примера 2 (1) остается применимым к случаю m > 0, p = 0.

28. m ≥ 3, p ≥ 1. Доказательство использует тот факт, что в любом выпуклом многограннике у каждой грани по крайней мере три ребра и в каждой вершине пересекаются по крайней мере три ребра.

29. Примеры 22—28 наталкивают на мысль о двух условиях: (1) Страна засчитываемая в Г в качестве грани выпуклого многогранника, должна быть «типа круга»; ни полная сфера, ни кольцо не принадлежат к этому типу. (2) Линия, засчитываемая в Р в качестве ребра выпуклого многогранника, должна оканчиваться в углах; полная окружность так не оканчивается (она не оканчивается вовсе). Пример 22 не удовлетворяет (1), пример 23 не удовлетворяет (2), пример 24 не удовлетворяет ни (1), ни (2), пример 25 или более общий случай m > 0, p = 0, интерпретированный так же, как в решении примера 27, удовлетворяет и (1), и (2), интерпретированный так же, как в решении примера 27, удовлетворяет и (1), и (2).

30. (1) Возьмите случай (3, 2) примера 2 (1), ср. пример 26, но сотрите на каждом меридиане дугу между двумя параллелями: Г = 7, В = 8, Р = 12, 7 + 8 ≠ 12 + 2; в этом случае среди стран есть сферическая зона, и, следовательно, имеется противоречие с условием (1), но не с условием (2) примера 29. (2) Случай Г = 1, В – 1, Р = 0 (одна страна, содержащая всю сферу, за исключением математической точки в северном полюсе); этот случай нормален, 1 + 1 = 0 + 2, но противоречит (1) или (2) примера 29 и т. д.

32. 3Г₃ + 4Г₄ + 5Г₅ + … = 3В₄ + 4В₄ + 5В₅ + … = 2Р.

33. Соответственно 4π, 12π, 8π, 36π, 20π.

34. ∑ = πГ₃ + 2πГ₄ + 3πГ₅ + …

409

35. На основании примеров 34, 32, 31

∑α = π∑(n — 2)Г_n = 2π (Р — Г).

36. Выпуклый сферический многоугольник с n сторонами может быть разбит на n — 2 сферических треугольника. Следовательно,

A = α₁ + α₂ + … + α_n — (n — 2) π = 2π — (π — α₁) —(π — α₂) — … — (π — α_n) = 2π — a′₁ — a′₂ — … — a′_n = 2π — P′.

37. Грани многогранника, проходящие через одну из его вершин, заключают внутренний телесный угол; его дополнение Декарт называет внешним телесным углом. Опишите вокруг этой вершины как центра шар радиуса 1, но сохраните только тот сектор шара, который содержится во внешнем телесном угле; полученные таким образом в отдельных вершинах многогранника секторы образуют, если их сдвинуть вместе, полный шар, как в аналогичной плоской фигуре (рис. 3.7) круговые секторы, если их сдвинуть вместе, образуют круг. Мы рассматриваем в качестве меры телесного угла площадь соответствующего сферического многоугольника: общая мера всех внешних телесных углов многогранника действительно равна 4π.

38. Пусть P₁, P₂, …, P_В обозначают периметры сферических многоугольников, соответствующих В внутренним телесным углам многогранника. Тогда в силу примеров 36 и 37

∑α = P₁ + P₂ + … + P_В = 2π — A′₁ + 2π — A′₂ + … +2π — A′_В = 2πВ — 4π.

39. На основании примеров 35 и 38

2π(P — Г) = ∑α = 2π(В — 2).

40. На основании примеров 31, 32

3Г = 3Г₃ + 3Г₄ + 3Г₅ + … ≤ 3Г₃ + 4Г₄ + 5Г₅ + … = 2Р,

что дает первое из шести предложенных неравенств. Случай равенства достигается, когда Г = Г₃, т. е. когда все грани являются треугольниками. Исключая из формулы Эйлера и только что доказанного неравенства сначала Р, а затем Г, получаем остальные два неравенства в первой строке; они переходят в равенства в том и только в том случае, если все грани являются треугольниками. Меняя роли Г и В, как указано в примерах 3 и 4, получаем три предложенных неравенства во второй строке; они переходят в равенства в том и только в том случае, если все вершины многогранника являются трехреберными. Некоторые из доказанных неравенств содержится в заметках Декарта.

41. Из теоремы Эйлера получаем

6Г — 2Р = 12 + 2 (2Р — 3В).

а отсюда на основании примеров 31, 32 и 40

3Г₃ + 2Г₄ + Г₅ = 12 + 2(2Р — 3В) + Г₇ + 2Г₈ + …, 3Г₃ + 2Г₄ + Г₅ ≥ 12,

и, таким образом, любой выпуклый многогранник должен иметь грани с менее чем шестью сторонами.

Нет решения: 31.

410

ГЛАВА IV

1. R₂ (25) = 12, см. § 2; S₃ (11) = 3.

2. R₂ (n) обозначает число точек решетки на плоскости, лежащих на окружности радиуса √͞n с центром в начале координат. (Возьмите случай n = 25, пример 1, и начертите окружность.) R₃ (n) есть число точек решетки в пространстве на сфере радиуса √͞n с центром в начале координат.

3. Если p — нечетное простое число, то R₂ (p²) = 12 или 4 в зависимости от того, дает ли p при делении на 4 остаток 1 или 3.

4. Сравнение таблиц наводит на мысль: если p — нечетное простое число, то или и p, и p² представимы как суммы двух квадратов или же ни p, ни p² не представимы. Нашими наблюдениями также несколько подкрепляется более точное предположение: если p — нечетное простое число, то R₂ (p) = 8 или 0, в зависимости от того, дает ли p при делении на 4 остаток 1 или 3.

5. Если p = x² + y², то

p² = x⁴ + 2 x²y² + y⁴ = (x^{2 —} y²)² + (2xy)²,

т. е. если R₂(p) > 0, то и R₂(p²) > 0. Это лишь половина нашего менее точного и лишь небольшая часть нашего более точного предположения. (если мы знаем, что R₂(p²) > 0, то заключение относительно R₂(p) > 0 определенно менее очевидно.) Тем не менее кажется разумным, что такое частичное подтверждение значительно усиливает нашу уверенность в менее точном предположении и, кроме того, несколько усиливает нашу уверенность в более точном предположении.

6. R₃(n) = 0 для n = 7, 15, 23 и 28 и ни для каких других n до 30; см. табл. II на стр. 94, 95.

7. Вот соответствующие взносы в S⁴ (n): (1) 24; (2) 12, (3) 6, (4) 4, (5) 1.

8. Во-первых, следует сослаться на случаи, выделенные в примере 7. Если S₄ (4u), нечетно, то необходимо возникает случай (5) и, таким образом,

4u = a² + a² + a² + a² +,

u = a².

Во-вторых, любому делителю d числа u соответствует делитель u/d, и эти два делителя, если u не равно d², различны. Поэтому число делителей u нечетно или четно в соответствии с тем, является ли u квадратом или нет, и это же имеет место для суммы этих делителей, так как, когда нечетно само u, каждый делитель u нечетен. В § 6 мы высказали предположение, что S₄ (4u) и сумма делителей числа u равны; мы доказали теперь, что эти два числа дают при делении на 2 один и тот же остаток. Доказав часть нашего предположения, мы должны, конечно, больше в него верить.

9.

10. См. табл 11, стр. 94, 95. Проверьте по крайней мере несколько чисел. Из примера 9 следует, что R₄(n) делится на 8.

11. Попытка подметить хотя бы отрывочные закономерности (подобная той, которую мы делали в § 6) может привести вас к следующей группировке более бросающихся в глаза случаев:

(1) 2 3 5 7 11 13 17 19 23 29

3 4 6 8 12 14 18 20 24 30

411

(2) 2 4 8 16

3 3 3 3

(3) 4 8 12 16 20 24 28

3 3 12 3 18 12 24

В (1), (2) и (3) первая строка дает n, вторая строка R₄(n)/8.

12. Сделано в решении примера 11: (1) простые числа, (2) степени числа 2, (3) числа, делящиеся на у.

13. По аналогии с § 6 и с помощью небольшого наблюдения сравнительно легко открыть закон, когда n не делится на 4. поэтому мы сосредоточим внимание на случае (3) в решении примера 11.

n =	4	8	12	16	20	24	28
n/4 =	1	2	3	4	5	6	7
R4(n)/8 =	3	3	12	3	18	12	24

Число в третьей строке, напечатанное жирным шрифтом, является суммой всех делителей соответствующего числа из второй строки и, следовательно, суммой некоторых делителей соответствующего числа из первой строки, которая нас в действительности и интересует. Эти наблюдения приводят нас к другому испытанию:

n	=	4	8	12	16
R4 (n)/8	=	1 +2	1 + 2	1 + 2+ 3 + 6	1 + 2
n	=	20		24	28
R4 (n)/8	=	1 + 2+ 5 + 10		1 + 2+ 3 + 6	1 + 2+ 7 + 14

Какие делители складываются? Какие делители отбрасываются?

14. R₄(n), число представлений n в виде суммы четырех квадратов, равно восьмикратной сумме тех делителей n, которые не делятся на 4. (Если само n не делится на 4, то и ни один из его делителей не делится на 4 и потому в этом чаще встречающемся случае правило проще.)

15. Соответственно столбцам табл. II:

31	25 + 4 + 1 + 1	12 × 16	32 = 31 + 1
	9 + 9 + 9 + 4	4 × 16
32	16 + 16	6 × 4	3 = 2 + 1
	25 + 4 + 4	12 × 8	48 = 33 + 11 + 3 + 1
33	16 + 16 + 1	12 × 8
	16 + 9 + 4 + 4	12 × 16

16. 5 = 1 + 1 +1 +1 +1 = 4 + 1,

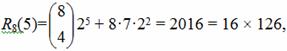
40 = 25 + 9 + 1 + 1 + 1 + 1 + 1 +1,

40 = 9 + 9 + 9 + 9 + 1 + 1 + 1 +1,

17. Пример 16. Таблица III в действительности была составлена с помощью метода менее трудоемкого, чем метод примера 16; ср. примеры 6.17 и 6.23.

412

18. В пределах табл III и R₈ (n) и S₈ (8n) монотонно возрастают вместе с n, тогда как R₄ (n) и S₄ (4(2n — 1)) неправильно колеблются.

19. Аналогия с R₄ (n) и S₄ (4(2n — 1)) указывает на делители; одну отрывочную закономерность легко заметить: если n нечетно, то R₈ (n)/16 и S₈ (8n) в точности равны; если n нечетно, то они различны, хотя различие в большей части случаев сравнительно невелико.

20. Нечетные и четные — в примере 19. степени числа 2:

n	1	2	4	8	16
S8 (8n)	1	8	64	512	4096

И вторая строка состоит из степеней числа 2:

n	2^0	2^1	2^2	2^3	2^4
S8 (8n)	2^0	2^3	2^6	2^9	2^12

Каков закон показателей степени?

21. Если n — степень числа 2, то S₈ (8n) — n³. это [и монотонное возрастание R₈ (n) и S₈ (8n)] подводит к составлению следующей таблицы

n	R8(n)/16 S8 (8n) —	n^3
1	0	0
2	—1	0
3	1	1
4	7	0
5	1	1
6	—20	8
7	1	1
8	71	0
9	28	28
10	—118	8
11	1	1
12	260	64
13	1	1
14	—336	8
15	153	153
16	583	0
17	1	1
18	—533	224
19	1	1
20	946	64

В столбце, относящемся к R₈(n), знаки + и — распределяются закономерно

413

22. Кубы делителей!

n	R8(n)/16 = S8 (8n)
1	1^3
3	3^3 + 1^3
5	5^3 + 1^3
7	7^3 + 1^3
9	9^3 + 3^3 +1^3
11	11^3 + 1^3
13	13^3 + 1^3
15	15^3 + 5^3+ 3^3 +1^3
17	17^3 + 1^3
19	19^3 + 1^3

n	R8(n)/16	S8 (8n)
2	2^3 — 1^3	2^3
4	4^3 + 2^3 — 1^3	4^3
6	6^3 — 3^3 + 2^3 — 1^3	6^3 + 2^3
8	8^3 + 4^3+ 2^3 + 1^3	8^3
10	10^3 — 5^3+ 2^3 — 1^3	10^3 + 2^3
12	12^3 + 6^3 +4^3 — 3^3 + 2^3 — 1^3	12^3 + 4^3
14	14^3 — 7^3 + 2^3 — 1^3	14^3 + 2^3
16	16^3 + 8^3 + 4^3 + 2^3 — 1^3	16^3
18	18^3 — 9^3 + 6^3 — 3^3 + 2^3 — 1^3	18^3 + 6^3 + 2^3
20	20^3 + 10^3 — 5^3 + 4^3 + 2^3 — 1^3	20^3 + 4^3

23. (1) (— 1)^n—1R₈(n)/16 равно разности суммы кубов всех нечетных делителей n и суммы кубов всех четных делителей n. (2) S₈(8n) равно сумме кубов тех делителей n, дополнительные множители которых нечетны. (Если d — делитель n, то мы называем дополнительным множителем d число n/d.) По поводу истории этих теорем и для ссылок см. пример 6.24.

24. Составьте таблицу

0	3	6	9	12
5	8	11	14
10	13

Которую следует себе представлять как неограниченно продолжающуюся вниз и вправо. Она показывает, что единственными положительными целыми числами, не выражающимися в указанном виде, являются 1, 2, 4, 7.

25. Случай a = 3, b = 5 в примере 24; a и b — взаимно простые числа. Последнее целое число, не выражающееся в указанном виде, ab — a — b = (a + 1) × (b — 1) — 1. Это несравненно легче, чем законы, относящиеся к суммам квадратов.

26. (1) верно всегда, (2) верно не всегда, но первым исключением является n = 341. (См. Hardy G. H. and Whright E. M., An introduction to the theory of numbers, Oxford, 1938, p. 69, 72.)

414

ГЛАВА V

1. [Ср. Путнэм 1948.]

(b) Убедившись, что y удовлетворяет указанному дифференциальному уравнению, положите

y = a₀x + a₁x³ + a₂x⁵ + … a_nx²ⁿ⁺¹ + …

Для сравнения коэффициентов при одинаковых степенях можно воспользоваться таблицей

		x^2	x^4	…	x^2n	…
y'	a0	3a1	5a2	…	(2n +1) an	…
—x^2y'		— a0	— 3a1	…	— (2n — 1) an—1	…
—xy		— a0	— a1	…	an—1	…
	1	0	0	…	0	…

Которая дает a₀ = 1 и (2n +1) a_n = 2na_n—1 для n ≥ 1.

2. [Ср. Путнэм 1950.]

(b) Так как

то это разложение удовлетворяет уравнению

y' = 1 + xy.

Данное произведение y удовлетворяет тому же самому дифференциальному уравнению. И разложение, и произведение обращаются в нуль, когда x = 0. Следовательно, они тождественны.

3. Соотношения между коэффициентами a_n, выведенные из формулы

показаны в таблице (см. пример 1).

1	— 1	1	— 1	1
	4a1	— 4a1·3	4a1·6	4a1·10
		16a2	— 16a2·5	16a2·15
			64a3	— 64a3·7
				256a4
1	0	a1	0	a2

Они дают

Этот пример представляет исторический интерес. См. Gauss, Werke, V. 3, S.

415

4. Изучите строение следующей таблицы (см. примеры 1, 3):

f (x)^3	{	a0^³	3a1a0^²	3a2a0^²	3a3a0^²	3a4a0^²
				3a1^²a0	6a2a1a0	6a3a1a0
					a1^3	3a2^2a0
						3a2a1^2
3f (x) f (x^3)	{	3a0^²	3a1a0	3a2a0	3a3a0	3a4a0
				3a0a1	3a1a1	3a2a1
						3a0a2
2f (x^3)		2a0			2a1
		6a1	6a2	6a3	6a4	6a5

Начиная с a₀ = 1, последовательно получим a₁, a₂, a₃, a₄ и a₅ = 8. См.: Pólya G., Zeitschrift für Kristallographie, (A) 93 (1936), 415—443, и Acta Mathematica, 68 (1937), 145—252.

5. Из сравнения разложений в § 1.

6. (a) ε²/15. (b) + ∞. В обоих крайних случаях погрешность положительна, приближенное значение больше, чем истинное значение.

7. (a) ε²/15. (b) ⅓. В обоих крайних случаях приближенное значение больше, чем истинное значение.

8. 4π (a² + b² + c²)/3. Есть некоторое основание подозревать, что это приближение дает значение, превосходящее истинное значение. См.^ Pólya G., Publicationes del Instituto di Matematica Posario, 5 (1943).

9. При переходе от интеграла к ряду воспользуйтесь биномиальным разложением и интегральными формулами примера 2.42.

10. Воспользуйтесь решением примера 9 и положите Тогда g₁ > g_n для n ≥ 2 и для ε > 0

11. Начальный член относительной погрешности для P″ равен

—[α + 3(1 — α)] ε/64 + …,

и, таким образом, он имеет порядок 4, если α ≠ 3/2 и P″ ≠ P + (P — P′)/2.

12. (P″ — E)/E = 3·2^–14ε⁸ + …, когда ε мало,

= (3π — 8)/8 = 0,1781, когда ε =1,

= 0, 00019, когда ε = 4/5

Отсюда предположение P″ > E. См.: Peano G., Applicazioni geometriche del calcolo infinitesimale, p. 231—236.

416

13.

Следовательно, желательное заключение эквивалентно

Противоположное допущение означает, что

для n > N, где N — некоторый фиксированный номер, или, что то же самое,

Рассмотрим значения n = (m — 1)p:

Как и в § 5, заключаем, что для подходящей постоянной C

и это при m → ∞ приводит к противоречию с предположением a_n > 0.

14. Пример a_n = n^c из § 4 подсказывает:

a₁ = 1, a_n = n ln n для n = 2, 3, 4,…

При этом выборе

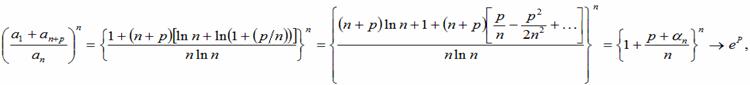
так как α_n → 0.

15. Рассматриваемые мантиссы — это 900 ординат медленно возрастающей кривой y = lg x — 2, соответствующие абсциссам x = 100, 101, …, 999; знак lg обозначает десятичный логарифм. Таблица I указывает, сколько из этих 900 точек на кривой попадает в определенные горизонтальные полосы ширины 1/10. Рассмотрим точки, в которых эта кривая входит и выходит из такой полосы. Если x_n — абсцисса такой точки, то

lg x_n — 2 = n/10, x_n = 100·10^n/10,

где n = 0, 1, 2, …, 10. Число целых чисел в любом интервале приблизительно равно длине интервала: разность меньше единицы. Поэтому число рассматрива-

417

емых мантисс, имеющих первой цифрой n, приближенно равно x_n+1 — x_n, причем ошибка меньше, чем 1. Теперь

x_n+1 — x_n = 100 (10^1/10 — 1) 10^n/10

есть n-й член геометрической прогрессии со знаменателем

10^1/10 = 1,25893.

Предскажите и подметьте аналогичное явление в шестизначной таблице десятичных логарифмов.

16. Периодическое повторение может (и должно) рассматриваться как своего рода симметрия; но оно имеется во всех случаях, и поэтому мы не будем его больше упоминать. В нашей классификации играют роль следующие типы симметрии:

(1) Центр симметрии. Обозначение: ц, ц′.

(2) Ось симметрии. Обозначение: г, если эта ось горизонтальна, в или в′, если она вертикальна.

(3) Скользящая симметрия: если передвинуть фриз горизонтально и одновременно отразить относительно ценьтральной горизонтальной прямой, то он совпадет сам с собой (в фризах 5, 7, а, б). Обозначение: с.

На рис. 5.2 представлены следующие типы симметрии (Штрих ′ применяется для того, чтобы отличить два элемента симметрии одного и того же типа, например, ц и ц′ или в и в′, когда их положение на фигуре существенно различно.)

1, d: нет симметрии (исключая периодичность)

2, g: ц, ц′, ц, ц′, …

3, f: в, в′, в, в′, …

4, e: г

5, a: с

6, c: г; (в, ц), (в′, ц′), (в, ц), (в′, ц′), …

7, b: с; в, ц, в, ц, …

На рис 5.2 представлены все возможные типы симметрии, в чем вы можете убедиться с помощью индукции.

17. Представлены три различных типа симметрии: 1 имеет тот же тип, что и 2, 3 — что и 4. Попытайтесь найти все типы. Ср.: Pólya G., Zeitschrift für Kristallographie, 60 (1924), 278—282, Niggli P., там же, 283—298, Г. Вейль, Симметрия, М., 1968.

18. Пренебрегите деталями, зависящими от особенностей шрифта (1) вертикальная ось симметрии, (2) горизонтальная ось симметрии, (3) центр симметрии, (4) все три предыдущих типа симметрии вместе, (5) нет симметрии. То же самое для пяти кривых, представляющих в прямоугольных координатах пять уравнений. Каким-нибудь вариантом этой задачи можно воспользоваться, чтобы оживить занятия по аналитической геометрии.

ГЛАВА 6

2. x(1 — x)². Частный случай примера 3 при f(x) = (1 — x)^–1; получите его также комбинируя примеры 4 и 5.

3.

4.

5.

6.

418

7. D₃ = 1, D₄ = 2, D₅ = 5, D₆ = 14. Для случая D₆ обратитесь к рис 6.1; существует 2 различных разбиения типа I, 6 типа II и 6 типа III.

8. Рекуррентная форма подтверждается для n = 6:

14 = 1 × 5 + 1 × 2 + 2 × 1 + 5 × 1.

Выберите определенную сторону в качестве основания многоугольника (на рис 6.2 горизонтальная сторона) и начните разбиение, проведя вторую и третью стороны треугольника Δ, первой стороной которого является основание. Когда выбран Δ, вам еще остается разбить многоугольник с k сторонами слева от Δ и другой многоугольник с n + 1 — k сторонами справа; оба эти многоугольника вместе дают D_kD_{n + 1 – k} возможностей. Выберите k = 2, 3, 4, …, n — 1; конечно, вы должны подходящим образом интерпретировать случай k = 2.

9. В силу примеров 4 и 6 рекуррентная формула для D_n дает

xg(x) = D₂x³ + [g(x)]².

Разлагая эту функцию и пользуясь обозначениями для биномиальных коэффициентов, вы найдете:

10. Лучше так:

где u, v и w независимо пробегают все целые числа (от – ∞ до + ∞), так что тройная сумма распространена на все точки решетки пространства (см. пример 4.2). чтобы увидеть, что это — производящая функция для R₃ (n), соберите только те члены, показатель степени u² + v² + w² которых имеет одно и то же значение n.

11.

12.

13. Пусть I, J, K и L обозначают некоторые степенные ряды, все коэффициенты которых являются целыми числами. Тогда производящие функции для R₁(n), R₂(n), R₄(n) и R₈(n) соответственно имеют вид

1 + 2I,

(1 + 2I)² = 1 + 4J,

(1 + 4J)² = 1 + 8K,

(1 + 8K)² = 1 + 16L.

14. x + x⁹ + x²⁵ + x⁴⁹ + x⁸¹ + … = x(1 + x⁸ + x²⁴ + x⁴⁸ + x⁸⁰ + …) = xP,

Где P обозначает степенной ряд, у которого коэффициент при xⁿ обращается в нуль, когда n не делится на 8. Производящие функции для

S₁(n), S₂(n), S₄(n), S₈(n),

соответственно, будут

xP, x²P², x⁴P⁴, x⁸P⁸.

419

15. На основании примеров 6 и 11,

G^{k + l} = G^k·G^k,

где G обозначает производящую функцию для R₁(n).

16. Аналогично примеру 15, на основании примеров 6 и 12.

17. Воспользуйтесь примерами 15и 16 при k = l = 4. Фактические вычисления производились по этому методу со случайными проверками по другим источникам, как примеры 4, 16 и 23.

18. (1) Из примеров 14 и 16 следует

S₄(4)S₄(8n — 4) + S₄(12)S₄(8n — 12) + … + S₄(8n — 4)S₄(4) = S₈(8n).

В § 4.6 было сделано предположение, что S₄(4(2n — 1)) = σ(2n — 1), а в примере 4.23, — что S₈(8u) = σ₃(u)если u — нечетное число.

(2) σ(1)σ(9) + σ(3)σ(7) + σ(5)σ(5) + σ(7)σ(3) + σ(9)σ(1) = 2 (1 × 13 + 4 × 8) + 5 × 6 =

= 126 = 5³ + 1³ = σ₃(5).

(3) Кажется разумным, что такое подтверждение до некоторой степени увеличивает нашу веру в оба предположения.

19.

для u = 1¸3, 5, …; суммирование распространено на все неотрицательные целые числа, удовлетворяющие неравенству

0 ≤ k(k + 1) < u.

20. σ(3) = 4σ(1),

2σ(5) = 3σ(3),

3σ(7) = 2σ(5) + 12σ(1),

4σ(9) = σ(7) + 11σ(3)

Последнее верно, так как

4 × 13 = 8 + 11 × 4.

21. Рекуррентная формула для S₄(4(2n —1)) была доказана в примере 19. Эта рекуррентная формула в действительности дает бесконечную систему соотношений, однозначно определяющую S₄(4(2n —1)), если дано S₄(4). Далее, мы знаем, что

S₄(4) = σ(1) = 1.

Если (2n —1) удовлетворяет той же самой системе рекуррентных соотношений, что и S₄(4(2n —1)), то

S₄(4(2n —1)) = σ(1) = 1.

Если σ(2n —1) удовлетворяет той же самой системе рекуррентных соотношений, что и S₄(4(2n —1)), то

S₄(4(2n —1)) = σ(2n —1)

Для n = 1, 2, 3, …, потому что система однозначно определяет решение. Если, наоборот, выполняется последнее равенство, то σ(2n —1) удовлетворяет указанным рекуррентным соотношениям.

22. Допустим, что

G = a₀ + a₁x + a₂x² + a₃x³ + …, H = u₀ + u₁x + u₂x² + u₃x³ + …, G^k = H

Как и в примере 19, отсюда следует, что

GxH′ — kxG′H = 0

420

Приравняйте нулю коэффициент при xⁿ:

Рассмотрите a₀, a₁, a₂, … как данные. Из последнего равенства вы можете выразить u_n через u_n-1, u_n-2, …, u₁, u₀, если a₀ ≠ 0. заметьте, что u₀ = a₀^k.

23. Примените пример 22 к случаю k = 8,

G = 1 + 2x + 2x⁴ + 2x⁹+ 2x¹⁶ + …

В силу примера 11 результат примера 22 дает

nR₈(n) = 2(9 — n)R₈(n —1) +2(36 — n)R₈(n —4) +2(81 — n)R₈(n —90) + …

Положите R₈(n)/16 = r_n. Тогда r₀ = 1/16 и мы находим r₁, r₂, r₃, …, r₁₀, последовательно из равенств

r1 =	16r0,
2r2 =	14r1,
3r3 =	12r2,
4r4 =	10r3 + 64r0,
5r5 =	8r4 + 62r1,
6r6 =	6r5 + 60r2,
7r7 =	4r6 + 58r3,
8r8 =	2r7 + 56r4,
9r9 =	+ 54r5 + 144r0,
10r10 =	— 2r9 + 52r6 + 142r1.

Когда мы пользуемся этими формулами для вычислений, у нас есть хорошая возможность себя контролировать: правая часть уравнения, из которого мы получаем r_n, должна делиться на n.

Тот же метод дает рекуррентную формулу для R_k(n).

25. Обозначьте через s рассматриваемое бесконечное произведение. Вычисляя и пользуясь п. 10 мемуара Эйлера, вы получите

все три суммы берутся от 1 до ∞. Умножьте это равенство на знаменатель правой части и рассмотрите коэффициент при xⁿ.

В случае Эйлера k = 1. Случай k = 3 также дает сравнительно простой результат (см. Hardy G. H. and Wright E. M., An introduction to the theory of numbers. Oxford, 1938, p. 282, 283; теоремы 353 и 357). В других случаях у нас нет достаточных знаний о законе коэффициентов a_n.

Нет решения: 1. 24.

ГЛАВА VII

1. [Стэнфорд 1950].

Для перехода от n к n + 1 нужно убедиться в том, что

421

2. Чтобы доказать, что

мы пользуемся соответственно примером 3.11, примером 3.12 в соединении с выражением P_n и примером 3.20. Затем, допустив, что имеют место написанные выше равенства, мы должны убедиться в том, что

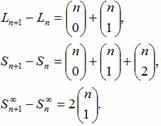
Все эти три равенства следуют из хорошо известного факта (основного соотношения треугольника Паскаля):

3. «Как решать задачу, стр. 92—98.

4.

Для перехода от n к n +1 нужно убедиться в том, что

Ср. пример 2.23.

5.

Для перехода от n к n +1 нужно убедиться в том, что

Ср. пример 2.31.

6. Общий случай в действительности эквивалентен предельному случаю

из которого предложенный частный случай выводится следующим образом: подставив x¹⁶ вместо x и умножив на 16, получим

422

затем нужно вычесть это равенство из первоначального. Если мы положим 2ⁿ⁺¹ = m, то переход от n к n +1 требует

7. Следует доказать

1 + 3 + 5 + 7 + … + 2n — 1 = n².

Для перехода от n к n +1 нужно убедиться в том, что

2n + 1 = (n + 1)² — n².

8. n-й член четвертой строки таблицы равен

(1 + 2) + (4 + 5) + … + (3n — 5 + 3n — 4) + 3n — 2 = 3 + 9 + … + [6 (n — 1) — 3] =

На самом деле переход от n —1 к n требует

n³ — (n —1)³ = 3n² — 3n + 1.

9. После n², n³, n⁴ обобщение, относящееся к n^k, очевидно. Просто случай n² был известен еще в древности; Альфред Месснер совсем недавно открыл остальные случаи с помощью эмпирической индукции, а Оскар Перрон доказал их с помощью математической индукции. См. Sitzungsberichte der Bayerischen Akademie der Wissenschaften, Math-naturwiss. Klasse, 1951, 29—43.

10. Для k = 1 теорема сводится к очевидному тождеству

1 — n = — (n — 1).

Для перехода от k к k + 1 нужно убедиться в том, что

но это — основное соотношение треугольника Паскаля, уже встретившееся в примере 2.

11 [Стэнфорд 1946]. Обозначим искомое число пар из 2n игроков символом P_n. n-й игрок может войти в пару с любым из остальных 2n — 1 игроков. Раз его противник выбран, остаются

2n — 2 = 2(n — 1)

игроков, из которых пары могут быть составлены P_n—1 способами. Поэтому

P_n = (2n —1) P_{n — 1}.

12. Обозначим символом A_n утверждение, которое предложено доказать, относящееся к f_n(x). Вместо A_n мы докажем A′_n:

Функция f_n(x) есть дробь, знаменатель которой равен (1 — x)ⁿ⁺¹, а числитель есть многочлен степени n, свободный член которого равен 0, а остальные коэффициенты являются целыми положительными числами.

Заметьте, что A′_n утверждает больше, чем A_n; пункты, в отношении которых A′_n идет дальше, чем A_n, выделены курсивом. Допустив, что имеет место A′_n, положим

(1 — n)^{n + 1}f_n(x) = a₁x + a₂x² + … + a_nxⁿ,

где a₁, a₂, a_n предполагаются положительными целыми числами. Из нашего рекуррентного определения мы выводим рекуррентную формулу.

P_n+1 (x) = x[(1—x) P′_n (x) + (n + 1) P_n (x)],

423

и это показывает, что коэффициенты при x, x ², x ³, …, x ⁿ и x ^{n + 1} в P_n+1 (x) соответственно равны a₁, na₁ + 2a₂, (n — 1) a₂ + 3a₃, …, 2n_n—1 + na_n, a_n, что делает наше утверждение очевидным.

13 (1) Сумма всех коэффициентов P_n (x) равна n!. В самом деле, эта сумма равна P_n (1), и рекуррентная формула дает

P_{n + 1} (1) = (n + 1) P_n (1).

(2) P_n (x)/ x есть возвратный многочлен, или

P_n (1/x) x ^{n + 1} = P_n (x).

В самом деле, допустим, что a₁ = a_n, a₂ = a_{n — 1}, … ; тогда соответствующие соотношения для коэффициентов многочлена P_n+1 (x) следуют из их выражений, данных в конце решения примера 12.

16. Q₁ = 1, Q₂ = 3, Q₃ = 45, Q₄ = 4725, Q₂/Q₁ = 3, Q₃/Q₂ = 15, Q₄/Q₃ = 105.

Значит,

Q_n = 1ⁿ1^{n —1}1^n—2 … (2n — 3)²(2n—1)¹

В самом деле, определение дает

и, таким образом, вы докажете общий закон с помощью умозаключения от n — 1 к n + 1. Заметьте, что

17. Рассуждение, которое привело нас от 3 к 4, годится для перехода от n к n + 1 с одним исключением: оно теряет силу при переходе от 1 к 2.

18. От n = 3 к n + 1 = 4; рассмотрим прямые a, b, c и d. Рассмотрим сначала случай, когда среди этих четырех прямых имеются хотя бы две различные прямые, например b и c. Тогда точка пересечения b и c однозначно определена и должна также лежать и на a (потому что, по предположению, наше утверждение имеет место для n = 3) и на d (по той же причине). Следовательно, утверждение верно для n + 1 = 4. Если, однако, все четыре прямые совпадают, то утверждение очевидно. Это рассуждение теряет силу, как это и должно быть, при переходе от 2 к 3.

Нет решения: 14, 15.

ГЛАВА VIII

1. (1) Отрезок прямой; (2) перпендикуляр; (3) общий перпендикуляр; (4) отрезки прямой, проходящей через данную точку и центр (Евклид III, 7, 8); (5) отрезок перпендикуляра, проходящего через центр, наибольшего расстояния нет; (6 отрезки прямой, соединяющей центры. Случай, когда наименьшее расстояние равно 0, в каждой задаче не принимался во внимание как очевидный, хотя он может быть важным.

2. (1) Отрезок прямой; (2) перпендикуляр; (3) общий перпендикуляр; (4) перпендикуляр; (5) общий перпендикуляр; (6) см. § 4; (7) отрезки прямой, соединяющей точку с центром; (8) отрезок перпендикуляра, проходящего через центр, наибольшего расстояния нет; (9) отрезок перпендикуляра, проходящего через центр, наибольшего расстояния нет; (10) отрезки прямой, соединяющей центры. Случай, когда наименьшее расстояние равно 0, не принимался во внимание.

3. (1) Концентрические окружности; (2) параллельные прямые; (3) концентрические окружности.

424

4. (1) Концентрические сферы; (2) параллельные плоскости; (3) цилиндры с общей осью; (4) концентрические сферы.

5. (2) См. § 3. Остальные аналогично.

6. (6) Существует точно один цилиндр, имеющий первую данную прямую своей осью и вторую данную прямую своей касательной. Точка касания есть конец отрезка, дающего наименьшее расстояние. Остальные аналогично.

7. Одну из данных сторон назовите основанием. Пусть основание остается в фиксированном положении, а вторая сторона вращается вокруг своего фиксированного конца. Обозначим другой ее конец буквой X. Предписанным путем X является окружность, линиями уровня — параллели к основанию, наибольшую площадь имеет прямоугольный треугольник (что очевидно).

8. Данную сторону назовите основанием, пусть она остается в фиксированном положении. Противоположную вершину обозначьте буквой X, и пусть X изменяется. Предписанным путем X является эллипс, линиями уровня — параллели к основанию, наибольшую площадь имеет равнобедренный треугольник.

9. Линии уровня — прямые x + y = const, предписанный путь — одна ветвь равнобочной гиперболы с уравнением xy = A, где A — данная площадь. Ввиду симметрии ясно, что есть точка касания с x = y.

10. Рассмотрите расширяющиеся концентрические окружности с центром в данной точке. Интуитивно кажется ясным, что существует первая окружность, достигающая данной линии; ее радиус является кратчайшим расстоянием. Это несомненно так в случаях примеров 1 (2) и (4).

11. Пересечение означает переход с одной стороны линии уровня на другую, а с одной стороны f принимает бо́льшие, с другой же — меньшие значения, чем в точке пересечения.

12. Можете, но не обязательно. Наиболее высокая точка может быть вершиной (вы можете захотеть поглядеть, каков вид с этой вершины) или перевалом (вы можете пересечь его, переходя из одной долины в другую) или начальной точкой вашего пути или его конечной точкой или его угловой точкой.

13. (1) Линия уровня для 180° — отрезок AB, линия уровня для 0° состоит из прямой, проходящей через точки A и B, исключая отрезок AB. Любая другая линия уровня состоит из двух дуг окружности, имеющих концы в точках A и B, и симметричных одна с другой относительно прямой, проходящей через A и B. (2) Если две линии уровня различны, то одна лежит внутри другой; ∠ AXB принимает бо́льшее значение на внутренней, а меньшее — на внешней линии уровня. При подходящей интерпретации это относится и к 0°

14. Минимум достигается в точке, где линия l пересекает прямую, проходящую через A и B, т. е. линию уровня. Это не противоречит принципу, сформулированному в примере 11; с обеих сторон от этой специальной линии уровня ∠ AXB принимает бо́льшие значения, чем на ней.

15. Обозначение, как в § 6. Оставим на время c постоянным. Тогда, так как V = abc/3 дано, то и ab будет постоянным и

S = 2ab + 2(a + b)c

Минимально, когда минимально 2(a + b), периметр прямоугольника с данной площадью ab. Это имеет место, когда a = b. Теперь измените вашу точку зрения и оставьте постоянным другое ребро.

16. Оставьте одну из сторон постоянной. Тогда вы имеете случай примера 8[275] и две другие стороны должны быть равны (треугольник равнобедренный. Это рассуждение можно применить к любым двум сторонам, и треугольник должен быть равносторонним.

17. Оставьте фиксированными плоскость основания и противоположную вершину, но изменяйте основание, являющееся треугольником, вписанным в данный круг. Высота постоянна; площадь основания (а вместе с ней и объем) становится наибольшей, когда основание есть равносторонний треугольник, в силу § 4 (2). В качестве основания мы можем выбрать любую грань, и, таким образом, когда достигается максимум объема, каждая грань должна быть равносторонним треугольником, а тетраэдр правильным.

425

18. Рассмотрите треугольник между a и b в качестве основания. Не изменяя соответствующей высоты, измените основание в прямоугольный треугольник; это изменение увеличивает площадь основания (пример 7) и, следовательно, объем. Вы могли бы теперь подобным же образом рассмотреть другую пару сторон, однако лучше сразу сделать c перпендикулярным и к a, и к b.

19. Фиксируя на цилиндре конец отрезка, дающего кратчайшее расстояние, вы найдете в силу примера 2 (7), что этот отрезок является перпендикуляром к сфере. Фиксируя его конец на сфере, вы можете убедиться, что этот отрезок перпендикулярен и к цилиндру. Следовательно, он должен быть перпендикулярен и к сфере, и к цилиндру. Это можно также показать и непосредственно.

20. Метод примера 19 показывает, что отрезок, дающий кратчайшее расстояние, должен быть перпендикулярен к обоим цилиндрам. В действительности он должен лежать на той же прямой, на которой лежит отрезок, дающий кратчайшее расстояние между осями цилиндров.

21. Метод примера 19 и аналог примера 10 в пространстве.

22. По предположению

f(X, Y, Z, …) ≤ f(A, B, C, …)

для всех допустимых значений X, Y, Z, … Следовательно, в частности

f(X, B, C, …) ≤ f(A, B, C, …)

f(X, Y, C, …) ≤ f(A, B, C, …)

и т. д.; X, Y, Z, … могут быть переменными числами, длинами, углами, точками, …

24. Или x₁ = y₁ = z₁ (исключительный случай), или для n ≥ 1 из трех значений x_n, y_n, z_n только два различны. Обозначим через d_n абсолютную величину разности этих двух значений; например,

d₁ = |x₁ — z₁|, d₂ = |x₂ — z₂|.

По определению

или d₂ = d₁/2. Таким же образом

d_n = d_n—1/2 = d_n—2/4 = … = d₁/2^{n — 1}

и, значит,

25. Рассмотрим n положительных чисел x₁, x₂, …, x_n с данным средним арифметическим A,

x₁ + x₂ + … x_n = nA.

Если не все x₁, x₂, …, x_n равны между собой, то одно из них, скажем x₁, является наименьшим, а другое, скажем, x₂, — наибольшим. (Выбор индексов является безвредным упрощением, только делом удобства обозначений. Мы не сделали неоправданного допущения, что наименьшее значение принимает только x₁.) Тогда

x₁ < A < x₂.

Положим теперь

x′₁ = A, x′₂ = x₁ + x₂ — A, x′₃ = x₃, … x′_n = x_n.

Тогда

x₁ + x₂ + … + x_n = x′₁ + x′₂ + … + x′_n

и

x′₁x′₂ — x₁x₂ = Ax₁ + Ax₂ — A² — x₁x₂ = (A — x₁)(x₂ — A) > 0.

426

Следовательно,

x₁x₂x₃… x_n < x′₁x′₂x′₃… x′_n.

Если не все x′₁, x′₂, …, x′_n равны между собой, то мы повторяем этот процесс, получая другое множество из n чисел x″₁, x″₂, …, x″_n, таких, что

x′₁ + x′₂ + … + x′_n = x″₁ + x″₂ + … + x″_n.

x′₁x′₂x′₃… x′_n < x″₁x″₂x″₃… x″_n.

Множество x′₁, x′₂, …, x′_n имеет по крайней мере один элемент, равный A, множество x″₁, x″₂, …, x″_n имеет по крайней мере два элемента, равных A. В самом последнем множестве, x₁^{(n — 1)}, x₂^{(n — 1)}, … x_n^{(n — 1)} будет содержаться n — 1 и, следовательно, n элементов, равных A, и, таким образом,

26. Соединяя общую начальную точку перпендикуляров x, y, z с тремя вершинами треугольника, мы подразделяем последний на три меньших треугольника. Выражая тот факт, что сумма площадей этих стрех частей равна площади целого, мы получаем x + y + z = l. Уравнение x = const изображается прямой, параллельной основанию нашего равностороннего треугольника, уравнение y = z — высотой. Первый отрезок ломаной линии на рис. 8.9 параллелен основанию и оканчивается на высоте. Первый шаг примера 25 изображается отрезком, параллельным основанию и оканчивающимся на прямой с уравнением y = l/3, параллельной другой стороне и проходящей через центр. Второй шаг изображается отрезком на линии y = l/3, оканчивающимся в центре.

27. Для решения, основанного на модели примера 25, см. Радемахер — Теплиц, стр. 21—25, 158—163.

28. Частное изменение.

29. В точке, где достигается экстремум, при подходящем значении λ выполняются равенства

Это условие выводится при допущении, что одновременно не обращаются в нуль обе частные производные . При дополнительном допущении, что не обращаются в нуль одновременно обе частные производные эти равенства, содержащие λ, выражают, что кривая g = 0 (предписанный путь) касается в точке экстремума кривой f = const (линии уровня), проходящей через эту точку.

30. В вершине или в перевале В угловой точке предписанного пути (если они существуют) обе = 0. Экстремум в начальной (или концевой) точке предписанного пути вообще не подпадает под аналитическое условие, приведенное в примере 29, которое относится к экстремуму по отношению ко всем точкам (x, y) в некоторой окрестности, удовлетворяющим условию g (x, y) = 0.

31. Вот условие

Допускается, что не все три частные производные функции g равны нулю. При дополнительном допущении, что не все три частные производные функции f

427

равны нулю, эти три равенства выражают, что поверхность g = 0 и поверхность f = const, проходящие через точку экстремума, касаются одна другой в этой точке.

32. Условие состоит из трех равенств, из которых первое, относящееся к оси x, таково:

Допускается, что не все три определителя, из которых первым является

равны нулю. При дополнительном допущении, что не все три частные производные функции f равны нулю, эти три равенства выражают, что кривая, являющаяся линией пересечения двух поверхностей g = 0 и h = 0, касается поверхности f = const, проходящей через точку экстремума, в этой точке.

34. Вот желаемое заключение: только для куба достигается минимум. Следовательно, когда неравенство, которое нам нужно доказать, становится равенством, должен появиться куб, т. е. мы должны иметь x = y, или (если говорить о площадях) x² = xy. Однако неравенство, которым мы (без успеха) воспользовались, превращается в равенство, когда 2x² = 4xy: мы могли бы поэтому предсказать, что оно ничего нам не даст.

Заглядывая или не заглядывая в § 6, мы делим S на три пары противоположных граней:

S = 2x² +2xy +2xy

и применяем теорему о средних:

(S/3)³ ≥ 2x²·2xy·2xy = 8x⁴·y² = 8V².

Равенство достигается в том и только в том случае, если 2x² = 2xy или x = y, т. е. только для куба.

Выведите мораль: предвидение того, в каком случае достигается равенство, может руководить нашим выбором, может дать указание.

35. Пусть V, S, x и y обозначают, соответственно, объем, площадь поверхности, радиус и высоту цилиндра, так что

V = πx²y, S = 2πx² + 2πxy.

Желаемое заключение, y = 2x, руководит нашим выбором: при

S = 2πx² + πxy + πxy

теорема о средних дает

(S/3)³ ≥ 2πx²·πxy·πxy = 2π³x⁴y² =2πV²,

причем равенство имеет место только для y = 2x.

36. Пример 34 является частным случаем, а пример 35 — предельным случаем. Пусть V, S, y и x соответственно обозначают объем, площадь поверхности, высоту призмы и длину какой-либо стороны ее основания. Пусть a и l соответственно обозначают площадь и периметр многоугольника, подобного основанию, у которого сторона, соответствующая стороне основания длины x, имеет длину 1. Тогда

V = ax²y, S = 2ax² + lxy.

В примерах 34 и 35 минимум S достигался, когда площадь основания (теперь ax²) была равна S/6. Ожидая, что это будет выполняться и в настоящем общем случае, мы имеет указание; положим

S = 2ax² + lxy/2 + lxy/2.

и получим, пользуясь теоремой о средних,

(S/3)³ ≥ 2ax²·(lxy)²/4 = [l²/(2a)]V²,

причем равенство имеет место, если ax² = lxy/4 = S/6.

37. Пусть V, S, y и x соответственно обозначают объем двойной пирамиды, площадь ее поверхности, сторону ее основания и высоту одной из составляющих ее пирамид. Тогда

V = 2x²y/3, S = 8x[(x/2)² + y²]^½/2.

В случае правильного октаэдра двойная высота составляющей пирамиды равна диаметру основания или

2y = 2^½x, или 2у² = x².

Получив это указание, положим

S² = 4x²(x² + 2у² + 2у²)?

(S/3)³ ≥ 4³x⁶x²2у²2у² = 4⁴x⁸у⁴ = (6V)⁴.

Равенство осуществляется, только если x² = 2у². Отметьте, что в этом случае S = 3^½x².

38. Пусть V, S, y и x, соответственно, обозначают объем двойного конуса, площадь его поверхности, радиус его основания и высоту одного из составляющих его конусов. Тогда

V = 2πx²y/3, S = 2·2πx(x² + y²)^½/2.

Рассмотрим прямоугольный треугольник с катетами x, y и гипотенузой (x² + y²)^½. Если проекция x на гипотенузу равна ⅓ последней (как мы надеемся, это будет в случае минимума), то

x² = (x² + y²)/3,

или 2 x² = y². Получив это указание, положим

S² = 2π²x²(2x² + y² + y²),

(S²/3) ≥ 8π⁶x⁶·2x²y²y² = π²(3V)⁴.

Равенство осуществляется, только если 2x² = y². Отметьте, что в этом случае S = 3^½2·πx².

39. Пусть V, S, и y, соответственно, обозначают объем двойной пирамиды, площадь его поверхности и высоту одной из составляющих ее пирамид. Пусть x, a и l таким же образом связаны с основанием призмы. Пусть p обозначает радиус круга вписанного в основание. Тогда

V = 2ax²y/3, ax² = lpx/2, S = 2lx (p² + y²)^½/2 = (4a²x⁴ + l²x²y²)^½.

В примерах 37 и 38 S было минимально, когда S = 3^½/2ax², что дает

l²x²y² = 8a²x⁴.

Замечая это указание, положим

S² = 4a²x⁴ + l²x²y²/2 + l²x²y²/2,

(S²/3)³ ≥ 4a²x⁴·(l²x²y²)²/4 = (l⁴/a²)(3V/2)⁴.

Равенство осуществляется в том и только в том случае, если площадь основания ax² = S/(3^½2).

40. Есть правдоподобное предположение: наименьший периметр при данной площади или наибольшую площадь при данном периметре имеет равносторонний треугольник. Пусть a, b, c, A и L = 2p соответственно обозначают три стороны треугольника, его площадь и периметр. По формуле Герона

A² = p(p — a) (p — b) (p — c).

Очень напрашивается применение теоремы о средних: когда p дано, A не должно быть слишком велико; правая часть есть произведение. Но как нам следовало бы применить эту теорему? Вот указание: если треугольник равносторонний, то a = b = c, или p — a = p — b = p — c. Поэтому мы поступаем следующим образом:

То есть A² ≤ L⁴/(2⁴3³), и равенство имеет место только в случае равностороннего треугольника. Ср. пример 16.

41. Имеется правдоподобное предположение: квадрат. Пусть a и b заключают угол φ, c и d — угол ψ, и φ + ψ = ε. Получаем

2A = ab sin φ + cd cos ψ.

Выражая диагональ четырехугольника, отделяющую φ от ψ, получаем

a² + b² — 2ab cos φ² = c² + d² — 2cd cos ψ.

Из трех соотношений мы можем теперь исключить φ и ψ. Складывая

(a^2 + b^2 — c^2 — d^2)^2 =	4a^2b^2 cos^2 φ + 4c^2d^2 cos^2 ψ — 8abcd cos φ cos ψ,
16A^2 =	4a^2b^2 sin^2φ + 4c^2d^2 sin^2ψ + 8abcd sin φ sin ψ,

получаем

16A² + (a² + b² — c² — d²)² = 4a²b² + 4c²d²— 8abcd cos ε = 4(ab + cd)² — 16abcd (cos ε/2)².

Наконец, замечая разности квадратов и полагая

a + b + c + d = 2p = L,

находим

A² = (p — a) (p — b) (p — c) (p — d) — abcd (cos ε/2)².

В вероятном случае равенства (квадрат) стороны равны и, следовательно, равны величины p — a, p — b, p — c, p — d. Пользуясь этим указанием, получаем

Чтобы оба встретившиеся неравенства стали равенствами, мы должны иметь ε = 180° и a = b = c = d.

42. Призма более доступна, чем два других тела, за которые мы возьмемся, после тщательной подготовки, в примерах 46 и 47. Пусть L обозначает периметр основания, а h — высоту призмы. Любая боковая грань является параллелограммом; его основанием служит одна из сторон основания призмы, а его высота ≥ Lh, и равенство достигается в том и только в том случае, если все боковые грани перпендикулярны основанию и, таким образом, призма является прямой призмой.

43. Пусть x_j, y_j — координаты точки P_f для j = 0, 1, 2, …, n, и положим

x_j = x_j—1 + u_j, y_j = y_j—1 + v_j

430

для j = 1, 2, …, n. Тогда левая часть неравенства, которое требуется доказать, равна длине ломаной P₀P₁P₂ … P_n, а правая часть — длине прямолинейного отрезка P₀P_n, являющегося кратчайшим расстоянием между концами ломаной.

44. В случае n = 2 мы исследуем (обозначения слегка изменены) утверждение

(u² + v²)^½ + (U² + V²)^½ ≥ [(u + U)² + (v + V)²]^½.

С помощью возведения в квадрат и других алгебраических операций преобразуем его в эквивалентные формы:

(u² + v²)^½(U² + V²)^½ ≥ uU + vV, u²U² + v²V² ≥ 2uvUV, (uV — vU)² ≥ 0.

В своей последней форме утверждение, очевидно, верно. Равенство достигается в том и только в том случае, если

u : v = U : V.

В случае n = 3 мы приходим к результату, дважды применяя случай n = 2:

(u₁² + v₁²)^½

И так далее, для n = 4, 5, … В действительности нужно воспользоваться математической индукцией.

45. Пусть h — высота и пусть основание разбивается точкой пересечения с высотой на два отрезка соответственно длины p и q. Мы должны доказать, что

это случай примера 43. Для равенства мы должны иметь

p : h = q : h,

или p = q, т. е. равнобедренный треугольник.

46. Пусть h — высота пирамиды P, a₁, a₂, …, a_n — стороны ее основания и p₁, p₂, …, p_n — перпендикуляры, опущенные из точки пересечения высоты с основанием на соответствующие стороны. Пусть Σ обозначает суммирование по j, причем j изменяется от j = 1 до j = n. Тогда

A = Σ a_jp_j/2,

S = A + Σa_j(p_j² + h²)^½/2.

Эти выражения для прямой пирамиды P₀ становятся проще, так как в этом случае все перпендикуляры, опущенные из точки пересечения высоты с основанием на стороны, имеют общее значение p₀. Следовательно,

A₀ = L₀p₀/2,

S₀ = A₀ + L₀(p₀² + h₀²)^½/2 = A₀ + (A₀² + h²L₀²)^½/2;

P и P₀ имеют одну и ту же высоту 3V/A = 3V₀/A₀ = h. Пользуясь примером 43 и нашими допущениями, получаем

2(S — A) = Σ[(a_jp_j)² + (a_jh)²]^½ ≥ [(Σa_jp_j)² + (Σa_jh)²]^1/2 = [4A² + h²L²]^½ ≥ [4A² + h²L²]^½ =2(S₀ — A).

431

Следовательно, S ≥ S₀. Для равенства должны стать равенствами оба встретившихся неравенства и, таким образом, должны удовлетворяться два условия. Во-первых,

p₁ : h = p₂ : h = … = p_n : h,

т. е. P — прямая пирамида. Во-вторых, L = L₀.

47. Сделаем два шага: (1) Заменим основание двойной пирамиды D основанием двойной пирамиды D₀ и обе пирамиды, из которых состоит D, — прямыми пирамидами, оставив, однако, неизменными их высоты. Мы получим таким образом двойную пирамиду D′, которая не обязательно является прямой двойной пирамидой. (Составляющие ее две пирамиды являются прямыми пирамидами, но, возможно, разной высоты.) (2) Заменим D′ на D₀. Шаг (1) в силу примера 46 может только уменьшить поверхность. Высоты двух пирамид, составляющих D′, имеющие длины h₁ и h₂, лежат на одной и той же прямой. Пусть p₀ обозначает радиус круга, вписанного в основание двойной пирамиды D₀. Тогда площадь поверхности D′ равна

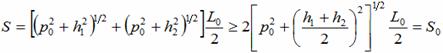
в силу примера 45.

48. Оставляя все время неизменным объем V, сделаем три шага: (1) Оставляя основание неизменным по форме и по размерам, преобразуем нашу призму в прямую призму. (2) Оставляя неизменной площадь основания A, преобразуем основание в квадрат. (3) Преобразуем прямую призму с квадратным основанием в куб. шаги (1) и (3), соответственно, в силу примеров 42 и 34, могут только уменьшить поверхность S. Шаг (2) оставляет неизменной высоту h = V/A и может в силу примера 41 только уменьшить L, периметр основания; но S = 2A + Lh. Если призма с самого начала не является кубом, то по крайней мере один из этих трех шагов действительно уменьшит S. Точкой опоры служит более слабая теорема 34.

49. Это следует из примеров 47, 41 и 37, как предыдущий пример 48 следует из примеров 42, 41 и 34. Однако благодаря точной формулировке примера 47 мы можем с выгодой объединить два шага, соответствующих шагам (1) и (2) примера 48, в один шаг.

50. Мы начинаем с произвольной пирамиды с треугольным основанием произвольного тетраэдра, не обязательно правильного). Преобразуем ее в прямую пирамиду, оставляя неизменными объем V и площадь основания A, но изменяя (если это необходимо) основание в равносторонний треугольник. Это силу примера 40 уменьшает периметр основания L и, следовательно, в силу примера 46 площадь поверхности S. Боковые грани новой пирамиды являются равнобедренными треугольниками. Если они не будут равносторонними треугольниками. Если они не будут равносторонними треугольниками, то возьмем в качестве основания один из них и повторим процесс, снова уменьшая S. в силу принципа частного изменения (пример 22), если вообще существует тетраэдр с данным объемом V и наименьшей S, то он должен быть правильным тетраэдром.

51. См. пример 53.

52. См. пример 53.

53. Пусть V, S и y обозначают объем, площадь поверхности и высоту пирамиды и пусть x, a и l связаны с основанием пирамиды таким же образом, как в решении примера 36 они связаны с основанием призмы. Пусть p обозначает радиус круга, вписанного в основание. Тогда

V = a x²у/3, ax² = lxp/2,

S = ax² + lx(p² + y²)^½/2 = ax² + (4a²x⁴ + l²x²y²)^½/2.

Пытаясь ввести выражение, зависящее от формы, но не от размеров основания, мы приходим к рассмотрению отношения

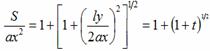
(мы ввели сокращение, положив [ly/(2ax)]² = t) и

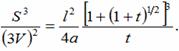
Поскольку V дано, а S должно быть минимальным, левая часть должна быть минимальной. Следовательно, минимальной должна быть и правая часть. Однако форма дана, и, таким образом, l²/2 дано. Поэтому все, что нам остается сделать, это найти значение t, делающее правую часть минимальной: это значение не зависит от формы. Оно одинаково пригодно для всех частных форм, например, форм, упомянутых в примерах 51 и 52. Однако есть частная форма, для которой мы знаем результат: если основание есть равносторонний треугольник, то в силу примера 50 наилучшее отношение S : ax² площади полной поверхности к площади основания равно 4 : 1. Так как S/(ax²) зависит только от t, это остается справедливым и для всех форм и дает

1 + (1 + t)^½ = 4, t = 8.

54. Читателю следует скопировать следующую таблицу, подставляя вместо номара задачи соответствующую фигуру.

	(1)	(2)	(3)	(4)	(5)	(6)	(7)
(a)	34	35	36	42	u	45	x
(b)	51	52	53	46	50	v	y
(c)	37	38	39	47	w	49	z
(d)	—	—	—	—	40	41	n

Строки: (a) призмы, (b) пирамиды, (c) двойные пирамиды, (d) многоугольники (о которых речь может идти только в случае трех последних столбцов).

Столбцы: (1) прямая с квадратным основанием, (2) прямая с кругом в качестве основания (3) прямая с основанием данной формы, (4) переход от наклонной к прямой, (5) произвольное треугольное основание, (6) произвольное четырехугольное основание (7), произвольное многоугольное основание с данным числом n сторон.

Аналогия может подсказать теоремы, которые, как можно ожидать, заполнят пропуски, помеченные буквами u, v, w, x, y, z и n. Вот некоторые из них:

(u) Призма, имеющая наименьшую поверхность из всех трехгранных призм данного объема, обладает следующими свойствами: ее основание является равносторонним треугольником, площадь ее основания составляет ¹/₆ полной площади ее поверхности, она описана вокруг шара, который касается каждой грани в центре этой грани.

(y) Пирамида, имеющая наименьшую поверхность из всех пирамид с n-угольником в основании и данном объемом, обладает следующими свойствами: ее основание является правильным многоугольником, площадь ее основания составляет ¹/₄ полной площади ее поверхности, она описана вокруг шара, который касается каждой грани в центре тяжести этой грани.

На основании предыдущего мы легко можем доказать (u), (v) (w), но (x), (y) и (z) зависят от (n), которое мы рассмотрим позднее; см. § 10.7(1).

55. (1) Пользуясь методом и обозначениями § 6, имеем

V = abc, S₅ = ab + 2ac + 2bc, (S₅/3)³ ≥ ab·2ac·2bc = 4V²,

433

причем равенство достигается в том и только в том случае¸ если ab = 2ac = 2bc или a = b = 2c; этот ящик является половиной куба.

(2) Пользуясь результатом § 6, рассмотрим плоскость грани, не причисляемой к S₅, в качестве зеркала. Ящик вместе с его зеркальным отражением образует новый ящик с объемом 2V, у которого задана полная поверхность = 2S₅. В силу § 6 новый (двойной) ящик, когда достигается максимум объема, должен быть кубом.

56. Следуя примеру 55, рассмотрите плоскость недостающей грани в качестве зеркала. Максимум достигается для трехгранной призмы, которая является половиной куба, получающейся при его разбиении диагональной плоскостью. Примените пример 45 с дополнительным замечанием.

57 [Путнэм 1950]. Следуя примерам 55 и 56, рассмотрите плоскости обеих недостающих граней в качестве зеркал. Максимум достигается для трехгранной призмы, являющейся четвертью куба; куб делится на четыре конгруэнтные обломка двумя плоскостями симметрии, одна из которых — диагональная плоскость, а другая перпендикулярна первой и параллельна двум граням.

58. Пусть A, L, r и s обозначают, соответственно, площадь, периметр, радиус и дугу сектора. Тогда

A = rs/2, L = 2r +s, (L/2)² ≥ 2r·s — 4A;

мы пользуемся теоремой о средних. Равенство достигается, когда s = 2r и угол сектора равен двум радианам.

59. Пусть u, v и w обозначают стороны треугольника, A — площадь, γ — данный угол, противоположный w. Тогда

2A = uv sin γ.

(1) [(u + v)/2]² ≥ uv = 2A/ sin γ,

по теореме о средних. Равенство достигается, когда u = v, т. е. когда треугольник равнобедренный.

(2) w² = u² + v² — 2 uv cos γ = u² + v² — 4A ctg γ, (u² + v²)/2 ≥ uv = 2A/sin γ.

Равенство достигается, и, таким образом, w имеет минимум, когда u² = v² и треугольник равнобедренный.

(3) Поскольку и u + v, и w имеет минимум, когда треугольник равнобедренный, то и u + v + w имеет максимум при этом же условии.

60. Воспользуйтесь обозначениями примера 59. Данная точка лежит на стороне w. Проведите из данной точки параллели к u и v, оканчивающиеся на v и u, и обозначьте их, соответственно буквами a и b; a и b даны (фактически они являются косоугольными координатами). Из подобных треугольников

Равенство имеет место в том и только в том случае, если и данная точка является серединой стороны w.

61. Воспользуйтесь обозначениями § 6 и теоремой о средних.

(1) V = abc ≤ [(a + b + c)/3]³ = [E/12]³.

(2) S = 2ab + 2ac +2bc ≤ a² + b² + a² + c² + b² + c² = 2(a + b + c)² — 4(ab + ac +bc), т. е.

3S ≤ 2(E/4)².

В обоих случаях равенство достигается только для a = b = c, т. е для куба.

434

62. Воспользуйтесь обозначениями § 6 и теоремой о средних. Длина равна c, обхват 2 (a + b) и

V = (2a·2b·c)/4 ≤ [(2a + 2b +c)/3]³/4 ≤ l³/108.

Равенство достигается только для 2a = 2b = c = l/3.

63. Воспользуйтесь обозначениями решения примера 35. Тогда

d² = (2x)² + (y/2)² = 2 (x² + x² + y²/8)

и, следовательно, по теореме о средних,

V² = π²x⁴y² = 8π²x²·x²·y²/8 ≤ 8π²(d²/6)³,

причем равенство достигается только если

x² = y²/8 = d²/6.

По поводу исторического фона ср. Toeplitz O., Die Entwicklung der Infinitesimalrechnung, S. 78—79.

Нет решения: 23, 33.

ГЛАВА IX

1. (1) Представьте себе два зеркала, перпендикулярных плоскости чертежа, одно из которых проходит через l, а другое — через m. Человек в P смотрит в m и видит себя со стороны: свет, приходящий из P, возвращается в P после первого отражения в l и второго в m. Свет, выбирая кратчайший путь, описывает искомый ∆ PYZ с наименьшим периметром; стороны ∆ PYZ образуют с l и m равные углы, соответственно, в точках Y и Z. (2) Пусть P′ и P″ — зеркальные изображения точки P, соответственно, относительно l и m. Отрезок прямой, соединяющий P′ и P″, пересекает l и m, соответственно, в искомых точках Y и Z, и его длина равна искомому наименьшему периметру (по идее рис 9.3, примененной дважды).

2. (1) Свет после трех последовательных отражений в трех круглых зеркалах возвращается к своему источнику по противоположному направлению. (2) Замкнутая резиновая лента связывает три жестких кольца. Обе интерпретации подсказывают, что две стороны искомого треугольника, выходящие из вершины, лежащей на данной окружности, образуют ровные углы с радиусом.

3. Путь света с возвращением в исходную точку или замкнутая резиновая лента, как в примере 2. XY и XZ одинаково наклонены к BC и т. д.

4. n-угольник минимального периметра, вписанный в данный n-угольник, обладает следующим свойством: две стороны минимального n-угольника, общая вершина которых лежит на стороне s данного n-угольника, одинаково наклонены к s. См., однако, примеры 6 и 13.

5. Обозначьте буквой A точку пересечения прямых l и m. Возьмите точку B на m и точку C на l так, чтобы ∠ BAC (меньший 180°) содержал внутри себя точку P. Тогда, по закону отражения,

∠ P″AB = ∠ BAP, ∠ PAC = ∠ CAP′,

и поэтому

∠ P″AP′ = 2 ∠ BAC.

Решение теряет силу, когда ∠ P″AP′ ≥ 180°, или, что то же самое, когда данный ∠ BAC ≥ 90°.

6. Решение нельзя применить, когда данный треугольник имеет угол ≥ 90°, см. пример 5. решение примера 4, конечно, и подавно[276] имеет исключения.

7. Фиксируйте на время X в положении P на стороне BC. Тогда применимо решение (2) примера 1 (так как ∠ BAC острый; см. пример 5); минимальный периметр равен PP″. Теперь длина PP″ зависит отP; остается найти минимум P′P″. (Поскольку сам отрезок P′P″ был получен как минимум, мы разыскиваем минимум этих минимумов, или «minimum minimorum».) По закону отражения, P″A = PA = P′A. Следовательно ∆ P″AP′ является равнобедренным, его угол в A

435

не зависит от P (см. пример 5) и, таким образом, его форма не зависит от P. Поэтому P′P″ становится минимальным, когда минимальным становится P′A = PA, а это, очевидно, имеет место, когда PA ⊥ BC; ср. § 8.3. Вершины треугольника с минимальным периметром, вписанного в данный остроугольный треугольник, являются основаниями трех высот данного треугольника. Сравнивая это с решением примера 3, мы видим, что _высоты остроугольного треугольника делят пополам соответствующие углы вписанного треугольника, вершинами которого являются основания высот. Последний результат, конечно, совершенно элементарен. Приведенное здесь решение принадлежит Л. Фейеру. Ср. Курант—Роббинс, стр. 454—459.

8. Нет. Если ∆ ABC имеет угол ≥ 120°, то транспортным центром является вершина этого угла. На это сильно наталкивает механическое решение в § 2 (2).

9. [Путнэм 1949]. Эта задача находится в тесной аналогии с более простой плоской задачей, рассмотренной в § 1 (4), § 2 (2) и в примере 8. Какой метод следовало бы нам избрать? (1) Механическая интерпретация по образцу рис. 9.7. Имеется четыре блока, по одному в каждой из четырех данных точек A, B, C и D. Четыре нити соединены в точке X; каждая нить проходит через один из блоков, и к ней в другом ее конце подвешен груз в один килограмм. Как в § 2 (2), первое рассмотрение (потенциальной энергии) показывает, что предложенной задаче на минимум соответствует положение равновесия этой механической системы. Второе рассмотрение относится к силам, действующим на точку X. Имеется четыре таких силы; они равны по величине и идут в направлении четырех туго натянутых нитей, соответственно, к A, B, C и D. Равнодействующая двух первых сил должна уравновешивать равнодействующую двух последних сил. Следовательно, эти равнодействующие идут по одной и той же прямой, которая делит пополам и ∠AXB, и ∠CXD. Из конгруэнтности двух параллелограммов сил (оба они — ромбы) следует равенство этих углов. Подобным же образом связны пары ∠AXC и ∠BXD, ∠AXD и ∠BXC. (2) Частное изменение и оптическая интерпретация, по образцу рис. 9.4. Сохраните (на время) постоянной сумму двух расстояний, CX + DX. Тогда точка X должна находиться на поверхности вытянутого сфероида (эллипсоида вращения) с фокусами в C и D. Мы представляем себе эту поверхность как зеркало. Свет, исходящий из A, отражается в нашем сфероидальном зеркале и, приходя в B, делает сумму AX + XB минимальной; на его пути ∠AXB делится пополам нормалью к зеркалу в точке X. Та же самая нормаль в силу § 1 (3) или § 2 (1) делит пополам ∠CXD. Однако с помощью этого метода равенство∠AXB, и ∠CXD получается не так легко: хотя оба эти метода одинаково хорошо работают в более простом аналогичном случае, они не одинаково успешно применяются к настоящей теореме.

10. Да. Где бы ни находилась точка X,

AX + XC ≥ AC, BX + XD ≥ BD,

так как прямолинейный путь между двумя точками является кратчайшим, и оба неравенства становятся равенствами в том и только в том случае, если X является точкой пересечения диагоналей AC и BD: это и есть транспортный центр. Утверждение примера 9 остается вполне правильным ввиду того факта, что нормаль к плоскости четырехугольника является общей биссектрисой ∠AXC и ∠BXD, каждый из которых является углом в 180°.

11. С помощью частного изменения следует из результата § 1 (4). Ср. Курант— Роббинс, стр. 463—471.

13. Ударьте шар параллельно диагонали стола. Рис. 9.14 последовательно применяет четыре раза пример 12. Представьте себе рис. 9.14 начерченным на прозрачной бумаге и согните его по отражающим прямым; тогда отдельные части прямолинейного отрезка PP как раз покроют ромбический путь бильярдного шара. Между прочим, мы видим здесь случай, когда пример 4 имеет бесконечное множество решений.

14. На основании рис. 9.15 (который следует вычертить на прозрачной бумаге)

n2α < 180° < (n + 1)2α, 90°/(n + 1) < α < 90°/n.

436

Начертите фигуры, иллюстрирующие случаи n = 1, 2, 3. Рассмотрите случай n = ∞.

15. Частный случай рассмотрен в § 1, 2, 3, а пример 12 дает некоторые наводящие соображения; см. примеры 16, 17 и 18.

16. Если даны A, B и AX + XB, то геометрическое место точек X есть поверхность вытянутого сфероида (эллипсоида вращения) с фокусами A и B; такие сфероиды являются поверхностями уровня. Решение дает сфероид, для которого данная прямая l является касательной в точке X. Нормаль к этому сфероиду в точке X перпендикулярна к l и делит пополам ∠AXB в силу свойства эллипса, доказанного в § 1 (3) и § 2 (1).

17. Поместите лист бумаги, согнутый пополам, так. Чтобы линия сгиба совпала с l и чтобы одна половина листа (полуплоскость) проходила через A, а другая — через B. Искомая кратчайшая линия, конечно, описывается на этом согнутом листе. Если лист развернуть, то кратчайшая линия становится прямой. На согнутом, как и на развернутом листе прямые XA и XB образуют с прямой l один и тот же угол.

18. Прикрепите один конец резиновой ленты подходящей длины к A, накиньте эту ленту на жесткий стержень l в точкеX и прикрепите другой конец к B так, чтобы лента натянулась: она образует таким образом кратчайшую линию, требуемую примером 15 (если пренебречь трением). На точку X действуют три силы: два натяжения, равные по величине, одно из которых направлено к A, а другое — к B, и реакция стержня, направленная перпендикулярно l (так как мы пренебрегаем трением). Параллелограмм сил есть ромб, и, таким образом, нормаль к l делит ∠AXB пополам, как мы и нашли в примере 16. Реакция стержня не имеет составляющей, параллельной стержню, и поэтому составляющие натяжений, параллельные стержню, должны быть равны по величине ( и противоположны по направлению). Следовательно XA и XB одинаково наклонены к l, как мы и нашли в примере 17. Между прочим, эквивалентность результатов примеров 16 и 17 можно показать с помощью небольших сведений из пространственной геометрии. (Трехгранные углы равны, если у них одинаковы три подходящих элемента.)

19. Замкнутая резиновая лента, надетая на три жестко закрепленных вязальных спицы. Частное изменение и пример 16 или пример 18; биссектрисы трех углов треугольника пересекаются в центре вписанной окружности. Пример 3 является предельным случаем.

20. Каждая вершина треугольника является серединой ребра куба. Треугольник равносторонний; его центр является центром куба; его периметр равен 3√̅6̅ a.

21. В силу принципа частного изменения § 8.3 и § 1 (4) или 2 (2), TX, TY и TZ перпендикулярны соответственно a, b и c и одинаково наклонены один к другому (120°). Мы могли бы назвать T «транспортным центром трех скрещивающихся прямых». Задача § 1 (4) является крайним случаем этой задачи: a, b и c становятся параллельными. Существует очевидное обобщение и несколько аналогичных задач: транспортный центр трех сфер, транспортный центр точки, прямой и плоскости и т. д.

22. Транспортным центром трех скрещивающихся ребер куба, конечно, является центр куба. Ясно представьте себе поворот куба на 120° переставляющий три данных скрещивающихся ребра, и положение треугольника, найденного в примере 20.

23. Чтобы найти кратчайшую линию, соединяющую две данные точки A и B на поверхности многогранника, представьте себе многогранную поверхность, сделанную из картона, из плоских многоугольников, скрепленных петлями и подходящим образом согнутых. Разверните эту многогранную поверхность на плоскость (разложите картон ровно на письменном столе): искомая кратчайшая линия станет прямой, соединяющей A и B. Прежде чем разворачивать многогранную поверхность, мы должны разрезать ее по подходящим ребрам, которые кратчайшая линия не пересекает. Поскольку мы заранее не знаем, какие грани и какие ребра будет пересекать кратчайшая линия, мы должны исследовать все допустимые комбинации. Обратимся теперь к предложенной задаче, запишем существен-

437

ные последовательности граней и отметим для каждой последовательности квадрат прямолинейного расстояния от паука до мухи по этой последовательности.

(1) Передняя стена, потолок, задняя стена:

(0,5 + 10 + 3,5)² = 196.

(2) Передняя стена, потолок, боковая стена, задняя стена:

(0,5 + 10 + 2)² + (2 + 3,5)² = 186,5.

(3) Передняя стена, потолок, боковая стена, пол, задняя стена:

(0,5 + 10 + 0,5)² + (2 + 4 + 2)² = 185.

24. На сфере геодезической линией является дуга большого круга. Большой круг есть плоская кривая; плоскость, в которой лежит большой круг, является центр сферы и поэтому содержит все нормали к сфере (все радиусы), проходящие через точки большого круга. «Малые» круги не являются геодезическими линиями; действительно, плоскость «малого» круга не содержит ни одной нормали к сфере, проходящей через точки «малого» круга.

25. В силу закона сохранения энергии величина скорости точки постоянна, хотя, конечно, направление скорости изменяется. Различие векторов скорости о двух концах короткой дуги траектории точки вызывается нормальной реакцией поверхности, и поэтому разность этих векторов почти нормальна к поверхности. Это — характеристическое свойство геодезической линии; см. пример 24 (2). Другой вариант того же рассуждения: интерпретируем натяжения вдоль резиновой ленты примера 24 (2) иначе, как скорости вдоль траектории; все векторы имеют одну и ту же величину и изменение направления в обоих случаях вызывается нормальной реакцией.

26. Прижмите осторожно n свободных ребер к плоскости (к вашему письменному столу), образовав пирамиду с n равнобедренными боковыми гранями, основание которой есть искомый многоугольник. В самом деле, основание вписано в круг, центр которого является точкой пересечения основания с высотой пирамиды. Радиус круга является катетом прямоугольного треугольника, гипотенуза которого — радиус большого круга, описанного на картоне, а второй катет — высота пирамиды.

27. Если центр тяжести находится настолько близко к полу, насколько это возможно, то имеет место равновесие. Таких простых механических соображений достаточно, чтобы подсказать желаемое решение: возьмите на поверхности многогранника P точку D, для которой расстояние CD минимально. Простое рассмотрение показывает, что D не может быть ни вершиной P, ни лежать на ребре P и что CD перпендикулярен к грани F многогранника P, на которой лежит D. См. Полиа—Сеге, Задачи и теоремы из анализа, т. II, стр. 167, задача 1.

28 (a) Вообразите, что поверхность земли полностью высохла, так что обнажились все вершины, перевалы и котловины. Теперь зальем водой только одну котловину, остальная часть поверхности земли имеет В вершин, П перевалов и К — 1 котловин и может рассматриваться как остров. В силу результата, доказанного в тексте,

В + (К — 1) = П + 1.

(b) Линии уровня и линии наиболее крутого спуска разбивают поверхность земли на Г «стран»; это терминология из примера 3.2. Возьмите столько линий, чтобы каждая замечательная точка, вершина, котловина или перевал, стала вершиной разбиения, как на рис. 9.16 и 9.17, и чтобы ни одна страна не имела на своей границе более одной замечательной точки.

«Распределим» каждое ребро, или граничную линию поровну между двумя странами, которые она отделяет, дав каждой стране по ½ этого ребра. Подобным же образом распределим каждую вершину разбиения. Взамен каждая страна

438

сделает взнос в левую часть формулы Эйлера

В_р — Р + Г[277] = 2[164]

она внесет одну единицу в Г и соответствующую долю в В_р и в — Р. Вычислим этот взнос для различных типов стран.

I. Если на границе страны нет никаких замечательных точек, то эта страна — четырехугольник, содержащийся между двумя линиями уровня и двумя линиями наиболее крутого спуска. Ее взнос в В_р — Р + Г равен

II. Если на границе страны есть вершина или котловина, то эта страна — треугольник; см. рис. 9.16. Если какая-нибудь из этих точек является общей вершиной n стран, то взнос каждой из этих стран в В_р — Р + Г равен

и совместный взнос всех n стран равен n·1/n = 1.

III. Если на границе страны есть перевал, то эта страна — четырехугольник; см. рис. 9.17. Ее взнос в В_р — Р + Г равен

и совместный взнос всех восьми стран, имеющих этот перевал общей вершиной, равен 8·(—1/8) = —1.

Общая сумма всех взносов по формуле Эйлера равна

В + К — П = 2.

(c) Доказательство, использующее идею «потопа», собственно, не является примером «физической математики»: оно пользуется идеями, связанными с повседневным опытом, а не с какой-нибудь специфической физической теорией. Намек в вопросе (b) нашего примера вводил в заблуждение: он, по-видимому, наталкивал на мысль, что В, К и П в каком-то смысле аналогичны Г, В_р и Р, что ни в коем случае не имеет места. Тем не менее это был полезный намек: он направил наше внимание на теорему Эйлера. Это, однако, вполне естественно: идеи, руководящие нами при решении задач, часто бывают совершенно ошибочными и тем не менее полезными.

29. (a) Пусть t₁ — время падения камня, а t₂ — время, за которое звук доходит до вас. Тогда t = t₁ + t₂, d = gt₁²/2, d = ct₂. Исключая t₁ и t₂, и решая квадратное уравнение, находим:

d^½ = — c(2g)^{— ½} ± [c²(2g) ^—1 + ct]^½.

Так как t = 0 должно давать d = 0, то мы должны выбрать знак +. Тогда

d = c²g^—1 + ct — c²g^—1[1 + 2gc^—1t]^½.

(b) d = gt²/2 — g²t³/(2c + …

Пренебрегая членами,здесь не выписанными, мы можем воспользоваться сохраненными двумя членами как подходящей приближенной формулой.

(c) Типично, что на основании физических рассмотрений мы можем предвидеть главный член разложения и даже знак поправки. Типична также математическая процедура, которой мы воспользовались, чтобы получить подходящую приближенную формулу: мы разложили (выражение для d) по степеням малой величины (времени t). Ср. § 5.2.

439

30. Эллиптическое зеркало становится параболическим зеркалом, которое собирает в фокусе все лучи света, падающие на него параллельно его оси. Такое параболическое зеркало является наиболее существенной частью телескопа-рефлектора.

31. Переменные в уравнении разделяются. Мы получаем с помощью очевидных преобразований

Положим, вводя вспомогательную переменную φ,

и получим

y = a (t — sin t), y = a (1 — cos t).

Эта циклоида проходит через точку A, являющуюся началом координат. Существует только одно значение a, при котором первая ветвь циклоиды (соответствующая 0 < t < 2π) проходит через данную точку B. Чтобы это увидеть, будем изменять a от 0 до ∞; при этом циклоида будет «раздуваться», выметая квадрант плоскости, и когда раздуется до правильного размера, пройдет через B.

33. Пусть a — радиус шара (как в § 5), h — высота сегмента, V — его объем и C — объем конуса с тем же основанием, что и сегмент, и с той же высотой h. Начало координат (точка O на рис. 9.13) является общей вершиной сегмента и конуса. Из элементарной геометрии и уравнения окружности, приведенного в § 5,

Воспользуйтесь рис 9.13, но рассмотрите теперь только поперечные сечения, находящиеся от O на расстоянии x, где 0 < x < h. Переходя от равновесия поперечных сечений, выраженного уравнением (A), к равновесию тел (сегмента, конуса — но не нашего конуса объема C — и цилиндра), находим

2a(V + πh²·h/3) = (h/2)π(2a)²h. (B)

Отсюда

2a — h — высота дополнительного сегмента.

34. Запишите уравнение окружности, рассмотренной в § 5, в виде

2aπx² = xπy² + xπx². (A)

Теперь только для πx² поперечное сечение конуса, подвешено в точке H рис. 9.13; поперечное сечение πy² шара и поперечное сечение πx² другого конуса (конгруэнтного с первым) остаются в своем первоначальном положении ( с абсциссой x). Рассмотрите 0 < x < a, перейдите к равновесию трех тел, введите ͞x — абсциссу центра тяжести полушария и вспомните положение центра тяжести конуса (его расстояние от вершины равно ¾ высоты):

2a·πa²·a/3 = ͞x·2πa³/3 + (3a/4) πa²·a/3, ͞x = 5a/8. (Β)

440

35. Сохраните обозначения примера 33, но измените обозначения примера 34 в одном отношении: ͞x теперь обозначает абсциссу центра тяжести сегмента высоты h. Рассмотрите 0 < x < h, перейдите от (A) примера 34 к формуле

2p·πh²·h/3 = ͞xV + (3h/4) πh²·h/3, (B)

что, принимая во внимание значение V, найденное в примере 33 даст

36. Пусть h обозначает высоту, а V — объем сегмента. Напишите обычное уравнение параболы в виде

͞x πy² = x·π (2p)². (A)

Заметьте, поперечное сечение πy² параболоида и поперечное сечение π(2p)² цилиндра. Рассматривая 0 < x < h и переходя от поперечных сечений к телам, находим

2p·V = (h/2) π (2p)²h, (B)

V = πph² = (3/2) π2ph (h/3).

Учтите, что в силу уравнения параболы π2ph есть основание сегмента.

37. Сохраните обозначения примера 36 и пусть ͞x обозначает абсциссу центра тяжести сегмента теперь запишите уравнение параболы в виде

x·πy² = 2p·πx². (A)

Заметьте, πx², поперечное сечение конуса. Рассматривая 0 < x < h и переходя от поперечных сечений к телам, находим ͞xV = 2p·πh² (h/3), а отсюда в силу примера 36

͞x = 2h/3.

38. n = 0: объем призмы, площадь параллелограмма; n = 1: площадь треугольника, центр тяжести параллелограмма или призмы; n = 2: объем конуса или пирамиды, центр тяжести треугольника; n = 3: центр тяжести конуса или пирамиды.

Следует заметить, что метод Архимеда, как он здесь, в § 5 и в примерах 33—38 изложен, подошел бы для курса аналитической геометрии и мог бы придать новый интерес этой теме, которая так легко может стать сухой и надоедливой при обычном изложении. Подобным же образом могут быть рассмотрены и использованы те предложения «Метода», которые мы не обсуждали.

Нет решения: 12, 32.

ГЛАВА X

1. Нет. Пробел не слишком серьезен: существование максимума может быть установлено с помощью общей теоремы, приведенной в гл. VIII, примечание на стр. 154.

2. Явная формула, данная в решении примера 8.41, показывает, что A² ≤ (p — a) (p — b) (p — c) (p — d), и равенство достигается в том и только в том случае, если ε = 180°, т. е в случае, когда четырехугольник вписан в круг.

3. Пусть A, B и C — последовательные вершины правильного n-угольника и M — середина стороны BC. Замените ∆AMB равнобедренным треугольником ∆AB′M (у которого AB′ = B′M), имеющим то же основание AM и тот же периметр и, следовательно, бо́льшую площадь; см. пример 8.8.

4. Если мы выразим обе площади через r, радиус круга, и n, число сторон многоугольника, то останется доказать неравенство:

441

Изящнее будет, если заметим, что правильный многоугольник можно описать вокруг круга: искомый результат является частным случаем примера 5.

5. Многоугольник площади A и периметра L описан вокруг круга радиуса r. Тогда, очевидно, πr² < A. Прямые, проведенные из центра окружности к вершинам многоугольника, делят его на треугольники с общей высотой r; поэтому A = Lr/2. Соединяя оба полученных результата, находим

Итак, L²(4π) есть в точности площадь круга, имеющего периметр L.

6. Пусть A — площадь и L — периметр данной фигуры, а r — радиус круга, имеющего тот же периметр, так что L = 2πr. Пусть A_n обозначает площадь, а L_n — периметр многоугольника P_n, который при n → ∞ стремится к нашей фигуре так, что A_n стремится к A и L_n стремится к L. Рассмотрим многоугольник P′_n, подобный P_n и имеющий периметр L; площадь P′_n равна A_n(L/L_n)². Так как P′_n имеет тот же периметр, что и круг радиуса r, то из § 7 (4) мы заключаем, что

A_n(L/L_n)² < πr².

Переходя к пределу, находим

Это оправдывает отверждение I из § 8. Однако текст § 7 (5) может вызывать возражения: мы определенно не доказали, что A < πr², как, по-видимому, утверждает этот текст. Действительно, когда мы переходим к пределу, условие < может перейти в ≤.

7. Оба утверждения эквивалентны неравенству

V обозначает объем, а S — площадь поверхности ящика. В § 8.6 мы доказали это неравенство непосредственно.

8. Равносильность I′, II′, и III′ доказывается тем же методом, как и равносильность I, II, и III в § 8. Однако I′ не равносильно I. Действительно, I′ в явной форме отрицает возможность, остающуюся неисключенной в I и состоящую в том, что фигура не являющаяся кругом, могла бы иметь тот же периметр и ту же площадь, что и круг. Рассуждение § 7 (5), как оно расширено в примере 6, доказывает I, но не доказывает I′: оно доказывает ≤, что достаточно для I, но не доказывает <, что было бы необходимо для I′.

9. Решение предложенной задачи добавило бы к I из § 8 все, что еще необходимо, чтобы получить I′ из примера 8. этого достаточно, чтобы показать ее важность; по поводу других вопросов см. примеры 10—13.

10. Пусть C″ — наименьший треугольник, содержащий C, L″ — его периметр и A″ — его площадь. Тогда, очевидно, L″ < L и A″ > A. Возьмите в качестве C′ треугольник, подобный C″, с периметром L; площадь C′ равна A′ = A″(L/L″)² > A″ > A.

11. Если C — произвольная, но не выпуклая фигура, то мы сначала рассмотрим наименьшую выпуклую фигуру C″, содержащую C, а затем — C′, подобную C″, но имеющую периметр, равный периметру С. все рассуждение примера 10 вплоть до окончательного неравенства можно повторить в этой более общей ситуации.

12. Возьмите на замкнутой кривой K, ограничивающей фигуру C, две различные точки: P и Q. На K должна найтись третья точка R, не лежащая на прямой, проходящей через P и Q, так как K не может целиком содержаться в прямой линии. Рассмотрите окружность, проходящую через P, Q и R. Если эта окружность не совпадает с K, то на K должна найтись четвертая точка S, не лежащая на этой окружности: задача примера 9 равносильна задаче примера 13.

442

13. Если C — выпуклая фигура, то желаемое построение дает пример 11. Если C выпукла, то P, Q, R и S в каком-то порядке являются вершинами выпуклого четырехугольника. Фигура С состоит сз этого четырехугольника и четырех сегментов. Каждый сегмент ограничен стороной четырехугольника и одной из четырех дуг, на которые точки P, Q, R и S делят кривую, ограничивающую C. Следуя идее Штейнера [см. § 5 (2), рис. 10.3 и 10.4], рассмотрим эти четыре сегмента как жесткие (из картона) и жестко прикрепленные к соответствующим сторонам четырех угольника, который мы рассматриваем как суставчатый (с гибкими суставами в четырех вершинах. Примем обозначения примера 8.41. Тогда в силу нашего основного условия ε ≠ 180°. Небольшое движение суставчатого четырехугольника изменяет[278] ε в ε′. Выберем ε′ столь близким к ε, чтобы четыре дуги, жестко прикрепленные к сторонам, все еще образовывали не самопересекающуюся кривую, ограничивающую фигуру C′. Кроме того, мы выбираем ε′ так, чтобы

|ε′ —180°| < |ε —180°|.

Отсюда, в силу формулы для A², данной в решении примера 8.41, следует, что площадь C′ больше, чем площадь C. Однако граница C′ состоит из тех же четырех дуг, что и граница C; C′ и C имеют один и тот же периметр.

14. Оба умозаключения имеют одну и ту же логическую форму. Однако второе умозаключение, ведущее к очевидно ложному результату, должно быть неправильным. Следовательно, должно быть неправильным и первое умозаключение, хотя оно имеет целью результат, который мог бы оказаться истинным. Второе умозаключение в действительности является остроумной пародией на первое, принадлежащей О. Перрону.

Между этими двумя случаями должно быть какое-то другое различие, не упомянутое в предложенном тексте. Не существует наибольшего целого числа. Все же среди всех изопериметрических фигур существует фигура с наибольшей площадью. Этого, однако, мы не узнали из примеров 10—13.

15. Фигура C не является кругом, но имеет тот же периметр, что и некоторый круг. Площадь C в силу примера 6 не может быть больше, чем площадь круга. Я утверждаю, что площадь C не может быть равна площади круга. В противном случае, как мы знаем из примеров 10—13, существовала бы другая фигура, все еще с тем же периметром, что и круг, но с большей площадью, что невозможно в силу утверждения, доказанного в примере 6.

16. Даны две точки, A и B, на рис. 10.13, соединенные прямой и переменной кривой, вместе окружающими область. Рассмотрим длину этой кривой и площадь этой области. В тексте мы рассматривали длину кривой, как данную и разыскивали максимум площади области. Здесь мы рассматриваем площадь как данную и разыскиваем минимум длины. В обоих случаях решение одно и то же: дуга окружности. Даже доказательство, по существу, одинаково. Здесь, как и там, мы можем пользоваться рис. 10.14. Конечно, существует и очевидное различие; (незаштрихованный) сегмент круга на рис 10.14 строится теперь по данной площади, а не по данной длине, и мы пользуемся теперь не теоремой I′ примера 8, а теоремой II′.

17. Воспользуйтесь примером 16: отождествите точки X и Y рис 10.11, соответственно, с точками A и B рис. 10.13 и прибавьте к рис. 10.13 неизменяемый ∆XYC. Максимум достигается, когда линия данной длины является дугой окружности.

18. Рассматривайте на рис 10.11 линию CY как зеркало. Пусть X′ — зеркальное изображение X, и примените к ∠XCX′ и к двум данным точкам X и X′ на двух его сторонах пример 17. Максимум достигается, когда линия данной длины является дугой окружности, перпендикулярной к CY в точке Y.

19. Примените частное изменение. Рассматривайте точку X как фиксированную: решением, в силу примера 18, является дуга окружности, перпендикулярная к CY. Рассматривайте как фиксированную точку Y: дуга окружности перпендикулярна к CX. Окончательно, решением является дуга окружности,

443

перпендикулярная к CX и CY, и, таким образом, как и предполагалось в § 9, ее центр находится в C.

20. Максимум достигается, когда прямолинейный отрезок перпендикулярен к биссектрисе угла. Если бы мы заранее знали, что существует только одно решение, то это следовало бы из симметрии. Этот результат без такого допущения следует из примера 8.59 (2).

21. По идее рис. 10.14 максимум достигается, когда веревки BC и DA являются дугами одной и той же окружности, для которой палки AB и CD являются хордами.

22. Замкнутая линия, состоящая из 2n кусков, n палок вперемежку с n веревками, ограничивает максимальную площадь, когда все палки являются хордами, а все веревки дугами одной и той же окружности.

23. Когда все веревки примера 22 имеют длину 0, мы получаем § 5 (2) и рис. 10.3 и 10.4.

24. Аналог примера 16: жесткий диск, переменная поверхность данной площади и окружность, являющаяся краем и диска¸ и поверхности, соответственно, аналогичны палке, веревке и паре точек A и B. Применим метод примера 16. (На рис. 10.14 вращайте окружность 1. Применим метод примера 16. (На рис. 10.14 вращайте окружность I вокруг ее вертикального диаметра и то же самое проделайте с сегментом в нижней части рис. II, но его верхнюю часть измените более произвольным образом.) Принимая изопериметрическую теорему в пространстве, получаем: ограничиваемый объем максимален, когда поверхность данной площади является порцией (поясом с одним основанием) сферы.

25. Возьмите три взаимно перпендикулярные плоскости и без доказательства примите изопериметрическую теорему в пространстве. Тогда трехгранный угол становится октантом, и вы можете воспользоваться пространственным аналогом рис. 10.12. С помощью последовательных отражений в трех плоскостях поверхность, рассекающая октант, превращается в замкнутую поверхность; ее площадь и ограничиваемый ею объем, соответственно, в восемь раз больше данной площади и объема, отсекаемого первоначальной поверхностью. Замкнутая поверхность данной площади, ограничивающая максимальный объем, является сферой. Следовательно, в нашем частном случае предложенной задачи максимум достигается, когда поверхность данной площади является порцией[279] (1/8) сферы с центром в вершине трехгранного угла.

26. Конфигурация, рассмотренная в решении примера 25, является частным случаем n = 2 следующей общей ситуации. Имеется n + 1 плоскость; n плоскостей проходят через одну и ту же прямую и делят пространство на 2 n равных клиньев (двухгранных углов), а последняя плоскость перпендикулярна к n первым. Эти n + 1 плоскость делят пространство на 4n равных трехгранных углов, к одному из которых применяется метод многократных отражений, использованный в примере 25. Этот метод дает тот же результат: отсекаемый объем максимален, когда поверхность данной площади является порцией сферы с центром в вершине трехгранного угла.

(Существует еще три конфигурации, содержащие трехгранные углы, которым этот метод применим и дает тот же результат. Эти конфигурации связаны с правильными многогранниками; первая — с тетраэдром, вторая — с кубом и октаэдром и третья — с додекаэдром и икосаэдром. Их изучение требует больше усилий или же больше предварительных знаний, и потому мы только перечислим их в следующей таблице, начинающейся с простой конфигурации, описанной выше.

Плоскости	Части пространства	Углы
n + 1	4n	90°	90°	180°/n
6	24	90°	60°	60°
9	48	90°	60°	45°
15	123	90°	60°	36°

«Плоскости» — это плоскости симметрии, «части пространства» — трехгранные углы, и «углы образованы тремя плоскостями, ограничивающими трехгранный угол.)

444

Естественно предположить, что результат остается в силе для любого трехгранного угла. Это предположение индуктивно подкрепляется перечисленными случаями, а также аналогией; сходно полученное сходное предположение относительно углов на плоскости (§ 9) было доказано (пример 19).

Естественно даже распространить это предположение на многогранные углы, и здесь мы можем найти по крайней мере предельный случай, доступный проверке. Назовем здесь «конусом» бесконечную часть пространства, описываемую плоским острым углом, вращающимся вокруг одной из своих сторон. Мы разыскиваем поверхность данной площади, отсекающую от конуса максимальный объем. Можно доказать, что эта поверхность (1) есть поверхность вращения, (2) является порцией сферы и (3) центр этой сферы есть вершина конуса. Мы не можем здесь входить в детали, но следует заметить, что часть (2) доказательства таким же образом вытекает из примета 24, как решение примера 17 вытекает из примера 16. сформулированная в примере 25 задача, поставленная Штейнером, все еще ожидает полного решения.

27. Если бы область площади A имела два биссектора без общей точки, то они делили бы ее на три подобласти, две из которых имеют площадь A/2, а третья — площадь не равную нулю, что, очевидно, невозможно.

28. Прямолинейный отрезок короче: 1 < (π/2)^1/2.

29. См. пример 30.

30. Допустим, что концы данного биссектора лежат на двух различных сторонах, пересекающихся в вершине O, но ни один из концов не совпадает с O. С помощью подходящих отражений (идея рис. 10.12) мы получим шесть равных треугольников, одним из которых является данный биссектор. Эти шесть треугольников образуют правильный шестиугольник с центром O. Эти шесть дух образуют замкнутую кривую, ограничивающую половину площади шестиугольника и, в частности, точку O, в которой пересекаются три оси симметрии кривой. Если длина биссектора минимальна, то замкнутая кривая должна быть окружностью или правильным шестиугольником, в зависимости от того, допускаются ли все биссекторы (настоящий пример 30), или только прямолинейные биссекторы (пример 29); мы должны воспользоваться теоремой II′ примера 8 или, соответственно, теоремой, сопряженной к теореме[280] §7 (1). Решением примера 30 является шестая часть окружности с центром в одной из вершин, решением примера 29 — прямая, параллельная одной из сторон; в каждом случае существуют три решения. Данный биссектор может занимать какое-нибудь другое положение (оба конца на одной и той же стороне или в одной и той же вершине и т. д.), но рассмотрение этих случаев подтверждает полученный результат.

31. [ср. Путнэм 1946]. Пусть O — центр круга. Если прямолинейный отрезок PP′ делится точкой O пополам, то мы будем называть точки P и P′ противоположными одна другой. Мы будем называть две кривые противоположными одна другой., если одна из них состоит из точек, противоположных точкам другой. Пусть теперь A и B — концы биссектора, который мы коротко обозначим AB. Пусть точки A′, B′ и дуга A′B′, соответственно, противоположны A, B и AB. Тогда A′B′ — биссектор. Пусть P — общая точка AB и A′B′. Пусть A, P, P′ и B в этом порядке следуют одна за другой на AB и пусть PB′ — более короткая (не более длинная) из двух дуг PA и PB′. (Этот выбор возможен: фактически он зависит только от обозначений.) Рассматривая кривую, состоящую из двух кусков: дуги B′P (биссектора A′B′) и дуги PB (биссектора AB). Эта кривая (1) короче (не длиннее), чем AB, и (2) длиннее (не короче), чем диаметр BB′, являющийся прямым путем из B в B′, а это и есть теорема.

32. Малая ось. См. пример 33.

33. Кратчайший биссектор любой области есть или прямолинейный отрезок или дуга окружности. См. пример 16. Если область имеет центр симметрии (например, квадрат, круг и эллипс имеют, а равносторонний треугольник не

445

имеет), то кратчайший биссектор есть прямолинейный отрезок. Доказательство почти такое же, как для круга (пример 31).

34. Практически так же, как пример 27.

35. Пример 16.

36. Во всех пяти случаях плоскость кратчайшего биссектора проходит через центр описанной сферы.

Тетраэдр: квадрат в плоскости, параллельной двум противоположным ребрам; 3 решения.

Куб: квадрат в плоскости, параллельной одной из граней; 3 решения.

Октаэдр: шестиугольник в плоскости, параллельной одной из граней; 4 решения.

Додекаэдр: десятиугольник в плоскости, параллельной одной из граней; 6 решений.

Икосаэдр: десятиугольник в плоскости, перпендикулярной оси, которая соединяет две противоположные вершины; 6 решений.

Доказательство в последних четырех случаях очень облегчает одно общее замечание; см. пример 38.

37. Пусть O — центр сферы. Определите противоположные точки и кривые, как в примере 31. Пусть b — биссектор. Тогда и b′, противоположная кривая для b, является биссектором, и b, и b имеют общую точку P (пример 34). Общей точкой является и P′, точка, противоположная P. Точки P и P′ делят b на две дуги, ни одна из которых не может быть короче, чем кратчайшая линия, соединяющая P и P′, являющаяся половиной большого круга.

38. Четыре из пяти правильных многогранников (все, исключая тетраэдр) имеют центр симметрии, Замкнутая поверхность, имеющая центр симметрии, имеет биссектор, который является геодезической линией. Доказательство почти такое же, как для сферы (пример 37).

39. [См. Elemente der Mathematik, 4 (1949), 93 и 5 (1950), 65, задача 65.] Обозначим буквой D расстояние от границы диафрагмы до ее вершины. Площадь диафрагмы равна πd²; это предложение восходит к Архимеду. Ср. пример 11.4.

(1) Если центр шара S является вершиной диафрагмы, то d = a, πd² = πa ².

(2) Пусть l — прямолинейный отрезок, соединяющий центр C шара S и центр C′ сферы, порцией которой является диафрагма. Пусть A — точка пересечения l, соответственно, с диафрагмой и с плоскостью края диафрагмы. Если диафрагма делит пополам объем шара S, то точки A, B, C и D следуют на l одна за другой в этом порядке. Точкой отрезка l, ближайшей к краю диафрагмы, является B, и D дальше от этой границы, чем C. Следовательно, d > a, πd² > πa ².

(3) Предположение: никакая поверхность, делящая пополам объем шара радиуса a, не имеет площади меньшей, чем πa ². доказательство может оказаться трудным.

41. (1) Максимум f = n² достигается, когда

x₁ = x₂ = … = x_n = 1 или — 1.

Минимум f = 0 достигается для бесконечного множества различных систем x₁, …, x_n, когда n ≥ 3.

(2) Максимум такой же, как раньше, и единственный. Минимум f = n достигается, когда

x₁ = n^½, x₂ = … = x_n = 0

и в n — 1 аналогичных случаях.

42. Это предположение верно для правильных многогранников с трехреберными вершинами, но неверно, если вершина имеет больше, чем три ребра. См. Goldberg M., Tôhoku Mathematical Journal, 40 (1935), 226—236.

Нет решения: 40, 43.

446

ГЛАВА XI

1. (a) да, (b) нет: α не необходимы, площадь равна ah/2.

2. (a) да, (b) нет: α и β не необходимы, площадь равна mh.

3. 2πrh независимо от d. Решение с помощью метода Архимеда или с помощью интегрального исчисления: из x² + y² + r² следует

4. Пусть h — высота пояса, площадь которого требуется вычислить. Из подобных прямоугольных треугольников h : a = a :2b, и, таким образом, искомая площадь равна 2πbh = πa² независимо от b. Когда b, = a/2, пояс становится полной сферой, и когда b = ∞, — кру́гом. Ср. пример 10.39.

5. Заметили ли вы аналогию с примерами 1—4? Объем продырявленного шара может быть получен элементарно или путем применения аналитической геометрии и интегрального исчисления как

x² + y² = r², и y₁ есть ордината, соответствующая x = h/2.

6. πh³/12 независимо от a и b. Решение похоже на решение примера 5 и связано с решением примера 7. В крайнем случае (a = b = 0) сегмент превращается в полный шар диаметра h. Если h мало, то разность между Mh и V, интуитивно кажется очень малой.

7. πc³/6 независимо от r. Если c = h, то конус вырождается в цилиндр, и мы имеем случай 2 и пример 5. Решение похоже на решение примера 8.

8. Если O — начало координат и OX =— ось x, то уравнения окружности и параболы на рис 11.3, соответственно, будут

(x — d)² + y² = r², 2px = y².

Пусть x₁ и x₂ обозначают абсциссы точек пересечения этих двух кривых, x₁ > x₂. Тогда x₂ — x₁ = t. Мы воспользовались разложением на множители многочлена второй степени, когда известны два корня и коэффициент при x².

9. (a) да, объем равен πh (a + 2b)/3; (b) нет.

10. Да. Поскольку u₁ и u₂ могут быть заданы произвольно, существует бесконечное множество возможных систем u₁, u₂, …, u₁₀, удовлетворяющих рекуррентному соотношению u_n, = u_{n — 1} + u_{n — 2}. Исследуем две частные системы:

u′₁, u′₂, u′₃, …, u′₁₀ с u′₁ = 0, u′₂ = 1,

u″₁, u″₂, u″₃, …, u″₁₀ с u″₁ = 1, u″₂ = 1.

Находим

u′₇ = 8, u′₁ + u′₂ + … + u′₁₀ = 88, u″₇ = 13, u″₁ + u″₂ + … + u″₁₀ = 143.

Если нам немножко повезет, мы можем заметить, что

u′₁ + u′₂ + … + u′₁₀ = u′₇, u″₁ + u″₂ + … + u″₁₀ = 11u″₇ (*)

и затем догадаться и в конце концов доказать, что

u₁ + u₂ + … + u₁₀ = 11u₇. (**)

447

Доказательство таково: мы непосредственно убеждаемся в том, что соотношение

u_n = (u₂ — u₁) u′_n + u₁ u″_n (***)

выполнено для n = 1 и n = 2 и отсюда заключаем, пользуясь рекуррентной формулой, что оно выполняется и для n = 3, 4, 5, …, 10. Складывая два замеченных равенства (*), после того как первое из них умножено на u₂ — u₁, а второе — на u₁, мы из (***) получаем искомое (**). Главная идея доказательства: общее решение u_n нашего рекуррентного уравнения (более удачно называемого линейным однородным разностным уравнением второго порядка) является общий интеграл линейного однородного дифференциального уравнения второго порядка является линейной комбинацией двух частных интегралов).

независимо от α. При переходе от второй формы к третьей мы ввели в качестве новой переменной интегрирования x^—1. Для α = 0, ∞, — ∞ данный интеграл сводится, соответственно, к

Эти случаи могли бы натолкнуть на приведенное выше решение.

12. Вот наиболее очевидный факт этого рода[165]:

Положим u = ln x, f(ln x) = F (x):

Это подсказывает следующее обобщение:

h(x^–1) = – h(x).

Пример 11 является частным случаем:

13. 0x = 0, или x² — 4 = (x — 2) (x + 2) и т. д.

14. x = y = 8; достаточно испытать x = 8, 9, 10, 11.

448

15. x = y = z = w = 4 с помощью проб.

17. [Ср. Стэнфорд 1948]. Плоскости симметрии правильного многогранника проходят через его центр и делят сферу с тем же центром на сферические треугольники. Три радиуса, соединяющие с центром три вершины этого сферического треугольника, проходят, соответственно, через вершину, центр грани и середину стороны. Соответствующие углы сферического треугольника равны π/v, π/f и π/2. Обозначим буквой c сторону (гипотенузу) сферического треугольника, противоположную углу π/2. отношение радиуса вписанной сферы к радиусу описанной сферы равно cos c, и по формуле сферической тригонометрии

cos c = ctg(π/f)ctg(π/v).

Числа f, v и получающееся в результате значение cos c представлены в следующей таблице для тетраэдра, гексаэдра (куба), октаэдра, додекаэдра и икосаэдра:

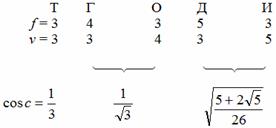
Вейль Г., Симметрия, М., 1968; см. там стр. 103, рис. 46, воспроизводящий оригинальный чертеж Кеплера.

18. См. пример 10. 42.

21. (a) Определитель n-го порядка мы назовем центрально-симметричным, если его элементы a_j,k удовлетворяют условию

a_{j, k} = a_{n + 1 – j, n + 1 – k} для j, k = 1, 2, 3, …, n.

Центрально-симметричный определитель n-го порядка является произведением двух определителей. В зависимости от того, четно n или нечетно или оба множителя n./2-го порядка или один множитель (n + 1)/2-го порядка, а другой — (n — 1)/2-го порядка. Примеры:

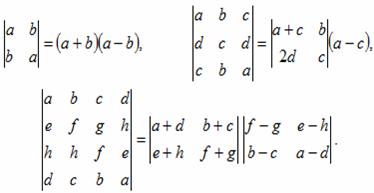
Доказательство: В зависимости от того, четно n или нечетно, положите n = 2m или n = 2m + 1. Прибавьте последний столбец к первому, предпоследний ко второму и т. д., пока не изменятся первые m столбцов. После этого вычтите первую строку из последней, вторую из предпоследней и т. д., пока не изменятся последние m трок. Эти операции приводят или к прямоугольнику m × (m + 1) или к квадрату m × m в юго-западном углу, состоящему из нулей[281].

(b) Определитель четвертого порядка мог бы делиться на оба определителя второго порядка и не будучи их произведением, именно если бы эти определители второго порядка имели общий множитель. Будучи оптимистами, мы допустили, что такого общего множителя нет: мы попробовали самое простое допущение и добились успеха.

Наиболее оптимистическая возможность: коэффициент при любой степени h в левой части неравенства меньше или равен коэффициенту при той же

449

степени в правой части неравенства. Это действительно имеет место: после деления на 4h^¼ постоянный член становится равным 1 в обеих частях и для n ≥ 1 коэффициенты при hⁿ в соответствующих частях равны

Очевидно

3·7·11 … (4n — 1) < 5·9 … (4n — 3) (4n + 1).

23. (a)Обозначим символом P_n приближенное значение, полученное рассматриваемым методом, когда квадрат подразделен на n² меньших квадратов. Допустим, что P_n можно разложить по степеням n^—1:

P_n = Q₀ + Q₁ n^—1 + Q₂ n^—2 + …

(«Вообще говоря, функция может быть разложена в степенной ряд». Ср. пример 20.) Когда n → ∞ P_n → 0, и мы заключаем, что Q₀ = Q. Далее, четыре точки на рис 11.6 ближе к прямой, чем точки на рис 11.5. Это обстоятельство наталкивает на мысль Q₁ = 0 и члены с n^—3, n^—4, … пренебрежимо малы даже при мало n. Это приводит к соотношению

P_n ~ Q + Q₂n^—2,

что изображается, если мы возьмем n^—2 в качестве абсциссы, а P_n в качестве ординаты, прямой линией (приближенно). В некоторых более или менее сходных случаях было доказано, что погрешность приближения имеет порядок 1/ n², и в свете такой аналогии наша догадка кажется менее дикой.

(b) Столбцы нижеследующей таблицы содержат: (1) значения n, (2) ординаты, (3) разности ординат, (4) абсциссы, (5) разности абсцисс, (6) наклоны, вычисленные как отношение (3) к (5), при этом в (5) и (6) знак опущен:

(1)	(2)	(3)	(4)	(5)	(6)
2	0,0937		0,2500
		0,0248		0,1389	0,1785
3	0,1185		0,1111
		0,0094		0,0486	01934
4	0,1279		0,0625
		0,045		0,0225	0,2000
5	0,1324		0,0400

(c) Естественно в качестве наиболее надежного вычисления рассматривать n = 5, а в качестве следующего наилучшего n = 4. Если точки (x₁, y₁) и (x₂, y₂) лежат на прямой с уравнением y = mx + b, то мы легко находим (из системы двух уравнений относительно m и b)

что в настоящем случае дает

Если вы ожидали что-нибудь лучшее, чем это, то вы слишком оптимистичны.

Нет решения: 16, 19, 20.

450

ГЛАВА XII

1. Сходство с таблицей § 3.12 (разбиения пространства) можно рассматривать как большее. Все упомянутые таблицы за исключением таблицы § 3.1 в которой перечислены многогранники, относятся к индуктивным доводам, подкрепляющим предположение A специальной природы: A говорит, что некоторое утверждение S_n, значение которого зависит от переменного целого числа n, истинно для n = 1, 2, 3, … Индуктивное исследование такого предположения A естественно происходит в известном порядке: сначала мы испытываем S₁, затем S₂ затем S₃ и т. д. Этот порядок виден в устройстве таблиц. Однако если мы исследуем предположение, относящееся к многогранникам, как в §3.1, то никакого такого «естественного прядка нет. Наше исследование мы можем начать с тетраэдра, который с различных точек зрения можно рассматривать как «самый простой» многогранник. Но какой многогранник мы должны исследовать за ним? Нет никаких убедительных оснований рассматривать какой-нибудь многогранник как «второй по простоте», другой как третий и т. д.

2. Случаи 101 и 301 кажутся «более далекими» от уже проверенных случаев 1, 2, 3, …, 20, чем случаи 21 и 22 (и в исследовании Эйлера они действительно кажутся такими); представляется разумным (и это, несомненно, находится в согласии со схемой, введенной в § 2) больше веса придать подтверждению случаев 101 и 301, чем подтверждению случаев 21 и 22.

3. (1) c = p: треугольник вырождается в прямолинейный отрезок; A = 0.

(2) c > p делает A мнимым: нет треугольника с c > p.

(3) a = b = c: треугольник равносторонний и A² = 3a⁴/4, что правильно.

(4) a² = b² + c²: треугольник прямоугольный и

16A² = (a + b + c) (b + c + a) (a — b + c) (a + b — c) =

= [(b — c)² — a²] [a² — (b — c)²] = 2bc².

Или A² = bc²/4, что правильно.

(5) b = c = (h² + a²/4)^1/2: треугольник равнобедренный с высотой h и

16A² = (a + 2b) (2b — a)a² = (4b² — a²) a² = 4h²a²,

что правильно.

(6) Размерность правильная.

(7) Выражение для A² симметрично относительно трех сторон a, b и c, как и должно быть.

4. (1) d = 0: четырехугольник превращается в треугольник, утверждаемая формула сводится к формуле Герона, пример 3.

(2) d = p: четырехугольник вырождается в прямолинейный отрезок; A = 0.

(3) d > p делает A мнимым: нет четырехугольника с d > p.

(4) a = b = c = d дает A² = a⁴, что правильно для квадрата, но неправильно (слишком велико) для ромба: квадрат можно вписать в круг, ромб нельзя.

(5) c = a, d = b дает A² = (ab) ², что правильно для прямоугольника, но неправильно (слишком велико) для косого параллелограмма: прямоугольник можно вписать в круг, косой параллелограмм нельзя.

(6) В предыдущих случаях (4) и (5) утверждаемая формула приписывает площади четырехугольника, который нельзя вписать в круг, слишком большое значение: это согласуется с § 10.5 (2) и § 10.6 (3).

(7) Утверждаемая формула дает правильную размерность A.

(8) Согласно утверждаемой формуле, A симметрично[282] относительно четырех сторон a, b, c и d: вписанный четырехугольник остается вписанным в тот же круг, если переставляются две его соседние стороны. (Рассмотрите четыре равнобедренных треугольника с общей вершиной в центре круга, основаниями которых являются четыре стороны.)

451

Эти замечания, конечно, не доказывают предложенной формулы, но, в соответствии со схемой, представленной в § 2, они делают ее очень правдоподобной. Для доказательства см. пример 8.41.

5. (1) a = b = c = e = f = g: тетраэдр правильный; V = 2^1/2a³/12.

(2) e² = b² + c², f² = c² + a², g²= a² + b²: тетраэдр «трижды прямоугольный», т. е. ребра a, b и c, начинающиеся из одной и той же вершины попарно перпендикулярны; V = abc/6.

(3) e = 0, b = c, f = g: тетраэдр сплющивается, становится плоской фигурой — треугольником; V = 0.

(4) e = a, f = b, g² = c² = a² + b² тетраэдр сплющивается, становится прямоугольником со сторонами a и b; V = 0.

(5) Частный случай, более широкий, чем (4): тетраэдр становится плоским четырехугольником со сторонами a, b, e, f и диагоналями c, g. Тогда V = 0 дает соотношение между сторонами и диагоналями общего четырехугольника, которое можно непосредственно, хотя и с несколько бо́льшим трудом, подтвердить.

(6) Размерность правильная)

(7) Выражение объема V не симметрично относительно всех шести ребер, но оно и не обязано быть симметричным: три ребра a, b, c, начинающиеся из одной и той же вершины, играют не ту роль, которую играют три ребра e, f, g, образующие треугольник (грань). Мы можем, однако, преобразовать предложенное выражение в следующее:

144V² = a²e²(b² + f² + c² + g² — a² — e²) + b²f²(b² + g² + a² + e² — b² — f²) +

+ c²g²(a² + e² + b² + f² — c² — g²) — e²f²g² — e²b²c² — a²f²c² — a²b²g².

Первые три строки соответствуют трем парам противоположных ребер, четыре члена в последней строке — четырем граням тетраэдра: новая алгебраическая форма выявляет всю симметрию (взаимозаменяемость) данных, присущую геометрической конфигурации. между прочим, новая форма (правильность алгебраических преобразований, которые к ней привели) также може быть проверена с помощью частных случаев (1), (2), (3), (4).

6. (1) Мы находим для s₁, s₃, s₅, q, r, соответственно, числовые значения 6, 36, 276, 11, 6, которые подтверждают обе формулы.

(2) Более общий случай. Пусть

a + b + c = s₁ = p = 0.

Тогда

s₃ = — 3ab (a + b), s₅ = — 5ab(a + b)(a² + ab + b²), q — a² — ab — b², r = — ab(a + b),

и обе формулы подтверждаются, так как

(3) Более общий случай. Пусть c = 0. Длинные прямые вычисления подтверждают обе формулы.

(4) Более общий случай. Пусть b + c = 0. Тогда s₁ = a, s₁ = a³, s₅ = a⁵: в выражениях, предложенных для q и r, обращаются в нуль знаменатель и числитель.

Для доказательства и обобщения см. Journal des math. pures et appliquées, ser. 9, 31 (1952), 37—47.

7. Утверждение B₄ (с r = h = 0) содержится как частный случай и в B₂ (r = 0) и B₃ (h = 0). Следовательно, если B₂ или B₃ истинно, то и B₄ должно быть истинно. Если мы ясно об этом помним, то подтверждение B₄, пришедшее после подтвержденияB₂ или B₃, не дает нам новой информации. А где нет новой информации, там не может быть новых доводов, как я думаю. Тем не менее желательно отметить B₄: оно дорисовывает картину.

452

8. Более тщательное рассмотрение вывода п. 9—13 мемуара Эйлера в § 6.2 показывает, что C*₁, C*₂, …, C*₂₀ математически следуют из C₁, C₂, …, C₂₀: поэтому подтверждение C₁*, C₂*, …, C₂₀* фактически не дает новой информации или доводов, а подтверждение C*₁₀₁, C*₃₀₁, дает.

9. Эта схема, в сущности, совпадает со схемой, которая будет введена в примере 11; см. там замечания.

10. Если 8n + 3 = w² + 2p, то целое число w обязательно нечетно. Поэтому w² имеет вид 8n + 1, и, таким образом, p имеет вид 4n + 1. Эйлер доказал, что

p = u² + v².

Из двух целых чисел u и v одно должно быть четным, а другое — нечетным. Отсюда

2p = 2u² + 2v² = (u + v)² + (u — v)².

Все три числа, w, u + v и u — v нечетны. Пусть

w = 2x — 1, u + v = 2y — 1, u — v = 2z — 1,

и мы получаем

8n + 3 = (2x — 1)² + (2y — 1)² + (2z — 1)²,

или

13. Да, должна, в согласии со схемой, введенной в § 6.

Нет решения: 11, 12, 14.

ГЛАВА XIII

1. Следующая схема всегда применима:

Из A следует B

B ложно

A ложно

Примените ее, подставив не-B вместо B. Вы получите

Из A следует не-B

Не-B ложно

A ложно

Мы отметили в § 4 (5) эквивалентность:

«Из A следует B» экв. «A несовместно с не-B».

И эта эквивалентность всегда применима. Примените ее, подставив не-B вместо B. Вы получите

«Из A следует не-B» экв. «A несовместно с B».

Мы приняли здесь без доказательства, что отрицание не-B есть B (так как отрицание B не есть B), и поэтому подставили B вместо не-(не-B). Подставляя B вместоA в эквивалентность, отмеченную в конце § 4 (3), мы также получаем

«Не-B ложно» экв «B истинно».

Подставляя вместо двух посылок последней схемы соответствующие эквивалентные утверждени, стоящие в правых частях двух предыдущих эквивалентностей,

Получаем

A несовместимо с B

B истинно

A ложно

Это действительно доказательная схема из § 3.

2. Допустим, что всегда применима следующая схема:

Из A следует не-B

B истинно

A более правдоподобно

Примените ее, подставив не-A вместо A и не-B вместо B. Вы получите

Из не-A следует не-B

не-B истинно

Не-A более правдоподобно

Соберите следующие три эквивалентности:

«Из не-A следует не-B» экв. «Из B следует A»,

«Не-B истинно» экв. «B ложно»,

«Не-A более правдоподобно» экв. «A менее правдоподобно».

Первая выведена в § 4 (5). Вторая была упомянута в § 4 (3), в других обозначениях, с A вместо B. Третья была высказана (придумана именно для настоящей цели) в § 5. подставьте вместо посылок и заключения последней рассмотренной схемы три только что выписанных эквивалентных утверждения. Вы получите:

Из B следует A

B ложно

A менее правдоподобно

Если не считать легких изменений в словах (или обозначениях), это действительно эвристическая схема, введенная в § 2.

3. Начните с той же схемы, что и в примере 2. подставьте не-B вместо B (как в примере 1). Таким образом вы получите:

Из A следует не-B

Не-B истинно

A более правдоподобно

Соберите следующие две эквивалентности:

«Из A следует не-B» экв. «A несовместно с B»

«Не-B истинно» экв. «B ложно»

Первая была выведенав при мере 1. вторая с некоторым изменением обозначений (A вместо B) дана в § 4 (3). Подставьте вместо двух посылок рассмотренной схемы только что выписанные эквивалентные утверждения. Вы получите:

A несовместно с B

B ложно

A более правдоподобно

Это действительно эвристическая схема из § 3.

4. (a) Во всяком случае, из A следует B, где утверждение B определяется следующим образом:

B. Буквы, по которым искомое восьмибуквенное слово пересекается с другими словами кроссворда, выбраны из букв слова ВЕРНОСТЬ.

454

Будем понимать B как относящееся к двум клеткам, заполненным в предложенной диаграмме (предпоследняя и третья от начала). Мы должны различать два слчая.

Если мы рассматриваем решение для двух пересекающих слов как окончательное, то мы находим, что B истинно и таким образом мы подтвердили следствие предположения A. Поэтому в соответствии с фундаментальной индуктивной схемой (§ 12.1) мы рассматриваем A как более правдоподобное.Если, однако, мы рассматриваем решения для пересекающих слов только как предположительные, то мы сделали B только более правдоподобным. Поэтому подходит затушеванный вариант фундаментальной индуктивной схемы, определенный в § 6, и, конечно, доводы в пользу A слабее, чем в первом случае.

(b) РЕВНОСТЬ.

5. Схема из § 13 (5):

Factum Probans весьма правдоподобно или его можно понять при допущении Factum Probandum.

Factum Probans (совсем) не в такй мере правдоподобно или его трудно понять без допущения Factum Probandum.

Самое Factum Probans доказано

Это делает Factum Probandum более правдоподобным.

Настоящее изложение кажется более пригодным для суда, но изложение в § 10 более пригодно для того, чтобы показать связь с наиболее обычной формой индуктивного рассуждения в физических науках и в математическом исследовании.

6. Обвинение мы должны трактовать как предположение:

A. Плата наличными за автомобиль чиновника была произведена из кармана подрядчика.

Мы должны рассматривать как факт:

B. Взятая со счета подрядчика сумма (875 долларов) равна плате за автомобиль чиновника, дата взятия предшествует дате платы на два дня[283].

B вместе с A значительно легче понять, чем B без A: если взятие денег со счета не связано с последующей платой, то точное совпадение сумм и близость дат следует приписать простой случайности. Такая случайность не невозможна, но невероятна. Сила улик зависит от этого обстоятельства. Вполне подходит схема из § 13 (5).

7. Назовем бедных м-с Белую и м-ра Черного «обвиняемыми» (они не могут ответить на обвинение, но они по крайней мере могут быть подвергнуты перекрестному допросу м-с Зеленой[284].) Обвинение м-с Зеленой, если содрать с него ее благочестивое многословие, конечно, таково:

A. Обвиняемые совершают двойное прелюбодеяние.

Мы принимаем как факт: B: Обвиняемые вели в темноте продолжительный разговор через изгородь

Этот факт, к несчастью, дает некоторую косвенную улику в пользу A в соответствии с разумной схемой [§ 13 (5)], если принять следующие две посылки:

B вместе с A весьма правдоподобно,

B без A не в такой мере правдоподобно.

Я опасаюсь, что бесполезно пытаться поколебать веру Пригородска в первую посылку. Однако даже некоторые пригородцы могут понять, что в этот злополучный вечер обвиняемые вполне могли бы обсуждать договор об аренде, в котором и тот, и другая законно заинтересованы. Это делает B в такой же мере правдоподобным без A, как и вместе с A, опрокидывает вторую посылку, объясняет и делает несостоятельной предполагаемую косвенную улику. Это рассуждение может оказаться бесполезным против сплетен м-с Зеленоой, хотя мне оно кажется разумным и типичным. Выступая против какой-нибудь части косвенных улик, адвокаты очень часто пытаются в «опровержении» опрокинуть именно эту вторую посылку рассматривамой схемы.

455

8. Мы должны рассмотреть другое утверждение или предположение:

B. Подсудимый был хорошо знаком с жертвой за три года до преступления.

Было бы слишком сильно сказать, что из B следует A, но более слабое утверждение в этом направлении, очевидно, оправдано:

B делает A более правдоподобным.

Теперь C не доказывает B, но, несомненно, делает B более правдободобным. Из двух выписанных посылок невользоохочется сделать вывод:

A более правдоподобно.

Это, по-видимому, подсказывает новую схему:

A более правдоподобно вместе с B

B более правдоподобно

A более правдоподобно

Первая посылка этой схемы слабее, чем соответствующая посылка схемы во 2 строки и столбце (2) таблицы I, вторая посылка такая же: заключение также должно быть слабее. [См., однако, пример 15.2]

Кстати, существенна величина фирмы: если фирма мала, то B делается более правдоподобным, чем в противном случае.

Нет решения: примеры от 9 до 20.

ГЛАВА XIV

1. (a) Следует из r_r + s_r = r_s = s_s = 1.

(b) r_r — r_s = s_s — s_r < 0.

2. С подходящим образом приспособленными обозначениями примера 1 r_r — r_s = s_s — s_r < 0.

3. , где N = 26 306, n = 12, p = ⅓, q = ⅔ и s — число в той же строке в столбце (1).

4. То же выражение, что и в решении примера 3 с теми же числовыми значениями для N и n и с тем же значением s, но p = 0,3376986, q = 1 — p.

5. (a) Nμ^se^-μ/s!, где N = 30, μ = 10, и s — соответствующее число в столбце (1).

(b) — — — + + — — + — — — +++ — + — +++.

6. 6^—3n.

7. Составное событие, состоящее в выпадении шести очков на каждой игральной кости пять раз без перерыва, при гипотезе честных костей имеет вероятность 6^—15; n = 5 в примере 6.

где β = — α = 0,5 (pgn)^—1/2 и y, p, q и n имеют то же значение, что и в (а)[285]. Чтобы вычислить числовые значения с такой точностью, как они здесь даны, простейших распространенных таблиц интеграла вероятности недостаточно.

9. Появления в выборке соответственно ни одного дефектного изделия, только одного дефектного изделия, точно двух дефектных изделий, …, точно с дефектных изделий.

456

§ 8(1).

11. Искомая вероятность равна 10 ^{— n}, в предположении, что мы принимаем то или иное из следующих допущений:

(I) Все возможные последовательности из n цийр равно вероятны. (Имеется 10ⁿ таких последовательностей).

(II) Различные цифры в последовательности взкаимно независимы, и для каждой цифры равно вероятны десять возможных случаев: 0, 1, 2, …, 9. (Несколько раз примените правило из § 3(5).)

Оба допущения выглядят «естественно», но ни одно из таких допущений не является логически необходимым: ответ 10^—n, хотя он и очень напрашивается, не является математически определенным.

12. Допустите, что l различных букв могут быть вытащены из мешка соответственно с вероятностями p₁, p₂, …, p_l. Мы имеем два таких мешка и вытаскиваем букву из каждого: вероятность совпадения равна p²₁, p²₂, …, p²_l, В случае гипотезы II, l = 17 и p₁, …, p₁₇ могут быть найдены фактическим подсчетом.

13. В обоих случаях

где q = 1 = p; (a) p = 0,0948, (b) p = 1/26 = 0,03846.

14. В обоих случаях np, где p = 0,0948, (a) n = 450, (b) n = 90.

15. (npq)^1/2 для n = 90, p = 0,0948, q = 1 — p. Вычисление стандартного отклонения 7,60 основано на формуле, которую нельзя найти в учебниках. В обозначениях примера 12 положим

σ² = n(n — 1)ω[p(1 — p) + 2(n — 2)(p′ — p²)]/2.

Тогда n = ω = 10, p = 0,0948, p′ = 0,01165 дают σ = 7,60.

16. Допустим, что 60 испытаний с монетой независимы, и применим многократно правило, выведенное в § 3(5).

17. Обобщите предложенную числовую таблицу

s	r	n
s′	r′	n′
S	R	N

и интерпретируйте ее следующим образом. Имеется N = R + S = n + n′ карт, среди которых R = r + r′ карт красных и S = s + s′ карт черных. Карты наугад распределяются между двумя игроками: один получает n карт, а другой — n′ карт. Какова вероятность того, что первый игрок получит r красных карт и s черных карт, а другой игрок r′ красных карт и s′ черных карт? Конечно, r + s = n, r′ + s′ = n′.)[286] Ответ, как хорошо известно, таков:

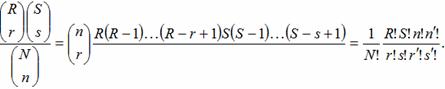
Из девяти величин, содержащихся в таблице, только четыре могут быть заданы

457

произвольно, значения остальных пяти величин следуют из написанных выше соотношений. Возьмем числа n = 9, n′ = 11 и S = 8 как данные (число пациентов, лечившихся по каждому методу, и общее число смертельных исходов), из чего следует N = 20 и R = 12. Однако для s′ мы последовательно возьмем s′ = 2, 1, 0 (число смертельных исходов при втором методе лечения ≤ 2). По нашей формуле мы вычисляем вероятность в каждом из этих трех случаев (не больше двух смертельных исходов при лечении по новому методу, 2, 1 или 0 черных карт у м-ра Нового) и, складывая вероятности этих взаимно исключающих событий, находим:

[287].

18. В силу очевидного распространения рассуждения из § 3 (5) (трехмерный аналог рис 14.2) число возможных случаев равно n³. Все благоприятствующие случаи, т. е. все допустимые решения уравнения Z = X + Y, можно перечислить следующим образом:

2 = 1 + 1,

3 = 1 + 2 = 2 + 1,

4 = 1 + 3 = 2 + 2 = 3 + 1,

......................

n = 1 + (n — 1) = 2 + (n — 2) = … = (n — 1) + 1.

21. Вероятность того, что выборка, состоящая из 38 человек из бесконечного населения будет содержать 30 или более психически ненормальных людей равна

предполагая, что психически ненормальные составляют 100p% = 1% населения. Оцененная вероятность есть правдоподобие утверждения газеты в свете наблюдения чиновника, вычисленное при простейших допущениях.

22. Искомая вероятность равна

(Любые из четырех часов могли бы оказаться теми из трех часов, находящихся в согласии, которые показывают наиболее раннее время. то, что все четверо часов могут показывать время с расхождением меньше, чем на 2 мин., объясняет первый член в фигурных скобках[166].)

458

23. Целое число a принимает одно из значений

— n, …, — 2, — 1, 0, 1, 2, …, n.

Допустим, что эти 2n + 1 значений равновероятны, сделаем соответствующее допущение для a, b, c, d, e и f и допустим также, что a, b, c, d, e и f взаимно независимы. Теперь, придав точный смысл словам «выбраны наугад», мы можем приступить к решению задачи.

Точно одно решение существует в том и только в том случае, если ad — bc ≠ 0. Мы можем пренебречь и пренебрежем e и f: существует (2n + 1)⁴ возможных случаев. Подсчитаем неблагоприятствующие случаи, различая две возможности.

(I) a = 0. Тогда bc = 0, d произвольно и существует (2n + 2n + 1) (2n + 1) случаев.

(II) a ≠ 0. Тогда a может принимать 2n значений, b и c произвольны и d однозначно определяется значениями a, b и c : существует 2n(2n + 1) случаев [167].

Искомая вероятность равна

и, таким образом, когда n стремится к ∞, она стремится к 1. Это придает другой точный смысл утверждению: система двух уравнений с двумя неизвестными, вообще говоря, имеет только одно решение». Ср. § 11.3, пример 11.16.

24. Подтверждение Ы больше увеличило бы[288] нашу веру в слово ВЫШКА[289], чем подтверждение К. Так как Ы встречается реже, чем К[290], то появление Ы в пересекающем слове труднее истолковать как случайное совпадение, чем появление К.

25.Составляя таблицу разностей между последовательными числами каждого столбца, а затем снова разностей разностей (так называемых «вторых разностей»), получаем

I			II
1005			1004
	28			34
1033		+ 14	1038		0
	42			34
1075		— 11	1072		0
	31			34
1106		— 5	1106		— 1
	26			33
1132		+ 21	1139		+ 1
	47			34
1179		— 21	1173		— 1
	26			33
1205		0	1206		0
	26			33
1231		+ 17	1239		— 1
	43			32
1274		— 16	1271		0
	27			32
1301			1303

459

Первые разности достаточно ясно показывают, что II столбец правильный, а I — неправильный, но вторые разности более красноречивы: II обнаруживает минимум неправильности, вызываемой неизбежными погрешностями округления, но вторые разности в I меняют знак и очень велики. Такое «вычисление разностей» является важной операцией при контроле составления числовых таблиц. Имеются два замечания.

(1) В Таблице функции f(x) первые разности в силу теоремы о среднем значении связаны с f′(x). Это дает нам возможность контролировать разности.

(2) Последние цифры в I в действительности являются первыми десятью десятичными знаками числа π, взятыми в обратном порядке. Точка зрения, что последовательные десятичные знаки числа π ведут себя так, как будто они были получены случайно, выражалась много раз и с многими вариациями.

27. Допустим, что A независимо от B:

P{A} = P{A/͞B} (6)

(мы начинаем с (6), чтобы избежать смешения с нумерацией в примере 26).

Пользуясь (4), (2), (6) и (3) (в этом порядке), получаем

P{A} = P{A/B} + P{A/͞B}= P{B}P{A/B} + P{͞B}P{A/͞B} =

= P{A/B}(P{B} + P{͞B}) = P{A/B}. (7)

Из (2), (7) и P{A} ≠ 0 следует, что

P{A}P{B/A} = P{B}P{A}, P{B/A} = P{B} (8)

.

Снова пользуясь (4) и (2), как в (7), и пользуясь также (8), 3 и P{͞A} ≠ 0, находим, что

P{B} = P{A}P{B/A} + P{͞A} P{B/͞A},

(1 — P{A})P{B} = P{͞A}P{B/͞A}, (9)

P{B} = P{B/͞A};

(6), (7), (8) и (9) доказывают требуемое заключение.

28. Если A и B взаимно независимы, то

P{AB} = P{A}P{B}.

Это следует из правила (2) примера 26 и определения (II) примера 27.

29. (a) P{A}, P{A/B}, P{A/͞B}, P{B}, P{B/A}, P{B/͞A}.

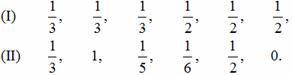
(b) P{AB} = P{A}P{B/A} = P{B}P{A/B}.

460

(c) Общие формулы следуют из примера 26 (4), (2). Численно:

P{A} = P{B}P{A/B} + P{͞B}}, P{A/͞B},

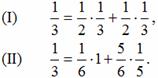
P{B} = P{A}P{B/A} + P{͞A}}, P{B/͞A},

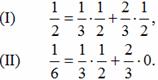
(d) В (I) A и B взаимно независимы, в (II) — нет.

Нет решения: 19, 20, 26, 30, 31, 32, 33.

ГЛАВА XV

1. Так как их H следует и A, и B, то P{A/H} = 1, P{B/H} = 1. Следовательно, по правило (2) примера 14.26,

P{H} = P{A}P{H/A}, P{H} = P{B}P{H/B},

Исключая P{H}, получаем

P{A}·P{H/A} = P{B}·P{H/B}.

Если мы рассмотрим связь между H и A, а также связь между H и B как неизменную и, следовательно P{H/A} и P{H/B} как постоянные и если P{B} будет возрастать, то в силу последнего равенства и P{A} будет возрастать.

2. По формулам (2), (3), (4) примера 14.26

P{A} = P{A/͞B} + P{B}(P{A/B} — P{A/͞B}).

Примем P{A/B} и P{A/͞B} как заданные, но пусть P{B} возрастает. (Это можно вполне естественно себе представить в случае, рассмотренном в примере 13.8.) Возрастание P{B} влечет за собой соответствующее возрастание P{A}, если

P{A/͞B} > P{A/͞B}.

В конкретном случае примера 13.8 это неравенство кажется приемлемым. Однако формулировка схемы, приведенной в решении примера 13.8 кажется неприемлемой. Вот формулировка, которая выглядит лучше и, несомненно, находится в согласии с нашей формулой:

A более правдоподобно вместе с B, чем без B

B (становится) более правдоподобно

A (становится) более правдоподобно

Если A является следствием B, то P{A/͞B} = 1, формула (*) несомненно правильна и схема превращается в схему § 13.7, таблица I, строка 2, столбец 2.

3. Просмотрите несколько случаев, в которых мы изложили схемы правдоподобных рассуждений с помощью исчисления вероятностей: §§ 6—10 и примеры 1—2. Монотонность и непрерывность, утверждаемые примером 13.10, в этих случаях очевидны ввиду следующего простого математического факта: если a, b, c, d, x₁, x₂ — действительные постоянные, ad — bc ≠ 0, и функция y от x определяется формулой

461

и обладает тем свойством, что при x₁ < x < x₂ выполнены неравенства 0 ≤ y ≤ 1, то y строго монотонна и непрерывна при x₁ ≤ x ≤ x₂. Что касается общности замечаний примера 13.10, то мы должны заметить следующее: если y не дробно-линейная, а (более общая) рациональная функция от x, то она все еще необходимо остается непрерывной функцией от x, за исключением точек, где ее знаменатель обращается в нуль, но не является более непременно монотонной функцией[291].

Нет решения: 4, 5, 6, 7, 8, 9.

ГЛАВА XVI

2. [Стэнфорд 1951]. Четырехугольник должен быть выпуклым. Обозначим цифрами I, II, III, IV треугольники, на которые он делится своими диагоналями. Пусть (I), (II), (III), (IV) — соответственно площади этих четырех треугольников и p, q, r, s — длины четырех прямолинейных отрезков, соединяющих точку пересечения диагоналей с четырьмя вершинами четырехугольника. Номера и буквы идут в «циклическом порядке», так что сторона длины p является общей для IV и I, q — для I и II, r — для II и III, s — для III и IV; I противоположен III, II противоположен IV; p + r есть длина одной диагонали, q + s — другой. Пусть p и q заключают угол α. Тогда

2(I) = pq sin α, 2(II) = qr sin α, 2(III) = rs sin α, 2(IV) = sp sin α.

Отсюда

(a) (I)(III) = (II)(IV).

(b) Основание I параллельно основанию III в том и только в том случае, если

p/q = r/s, или (II) = (IV).

(c) Четырехугольник является параллелограммом в том и только в том случае, если

p =q, r = s, или (I) = (II) = (III) = (IV).

3. [Стэнфорд 1949]: (a) Пусть a — сторона равностороннего треугольника. Соединяя точку внутри него с его тремя вершинами, вы делите треугольник на три треугольника с площадями, которые, будучи сложены вместе, дают всю площадь: ax/2 + ay/2 + az/2 + ah/2. Разделите на a/2. См. рис 8.8.

(b) Точка, лежащая внутри правильного тетраэдра с высотой h, имеет расстояния от его четырех граней, соответственно, x, y, z и w. Тогда x + y + z + w = h. Доказательство аналогично: разделите правильный тетраэдр на четыре тетраэдра.

(c) Соотношение остается справедливым в обоих случаях (a) и (b) для внешних точек, при условии, что расстояния x, y, z и w берутся с надлежащим знаком: +, когда зритель, находящийся в данной точке, видит сторону (грань) изнутри, — когда он видит ее извне. Доказательство по существу такое же.

4. [Стэнфорд 1946]. (a) (I) и (IV) верно всегда, но (II) и (III) — нет; см. (b)

(b) (II) и (III) неверны: противоречащие примеры соответственно дают прямоугольник и ромб.

(c) (II) и (III) верны для пятиугольников.

(d) (II) и (III) верны для многоугольников с нечетным числом сторон, 3 или 5, или 7 …, что следует из (II′) и (III′).

(II′) Если многоугольник, вписанный в окружность, равноугольный, то любые две стороны, отделенные только одной промежуточной стороной, равны. Следовательно, если число сторон четно, равно 2m, то либо все 2m сторон равны, либо же m сторон равны a, а остальные m сторон равны b, a ≠ b, и никакие две стороны, имеющие общую вершину, не равны.

(III′) Если многоугольник, описанный вокруг окружности, равносторонний, то любые два угла, отделенные ьтолько одним промежуточным углом, равны. Следовательно, если число углов четно, равно 2m, то либо все 2m сторон равны,

462

либо же m углов равны α, а остальные m углов равны β, α ≠ β, и никакие два угла, имеющие общую сторону, не равны.

Чтобы доказать (I), (II), (III) и (IV), соедините центр окружности с вершинами многоугольника, опустите перпендикуляры из центра на стороны и подберите конгруэнтные треугольники.

5. [Стэнфорд 1947]. Отношение между (a) и (b) кажется сходным с отношением между (b) и (c). Такой переход существует, если

α + β + γ = π,

2α + 2β + 2γ = 2π ≠ π, но

(π — 2α) + (π — 2β) + (π — 2γ) = π.

Приняв без доказательства, что (a) имеет место для любых трех углов α, β, γ с суммой π, мы получим (b), подставив вместо этих углов, соответственно, π — 2α, π — 2β, π — 2γ. Мы переходим от (b) к (c), пользуясь той же подстановкой.

Остается проверить (a), что можно сделать многими способами, например, следующим. Подставляя вместо α, β и γ соответственно 2u, 2v и π — 2u — 2v, мы преобразуем (a):

sin u cos u + sin v cos v = [2 cos u cos v — cos (u + v)] sin (u + v).

Воспользуйтесь теоремами сложения для косинуса и синуса.

[Стэнфорд 1952]. Согласно четырем предположениям, объем усеченной пирамиды был бы равен, соответственно,

(I) [(a + b)/2]²h,

(II) [(a² + b²)/2]²h,

(III) [a² + b² + (a + b)²/4]²h/3,

(IV) [a² + b² + ab]²h/3.

Если b = a, то усеченная пирамида превращается в призму с объемом a²h: в этом отношении (I), (II), (III), (IV) находятся в согласии и дают правильный результат. Если b = 0, то усеченная пирамида превращается в пирамиду с объемом a²h/3: это дает только(IV) и, таким образом, (I), (II), (III), дающие значения, должны быть неправильны. То, что(IV) вообще правильно, еще должно быть доказано; см. учебники.

10. (1) Производя сложение с помощью бумаги и карандаша наиболее обычным способом, вы начинаете с верхней цифры в последнем столбце и спускаетесь вниз; вот первые два шага в данном примере: 3 + 7 = 10, 10 + 0 = 10. Затем вы спускаетесь по второму столбцу и т. д. (2) Вы берете столбцы в том же порядке, как и прежде, но начинаете снизу и в каждом столбце поднимаетесь вверх. (3) Вы берете столбцы снова в том же порядке, но проходите каждый столбец дважды, сначала вниз, а затем вверх; когда, спускаясь, вы достигаете последнего числа, вы записываете результат, а, поднимаясь, вы его контролируете. (4) Сложите сначала 1-е, 3-е, 5-е, … числа, затем 2-е, 4-е, 6-е, … числа и, наконец, две полученные суммы; это требует некоторых дополнительных записей. (5) Проделайте сложение один раз руками и один раз машиной и т. д.

11. 59.

12. 10 ^{– 9}. (Не 10 ^{– 3} или 10 ^{– 7}.)

Нет решения: 1, 7, 8, 9, 13.

БИБЛИОГРАФИЯ

I. КЛАССИКИ

Евклид, Начала Евклида, т. 1–3, М.–Л., 1948–1950. Указание: «Евклид III, 7» отсылает к предложению 7 книги III Начал.

Descartes, Oeuvres, edited by Ch. Adam and P. Tannery. Особый интерес представляет работа «Правила для руководства ума», см. Рене Декарт, Избранные произведения, М., 1950.

Euler, Opera Omnia, edited by the «Societas scientiarum naturalium Helvetica».

Laplace, Oeuvres complètes. Особый интерес представляет «Опыт философии теории вероятностей», М., 1908.

II. НЕСКОЛЬКО КНИГ СО СХОДНОЙ ТЕНДЕНЦИЕЙ[168]

Курант Р., Роббинс Г., Что такое математика?, М., 1947.

Радемахер Г., Теплиц О., Числа и фигуры, М., 1966.

Toeplitz O., Die Entwicklung der Infinitesimalrechnung; эта книга представляет особый интерес.

III. ОТНОСЯЩИЕСЯ К ЭТОЙ ТЕМЕ БОЛЕЕ РАННИЕ РАБОТЫ АВТОРА

Книги

1. Задачи и теоремы из анализа, М., 1956, тт. 1–2 (совместно с Г. Сеге).

2. Как решать задачу, 2-е изд. М., 1961[292]. (См. также Д. Пойа. Математическое открытие, М., 1970. — Прим. перев.)[169]

3. Wahrscheinlichkeitsrechnung, Fehlerausgleichung, Statistik. В книге Abderhalden's Handbuch der biologischen Arbeitsmethoden, Abt. V, Teil 2, S. 669—758.

Статьи

Geometrische Darstellung einer Gedankenkette, Schweizerische Pädagogische Zeitschrift, 1919, 11.

Wie sucht man die Lösung mathematischer Aufgaben?, Zeitschrift für math, und naturwiss. Unterricht., 63 (1932), 159–169.

Wie sucht man die Lösung mathematischer Aufgaben?, Ada Psychologica, 4 (1938), 113–170.

Heuristic reasoning and the theory of probability, Amer. Math. Monthly, 48 (1941), 450–465.

On Patterns of Plausible Inference, Courant Annivers. Vol., 1948, p. 277–288.

Generalization, Spezialization, Analogy, Amer. Math. Monthly, 55 (1948), 241–243.

Preliminary remarks[293] on a logic of plausible inference, Dial., 3 (1949), 28–35.

With, or without motivation?, Amer. Math. Monthly, 56 (1949), 684–691.

Let us teach guessing, Études de Philosophie des Sciences, en hommage à Ferdinand Gonseth, 1950, p. 147–154. Éditions du Griffon, Neuchâtel, Suisse.

On plausible reasoning, Proc. Intern. Congr. of Math. 1950, v. 1, p. 739–747.

Джордж Пойа[294]

МАТЕМАТИКА И ПРАВДОПОДОБНЫЕ РАССУЖДЕНИЯ

М., 1975 г., 464 стр. с илл.

Редакторы. Е. Д. Соломенцев, Ф. И. Кизнер

Техн. редактор А. П. Колесникова

Корректор Е. Я. Строева

Сдано в набор 29/XII 1974 г.

Подписано к печати 18/IV 1975 г.

Бумака 60 × 90¹/₁₆, тип. № 3.

Физ. печ. л. 29. Условн. печ. л. 29. Уч.-изд. л. 33, 32.

Тираж 100 000 экз. Цена книги 1 р. 71 к.

Заказ № 1807.

Издательство «Наука»

Главная редакция физико-математической литературы

117071. Москва, В-71, Ленинский проспект, 15

Ордена Трудового Красного Знамени Ленинградское производственно-техническое объединение «Печатный Двор» имени А. М. Горького Союзполиграфпрома при Государственном комитете Совета Министров СССР по делам издательств, полиграфии и книжной торговли. 197136, Ленинград, П-136, Гатчинская ул., 26.

---

[1] Нумерация сверху страницы. Примечания и комментарии публикатора электронной версии имеют форматирование, как здесь, в отличие от сносок в самой книге. Что касается «родных» сносок, у них обычное форматирование. Единственное различие: книге сноски на каждой странице нумеруются с единицы. В электронной версии — нумерация сквозная. Что касается самих комментариев и примечаний публикатора электронной версии, они имеют сугубо личный характер — вроде пометок на полях — и ни в коем случае не предлагаются читателю книги, если последнего они раздражают своей навязчивостью или дилетантизмом. Попадались же нам в жизни такие бумажные книги. Да, тоже эти маргиналии могли вызывать определенное раздражение читателя. Но иногда, как пушкинской Татьяне, они помогали справляться с какими-то жизненными проблемами. Впрочем, хоть и немного в процентном отношении, среди примечаний публикатора есть также справочные сведения, которые он внес для себя, но они могут пригодиться и читателю. А что-то может и позабавить читателя, когда он немного отупеет от математичности читаемого. В частности, театральные приложения ряда мест в книге.

[2] В первых публикациях автора на русском языке именно так транскрибировалась его фамилия. Разумеется, когда приводятся выходные данные этих изданий, это написание сохраняется.

[3] К сожалению, доступным оказалось только первое издание.

[4] А в художественном творчестве (в первую голову — в тетре, где все кроме актера — иллюзия) на иллюзиях строится все. Впрочем, как верно отметил Михалыч, наша современная жизнь столь иллюзорна, что мы, словно Дон Кихот, ощущаем себя в реальном мире только убегая в мир фантазий, и два часа в зрительном зале оказываются «посещением» реальной жизни сравнительно с той, которая ждет нас за стенами театра.

[5] По гиперссылке на номерах заданий можно переходить к соответствующим ответам и решениям.

[6] Знаковой!

[7] Думается, высоты всех четырех вершин также пересекаются в центре вписанного шара. Такова структура «Король умирает»: в центре — Король, вершины, соответственно, заняты Марией, Доктором, Жюльеттой и Стражем. Как минимум одна из ячеек этой структуры имеет парадигматична: Мария когда-то заместила Маргарет. То есть первая —in praesentia, вторая — in abcentia, но обе — королевы. Таким образом, структура оказывается не столь жесткой, как представляется нам традиционный тетраэдр. В двойной вершине гнездится деструкция.

[8] Опять автор одушевляет неодушевленные объекты. Или это он так шутит?

[9] [Примечание к примечанию] Понятно, почему так искажена фамилия автора. Она была искажена в издании, на которое идет ссылка, а при ссылке нужно указывать издание так, как оно напечатано.

[10] Здесь возникает аллюзия с михалычевым условием игры: ставка в игре должна быть максимальной, предпочтительно, когда на кону жизнь игрока. Чем выше ставка, тем выше ценность игры, тем выше выигрыш, выше удовлетворение от игры.

[11] Разное управление издатели применили из-за последних чисел (12 и 3). Мне кажется это неверным, поскольку объектом управления и во втором случае должен быть не один из сомножителей, а — произведение, то есть — как в первом случае — множественное число.

[12] Воображение оказалось одушевленным.

[13] Сомнительный совет, по крайней мере если говорить о творческом процессе;например, — об анализе роли. Поэтому крайне важно проследить, окажется ли в этом совете толика рационального, ведь тогда можно будет сделать какие-то выводы и насчет творческой деятельности. Ведь то, что внутренняя, душевная работа что у нас, что у соседей, имеет общую природу и структуру, никто не отменял.

[14] Возможно, здесь есть связь (аналогия!) с «способами репетирования» Мачо. Каждый из этих способов решает целый комплекс задач: держать, притягивать, устремляться, сливаться. И сперва мы решаем их по отдельности, затем комбинируем по две, по три и лишь потом добиваемся полного синтеза в овладении данным инструментом техники актера.

[15] В искусстве же любой намек на закономерность — художественный факт. Как в случае со вторым столбцом: едва наметившаяся связь с двойкой немедленно становится доказанной для зрителя (читателя и т. д.). и как только появляется внесистемня пятнашка, это становится новым важным художественным фактом. Если в реальной действительности «после того — значит вследствие того» — глупость, то в художественном произведении — это непреложность.

[16] Так в книжке: ни то ни се. Ни «двух новый частей» (одушевленное), ни «две новые части» (неодушевленное, так правильно).

[17] Как я пытаюсь высмотреть параллелизм с художественным мышлением при, скажем, анализе пьесы или роли.

[18] Как я спросил себя, когда Нина Заречная заявила, что она уже два года не плакала: а когда же она плакала два года назад. И тут же обнаружил ответ прямо в тексте пьесы. А следом — обнаружил и характер персонажа, который плачит, когда счастлив и ни одной слезинки не роняет в несчастье.

[19] …и художника!

[20] Но натуралист Бор утверждал: «Главное — чтобы работало».

[21] Что мы можем наблюдать на примере чернобыльской аварии. Вероятность совпадения случившихся события была, можно сказать нулевой, но это невероятное совпадение произошло.

[22] Это типа олимпийские кольца? Или эмблема ауди?

[23] Например, Михалыч в одном месте заявляет, что «метод действенного анализа» и «этюдный метод» — одно и то же, в другом — что «был период, когда он считал, что это одно и то же». А истина никому не известна. И это при том, что эти понятия — важнейшие в театральной репетиционной практике и ими пользуются все кому не лень.

[24] В книге именно так.

[25] А режиссер рассматривает персонажей и классифицирует их по самым различным, желательно наиболее неожиданным и парадоксальным признакам, начиная от возраста и пола, социального статуса и семейного положения — до темперамента и психического здоровья. И оказывается, например, что Нина Заречная — это один из возможных сценариев юности Аркадиной, а Аркадина — один из сценариев будущего Нины. Полина Андреевна — еще один возможный сценарий женской судьбы. Плюс еще и Маша — все они существуют не только синтагматически на тех местах, по которым их расставил драматург, они еще представляют собой парадигматическое множество, вполне возможное в плане взаимозамены в любой конфигурации. То же можно сказать про Тригорина и Треплева, Сорина и Дорна и даже — Шамраева и Якова. Сегодня Шамраев командует Яковом. Но не пройдет и двадцати лет — и Яков будет ставить Шамраева к стенке и расстреливать из своего боевого маузера.

[26] Видимо опечатка — вместо «Он».

[27] Здесь, видимо, должна стоять открывающая кавычка.

[28] По-моему, здесь нужно было либо выделить «может» запятыми, тогда уместно будущее время совершенного вида «удастся». Либо это должен быть инфинитив «удасться», тогда никаких запятых не нужно. Просто это различные предложения с точки зрения грамматики, хотя по существу мысли значительного нюанса нет.

[29] Похожая ситуация возникала, когда студент-режиссер Шура Лебединский допытывался у профессоров точного ответа, как воплощать через актера свой анализ драматического материала. Педагоги же только отшучивались, мол, всеми доступными вам как режиссеру средствами. Сегодня я понимаю, что ответ был не совсем шутливым, в нем было много точного, поскольку нельзя алгеброй гармонию поверить. Ну а Шура до сих пор сперва придумывает спектакль, а потом встраивает в него актера. И спектакль, рожденный в голове режиссера, а не бережно взращенный вместе с актерами, оказывается порою даже блестящим, но всегда — холодным.

[30] А вот в игре ее участником постоянно приходится именно этим заниматься: рассчитывать вероятность и везение, чтобы, исходя из именно этого расчета строить дальнейшую игру, выбирать очередной ход или комбинацию.

[31] Это уже «Сирано де Бержерак»…

[32] В книге именно так — большая буква после запятой.

[33] А я его оттуда тупо скопировал сюда.

[34] Похоже, опечатка, уместней сказать «Так,…».

[35] Опечатка.

[36] Или степенном ряду…

[37] Не понял, «проводящая» или «производящая»? Это оговорка-описка-опечатка или Дъердь ввел термин, уподобляясь Лапласу?

[38] Наверное, можно все многоугольники кроме треугольников аналогизировать со сложными, или «составными» числами. Ведь только треугольник невозможно разбить на два линией, проходящей через вершины. То есть в планиметрии существует только одно-единственное «простое число»? Или величина углов — дополнительные его качества, определяющие бесконечное множество этих «простых чисел?». А как будет жить эта аналогия с вводом 3-го измерения? Тут уже мое воображение не срабатывает. Что уж говорить о высших измерениях…

[39] Что значит, не было у Дьердя компьютера! И, например, программки Excel.

[40] То есть — данный член оставшейся последовательности (2-я строка) и все предыдущие (находящиеся слева от этого члена). Например, 9² = 1+3+5+7+9 = 25.

[41] Темное место. Похоже, после последней скобки точка лишняя. Тогда какой-то смысл появляется.

[42] Не знаю, что означают эти игры с регистром, но в книге именно так.

[43] В художественном творчестве доказательство очевидного почти не обязательно. Ведь исключения из выведенных правил не грозят ничьей жизни и здоровью. Поэтому, как правило, интуитивная уверенность художника в своей правоте оказывается достаточной, чтобы в нее поверить, Последнего же вполне достаточно, чтобы заразить адресата своего творчества. «Если вы действительно растроганы, искренность ваших чувств передастся другим» (Камиль Коро). «Жест, на кого-то направленный, зов куда-то призывающий, зрителем дорисовывается, ему мерещится сам живой повод к жесту и к зову независимо от того, был он или не был взаправду» (Н. Я. Берковский).

[44] Иногда возникает ощущение, что Пойа сам переводил книжку на русский. «Растояние точки от…»

[45] Противоречие есть. И состоит оно в возникающем серьезном подозрении, что предыдущей фразе, после «12», должна стоять запятая и что, соответственно, предлагается применить решение нового, 29-го, номера к старому, 12-му. А вовсе не то, что 29-й номер уже возникал в 12-м, как можно понять фразу в отсутствие этой запятой.

[46] Обращено, надо понимать, к тем, кто и ученые книжки читает, открывая каждый раз наобум, чтобы загадать желание.

[47] Возникает, судя по всему правильное, ощущение, что автор просто собрал фигуры с наименьшими площадями поверхностями (наименьшими периметрами), превратил это их качество в «условие» и на этом уже выстроил задачи. В целом же речь идет о том, что «правильности» фигуры (в чем бы то ни было) неизбежным и необходимым (а возможно, и достаточным) образом сопутствует минимальность или максимальность какого-то из параметров фигуры.

[48] Налицо аналогия, связанная с теорией пределов. Если число углов «основания» фигуры (правильного многоугольника) устремить к ∞, очевидно, что получится фигура вращения (вспомним вычисление Архимедом площади сферы в 1-й книжке). Уверенность, основанная на многочисленных аналогиях, здесь настолько же велика, как и уверенность Эйлера в своей формуле. Другими словами, если этот факт вдруг понадобится исследователю как промежуточная, вспомогательная теорема, его сильнейшим образом будет привлекать возможность использовать его не доказывая, чтобы не терять на это время и пыл, а сосредоточиться на главной своей цели. Единственное, что можно еще заметить, что если в художественном творчестве такое «выпадение» из звена рассуждений не только допустимо, но, пожалуй, даже приветствуется (закопаешься в частностях — потеряешь «тепло» главной цели), то в научном исследовании все равно рано или поздно необходимо вернуться к этому месту и провести доказательство, как бы ни лень было этим заниматься.

[49] Сводя все к простейшему случаю (специализации, что ли, уже не помню терминологию), а именно — двойному тетраэдру, мы получим ¹/₆ часть. Так и подмывает обобщить, а затем доказать. Интересно, угадал я или нет? Единственно, я не понял, зачем нужен объем? Чтобы исключить его отсутствие (высота равна 0)?

[50] Ах вот причем тут объем — это просто константа.

[51] Причем подозреваю, что боковые грани этой пирамиды представляют собой равносторонние треугольники. И тогда поверхность каждой из них составит, соответственно (если поверхность обозначить как S), ³/₁₆·S. Не знаю, дает ли это что-нибудь. Так, поупражнялся от нефига делать…

[52] Ну, здесь уж кто бы сомневался. Как из треугольника мы по аналогии переходим к пирамиде (а значит, в частности, к тетраэдру), так от пирамиды — к конусу. Соответственно, и подобные свойства будут одинаковыми.

[53] Неужели ¹/₄?

[54] Ну как чего? Треугольной призмы, в основании которой — равнобедренный прямоугольный треугольник, а высота (призмы!) — в два раза меньше длины каждого из катетов основания.

[55] Распознавалка дала «код», что тоже, похоже, имеет место во всем данном рассуждении.

[56] То же самое происходит с брошенным с высоты предметом, например, с плотницким отвесом: груз, по сути, — падающий предмет, а шнур обозначает пройденную грузом траекторию, которая и оказывается кратчайшим расстоянием между пунктом начало движения и его окончания (ввиду возникновения препятствия).

[57] Подобно тому как в буквально художественном творчестве именно из различных сопротивопоставлений, когда выявляется сходное в различном и различие в сходном, и извлекается эстетический эффект.

[58] Вправо.

[59] Катится, конечно, не точка, а окружность.

[60] Как и художественное произведение.

[61] Между прочим, давным-давно в какой-то книжке, кажется, посвященной Карлу Марксу и математике, мне уже встречалась эта тема. Как раз, кажется, история касалась описанной в другой книжке нашего автора методики нахождения параметров фигур вращения (кажется, именно площади поверхности сферы), использовавшейся Архимедом. Там еще говорилось, что рукописи, в которых описывались вычисления греческого математика, были обнаружены совсем недавно, в XX в. Впрочем, похоже, именно об этом речь пойдет в этой книге.

[62] Ага, значит, все-таки новый материал сравнительно с другой книгой: там речь шла, как я уже сказал выше, о площади поверхности сферы. Близко, но другое.

[63] Огрех переводчика. Ясно, что автор не противопоставляет факты, а, напротив, сопоставляет их. Поэтому, скорее надо было здесь переводить не «однако», а «в то же время» или как-нибудь в этом духе.

[64] То есть биссектрисы угла координат.

[65] Квадратные диски? Интересно, как там было у автора.

[66] Очередной раз закрадывается подозрение, что Дьердь сам переводил себя на русский.

[67] Вот так: что хотим — склонят, что нет — не хо́чу.

[68] А тут вариантов-то? Где можно — вброд, а так — в ковчеге.

[69] Не так глубоко, как надо? Не хватает глубины?

[70] В итальянском, вроде, двойное «t».

[71] Наверное, все-таки, Рейли. Чувствуется год издания, тогда еще писалось Джерсей, Виверлей, Ануйль и т. п. После изысканий выяснилось, что он вообще Джон Уильям Стретт. Но, кстати, в качестве лорда его чаще называют таки да Рэлеем.

[72] Ошибка с родом подлежащего: либо здесь, либо в предыдущем предложении — либо «математик» там, либо «она» здесь.

[73] Обять переводчик задумался по-татарски.

[74] Видимо, в значении «горячо».

[75] Тех, кто что-нибудь понял, поздравляю. Прямо как у Зиновьева. Курсант Ибанов дал по морде курсанту Ибанову, о чем тут же курсант Ибанов настучал замполиту курсанту Ибанову.

[76] Интересно бы узнать, что означает это слово. ОРФО не подчеркивает. И чем симметрический отличается от симметричного. Посмотрел в Сетке. Большинство словарей говорят о синонимии.

[77] Когда возникает вопрос, почему у меня в «Чайке» одни сцены играются на русском, другие — на французском, поначалу я не мог объяснить это иначе как фоном. Еще когда я задумывал этот спектакль, важной задачей для меня было оправдать (для себя и зрителя), зачем русским актерам играть русского автора на французском. Отсюда невольно возникло побуждение как-то, контрабандой, может, частично, но вернуть пьесе родной язык. В этих интуитивных поисках подвернулся повод: «Между третьим и четвертым актом проходит два года». То есть пьеса написана в двух временах, есть два различных хронотопа, которые я как постановщик должен как-то маркировать. (Конечно, тогда я не думал в подобных терминах.) И куда как проще совершить эту маркировку: один хронотоп помечается одним (естественным) языком, другой — другим. Могу гордиться, что я не полностью поддался этой чисто служебной задаче чтобы облегчить себе работу: у меня ни секунды не возникло тогда мысли дать бо́льший объем текста (первые три акта) на русском и только четвертый — на французском. Скорее всего, потому, что уже тогда я склонялся к тому, что первые три акта — прошлое (искаженное, воспоминаниями, виртуальная реальность, существующая лишь в памяти — чьей-то; наиболее вероятно, в памяти Кости Треплева) по отношению к 4-му, протекающему спустя два года, а не 4 — будущее по отношению к 1—3-му, разворачивающимся за два года до 4-го. Так «возросла моя уверенность в моей догадке». А когда я стал обдумывать, как я буду нарушать получившуюся схематическую идею (нарушение схемы — обязательная часть творческого замысла, о чем многие режиссеры часто забывают, а то даже и не догадываются об этой важнейшей составной части своей работы), сразу, разумеется, во всей своей несомненности появилось решение посреди франкоязычного 1-го акта отдельные реплики (в основном апарты) давать на русском. Соответственно, когда среди русской речи начинала звучать (уже не обязательно апартом) французская речь… возникло мощнейшее подтверждение избранного пути. Ведь так оно и было в дореволюционной России: сплошь и рядом звучала французская речь, что никого не удивляло. Отсюда — естественным образом спектакль Треплева зазвучал по-русски, спектакль, во время которого Аркадина, Треплев, Полина Андреевна вставляют реплики на французском. И в этот момент появилась одна из наиболее подкрепляющих мыслей, переводящих «техническую работу» в разряд идейно-художественной концепции: чеховские персонажи неспособны понять друг друга: они говорят на разных языках. Именно в этот момент моя уверенность в правильности выбора превратилась в убежденность и уже никакие контраргументы не могли меня сбить с намеченного пути. И все последующие уточнения, даже самые удачные (в «русскоязычном» финале Нина произносит тот же монолог по-французски: теперь уже Костя и Нина разделены стеной непонимания, и — как материализация этого факта — занавес, который закрывается, отделяя героев друг от друга теперь уже необратимо, навсегда) не имели уже никакого значения: ни положительного, ни негативного.

[78] Или же полное крушение всех столь кропотливо выстроенных эвристических и индуктивных конструкций. Впрочем, в художественном творчестве подобная ситуация почти невозможно: всегда можно смухлевать и проигнорировать неочевидное противоречие: общая убедительность всего прочего сводит это противоречие практически к нулю, оставляя пищу лишь самым тонким и придирчивым критикам.

[79] Наверное, я тоже исключительный. Потому что мне в школе и в институте не раз и не два попадались задачи, которые были нерешаемы именно по этой причине, хотя внешне условия давали все необходимое и достаточное для нахождения решения. И лишь после бесплодных попыток выяснялось, что эта достаточность иллюзорна, поскольку одно из составленных уравнений дублирует остальные (как это показано выше: 0 = 0).

[80] Кстати, ни в школе, ни в институте нас не учили этому. Нам прививали самые общие и готовые законы, теоремы, формулы и доказательства. А что такое метод математической индукции — в памяти, кроме названия самой темы в виде дежавю, глубокий вакуум.

[81] Еще один стилистический шедевр. Расстояние бывает до, а от — удаленность.

[82] И к анализу драматического материала. Я, кажется уже отмечал вслед за автором: самый продуктивный путь к резульату — непрямой. Быстро найденная сцена показывает только как ее нужно играть, но в этом исполнении нет того, как ее играть не нужно, в ней остутствуют невыбранные варианты, которые обязаны присутствовать in abcentia в художественном результате.

[83] И, вообще говоря, по-видимому, от этого и случаются чернобыли и гибель ВТЦ.

[84] В каком смысле? Слишком? Или резонно?

[85] Мне кажется, сегодня было бы правильнее сохранить слово «паттерн», поскольку оно уже активно вошло в русский язык в своем первородном звучании. Более того, слово «схема» не сохраняет нюанса патерна — повторяемости, типичности, узнаваемости подловленной, замеченной в жизни, схемы.

[86] Естественно, в наше время можно было бы продолжить вычисление с помощью компьетеров, наподобие многолетнего и ныне уже завершенного вычисления генома. Но какая, в отличие от последнего, от этого практическая польза?

[87] Так возникло прецедентное право, рассадник судебных ошибок.

[88] Паттерн, не забывайте! Кстати, словарь дает «образец, шаблон, система». Кстати, последнее (система) вполне передает значение «общая схема».

[89] Плеоназм, господа переводчики!

[90] Опечатка в книге.

[91] Так одушевленных? Или, все-таки, оси?

[92] Это точно не по-русски. По-моему, в этом смысле можно сказать «относительно правдоподобно».

[93] Совершенно — можно сказать. Но не очень!

[94] С помощью линейки и циркуля невозможно. Но мне нравится решение Леонардо. Берем цилиндр высотой в половину радиуса основания. И прокатываем его по плоскости, отметив начало и завершение полного оборота. Получаем развертку боковой поверхности этого цилиндра. Ее площадь: 2πr × r/2 = πr² оказывается, как видим, равна площади круга (основания цилиндра). А дальше дело техники: площадь прямоугольника равна произведению его сторон: ab. А вот как дальше — не могу сообразить. Наверное, надо извлечь из ab квадратный корень. Сторона квадратуры круга — c = √͞a͞b. Вроде, так…

[95] В книжке сделано две выноски на один и тот же текст: на строчку за одну да этой и на текущую. Я просто сделал две ссылки на два идентичных текста.

[96] В книге — три одинаковых знака выноски, отсылающие к одной и той же сноске.

[97] Это очень похоже на упражнения Мачо на развитие воображениях: следить в своем воображении, как происходят превращения гребешка в лес, зеркальца в море, старушки в красавицу, а последней — в лягушку и т. п.

[98] В ссылке речь идет о 95-й ссылке (согласно «сквозной» нумерации данного электронного документа) на с. 248. эта ссылка вновь дублируется, в данном случае отсылок к одному и тому же тексту в этой таблице 5.

[99] Ну, скорее, объединены скобкой.

[100] Напрашивается ревность — и фонологически, и по числу букв. Хотя ревность на самом деле никак не предполагает верности, напротив, выглядит правдоподобным предположение, что наиболее ревнивы как раз люди полигамного типа: стремление к личной свободе у них вполне может сочетаться с уязвимым самолюбием и собственничеством.

[101] Во! А я дурак уже стал оспаривать тот смысл, который автор кроссворда и не вкладывал. Я думал, что «форма» относится к означаемому, а оказалось — к означающему, то есть, берем слово «верность», меняем его внешнюю форму и получаем… впрочем, само слово я, видимо, угадал.

[102] Это, наверное, первый взнос? Или подержанная тачка?

[103] В книжке были использованы две стрелки одна над другой: , но я такого символа не нашел ни в таблице, ни в эквейшне.

[104] Кто? Предположение? Доказательства? Оба двое?

[105] То есть по любому.

[106] Чем бы заменить? Наверное, более по-русски: «основательным». «Вероятным», в конце концов.

[107] Кто «она»? Ось? Ситуация? А-а! Последовательность!

[108] Так я для себя сформулировал самочувствие художника: с одной стороны представлять себя равным Богу. Ведь художник, так же как последний в свое время, сотворяет художественный мир своего произведения. С другой стороны полезно позиционировать себя пророком: не ты творишь, а Некто творит через тебя. Особенно четко это ощущаешь по завершении работы, когда спектакль ведет себя совершенно самостоятельно от тебя, самым непредсказуемым образом. И, конечно, для меня, атеиста, это все звучит тоже как «шутливая аналогия». Но тем не менее помогает, работает.

[109] Точно по Мачо!

[110] Да? Оно делится на два?.. В общем-то да, причем без остатка!

[111] Надо же, какой архаизм! Тогда еще не было орла и решки? Или академический редактор решил, что это слишком легковесная лексика?

[112] В книжке — удовлетворящую.

[113] Французское словосочетание, означающее смысл, смысл существования, разумное основание существования. (Википедия)

[114] Это еще один Сеге? Соавтор Дьердя-Джорджа был, вроде, Габор. Неужели это мадьярская форма имени Петр? Петер, сколько я понимаю, — немецкая, они ж публиковались в Германии.

[115] Не знаю, что означает эта единица, но в книжке напечатано именно так.

[116] Еще бы вспомнить, что это за зверь такой…

[117] И очень важно умение не уставать от неудач и продолжать выдвигать такие зыбкие, шаткие, по аналогии с имеющимся опытом казалось бы даже не стоящие взгляда предположения. Иначе в последующем творчестве можно начать пропускать наиболее ценные и таким образом его, это творчество постепенно обеднять и утеривать, что и происходит, как мы видим, с успехом со множеством талантливых людей, скудеющих духом с годами.

[118] Я подумал, что вероятность и правдоподобие — это та самая ткань, из которой строится искусство. Я даже не про правдоподобие чувств. Даже если говорить об истинности страстей — это же лишь страсти, всего лишь страсти, которые могут реализоваться, могут сублимироваться и видоизменяться, они не являются ясной и определенной реальностью. Даже они — то чуть ли не единственное матерьялистически истинное, что у нас имеется в распоряжении.

[119] И в настоящее время, на фоне техногенных аварий типа чернобыльской или лос-родеоской, а также массовых судебных ошибок на основе косвенных доказательств (то есть основанных на высокой вероятности) — потерпела практически полное фиаско. Не говоря уже о все растущем числе «невероятных» фактов, вызывающих предположение о высокой вероятности невероятного. Думаю, даже если не говорить об открытиях, связанных с паранормальными явлениями, космическими и физическими аномалиями, достаточно обратиться к известному каждому человеку, накопившему определенный жизненный опыт, аномально высокому количеству совпадений, возникающих в нашей жизни, что никакая теория вероятностей объяснить не способна. Хотя, с другой стороны, это так же субъективно, как и соотношение опубликованных/неопубликованных научных предположений, о которых говорилось в конце предыдущей главы. Несовпадения мы для себя не отмечаем, именно совпадения привлекают наше внимание, так что статистику здесь поймать крайне сложно.

[120] Что-то это мне напоминает о роли личности в истории…

[121] Так вот почему они так часто ошибаются!

[122] Это напоминает историю с разложением на множители из предыдущей главы: в пределе четное и нечетное равны, а так — нечетных меньше.

[123] Точно здесь о роли личности в истории. Главной ошибкой марксизма как раз считается рассмотрение исключительно результатов массовых явлений без учета случайностей, связанных с каждой конкретной личностью.

[124] Как у стоппардовских Р и Г.

[125] Вдруг подумалось: а как же те, кто не попал под статистику? Родившиеся в трущобах и резервациях? И, наоборот, в комфортабельных клиниках? Может, у индейцев только покахонтос рождаются? Или у пуэрториканцев — только мучачос?

[126] Масло масляное. Иррегулярность и есть непредсказуемость.

[127] И как раз в этот-то момент и наступает чернобыль.

[128] Но не обязательно!

[129] Прямо «Жмурки» свежепреставившегося Октябриныча. «С помощью вот этого простого устройства…»

[130] А это уже снукер.

[131] Нет, не снукер. Красные шары ведь тоже выставляются.

[132] Так в книжке; опечатка.

[133] Те самые исключение, подтверждающие правила, из-за которых тогда взбесился Лана.

[134] Чем-то напоминает игру про дилемму заключенного.

[135] Ага! А я было подумал, что редактор решил, что этот оборот всегда выделяется запятыми…

[136] Действительно вряд ли. Но для шара номер 1 фишка 1 явно привлекательнее, чем фишка 2!

[137] По правилам грамматики «независимыми» здесь следует писать в два слова. Но по правилам науки — здесь вводится термин, который нужно писать в одно слово.

[138] Вот именно! Не потому, что мы о нем знаем, а потому, что он не вызывает абсолютного доверия.

[139] И астрологи — тоже. Ведь до совсем не так уж давнего времени их и не различали. Если не ошибаюсь, и Коперник, и Ньютон были также и астрологами.

[140] И, увидев в этом месте знак выноски, я понял, что наши редактора, крестясь и перестраховываясь, станут обвинять автора в агностицизме. И впрямь, перечитайте ту марксистскую чушь, которую они там понаписали! Вся магистральная мысль автора, весь пафос книги утверждает недоступность абсолютной истины, но именно в этой недоступности и кроется неудержимая устремленность к ее постижению. Вновь и вновь утверждается путь как цель, а достижение цели, конец этого пути — как утеря самой цели.

[141] И принимаем.

[142] Может, здесь и зарыта собака? Какие-то вероятности (наступления чернобыльских события, к примеру) — не первичные данные, а — вычисленные на основе других вероятностей, также вычисленных на основе каких-то еще и т. д. При этом, возможно, не учитывалась девиация, возникающая и неизвестным образом влияющая на результат в зависимости от снижения первичности промежуточных вероятностных результатов.

[143] Обязательно нужно попытаться разработать театральное приложение.

[144] И наебать казино.

[145] «Вполне благоприятным», — сказал бы русский человек. Но не русский переводчик-математик.

[146] Класс! Как часто мы упускаем из виду эти практические «пылинки» и «раздавленные бабочки», а потом удивляемся, почему теория не состыкуется с практикой. Пример — вышеупомянутое игнорирование марксизмом (а особенно ленинизмом) индивидуальной личности.

[147] Блин, до меня наконец доперло. Честной кости быть не может, поскольку сами метки на гранях вносят искажение: у шести точек масса ровно в шесть раз больше, чем у одной! И при бесконечном увеличении выкидывания этой кости эта разница начинает играть все большую и большую роль.

[148] С винцом?

[149] Наверное, все-таки, «статистические». Или вообще «этих», но тогда совсем по-китайски получится.

[150] Или «гипотез»?..

[151] Наверное, «рождения». Иначе тоже будет по-канарски: «трех». Пейте соков натуральных.

[152] Как видим, на черно-белой иллюстрации розовые и белые выглядят одинаково, так что различить их возможно только исходя из логики схемы, в частности, — из числовых данных.

[153] Очередной переводчицкий ляп. Классификационный порядок называется розоцветные (калька с вышедшего в настоящее время из употребления латинского Rosiflorae), то есть растения, строение цветков у которых такое же, как у роз.

[154] Интересно, как бы он выразился, если бы узнал подробности чернобыльской аварии.

[155] Кошмар! Терминология терминологией, но нельзя же так обращаться с русским языком!

[156] Интересно, куда делся один случай?

[157] Ну, то есть, функция P от аргументов E и H.

[158] Очень трудно понять при таком изложении, о чем идет речь. То есть, при оценке вероятности мы учитываем событие E.

[159] Наверное, бикфордов шнур?

[160] Почти буквально в одну кучу свалены и гвозди, и бублики.

[161] Кто бы говорил. Интернет-искалка выдала «Пойа» чуть больше 60 000 (причем столь высокий результат, думается, главным образом обязан автору этой книги), а «Моргенштерн» — свыше десяти миллионов. Утренняя звезда (как переводится эта фамилия) — Венера. Ну а чем не фамилия Венеров или Венерский?

[162] Была такая манерка одно время Ануй был Ануйль, Райпай — Распайль. Вспомним лорда Рэлея, которого так переводят чаще, чем как Рэйли. Может, чтобы отличать от знаменитого шпиона, заманенного и замоченного чекистами (сериал «Операция ”Трест“»)?

[163] Теперь номер стал одушевленным.

[164] Может, я не на ту карту наткнулся, может, не разобрался, но у меня впечатление что там номера более 200. Впрочем я видел, как в Сетке «крышку» сирконфлекс называют циркумфлексом.

[165] Тоже из оперы Распайль. Хвостик внизу буквы (например, ç) называется «седий».

[166] Хотелось бы знать, какой из современных языков имеется в виду? Нидерландский? Я на всякий случай выбрал его нидерландский вариант (в отличие от бельгийского). Спеллчекер, вроде не подчеркивает ничего.

[167] Для меня полная загадка эти отдельные курсивные «о», но так было в книжке. Может, в наборной кассе они лежали вперемешку, вот наборщики и втыкали те, что под руку попадались.

[168] А здесь подчеркнул именно из-за отсутствующего умлаута в букве «ü».

[169] Странно, мне казалось, что лексика польского очень славянская и часто просто можно понять, зная только русский, польский текст. То есть, польский должен быть столь же далек от английского, как и русский. С другой стороны, венгерский — это вообще какой-то типа финского, то есть столь же далек от английского, как и от русского.

[170] Нет, это были подмешаны курсивные «о» в кассу. Потому что здесь, в заголовки делать отдельные буквы курсивом, согласитесь, совсем ни к чему.

[171] И выглядит тупиковой.

[172] Опять одушевленное неодушевленное.

[173] Видимо r — от rain, а s — от sun.

[174] Надеюсь, что все знаки верные, тогда последний оборот — расшифровка предшествовавшего выражения (окончательная устойчивая относительная частота).

[175] В книжке — в два слова. Формально, ошибкой не является. Но, исходя из контекста, излишне, поскольку в данном случае очевидна замена — «часты».

[176] Здесь как раз не совсем ясный юмор: почему не 51-й? С другой стороны, если считать Гавайи и не имеющие статус штата территории США вроде Пуэрто-Рико, то там можно насчитать до 60 административно-территориальных единиц

[177] Ну нельзя так говорить, даже если это терминология! Невероятно, оно и есть невероятно без каких либо степеней. Это как хвост Иа-Иа — он либо есть, либо нет — тут нельзя ошибиться. Либо вероятно, либо — невероятно.

[178] Дьердь, видимо, привыкнул меня искать аналогии. Моя — разная режиссерская практика. Один режиссер (напр. Шура) придумывает спектакль во всех подробностях идейно-художественного содержания, причем автор, актер и зритель для режиссера второстепенны. Зато обязательно гармонично задуманы общая композиция, партитуры атмосферы, темпоритма, мизансцены. Автор для режиссера — только повод для собственного авторского творчества, актеров он встраивает в уже готовый в его воображении спектакль, поскольку для них уже подготовлены соответствующие «гнезда». Ну а зритель вообще такому режиссеру не обязателен и хотя бы факультативен. Другой режиссер (я стремлюсь быть таким) чутко прислушивается к автору, пытаясь угадать, в какую композицию выстраивается спектакль, чтобы голос автора прозвучал внятно, театрально. Вместе с актером он вслушивается в самого актера, в его партнеров, в современность и вместе они терпеливо репетируют, радостно отмечая (как можно позже!) возникновение «тона роли», неожиданных мизансцен, зародышей атмосферы, ритмических стыков. Такой театр рождается сам, и девизом подобной режиссуры можно принять знаменитое «не навреди», принятое среди врачей, поскольку спектакль рождается и развивается как живое существо: сперва — зачатие и пренатальный период: репетиция, затем — уже в послеродовой период, проходя все стадии: от младенчества — до дряхлости и смерти. И долгожительство спектакля определяется здоровым образом его жизни, включая здоровый сон, активное поведение, правильное питание и т. д. Для такого режиссера главные объекты его внимания, главные источники и составные части будущего спектакля: автор, актер и зритель.

[179] Да… несчастное логическое «или» совершенно не соответствует «или» грамматическому. К сожалению, переводчик сплошь и рядом нарушает пунктуацию, связанную с последним. Я обычно без комментариев ставлю или перед запятой, когда вторая часть является сопоставлением с первой частью, точнее, уточнением или другим именованием одного и того же (по примеру двойных названий: «Безумный день, или Женитьба Фигаро»). При противопоставлении запятая (в соответствии с правилами русского языка) опускается, как в обоих приведенных в сноске случаях. Кстати, думается, форма «и/или» — вполне разумна для нехудожественного текста, поскольку весьма четко определяет то самое включающее значение.

[180] Еще один хвост Иа-Иа.

[181] Я бы, все-таки, написал в два слова.

[182] Здесь я уже не выдержал и написал раздельно.

[183] Шутка милая, но у каждой стороны есть и обратная. В результате останутся только свежие.

[184] Наверное, правильнее перевести «обвинительный вердикт». Потому что осуждение — это когда бабки на скамеечке у подъезда с осуждением смотрят на мини-юбку и колготки в крупную сеточку девицы, вылезающей из-за руля навороченного джипа.

[185] И тем вероятнее подстава!

[186] Если человек, получивший деньги, по выходе из банка расплатился одной из полученных купюр за сигареты, вероятность подставы вырастает во много раз: тот, кто подставляет, имеет только информацию о полученной в банке сумме и, зная, что именно столько будет подтверждено в суде документально, заботится, чтобы получающему досталась ровно эта сумма, а чтобы узнать потратил ли «плательщик» что-то из полученной суммы и сколько, нужны большие усилия и риск. Да и пусть обвиняемый сам доказывает свои траты!..

[187] И, таким образом, при обнаружении хоть какого-то факта, колеблющего обвинительный уклон в отношении, например, «плательщика»(отсутствие у него в период от снятия денег со счета до получения денег «получателем», с одной стороны и покупка в это период сигарет), почти неопровержимо доказывает (с точки зрения здравого смысла) подставу.

[188] Так в оригинале — в одно слово. Неграмотно, но вкусно звучит.

[189] Или, как сказали бы французы, ле дёзаля фуа.

[190] А может, не очень любил.

[191] Видимо, правила.

[192] И большинство людей напроя забывают об этой очевидной истине, возможно, единственной, сформулированной еще Сократом: определенно мы знаем только что определенно мы не знаем ничего. Ассоциативно с этой мыслью соприкасается хохма Поля Валери: бог создал все из ничего, и материал все время ощущается.

[193] А вот здесь я бы написал в два слова или выбрал другую формулировку, например, «расходиться во мнении».

[194] А уж в нашей стране полным полно людей, которых к коллегии присяжных вообще нельзя за милю подпускать. Я имею в виду тех, кто искренне убежден, что само нахождение на скамье подсудимых свидетельствует против обвиняемого. Немало и тех, кто просто сочувствует уркам и по умолчанию неприязненно к участникам событий: прокурору, следствию, адвокатуре. Богатые в любом случае вызывают самые неприязненные чувства у значительной части населения. То же относится к чиновникам. И т. д. и т. п.

[195] А как насчет «непредубежденны»? ОРФО не подчеркивает.

[196] По причине близорукости, косоглазия или иного расстройства зрения.

[197] А вот здесь почему-то в два слова. Для стилистического изящества я бы добавил «друг с другом».

[198] И слегка невозможным.

[199] Вот здесь совершенно правильно в два слова.

[200] ОРФО справедливо подчеркивает: в виду последующего «в отношении» должно писаться в два слова. А писать «мы несогласные» нельзя, поскольку речь во фразе идет но о несогласии как качестве двух спорящих, а именно об их несогласии друг с другом, то есть о ситуации, в которой они находятся.

[201] Так, невозможность представить какой-либо довод в пользу объективного существования психологической атмосферы (спектакля, богослужения, музея, митинга и проч. вида проявления этой массовой эмоции) кроме опыта чисто чувственно-эмпирического, интуитивного, «ненаучного», для убежденного «материалиста» являются самым убедительным доказательством идеалистической абсурдности всякого обсуждения этого явления. С другой стороны, артисты, политики и священнослужители на протяжении тысячелетий с успехом пользуются этим антинаучным явлением, достигая вполне материального успеха (один из наиболее убедительных примеров: приход Гитлера к власти). Лучше всего это сформулировал Нильс Бор: «Главное — чтобы работало». Ученый, между прочим, а не поэт или священник.

[202] Друг с другом.

[203] В книжке в два слова.

[204] В книжке в два слова.

[205] Судя по всему, в оригинале — «бэкграунд». В наши дни можно и не переводить, в таком виде слово воспринимается понятнее.

[206] Например, поставить спектакль, ставящий главным образом на атмосферу: мизансцена, темпоритмическая структура, композиция, рельефность характеров — если и не игнорируются, то оказываются второстепенными, подчиняясь партитуре атмосфер и из них рождаясь.

[207] Структурные интересы на первом месте, постановочная «выразительность» смены темпоритма, вычурность мизансцен и т. п. оттесняют атмосферу на задний план, если не игнорируют ее. Зритель отсекается от участия в создании спектакля, в качестве такового ему предлагается уже готовое и почти неизменное.

[208] Причем эта простая дедуктивная мысль, к сожалению, плохо читается из-за самой индуктивной структуры схем.

[209] Точно, «разумный» ответ обычно звучит как-нибудь вроде: «Это же очевидно!». Например, знаменитое «Этого не может быть, так как этого не может быть никогда. Другими словами, чтобы воздвигнуть сооружение, нужен фундамент. В рассуждении подобным фундаментом может быть только аксиома, постулат, то есть нечто, принимаемое бездоказательно (как само собой разумеющееся), а значит — не имеющее на самом деле под собой никаких разумных оснований кроме нашей догадки, гипотезы, интуитивного ощущения.

[210] Чем больше работаешь в театре, тем чаще приходится принимать решения на чистом наитии, начинаешь шарахаться от интеллектуальных схем, боясь спугнуть именно интуитивное угадывание правильного решения.

[211] В том-то и дело, что преимущество в суде все время на стороне либо денег (поддерживающих преступников) либо на стороне обвинения (что работает, понятно, против невинного). И поэтому оправдать это нельзя. Когда следствие если и не фабрикует улики, то как минимум, уводит в тень те из них, которые работают на защиту, и выставляют на первый план работающие на обвинение, причем — заметьте! — почти исключительно улики косвенные (поскольку прямые вообще бывают крайне редко). Об этом много писал еще Эрл Стенли Гарднер, добрая доля романов которого посвящены как раз ненадежности и коварству косвенных улик. В результате почти всегда для защиты необходимы неопровержимые доказательства, а для обвинения достаточно косвенных улик.

[212] В оригинале в одно слово и без запятой.

[213] Что бы сказал автор, если бы знал принцип работы современных эвристических программ: распознающих текст, антивирусных и др.

[214] В книжке — в два слова.

[215] Надо же, дело близится к концу книги, а это важнейшее понятие теории относительностей, по-моему, впервые фигурирует в нашем разговоре.

[216] Словарь дает: credibility: 1) убедительность, способность внушать доверие; надежность. 2) вера, способность поверить. Likelihood: 1) вероятность; 2) _уст. многообещающая будущность. Так что скорее всего, первое следует воспринимать как надежность, второе — как вероятность

[217] Может, и правильно, «надежность» звучала бы еще более расплывчато. А вот «сила доводово в пользу» — уже что-то смутно ощутимое.

[218] Думается, уместнее — «для него» (понятия).

[219] Как это не грустно, думается, больше 50%. Равно как и вероятность того, что миссис Джонс верна мистеру Джонсу — меньше 50%.

[220] Я, видимо, не догоняю. Имеется в виду не сама ситуация до подтверждения предположения самим фактом справедливости следствия из этого предположения, доказанной (справедливости) независимо от самого предположения»? Так только эта ситуация, по-моему, и рассматривается. Или речь идет о конкретных примерах (цифры, шарики, судебные дела, тухлые яйца и т. д.)?

[221] Значит, я правильно понял. Но до сих пор, по-моему, конкретного сравнения уверенностей в разных случаях по-моему, не проводилось… И возможно ли это? Впрочем, увидим… P{A}

[222] Наверное, этим термином, все же, обозначается вероятность (возможно, поделенная на 100, то есть, исчисляемая не в процентах, а в правильной — от 0 до 1 — дроби).

[223] И при этом, похоже, совсем перестают подкреплять друг друга, поскольку это все равно, что доказывать какое-либо утверждение, основываясь на самом этом утверждении. В этом плане вспоминается пример из первой части, кажется, когда в системе, кажется уравнений, где число уравнений равнялось числу неизвестных, и тем не менее оказалось недостаточным, поскольку два из них в разной форме выражали одно и то же и, таким образом, число уравнений оказалось на 1 меньше требуемого.

[224] Опять смутно мелькает придуманная мною история с подтасовкой улик и покупкой курева. Похоже, я прав.

[225] В книжке вычисление расположено в три строки, разделяемые знаками равенства, я здесь, возможно, и напрасно, сэкономил место. Впрочем останусь верен выбранной изначально стилистике.

[226] То есть прямое доказательство того, что часть из 875 долларов была потрачена на сигареты полностью делает ничтожной косвенную улику, поскольку рушится сам факт совпадения сумм.

[227] Вот зануда, небось целыми блоками копировал… впрочем, нет, компьетера-то у него не была. Была в лучшем случае, какая-нибудь ундервуд или эрика. Так что перепечатывал бедняга Дьердь с листа.

[228] А может, там речь шло не о рассмотренных случаях, а о предстоящем рассмотрении… Похоже, так и есть, а я действительно не догнал…

[229] Только что были несовместимы. А здесь отсылка к Пушкину Г и З несовместны. А можно даже круче предположение: Г и З несовместны, а два опровергающих предположения: Б кого-то отравил и создатель В (М) — был убийцей. Плюс к тому оба были гениями!

[230] Вот зануда! То все предлагал самим сделать необходимые вычисления, доказательства и выводы, то все разжевывает.

[231] То есть мы можем попытаться выяснить, был ли убийцей Микеланджело, травил ли кого-нибудь Бомарше, сделал ли это с Моцартом сам Сальери, не был ли злодеем сам Моцарт (масон) и наконец был ли гением Сальери.

[232] Наверное, все-таки, выражений.

[233] Наверное, по-русски лучше было бы «весомость». С другой стороны, существуют же чисто математические понятия вроде среднего взвешенного (в чем прикол, в свое время пытался понять, так и не допер).

[234] Любимая мысль Михалыча — ставки в игре должны быть максимальными. В искусстве это хорошо. Но когда речь заходит о реальной жизни, тут «кончается искусство и дышит почва (Чернобыль) и судьба (судебная «ошибка»).

[235] Неужели? Интересно, интересно…

[236] О! Похоже, сейчас будет уточнение. Ура. Наверное, можно сказать еще вероятие и правдоподобие, язык оставил резерв для смысловой нюансировки.

[237] О, а с костью еще круче, n имеет конкретное значение.

[238] Ну да, кость не может встать на вершину или ребро, и граней у нее всего 6.

[239] То есть абстрактная, у которой отсутствуют огрехи формы или неравномерность массы, а точки, отмечающие ценность грани, невесомы.

[240] Интересно, какие у него отношения с Традиционным Профессором.

[241] Да уж конечно, забудешь тут. Просто настолько в ломотину отрываться от непрерывного хода повествования и листать назад, чтобы уяснить для себя этот смысловой нюанс.

[242] Короче, протектор будет изнашиваться равномерно.

[243] Все-таки мне не нравится градация правдоподобности по степени. Да, я понимают, существуют слова малопровдоподобно (ходя ОРФО, между прочим, подчеркивает), довольно правдоподобно. Но правда всегда одна. Это сказал фараон…

[244] А здесь можно в одно слово: очевидная замена — «мало».

[245] Как в моей хохме про хрен и редьку вывод был сделан на основании невозможности «честных» образцов. Впрочем, там мое предположение подкреплялось тем, что сравнивались не две редьки или два хрена, а все-таки разные плоды, что сильно повышало его правдоподобие, правдоподобность, вероятность и т. д. и т. п. и проч.

[246] Кстати, во время предыдущей главы, когда речь шла о предположении и его следствиях, подтвержденная справедливость которых укрепляет предположение (и, мол, в естествознании это традиционный метод) у меня возник вопрос: что было предположением, а что — следствием: законы Кеплера или законы Ньютона. По времени — понятно, каков ответ. А вот по сути индуктивного рассуждения? Может, нам сейчас ответят.

[247] То есть Ньютона все же проскочили, ответ не получили…

[248] В книге использована архаическая форма написания этой фамилии с двумя «р».

[249] Меня всегда смущало число ньютоновских законов. Закон всемирного тяготения выглядел каким-то лишним. Инстинктивное ощущение гармоничности триады раздражалось. После всех стереометрических историй, рассказанных в этой книге, я понимаю, что Ньютоново законы взаимоположены не на наплоскости, образуемой триадой, а в пространстве. И тогда они образуют между собой вполне гармоничный тетраэдр. Совсем как в задачке, как из шести спичек, не ломая их, сложить четыре равносторонних треугольника.

[250] Утверждения, конечно, а не ученого.

[251] 1/6 = 0,1(6).

[252] А примеры, когда они разнятся, либо менее внятные и я их упустил, либо таковых пока не было.

[253] Придется снова листаться. Вроде бы здесь все объяснили, а — ничего не понял. Или перечитать на свежую голову.

[254] Почему же «однако»? Напротив, мы имеем не возражение высказанной мысли, а аргументацию в ее подтверждение.

[255] Замечательно точно. Не об этом же ли говорил Мачо, утверждая, что на сцене мы не можем выражать Шекспира, поскольку не знаем его замысла; выражать мы можем только себя.

[256] Видимо, редактор-марксист узрел в разговоре о «незнании» проявление агностицизма и на всякий случай дал свое не слишком внятное замечание. Подстелил, так сказать, соломки на случай, если еще кто придерется.

[257] Ну и фразочка… Речь и дет о соответствии последующей формулы представляющей собою разность между двумя вероятностями: одна вероятность для m + 1 случаев, а другая — для числа случаев, меньшего на единицу. Боюсь, изложил не менее головоломно… Как же сказать-то в простоте?!

[258] Что-то у меня в уме не получилось, проверяйте сами, если есть желание, а мне придется поверить на слово.

[259] В последующие годы было найдено несколько несходных подтверждений для очень больших величин. Впрочем доказательства так называемая бинарная проблема Гольдбаха (или проблема Эйлера) так и не получила (тернарную — для нечетных чисел — удалось доказать лишь 1997 г., имея в виду применение для этого компьютера). На июнь 2008 г. «сильная проблема» Гольдбаха (для четных чисел, о которой, собственно и идет здесь речь) была посчитана (с положительным результатом для чисел до 1,2 × 10¹⁸. Как видим, вероятность практически достигла единицы, но… ею не стала.

[260] Так Эдип отбросил опасения, решив, что вероятность убить собственного отца, а также жениться на собственной матери практически равна нулю. Но все так и случилось именно когда он отбросил опасения. Так что здравомыслящий человек не наблюдает вероятности, а говорит, что беда приходит оттуда, откуда ее не ждешь.

[261] Типичная тюремная разводка: «Ты какого года — 54-го — Спорим, нет на 1 000 000 баксов — Спорим — Гони бабки, ты 1954-го».

[262] Не понял… Если вернуться к мешку с шарами, например. При m = 0 мы вообще не вытаскиваем ни одного шара? А вероятность будет фифти-фифти? Почему чудовищно? Потому что в этом случае вообще ни о какой вероятности говорить нельзя, мы «не знаем, как устроена природа», или как там, не помню. Интересно, что сказали бы редактора́ в продолжение того своего замечания по этом поводу. Кстати, у меня в жизни был анекдот: на заводе нужно было сделать такелажный лом на ролике. Молодой инженер, исходя из своих познаний сопромата, предложил в качестве заготовки трубу, поскольку, теоретически, прочность трубы исчезающе мало отличалась от сплошного лома, но облегчала изделие и экономило материал. Старые рабочие, при этом присутствовавшие сказали, почесывая затылок: «Сломается». Инженер запальчиво заспорил, а рабочие, не отвечая, продолжали почесывать затылок. Лом был изготовлен. Он сломался.

[263] А прежде бывали. Например, Леонардо.

[264] То есть, попросту, слишком мало параметров, общих для оценки гвоздей, с одной стороны, и бубликов — с другой.

[265] В книжке в одно слова, а я уже засомневался, не дурак ли я.

[266] И что помешало?

[267] Самое интересное, что в поэтике с этим нельзя соглашаться. Ведь сама суть поэтики в сопротивопоставлении всего со всем и всему (см. Лотман Ю. М. Струкутура художественного текста)

[268] Предположения A, разумеется.

[269] (:-J

[270] Кто — «он»? Рассуждение?

[271] А что еще делать при обвинительном крене всей судебно-правоохранительной системы?

[272] В оригинале слитно.

[273] Любопытно, как биссекторы можно истолковать в плане модели «Король умирает» Ионеско. Король существует в четырех плоскостях, на каждой из которых он оказывается одновременно лишь с одним из персонажей. Те же, каждый кроме короля, оказывается на одной прямой с каждым из остальных. Львович, ты хотя бы определение прочел…

[274] Похоже, ошибка переводчика, произведение оказалось одушевленным (не изменяет кого? — произведения). Иначе согласование в предложении невозможно понять.

[275] Что-что мы имеем?..

[276] Плеоназм: «конечно» и «и подавно» — одно и то же.

[277] Так в книжке, почему-то именно эта буква не курсивом.

[278] Наверное, лучше «преобразует», «превращает».

[279]

[280] Что за чудовищное управление?

[281] Согласно грамматическим правилам, из нулей состоит квадрат, а не угол. Что за состоящий из нулей квадрат, воображение не справляется, а в пример глянуть влом.

[282] А почем средний род? А, это же утверждение, правильно, средний род.

[283] Ни хрена себе взятка! Подержанное ведро с болтами. Или это у них столько стоит бентли?

[284] Прямо Тарантино какой-то. Неужели Квен увлекался математикой? А что? Запросто!

[285] Совершенно не понятно, что имеется в виду. Но в книжке именно так — прямым фонтом и не разобрать, латиница или кириллица и вообще куда это посылают.

[286] Что-то я не нашел в книжке открывающей скобки.

[287] ~ 2/5.

[288] Больше увеличило — чудовищно. Но как сказать иначе?

[289] Помнится, когда я был в Баку (это было в 79—80-м году), меня повеселило название центрального печатного органа компартии Азербайджана. Газета называлась именно так.

[290] Что отражено на русской раскладке QWERTY-клавы: К на главном указательном, а Ы — на безыманном. Но все же не на мизинце, как ЯФЙ.

[291] Чудовищный оборот!

[292] 1-е издание, М., 1959 г.

[293] В оригинале было «remakrs» — очевидная очепятка.

[294] Фамилию автор наконец обрел свою, а имя — английская форма имени Дьердь.

---

[①] См. Д. Пойа, Как решать задачу, второе издание, М., 1961. См также книгу Д. Пойа, Математическое открытие, М., 1970. — Прим. перев.

[②] В отличие от индуктивных в более узком смысле слова, автор называет их «правдоподобными» — plausible — рассуждениями.

[③] Предисловие С. А. Яновской написано в 1957 г. — Прим. перев

[④] Их можно рассматривать, например, как модальности. (Модальности типов «необходимо», «возможно» и др. ввел, как известно, в рассмотрение еще Аристотель. В настоящее время им посвящена в логике большая литература. См., например, книгу von Wight G. H., An Essay in Modal Logic, 1951.)

[⑤] На стр. 366 (и соседних) автор приводит ряд примеров, свидетельствующих о том, каким нелепым (и даже противоречивым) выводам может приводить иногда приписывание правдоподобностям числовых значений. О теории вероятностей как о теории правдоподобностей, образующих частично упорядоченную систему, см., например, в книге Г. Биркгофа, Теория структур, М., 1952, стр. 275, где имеются ссылки и на другую литературу.

[⑥] В действительности и в доказательной логике мы не обходимся без предположений. Мы предполагаем, например, что индивидуальные объекты, к которым относятся наши рассуждения, остаются строго неизменными, пока мы рассуждаем о них; что любые два высказывания, сколь длинными они ни были бы, всегда можно объединить — например с помощью союзов «и», «или»¸ «если… то» — в новое высказывание; что в таких-то наших рассуждениях можно свободно пользоваться законом исключенного третьего и т. п. Из этого не следует, однако, будто все наши знания состоят только из предположений. Ведь даже во всякой относительной истине всегда имеется момент абсолютной истины. И чем иным может быть надежное предположение, как не оправдывающимся на практике, т. е. в конечном счете ведущим к истине. — Прим. ред.

[⑦] В русском издании оба тома объединены в одной книге. — Прим. перев.

[⑧] Д. Пойа. Как решать задачу. Все ссылки в дальнейшем делаются на 2-е издание этой книги, М., 1961.

[⑨] Исследовательская работа в этом направлении была предпринята в отделении психологии Стэнфордского университета в рамках проекта, руководимого Э. Р. Хильгардом и субсидируемого Научно-исследовательским управлением ВМС США.

[⑩] Euler, Specimen de usu observationum in mathesi pura, Opera Omnia, ser. 1, vol. 2. p. 459.

[⑪] Euler, Opera Omnia, ser, 1, vol. 2, p. 1—5. Hardy G. H. and Wright E. M., An Introduction to the Theory of Numbers, p. 14—15.

(См. также Л. Эйлер, Письма к ученым, М. — Л., 1963, стр. 283—285. — Прим. перев.)

[⑫] В оригинале «a burnt child dreads the fire — Прим. перев.»

[⑬] Этот параграф с небольшими изменениями воспроизводит заметку автора в Amer. Math. Monthly, 55 (1948)? 241—243.

[⑭] Более 30 лет своей жизни Эйлер провел в России, где опубликовал в изданиях Петербургской Академии наук, членом которой он являлся, бо́льшую часть своих работ. — Прим. перев.

[⑮] Значительно позже, почти через десять лет после своего первого открытия, Эйлер возвратился к этому вопросу, ответил на возражения, до некоторой степени завершил свой первоначальный эвристический подход и дал новое, существенно иное доказательство. См. Euler, Opera Omnia, ser. 1, vol, 14, p. 73—86, 138—155, 177—186, также 156—176, где содержится заметка Пауля Штеккеля об истории этой задачи. (См. также Л. Эйлер, Письма к ученым, М. — Л. 1963, стр. 179—193, 212—215, 227—228. — Прим. перев.).

[⑯] В § 6 (3), (4), (5). Собственное краткое изложение Эйлера см. в Opera Omnia, ser. 1, vol. 14, p. 140.

[⑰] Представления sin x в виде бесконечного произведения.

[⑱] Особенно произведение для 1— sin x.

[⑲] На самом деле под «точной теорией» обычно понимается теория, которая может быть арифметизирована так, что теоремы этой теории превращаются в теоремы арифметики. Объявление предметом математики любых объектов «которые могут быть объектами точной теории», таким образом, не выводит на свмом деле за пределы энгельсовского определения математики как науки о количественных отношениях и пространственных формах действительного мира (см. Энгельс Ф., Анти-Дюринг, стр. 37, Госполитиздат, 1953; БСЭ, II изд., статья «Математика»). — Прим. ред.

[⑳] См. Sir Isaas Newton’s Mathematical Principles of Natural Philosophy and his System of the World, Berkeley, 1946, p. 551. [В русских изданиях Начал Ньютона перевод работы «The system of the World» (Система мира) отсутствует. — Прим. перев.

[21] Полиа Г. и Сеге Г., Задачи и теоремы из анализа, М., 1956, т. 1, стр. 12.

[22] Лаплас, Опыт философии теории вероятностей, М., 1908, стр. 7.

[23] Gauss, Werke, Vol. 2, S. 3.

[24] Части этой главы уже были напечатаны под заглавием «Let us teach guessing» («Научимся догадываться») в книге Études de philosophie des sciences en hommage à Ferdinand Gonseth, éditions du Griffon, 1950, p. 147—154.

[25] Речь идет о профессоре математики — традиционном персонаже анекдотов о математиках; см. «Как решать задачу», стр. 98. — Прим. перев.

[26] Приведенному изречению этого хорошо известного педагога иногда предшествует следующее увещание: «Если вы должны доказать теорему, не торопитесь. Прежде всего полностью поймите, что теорема говорит, попытайтесь ясно увидеть, что она означает. Затем проконтролируйте теорему, она может оказаться неверной. Рассмотрите ее следствия, проверьте столько частных примеров, сколько нужно, чтобы убедить вас, что она верна. Когда …»

[27] Ср. Putnam, 1949.

[28] См. Putnam, 1948.

[29] См, например, Харди Г. Х., Курс чистой математики. М., 1949, § 82. (Число l называется верхним пределом последовательности x_n, если для любых чисел p и q таких, что p > l > q, найдется бесконечное множество номеров n, для которых x_n > p, и лишь конечное число номеров n, для которых x_n > q. — Прим. перев.)

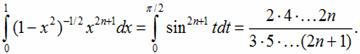
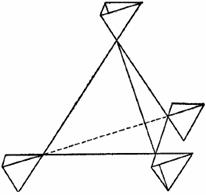
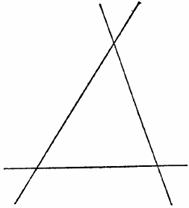
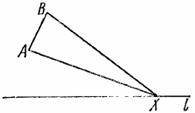
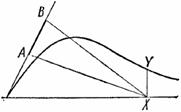
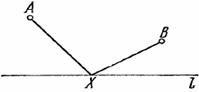
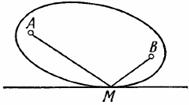
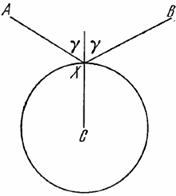
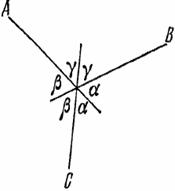
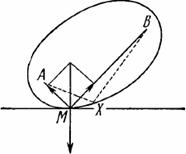
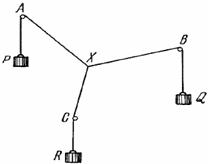
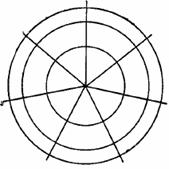
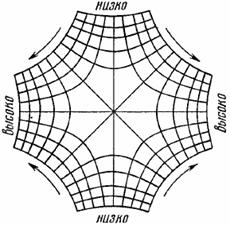
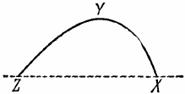
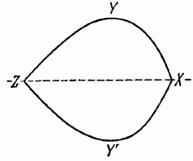
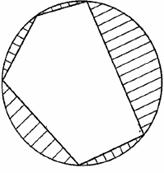
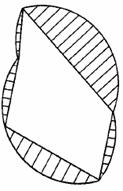
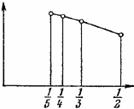
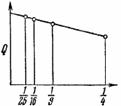
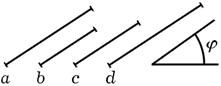
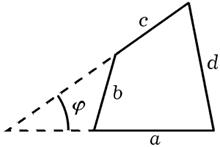
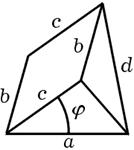
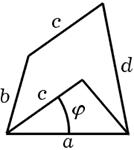
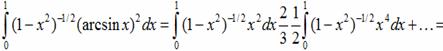
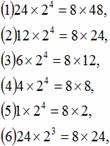
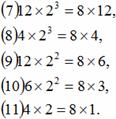
[30] Так, например, первому «дереву» соответствует структурная формула (бутиловый спирт). — Прим. перев.

[31] В полном объеме. — Прим. перев.

[32] Оригинал на французском языке; см.: Euler, Opera Omnia, ser. 1, vol. 2, p. 241—253. Изменения состоят в перемене обозначения (примечание на стр. 112), в другом устройстве таблицы (объясненном в примечании на стр. 113), в незначительных изменениях, относящихся к нескольким формулам, и в том, что в последнем п. 13 статьи опущено повторение предшествующих рассуждений. Читатель может свериться с легко доступным оригиналом.

[33] Эйлер первым ввел символ для суммы делителей. Он пользовался символом ∫n, а не современным σ (n), принятым в тексте.

[34] Число, стоящее в пересечении строки с отметкой 60 и столбца с отметкой 7, т. е. 68, есть σ (67). Если p простое, то σ (p) напечатано жирным шрифтом. Таблица устроена несколько более сжато, чем в оригинале.

[35] Этот очерк впервые был опубликован в моей статье «Heuristic Reasoning and the Theory of Probability», Amer. Math. Monthly, 48 (1941), 450—465. Курсив в очерке указывает фразы, не принадлежащие Эйлеру.

[36] Opera Omnia, ser. 1, vol 4, p. 125—135.

[37] См. также для дальнейших ссылок книгу Hardy G. H., Wright E. M., An Introduction to the Theory of Numbers, Oxford, 1938, ch XX.

[38] Мах Э. Познание и заблуждение, М., 1909, стр. 316. [Смысл этой довольно туманной фразы (под «членом понятия» здесь, очевидно, имеется в виду элемент его объема) автор пытается объяснить в тексте главы. Нам, однако, представляются, что, собственно, к математической индукции она имеет малое отношение: ведь с помощью метода математической индукции доказываются не свойства понятия числа, а свойства чисел. Так, если B есть понятие натурального числа, а C₁, C₂, … C_n, … — натуральные числа 1, 2, …, n, …, то в доказательствах с помощью математической индукции доказывается не A (B) (где A (B) означает, что B обладает свойством A), а истинность A(n) для всякого n — Прим. ред.]

[39] См. «Как решать задачу», стр. 95.

[40] Мах был уверен, что метод математической индукции изобрел Яков Бернулли, но, по-видимому, наибольший вклад в его изобретение принадлежит Паскалю. Ср. Freudenthal H., Archives internationales d’histoire des sciences, no. 22 (1953), p, 17—37. Ср. также Jacobi Bernoulli Basileensis Opera, vol. 1, Genève, 1744, p. 282—283.[В истории открытия метода математической индукции, на мой взгляд, недостаточное место уделяется Декарту. Суть его знаменитого правила Энумерации ведь и состояла в том, что для изучения необозримого множества случаев их необходимо расположить «как бы по ступеням» (упорядочить по типу натурального ряда чисел), изучить свойства объекта, находящегося на первой ступени, и способ перехода от одной ступени к следующей. Так именно Декарт и считал возможным изучить общие свойства алгебраических кривых. — Прим. ред.]

[41] Роль перехода от n к n + 1 в доказательствах с помощью математической индукции вряд ли действительно простою ссылкою на необходимость изучать инварианты изменения.

Здесь, скорее, следовало бы отметить, что с помощью математической индукции доказательство общего предложения о свойстве всех натуральных чисел сводится (после того как уже проверено, что единица обладает этим свойством) к доказательству другого, общего же, но обычно более легкого для доказательства предложения о «наследуемости» рассматриваемого свойства в ряду натуральных чисел (переход от n к n + 1). Если доказательству подлежит категорическое утверждение, что «всякое число n обладает свойством S», — запишем это в виде (n)S(n)(«для всякого n верно, что n обладает свойством S», — то таким мы сводим доказательство его к: (а) доказательству условного предложения: «для всякого n верно, что если n обладает свойством S, то и n + 1 также обладает свойством S» [(n) (S(n)→S(n + 1))], и (б) доказательству частного предложения: «единица обладает свойством S» [S,(1)]. Заметим, что если каждое из двух высказывания A и B имеет одинаковые шансы оказаться истинным или оказаться ложным, то шансы каждого из них на ложность равны ½. Импликация же A→B может быть ложна только в случае, когда A истинно, а B ложно, т. е. ее шансы на ложность равны ¼. Пользуясь терминологией автора, можно было бы сказать поэтому, что условное предложение: (n) [S(n) → S(n + 1)] более правдоподобно, чем категорическое: (n)S(n). Несмотря на бо́льшую громоздкость выражения условного предложения, довольно естественно ожидать поэтому, что доказать его легче, чем доказать категорическое. Важность общности этого условного предложения (требования, чтобы оно было верно для совершенно произвольного n) хорошо видна на примера 17 и 18. — Прим. ред.

[42] Это «парадокс изобретателя»; см. «Как решать задачу», стр. 138.

[43] См.: Эйлер Л., Метод нахождения кривых линий, обладающих свойствами максимума либо минимума, или Решение изопериметрической задачи, М. — Л., 1934, стр. 447.

[Однако уже Вольтер возражал, что богу необязательно быть бережливым буржуа, он может хотеть и чтобы его считали щедрым аристократом, не жалеющим средств на усовершенствование мира. — Прим. ред.]

[44] Если мы рассмотрим ∠ AXB как функцию расстояния, измеряемого вдоль прямой l то сможем обычным способом нарисовать ее график (изобразить его в прямоугольных координатах). Рис. 8.2 дает качественный набросок графика; ∠AXB изображается ординатой XY.

[45] Очень легко, если мы посмотрим на рис. 8.2.

[46] Функция нескольких переменных, непрерывная на ограниченном замкнутом множестве, достигает своей верхней и нижней грани. Это обобщает теорему 2 в книге Харди Г. Х., Курс чистой математики, стр. 192.

[47] Pappus, Collectiones, 5.

[48] Simon Lhuillier, Poligonométrie et Abrégé d’Isopérimétrie élémentaire, Genève, 1789. Steiner J., Gesammelte Werke, Vol. 2, р. 177 — 308.

[49] Пуанкаре А., Ценность науки, М., 1906, стр. 108.

[50] Ср. The Method of Archimedes, edited by Thomas L. Heath (Метод Архимеда, изданный Томасом Л. Хитом), Cambridge, 1912, p. 13. (См. также: Архимед, Сочинения, М, 1962, стр. 298—327, Послание к Эратосфену. Особенно см. стр. 302—304. Ниже эта книга цитируется как Метод. — Прим. перев.)

[51] См. Метод, стр. 299.

[52] Я несколько раз излагал этот вывод формулы объема шара в моих классах и однажды заслужил комплимент, которым я горжусь. После моего обычного: «Есть ли какие-нибудь вопросы?» в конце вывода один юноша спросил: «Кто заплатил Архимеду за его открытие?» Должен признаться, я не был достаточно находчив, чтобы ответить: «В те дни такие исследования поддерживала только Урания, муза науки».

[53] Метод, стр. 302.

[54] Метод, стр. 299.

[55] В оригинале «Not so deep as a well». — Прим. перев.

[56] Для других замечаний об открытии Архимеда см.: van der Wærden B. L., Elemente der Mathematik, v. 8, 1953, р. 121—129; v. 9, 1954, р. 1—9.

[57] Комментарии к определениям XV и XVI первой книги Начал Евклида.

[58] Convivio (Пир) II, ХIII, 26.

[59] Рене Декарт, Избранные произведения, М., 1950, стр. 104. Место несущественно изменено; рассматриваемое свойство круга дано здесь в иной форме.

[60] Объяснение этого названия и эквивалентные формы будут даны позднее (§ 8).

[61] Лучше осведомленный кот должен был бы делать минимальной не поверхность своего тела, а его теплопроводность или, что сводится к тому же, его электростатическую емкость. Однако в силу одной теоремы Пуанкаре эта другая задача на минимум имеет то же решение, шар. См. Pólya G., Amer. Math. Monthly, 54 (1947), 201—206.

[62] См. Рэлей, Теория звука, М., 1955, т. 1, стр. З65.

[63] См. §§ 12.4 и 12.5. — Прим. перев.

[64] Теоремы и доказательства этого параграфа принадлежат Люильеру, см. примечание на стр. 157.

[65] Записывая вместо «изопериметрическое частное» сокращенно И. Ч., мы могли бы сказать, что круг имеет наибольшее И. Ч.

[66] Мы рассматриваем здесь только замкнутые поверхности «топологического типа» сферы и исключаем, например, (баранкообразный) тор.

[67] Доказательства указанных и аналогичных теорем см. в книге Г. Полиа и Г. Сеге, Изопериметрические неравенства в математической физике, М., 1962.

[68] Харди Г. Г., Литтлвуд Дж. Е. и Полиа Г., Неравенства, М., 1948, стр. 133 — 135 и цитированные там теоремы.

[69] Сравнение не доказательство (франц.). — Прим. перев.

[70] Лаплас, Опыт философии теории вероятностей, М., 1908, стр. 187.

[71] «Как решать задачу», стр. 202.

[72] См. Галилео Галилей, Избранные труды, М., 1994, т. 2, стр. 238—246.

[73] В этом и в следующем параграфе, а также иногда и в других местах книги мы переводим словом фон английское слово background. Автор имеет в виду совокупность неосознанных мыслей и представлений человека, его опыт и знания, быть может, и в неокончательно оформленном виде, влияние окружающей его среды и мировоззрения, так сказать, весь его «умственный багаж». — Прим. перев.

[74] Кеплер отвергает объяснение Ретикуса: существует шесть планет, так как 6 является первым «совершенным числом».

[75] «Как решать задачу», стр. 200 — 201.

[76] См. Харди Г. Х., Курс чистой математики, М., 1949, стр. 503—505.

[77] Ср. Whewell W. The Philosophy of the Inductive Sciences.new ed., v. 1, р. 146.

[78] См. Schwarz H. A., Gesammelte Mathematische Abhandlungen, V. 2, S. 309 — 311. (См. также Фихтенгольц Г. М., Основы математического анализа, т. 2, п. 364. — Прим. перев.)

[79] См. примечание на стр. 212. — Прим. перев.

[80] Английское слово «pattern» (образец, образчик, форма, шаблон) мы переводим словом «схема», поскольку речь идет об обобщении накопленных наблюдений, имеющем вид общей рекомендации — правила, которому для легкости запоминания придается вид некоторой схемы. — Прим. ред.

[81] Russell B. Philosophy, W. W. Norton and Co., 1927, p. 80.

[82] Части этой главы были использованы в моей речи «On plausible reasoning», опубликованной в Proc. Intern. Congr. Math. Май». 1980, v. 1, p. 739 — 747.

[83] Opera Omnia, ser. 1, vol. 4, p. 12) — 124. В этом контексте Эйлер рассматривает 1 как простое число; это необходимо для счета в случае 3 = 1+ 2 × 1.

[84] Сообщеняе профессора Лемера (D. H. Lehmer).

[85] См. примечание к названию главы (стр. 229). — Прим. ред.

[86] Opera Omnia, ser. 1, vol. 16, sect. 1, p. 241— 265.

[87] См. статью автора: Sopra una equazoine transcendente tratta da Eulero, Bolletino dell’ Unione Matematica Italiana, 5 (1926), 64—68.

[88] См. статью автора: Remarks on power series, Acta Scientiarum Mathematicarum, 12В (1950), 199—213.

[89] См. примечание на стр. 212. — Прим. перев.

[90] Одиннадцатое из его правил для руководства ума. См. Рене Декарт, Избранные произведения, М., 1950, стр. 117.

[91] Мы излагаем здесь формальную логику на «старомодный» манер (пользуясь обычным языком и избегая логических символов, насколько это осуществимо), но с несколькими современными идеями. Некоторые из простейших логических символов будут несущественно использованы позднее, особеню в § 7.

[92] См. Риман Б., Сочинения. М.— Л., 1948, стр. 218—219. — Прим. перев.

[93] Трудности, связанные с применением закона исключенного третьего к бесконечным множествам, заставляют иногда отказываться от признания правильности этой эквивалентности. Из утверждения, что «A истинно», и без закона исключенного третьего можно заключить, что «не-A ложно», обратное же не всегда возможно. — Прим. ред.

[94] Трудности, связанные с применением закона исключенного третьего к бесконечным множествам, заставляют иногда отказываться от признания правильности этой эквивалентности. Из утверждения, что «A истинно», и без закона исключенного третьего можно заключить, что «не-A ложно», обратное же не всегда возможно. — Прим. ред.

[95] Если несовместность A с B понимать только в том смысле, что по крайней мере одно из двух высказываний A и B ложно, то слово «следует» («имплицирует») в этом абзаце в точности соответствует употребляемой обычно в математической логике импликации (которую нужно отличать от — более близких к аристотелеву пониманию алогического следствия» — разновидностей «строгой» или «сильной» импликации). Как явствует, однако, из остального контекста, авторское «следует» («имплицирует») не совпадает с обычной импликацией (которую мы здесь будем обозначать знаком ⊃). Ведь если B истинно, то A ⊃ B («A имплицирует B») истинно, каково бы ни было A, так что делать какие-нибудь заключения насчет A в случае одновременной истиннасги B и A ⊃ B заведомо нельзя. Между тем автор полагает, что в этом случае можно заключить, что A более правдоподобно (фундаментальная индуктивная схема). (Аналогичные замечания относятся к случаю, когда B ложно, а B ⊃ A истинно, а также к авторскому пониманию несовместности, см., например, табл. 1, стр 253.) Аксиоматическое определение употребляемых авторам понятий «следует» «более правдоподобно» и др. нетрудно получить, очевидно, обозревая рассматриваемые им схемы, но его интересы концентрируются на обосновании этих схем с помощью интерпретации их для правдоподобностей, о чем см. особенно гл. XV. Здесь заметим еще только, что в отличие от обычное импликации: A ⊃ B, истинность или ложность которой определяется только истинностью или ложностью каждого из высказываний A и B, в фундаментальной индуктивной схеме автора на самом деле предполагается, что A и B каким-то образом связаны между собой, например B без A «мало правдоподобно» и т.п. (см. §§ 10, 13). В настоящее время существует большая литература по логике модальностей, строгой импликации и других связей, аналогичных рассматриваемым Пойа. — Прим. рад.

[96] Опять в предположении верности закона исключенного третьего или, точнее, эквивалентности двойного отрицания A утверждению A. — Прим. ред.

[97] Напомним, что и в случае отказа от закона исключенного третьего верно, что из A следует двойное отрицание A. — Прим. ред.

[98] При отказе от закона исключенного третьего эта эквивалентность в общем случае не будет иметь места: из левой ее части правая всегда будет следовать, из правой же всегда можно будет заключить, что «из двойного отрицания A следует двойное отрицание B». Если A и B — отрицательные высказывания, то рассматриваемая эквивалентность верна для них и в конструктивной логике (без закона исключенного третьего). — Прим. ред.

[99] В классической формальной логике. — Прим. ред.

[100] В классической формальной логике. — Прим. ред.

[101]

[102] Гильберт Д. и Аккерман В., Основы теоретической логики, М., 1947.

[103] См. примечание 1 на стр. 248. — Прим. ред.

[104] См. примечание 1 на стр. 248. — Прим. ред.

[105] См. примечание 1 на стр. 248. — Прим. ред.

[106] См. примечание 1 на стр. 248. — Прим. ред.

[107] См. примечание 1 на стр. 248. — Прим. ред.

[108] Так, изопериметрическая теорема и гипотеза Рэлея, которые мы сравнили в § 12.4, могут подсказать идею их совместного обобщения.

[109] Ср. Wigmore J. H. The principles of judicial proof, Boston, 1913, p. 9—12, 15—17.

[110] Относительно следующего случая читателю следует справиться в решениях Верховного суда штата Иллинойс, почти полностью перепечатанных у Уигмора; см. цитированную в примечании на стр. 260 книгу.

[111] Ср. книгу Уигмора, цитированную на стр. 260.

[112] The Manchester Guardian Weekly, November 29, 1951. «Пример, естественно, пришлось заменить; соответственно были немного изменены и наводящие вопросы. В оригинале имеется в виду слово «Tiredness» — усталость. — Прим. перев.)

[113] Ср. Maxwell J. C., A treatese on electricity and magnetism, 2 ed., 1881, vol. 1, p 76—82.

[114] Между прочим, эксперимент Кавендиша имел даже более широкую цель: он стремился показать, что закон r^–2 более приемлем, чем любой другой закон φ(r) без ограничения, что функция φ(r) имеет вид r^–α; см. Максвелл, там же, стр. 76—82.

[115] Я не изобретаю гипотез (лат.). — Прим. перев.

[116] Т. е. физикой. По-английски philosophy — философия, natural philosophy — физика. — Прим. перев.

[117] Статьи автора этой книги цитируются в втой сноске без указания фамилии; указываются страницы, на которых (иногда в форме вопроса) высказано предположение; статья, цитированная с фамилией, указывает первое доказательство рассматриваемого предположения. Пример 12: Rendiconti Circolo Matematico di Palermo, 34 (1912), 69 — 120. Пример 13: °L’Intrmédiaire des Mathéaticiens°, 21 (1914), 27, quest. 4340; Szegö G., Math, Annalen, 76 (1915), 490—503. Пример 14: Math, Annalen, 77 (!1916), 497—513; ср. 510; Carlson F., Math. Zeits., 9 (1921), 1—13. Пример 15: L’Intermédiaire des Mathéaticiens, 20 (1913), 145—146, quest. 4240; Szegö G., Math. Zeits., 13 91922), 38; см. также Journal für die reine und angewandte Math., 158 (1927), 6—18. Пример 16: Jahresberichte der Deutschen Math. Vereinigung, 28 (1919), 31—40; ср. 36. Пример 17: Proceedings of the National Academy of Sciences, 33 (1947), 218—221; ср. 219. Пример 19: Journal für die reine und angewandte Math., 151 (1921), 1—31; см. теорему 1, стр. 3.

[118] Ср. Полиа Г. и Сеге Г., Задачи и теоремы из анализа, М., 1956, т. 1, стр. 11.

[119] То есть они «задают тон» (нем.). — Прим. перев.

[120] Теорема Фабри утверждает, что степенной ряд не может быть продолжен за круг его сходимости. Литературные ссылки см. в Encykl. Der Math Wiss., II C4, S, 460—463. — Прим. перев.

[121] Ср. Ж. Адамар, Исследование психологии процесса изобретения в области математики, М., 1970, стр. 81—82.

[122] Abhandlungen der K. Akademie der Wissenschaften, Berlin, 1861, 78—80.

[123] Раньше слова «вероятно» и «вероятность» иногда употреблялись в нетехническом смысле, но в настоящей главе и в следующей мы будем этого старательно избегать. Слова «правдоподобно» и «правдоподобие» будут введены как технические термины в этой главе позже.

[124] В этом существенном пункте и в нескольких других настоящее изложение следует взглядам Р. Мизеса, хотя оно отклоняется от его определения математической вероятности; ср. его книгу «Вероятность и статистика», М., 1930.

[125] В азартные игры люди играли еще в античной древности. Но азартные игры были использованы для создания теории вероятностей, только когда появилась потребность в общей теории некоторых массовыхслучайных явлений и убеждение в том, что такая теория вообще возможна. — Прим. ред.

[126] См. Мах Э., Механика, СПб., 1909, стр. 59—61.

[127] В той мере, в какой ее «несомненность» могла бы препятствовать дальнейшему развитию науки. Однако во всякой подлинно научной теории есть элемент несомненной, абсолютной истины. Иначе она не имела бы права претендовать на «подлинную научность». — Прим. ред.

[128] См. примечание на стр. 286. — Прим. ред.

[129] Philosophical Magazine, ser. 5, 50 (1900)? 167—169; статья Карла Пирсона.

[130] Корренсом; см. Johannsen W., Elemente der exakten Erblichkeitslehre, Jena, 1909, S. 371.

[131] Bertrand J., Calcul des probabilités, VII—VIII.

[132] Буквально «Кровь Вакха» (итал.) — ругательство. — Прим. перев.

[133] По поводу определения Мизеса см. статью А. Я. Хинчина: «Учение Мизеса о вероятностях и принципы физической статистики», УФН, 9, вып. 2 (1929), 141—166. — Прим. перев.

[134] Как известно, США имеется 50 штатов. — Прим. перев.

[135] Мы следуем А. Пуанкаре; см. Poincaré H., Calcul des probabilités, p. 35—39.

[136] Маленькое словечко «или имеет два значения, которые недостаточно различаются английским языком и другими современными европейскими языками. (Они, однако, до некоторой степени различаются в латинском языке.) Мы можем пользоваться «или» «исключающе» или «включающе». «Вы можете пойти на пляж или в кино (не туда и туда сразу), — здесь исключающее «или» (в латинском «aut»). Вы можете пойти на пляж или купить много конфет», — здесь включающее «или», если вы имеете в виду то или другое или и то, и другое». В юридических или финансовых документах включающее «или» передается как «и/или» (в латинском «vel»). В P{A или B} мы имеем в виду включающее «или».

[137] Лаплас, Опыт философии теории вероятностей. М., 1908, стр. 187.

[138] Keynes J. M., A treatise on probability, p. 259.

[139] См. примечание на стр. 212. — Прим. перев.

[140] Аристотель, Аналитики первая и вторая. М., 1952, стр. 10. — Прим. перев.

[141] Мы переводим английское слово credibility словом правдоподобность а слово likelihood — словом правдоподобие. — Прим. перев.

[142] То, что исчисление вероятностей в первую очередь должно было бы иметь дело со степенями веры (доверия, подтверждения, уверенности, …), а не с более или менее идеализированными относительными частотами, является мнением многих авторов, из которых я приведу только двух: Д. М. Кейнса [A treatise on probability (см. особенно стр. 34, 66, 160)] и Б. де Финетти (La Prévision, ses lois logiques, ses sources subjectives, Annales de l’Institut Henri Poincaré, 7 (1937), p. 1—68). Здесь не место объяснять мои отличия от этих авторов или различия между ними, но я хочу выразить благодарность им обоим. Точка зрения, принятая здесь, сходна с точкой зрения моей более ранней статьи «Heuristic reasoning and the theory of probability». Amer. Math. Monthly, 48 (1941), 450—465, но не полностью с ней совпадает.

[143] См. примечание на стр. 347. — Прим. перев.

[144] Это обычная ситуация. Только в исключительных случаях статистик в состоянии приписать P{С} числовое значение.

[145] Но речь идет именно о раскрытии «внутреннего механизма» природы всеми доступными естествоиспытателю средствами, в том числе и с помощью наблюдений. — Прим. ред.

[146] Лаплас, Опыт философии теории вероятностей, М., 1908, стр. 23.

[147] Это несколько отличается от обычной терминологии. Ср. Keynes J. M., A treatise on probability, p. 372—383.

[148] Лаплас, Опыт философии теории вероятностей, М., 1908, стр. 23, 24.

[149] Приписывание правдоподобности числового анализа на основании какого-либо допущения о взаимозаменяемости или симметрии (что мы делали в примере 4) следует здесь рассматривать как тривиальное: чтобы оправдать количественные правдоподобности требуется что-то большее и более новое.

[150] Как уже было отмечено, автор предполагает применимость во всех условиях одних и тех же правил доказательной формальной логики. — Прим. ред.

[151] Смысл суда присяжных состоит, конечно, не во внесении субъективного элемента в объективные правила, а в том, чтобы сделать решение суда наивозможно более беспристрастным, т. е. объективным. В соотношении между формальной правильностью (которую у автора здесь обеспечивает судья) и содержательной истинностью (присяжные) ведущая роль должна принадлежать содержательной истинности, критерием которой служит практика: кто же согласится принять такие формальные правила умозаключения, с помощью которых из содержательно истинных посылок можно вывести не оправдывающиеся на практике заключения! — Прим. ред.

[152] Oeuvres de Descartes, ed. Adam et Tannery, vol. 10, 1908, p. 204.

[153] Параграфы 4, 5 и 6 с незначительными изменениями воспроизводят части моей статьи «With, or without motivation?», Amer. Math. Monthly, 56 (1949), 684–691.

[154] Дословно: бог из машины (лат.). Это выражение, употребляемое в ироническом смысле, означает неожиданно в самый нужный момент пришедшую помощь, вмешательство свыше. В античном театре боги появлялись на сцене с помощью специальной машины. — Прим. перев.

[155] Меня можно извинить за то, что я выбрал пример из моей собственной работы. См. G. Pólya, Proof of an inequality, Proc. Lond. Math. Soc. (2), 24 (1925), 57. Доказанная теорема принадлежит Т. Карлеману.

[156] По поводу этой терминологии см. «Как решать задачу», стр. 83.

[157] Ср. «Как решать задачу», стр. 20-2—203.

[158] См. примечание на стр. 212. — Прим. перев.

[159] Изложение, промежуточное между § 4 и § 6, см. в книге Харди Г. Г. , Литлвуд Дж. И. и Полиа Д., Неравенства, М., 1948, стр. 299–301.

[160] Муж английской королевы принадлежит к семье английских пэров, сменившей в 1917 г. свою немецкую фамилию Баттенберг на Маунтбэттен. — Прим. перев.

[161] См. G. Pólya, Sur les types des propositions composées, Journal of Symbolic Logic, 5 (1940), 98–103.

[162] Значение интуиции и её роль в группировке деталей обычно не слишком хорошо объясняются. Замечательно, однако, что Декарт, от которого ведёт происхождение современное употребление термина «интуиция», оба эти момента объясняет довольно убедительно, в третьем и седьмом из своих правил для руководства ума. См. Рене Декарт, Избранные произведения, М., 1950, стр. 84—88 и 101—105.

[163] См. примечание на стр. 212. — Прим. перев.

[164] В_р — вершина разбиения (соответствует букве В в обозначениях гл. III). — Прим. перев.

[165] В предположении, что рассматриваемые интегралы сходятся. — Прим. перев.

[166] Если имеется в виду вероятность того, что хотя бы трое часов из четырех находятся в «согласии, то в приведенное выражение нужно внести поправку, которая, впрочем, составляет всего – 0, 0000002. — Прим. перев.

[167] Так как не при всяких a, b и c число d окажется целым, то благоприятствующих случаев в (II) будет меньше, чем 2n(2n + 1)², и искомая вероятность будет больше написанного ниже числа. И во всяком случае она будет больше, чем — Прим. перев.

[168] См. также книги серии «Библиотека математического кружка». — Прим. перев.

[169] См. также Д. Пойа, Математическое открытие, М., 1970. — Прим. перев.